
1119
.pdfПример 1.7. Запишите индексы Миллера для плоскости, содержащей узлы с индексами [[100]], [[020]], [[004]], примитивной кубической решетки.
Решение
Используя аналитический метод, найдем уравнение плоскости, проходящей через заданные узлы. Уравнение плоскости, проходящей через три
точки, дается определителем 3-го порядка: |
|
|
|
8 − 1 ; < |
||||
8 − 1 |
; − 0 |
< − 0 |
|
или |
|
> |
||
>0 − 1 |
2 − 0 |
0 − 0> = 0 |
|
|
−1 2 0> = 0. |
|||
0 − 1 |
0 − 0 |
4 − 0 |
|
|
|
|
|
−1 0 4 |
Разложим определитель по элементам первой строки: |
|
|||||||
|
|
(8 − 1) @2 |
0@ − ; @−1 |
0@ + < @−1 |
2@ = 0. |
|||
|
|
0 |
4 |
−1 |
4 |
−1 |
0 |
|
Раскрывая определители 2-го порядка, получим |
|
|
||||||
|
88 − 8 + 4; + 2< = 0 |
или |
48 + 2; + < = 4. |
|||||
Коэффициенты при x, y, z и есть индексы плоскости, следовательно, индексы Миллера для плоскости (421).
Самостоятельно убедитесь в том, что результат будет тот же, если
известны |
отрезки, отсекаемые плоскостью на осях координат |
(кристаллографические направления). |
|
|
Ответ: (421). |
Пример 1.8. Напишите индексы направления прямой, проходящей через |
|
узлы [[77 |
]] и [[707]]. |
121 |
2 1 |
Решение
Запишем уравнение прямой, проходящей через две точки: |
|||
8 − :+ |
; − + |
< − =+ |
|
: − :+ = − + = = − =+. |
|||
Подставим заданные индексы узлов: |
< − 1 |
||
8 − (−1) |
; − |
(−2) |
|
−2 − (−1) = 0 − |
(−2) |
= −1 − 1 |
|
|
11 |
|
|
или |
8 + 1 |
= |
; + 2 |
= |
< − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
−1 |
2 |
−2 . |
|
|
|
|
|
|
||
Величины, стоящие в знаменателе, являются индексами направления. |
|||||||||||
Таким образом, индексы прямой [72 |
7]. |
|
|
Ответ: [ |
7 |
2 |
7 |
]. |
|||
|
|
1 |
2 |
|
|
|
|
|
|
||
Пример 1.9. Нормаль к некоторой плоскости в |
z |
1 2 |
|
||||||||
|
|
|
|
||||||||
кубической решетке задана индексами [110]. |
|
|
|
|
|
|
|||||
Определите индексы Миллера этой плоскости и |
|
|
|
|
|
|
|||||
наименьшие отрезки, отсекаемые плоскостью на |
|
|
|
|
|
|
|||||
кристаллографических осях. |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Индексы для плоскости совпадают с индексами |
|
|
|
|
|
|
|||||
x |
|
|
|
|
|||||||
направления нормали к |
этой |
плоскости |
[110]. |
|
|
[100] |
|||||
Плоскость с такими индексами показана на рис. 5 |
|
|
|
|
|||||||
Рис. 5. |
|
|
|
|
|||||||
(заштрихованная область). |
Положение |
плоскости |
|
|
|
|
|||||
|
|
|
|
|
|
||||||
определяется заданием трех отрезков a, b, c, которые
она отсекает на осях решетки. Индексы такой плоскости отыскиваются
следующим образом. Выражают отрезки a, b, c |
в осевых единицах и |
||||
записывают величины, обратные этим отрезкам: A+ ; C+ ; |
|
+DE. По условию задачи |
|||
1 |
= 1; |
1 |
1 |
|
= 0. |
|
F = 1; |
|
|
||
|
=> = 1, F = 1, |
= ∞. |
|
||
Это и есть наименьшие отрезки, отсекаемые плоскостью на кристаллографических осях.
Ответ: индексы плоскости [110], наименьшие отрезки a = 1, b = 1, c = ∞.
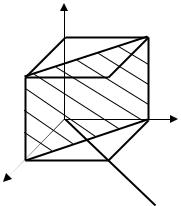
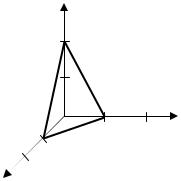
Пример 1.10. Система плоскостей в примитивной кубической решетке задана индексами (221). Найдите наименьшие отрезки, отсекаемые плоскостью на осях координат, и изобразите эту плоскость графически.
Решение
Графическое изображение плоскости представлено на рис. 6.
12
Для нахождения отрезков, запишем
величины, обратные индексам, т.е.
1 1 1.
2 2 1
После приведения этих дробей к общему |
|
|||
знаменателю, |
отбросим его и отрезки a, b, и c |
|
||
1 |
1 |
1 |
· 2 = 2. |
|
= 2 · 2 = 1; F = 2 |
· 2 = 1; = 1 |
x |
||
|
|
|
|
|
z
y
Рис. 6.
Ответ: наименьшие отрезки a = 1, b = 1, и c = 2.
Пример 1.11. Определите расстояние между соседними плоскостями, заданными индексами (111), если параметр кубической 3 Å.
Дано: a =3 Å.
Найти: l.
Решение
Искомое расстояние в кубической решетке
G = H: + + = .
Здесь [m n p] – индексы прямой, направленной нормально к системе
плоскостей (h k l).
G = 3Å H1 + 1 + 1 = 3√3 = 5,2 Å .
Ответ: l = 5,2 Å.
Пример 1.12. Плоскость в кубической решетке задана индексами (011), направление прямой − [111]. Определите угол между прямой и плоскостью.
Решение
Синус угла между прямой и плоскостью определяется формулой sin L = : + N + G= .
+ N + G ∙ : + + =
Здесь m, n, p – индексы прямой, h, k, l – индексы плоскости.
13
sin L = 0 |
0 · 1 + 1 · 1 + 1 · 1 |
|
0 + 1 + 1 |
|
|
2 |
|
|
|||||||
+ 1 + 1 |
∙ |
1 + 1 + 1 = √0 + 1 + 1 ∙ √1 + 1 + 1 = √6 . |
|
|
|||||||||||
|
OP Q = 0,82 |
|
=> |
Q = R OP 0,82 = 55 . |
|
0 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
Ответ: ϑ = 55 |
|
||||
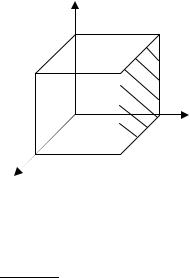
Пример 1.13. Докажите, что в кубической решетке направление оси oy |
|||||||||||||||
параллельно плоскости с индексами (100). |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
Плоскость с указанными в условии индексами |
|
|
z |
|
|
|
|||||||||
показана на рис. 7 (заштрихованная область). |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
Косинус угла между осью oy и нормалью к |
|
|
|
|
|
|
|
||||||||
плоскости определяется формулой |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
:+: + + + =+= |
+ = . |
|
|
|
|
|
|
y |
|||||
|
|
|
|
|
|
|
|
||||||||
cos Q = H:+ + + + =+ ∙ H: |
+ |
|
|
|
|
|
|
|
|||||||
Здесь m, |
n, p – индексы прямой. Индексы оси |
x |
|
|
|
||||||||||
oy [010], индексы нормали к плоскости совпадают с |
|
|
Рис. 7. |
|
|
|
|||||||||
индексами плоскости − [100]. |
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
|
|
1 · 0 + 0 · 0 + 0 · 0 |
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
cos Q = 1 + 0 + 0 |
∙ 0 |
+ 1 + 0 |
= |
√1 ∙ √1 |
= 0. |
|
|
|
|
|||||
(100) и |
|
|
Q = |
|
= 90 |
. |
|
|
|
|
|
|
|
|
|
Следовательно, |
|
U |
[010] |
Так как угол между нормалью к плоскости |
|||||||||||
|
направлением oy |
равен |
900, следовательно, плоскость |
(100) |
|||||||||||
параллельна оси oy [010]. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1.14. Определите угол между плоскостями (110) и (100).
Решение
Первый способ. Косинус угла между плоскостями определяется формулой cos Q = + + N+N + G+G .
H + + N+ + G+ ∙ H + N + G
Здесь h, k, l – индексы плоскости.
14

cos Q = |
1 · 1 + 1 · 0 + 0 · 0 |
1 + 0 + 0 |
1 |
||
1 + 1 + 0 ∙ 1 + 0 + 0 |
= √1 + 1 + 0 ∙ √1 |
= √2 . |
|||
Второй способ. Индексы нормалей к заданным плоскостям [110] и [100]. Тогда |
|||||
|
:+: + + + =+= |
|
|
||
искомый угол можно определить как угол между двумя направлениями в кристалле. |
|||||
|
cos Q = |
H:+ + + + =+ ∙ H: + + = |
. |
|
|
Здесь m, n, p – индексы направления. |
1 + 0 + 0 |
1 |
|||
cos Q = |
1 · 1 + 1 · 0 + 0 · 0 |
||||
1 + 1 + 0 ∙ 1 + 0 + 0 |
= √1 + 1 + 0 ∙ √1 |
= √2 . |
|||
Из первого и второго способа решения следует, что определяемый в задаче угол φ = 450.
Ответ: φ = 450.
Задачи для самостоятельного решения по теме №1
1.Определите число атомов, приходящихся на одну элементарную ячейку в кристаллах с простой и объемноцентрированной кубической структурой.
(Ответ: 2).
2.Сколько атомов приходится на элементарную ячейку в кристаллах с простой и плотноупакованной гексагональной структурой?
(Ответ: 1;2).
3. Вычислите объем элементарной ячейки в кристалле гексагональной сингонии с постоянными a и c. (Ответ: √ a2c).
4.Напишите индексы Миллера для плоскости, содержащей узлы [[200]], [[010]] и [[001]] двумя способами.
(Ответ: (122)).
5. Найдите постоянную кристаллической решетки алюминия (ГЦК).
(Ответ: 4,04Å).
6.Определите постоянную кристаллической решетки ванадия, имеющего структуру ОЦК.
(Ответ: 0,303 нм).
15

7.Определите плотность кристалла KBr, имеющего примитивную кубическую структуру с постоянной a = 0, 659 нм.
(Ответ: 2,74·103 кг/м3).
8.α-железо (α-Fe) имеет структуру ОЦК (а = 2,86 Å), γ-железо (γ-Fe) – структуру ГЦК (а = 3,56 Å). Как изменится плотность железа при переходе α→γ ?
(Ответ: увеличится на 4%).
9.Докажите, что направление [mnp] в кубической решетке нормально к плоскостям (hkl).
10.Найдите угол между плоскостями (100) и (010) кубической примитивной решетки.
(Ответ: φ = 900)
ТЕМА № 2. ТИПЫ СВЯЗЕЙ В ТВЕРДЫХ ТЕЛАХ
2.1. Энергия взаимодействия атомов кристаллической решетки ионного типа
Законы и формулы к решению задачпо теме № 2.1
1. Полная энергия решетки, содержащей N пар ионов: |
|
||||||||
|
|
V = |
− |
" W |
XY |
+ |
F |
|
|
|
|
|
|
\ ]. |
|
||||
|
|
|
|
|
4Z[ R |
|
R |
|
|
|
|
|
|
: |
|
|
|
|
|
2. |
|
|
− |
|
Y |
|
1 |
|
|
Внутренняя энергия кристалла: |
· X 4Z[ R · `1 − a, |
|
|||||||
|
V^_\ |
= |
|
|
· "# |
|
|||
|
Здесь e – заряд |
электрона, |
n – |
постоянная сил |
отталкивания, |
||||
α – |
постоянная Маделунга, NA − число Авогадро, r0 – равновесное расстояние |
||||||||
между частицами, m – масса кристалла, μ − молярная масса, ε0 – |
электрическая |
||||||||
постоянная, b − эмпирическая константа. |
|
|
|
||||||
Примеры решения задач по теме № 2.1
Пример 2.1.1. Рассчитать внутреннюю энергию 200 г каменной соли, постоянная кристаллической решетки которой равна 5,64 Å . Постоянная сил отталкивания 9,4.
16

Дано: m = 200 г = 0,2 кг.
µ = 58,5·10 −3 кг/моль, а = 5,64 Å = 5,64·10 −10 м, n = 9,4,
α = 1,75.
Найти: Umin.
|
|
|
V^_\ = |
− |
|
: |
РешениеY |
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
· "# · X 4Z[ R · `1 − |
a, |
|
|
|||||||||||||
Для решетки |
каменной |
|
|
соли (NaCl) |
равновесное расстояние между |
|||||||||||||||||||
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частицами r0 = . |
|
2Y |
|
|
|
|
|
1 |
|
|
− : |
|
Y |
|
1 |
|||||||||
V^_\ = |
− |
: |
|
|
|
|
|
|
|
= |
|
|
||||||||||||
|
· "# · X 4Z[ · `1 − |
a |
|
|
· "# |
· X 2Z[ · `1 − |
a. |
|||||||||||||||||
|
|
|
|
V^_\ = |
|
− |
|
|
0,2 |
|
− |
|
· 6,02 · 10 |
|
· 1,75 · |
|
|
|||||||
|
|
|
|
|
|
|
|
58,5 · 10 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
−+4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кДж |
|
||
|
|
|
|
|
− |
|
|
|
) |
|
|
− |
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
(1,6 · 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= −2618 |
. |
|
|||||
· 2 · 3,14 · 8,85 · 10 |
|
+ · 5,64 · 10 + · `1 − 9,4a |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Umin.= − 2618 кДж. |
||||
Пример 2.1.2. Как изменится равновесное расстояние r0 между ионами и |
||||||||||||||||||||||||
энергия решетки NaCl, если заряд иона возрастет вдвое? |
|
|
||||||||||||||||||||||
Дано: e, |
2e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти: r02 / r01, |
U02 / U01. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|||||
Полная энергия решетки, содержащей N пар ионов, |
|
|
||||||||||||||||||||||
|
|
|
|
V = |
|
− |
" W |
XY |
|
+ |
F |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4Z[ R |
|
|
|
|
|
|
|
|||||
Из равенства нулю первой производной от энергии кристалла имеем:
17

а) для иона с зарядом е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
" W |
XY |
|
|
− |
|
F |
] = 0 |
|
|
|
или |
|
|
|
|
|
XY |
|
= |
|
|
F |
|||||||
|
|
|
|
\b+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
\b+ . |
|||||||||
4Z[ R + |
|
R + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4Z[ R + |
|
R + |
|||||||||
Умножим уравнение на R\b++ : |
|
|
|
|
|
|
|
|
|
|
|
XY R\)++ |
|
|
|
|
|
||||||||||||
|
XY |
R\b++ |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
= F, |
|
||||||||||
|
4Z[ R + = F |
|
|
|
|
4Z[ F |
|
|
+ |
|
4Z[ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
R + = |
|
a |
\)+ |
; |
|
|
|
|
|
|
|
|
|||||||
б) для иона с зарядом 2е |
|
|
` XY |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4Z[ F |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
\)+ |
. |
|
|
|
|
|
|
|
|
|||||
Искомое отношение: |
|
|
|
|
|
R = `X(2Y) a |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
4Z[ F |
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
R = |
|
|
|
\)+ |
|
`1a |
|
= 4+)\ . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
` |
X(2Y) |
a |
+ = |
\)+ |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
R + |
|
|
|
|
|
|
4 |
|
|
+ |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
` |
4Z[ F |
a |
\)+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отношение энергий: |
|
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(2Y) |
· A1 |
− 1E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
"# · X |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
\ |
|||||||||||||
V+ |
= |
|
|
|
|
|
4Z[ R |
|
|
|
|
= 4 · R = 4 · 4 |
\)+ |
= 4 |
\)+ |
||||||||||||||
|
|
|
|
|
|
Y |
|
|
|
1 |
|
|
|
|
|||||||||||||||
V |
"# |
|
· X |
|
|
· A1 − E |
|
|
|
|
R + |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
4Z[ R + |
|
|
|
|
|
|
|
ccdfde |
= 4fgh |
|
iife = 4hgf |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
h . |
|||||
Пример 2.1.3.CВ выражении полной энергии кристаллической решетки ионного типа член ch , соответствующий силам отталкивания, часто заменяют
C·e− r/ρ , вид которого легче объяснить теоретически. Чему равно расстояние r0 = r0(n, ρ), при котором эти две энергии отталкивания дают одинаковые значения энергии решетки?
18

Дано: n, ρ. Найти: r0.
РешениеXY
V(R) = −" · W4Z[ R j · Y−cd].
− ρ
Определим первую производную при r = r0: |
1 j · Y |
c ] = 0. |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
`-Va |
|
|
|
= " · W |
XY |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
-R cd |
|
|
|
|
|
|
|
|
− |
|
|
|
−ρd |
|
|
|
|
|
|
|
|
|||||
Отсюда |
|
|
|
|
|
|
|
4Z[ R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
XY |
|
1 |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
XY |
|
|
|
c |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4Z[ R |
= j · Y |
− |
|
|
|
|
=> |
|
|
|
|
|
j = |
4Z[ R |
· Y |
ρ |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим этот коэффициент в U(r0): |
|
|
|
· Y |
|
c] = −" · XY |
|
`1 − a. |
|||||||||||||||||||||
V(R ) = −" · W XY |
|
|
|
|
|
XY |
|
· Yc |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|||||
|
|
|
4Z[ R |
|
|
4Z[ R |
|
|
|
|
|
− |
|
|
|
|
4Z[ R |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
||
Сравним последнее выражение для энергии с |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
XY |
|
|
`1 − |
|
|
|
|
|
|
|
|
||||
Из сравнения видно, что |
V(R ) = −" · 4Z[ R |
a. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
=> |
|
|
|
|
|
R = |
. |
|
|
|
|
|
|
||||||
|
|
|
R = |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: r0 = ρ n. |
||||||||||||
Задачи для самостоятельного решения по теме № 2.1
1.Считая, что основная часть энергии кристалла ионного типа обусловлена кулоновским, т.е. электростатическим, взаимодействием, определите энергию 200 г каменной соли, постоянная решетки которой а = 5,64 Å. Воспользовавшись решением задачи № 2.1.1, оцените в процентах долю энергии отталкивания в общей энергии данного кристалла каменной соли.
19

2.С какой силой взаимодействуют между собой соседние ионы цезия и хлора в кристалле хлористого цезия?
(Ответ: 1,8·10-9 Н).
2.2Теория теплоемкости твердых тел
(классическая и квантовая по Эйнштейну)
Законы и формулы к решению задачпо теме № 2.2
1. Внутренняя энергия твердого тела по классической теории:
V = 3ν kl.
Здесь ν − количество вещества.
2. Средняя энергия одномерного квантового осциллятора при T ¹ m = "2ħn + Y "oħ−n1 .
ħpq
3. Средняя энергия трехмерного квантового осциллятора при T ¹ m = 3"2ħn + 3"ħn
Y o − 1
ħpq
0:
0
Здесь N – количество осцилляторов, ω − круговая частота колебаний осциллятора.
4. Характеристическая температура Эйнштейна: r = n.
ħN
Здесь ħ − постоянная Дирака, k − постоянная Больцмана.
Примеры решения задач по теме №2.2
Пример 2.2.1. Найдите удельные теплоемкости кристаллов алюминия и меди по классической теории.
Дано: µ Al = 26,98·10 −3 кг/моль. µ Cu = 63,55·10 −3 кг/моль.
Найти: cAl, cCu.
20
