540

Величину tкр находим по статистической таблице или по функции: =СТЬЮДРАСПОБР(0,05;32), принимая уровень значимости α = 0,05, число степеней свободы f = = n – 1 = 32. В результате находим, что критическое значе-

ние tкр = 2,036933.

Сравнение |tнабл | и tкр показало, что к значимым коэффициентам регрессии относятся только четыре выделенных

в табл. 5.10 коэффициента.

Анализ данных табл. 5.9 показывает, что значимая корреляционная связь существует между: 1) содержанием нерастворимого остатка и содержанием NaC1 и СаSO4; 2) содержанием КС1 и NaC1; 3) содержанием СаSO4 и бро- мид-ионом. По знаку коэффициентов корреляции можно заключить, что чем меньше содержание в сильвинитовой руде хлорида натрия и выше содержание сульфата кальция, тем больше содержание в руде нерастворимого остатка. Содержание основного вещества КС1 в руде возрастает при снижении содержания примеси хлорида натрия. Содержание примеси бромид-иона снижается при увеличении в руде примеси сульфата кальция. По величине коэффициента корреляции можно заключить, что наибольшая корреляционная связь существует между основными компонентами сильвинитовой руды – хлоридами КС1 и NaC1 (r = –0,872).

191

Найденные зависимости полезны для оптимизации работы флотационных и галургических производств, перерабатывающих сильвинитовые руды.

6. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Одной из важнейших задач экспериментальных исследований является поиск математических зависимостей (моделей), описывающих полученные данные. Математические модели объективно и в сжатой форме представляют полученную информацию, которая в дальнейшем может быть использована для расчета оборудования, проектирования технологии или управления промышленными процессами. Математическую обработку экспериментальных данных проводят в основном с использованием компьютерных программ или графическим методом (при отсутствии компьютеров).

В основе компьютерной обработки положен метод наименьших квадратов, суть которого будет рассмотрена ниже. По этому методу в результате математической обработки находят коэффициенты известных уравнений, применимых в определенных условиях, или уравнений регрессии, описывающих любые процессы в заданном диапазоне варьирования переменных. В отличие от уравнений, описывающих физико-химические закономерности, уравнения регрессии имеют чисто эмпирический характер и не объясняют законы природы.

6.1. Нахождение уравнений графическим методом

При отсутствии компьютера обработку экспериментальных данных проводят графически. Если экспериментальная зависимость между аргументом Х и функцией Y описывается уравнением прямой линии

192

то описание экспериментальных данных сводится к нахождению коэффициентов уравнения а и b путем построения графика Y = f(X) в осях координат Х и Y. Коэффициент а находят по величине отрезка, отсекаемого прямой на оси Y при Х = 0, а величину коэффициента b вычисляют по тангенсу угла наклона прямой к оси Y.

Если экспериментальная зависимость между аргументом Х и функцией Y представляет криволинейную зависимость, то для нахождения уравнения, описывающего экспериментальные данные, проводят преобразование нелинейных экспериментальных зависимостей к линейным. Линеаризацию проводят преобразованием осей координат и/или введением дополнительных переменных. При этом в качестве уравнений могут использоваться известные из теории уравнения кинетики.

Рассмотрим примеры линеаризации для типичных уравнений, описывающих экспериментальные данные.

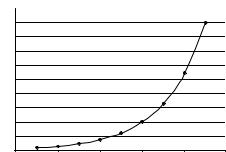
Пример 1. Степенная зависимость описывает кривую,

представленную на рис. 6.1.

Уравнение степенной зависимости имеет вид

где а, b – коэффициенты уравнения.

193

Для нахождения коэффициентов а и b проводят логарифмирование уравнения (6.2):

и переходят к новым координатам ln Y и ln (Х), в которых строят график, логарифмируя экспериментальные данные. По графику ln Y = f(ln (Х)) определяют величину отсекаемого отрезка ln (а) на оси ln Y и величину коэффициента b:

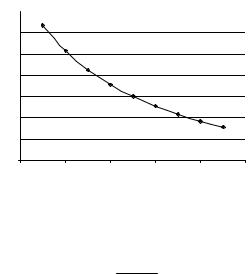
Пример 2. Экспоненциальная зависимость описывает кривую, представленную на рис. 6.2.

Уравнение экспоненциальной зависимости имеет вид

где а, b – коэффициенты уравнения.

Логарифмирование уравнения (6.5) позволяет перевести уравнение в линейный вид:

194

По графику lnY = f(Х) определяют величину отсекаемого отрезка ln(а) на оси lnY, вычисляя затем величину коэффициента а и величину коэффициента b:

Аналогичные расчеты проводят при поиске констант b и n известного уравнения Ерофеева, описывающего кинетическую область протекания химических превращений:

Пример 3. Обратная зависимость описывает кривую,

представленную на рис. 6.3.

Уравнение обратной зависимости имеет вид

Для вычисления коэффициентов а и b переходят к новой переменной Y = 1/Y. Отсюда, уравнение (6.8) примет вид

195

Для нахождения коэффициентов а и b строят график в координатах Y = f(X) (см. рис. 6.3) и производят вычисление отсекаемого отрезка на оси Y и тангенса угла наклона к оси Х.

Пример 4. Полином второй степени описывает криво-

линейную зависимость, приведенную на рис. 6.4.

Уравнение полинома второй степени имеет вид

где а, b, с – коэффициенты полинома.

Для вычисления искомых коэффициентов вводят новую переменную:

где x1, y1 – координаты произвольной точки, взятой на экспериментальной кривой.

С учетом введенной переменной и уравнения (6.11) находят величину Y:

где (b + сХ1) = соnst.

196

Из уравнения (6.13), построив график по экспериментальным данным в координатах Y = f(Х), находят величину коэффициента b по величине отрезка, отсекаемого на оси

дят по тангенсу угла наклона прямой к оси Х. Коэффициент а вычисляют из уравнения

где n – число значений Х, по которым производится суммирование.

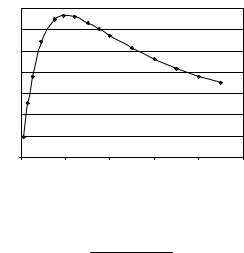
Пример 5. Описание кривых с экстремумом. Для кри-

вой с экстремумом, изображенной на рис. 6.5, используют уравнение следующего вида:

Для нахождения коэффициентов уравнения (6.15) вводят переменную z = x/y и приходят к виду уравне-

ния (6.11), т.е.

197

Вычисление коэффициентов уравнения (6.15) производится аналогично вычислению коэффициентов уравне-

ния (6.11).

Примеры 4, 5 показывают, что вычисление коэффициентов уравнений графическим путем сопряжено с длительной процедурой построения графиков и расчетов. Целесообразнее такие расчеты производить на компьютерах, ускоряющих расчеты и позволяющих из тысяч уравнений находить самые точные, работающие в широком диапазоне изменения переменных. Такие расчеты проводят с помощью пакетов прикладных программ.

6.2. Регрессионный анализ

Регрессионный анализ часто используют в промышленности для описания результатов пассивного или активного промышленного эксперимента в виде линейных (6.17) или нелинейных (6.18) уравнений регрессии:

m

Yi = a0 + a1x1 + а2x2 + а3x3 + ... + аixi = a0 + ∑ai xi , (6.17)

i=1

Yi = а0 + а1x1 + а2x2 + а12x1x2 + а11x12 + а22x22 +... =

где Yi – выходной параметр (степень превращения, степень извлечения, содержание основного вещества, длительность процесса и т.п.);

xi – входные параметры, влияющие на выходной параметр (температура, концентрация, давление и т.п.);

а0, аi – коэффициенты регрессии;

m – количество входных параметров.

При проведении пассивного эксперимента процесс проводится в рамках установленных технических норм, входные и выходной параметры регистрируются на компь-

198

ютере или в технологическом журнале. Как правило, указанные параметры и регламентные различаются незначительно, поэтому результаты промышленного пассивного эксперимента представляются линейными уравнениями регрессии.

При проведении активного эксперимента (в котором экспериментатор активно влияет на условия проведения эксперимента) диапазон изменения входных и выходных величин существенно расширяется. В этом случае результаты активного эксперимента представляются нелинейными уравнениями регрессии, более точно описывающими многомерные функции выходного параметра Yi.

Уравнения регрессии (6.17), (6.18) представляют математическую модель изучаемого объекта только для того диапазона, в котором проводилось исследование объекта. При расширении диапазона изменения входных переменных найденные уравнения регрессии (коэффициенты регрессии) становятся некорректными и должны быть пересчитаны. Вычисляемые коэффициенты и уравнения регрессии не имеют физического смысла и для одного и того же объекта (процесса) может быть найдено несколько уравнений регрессии, отличающихся точностью описания изучаемого объекта. Уравнения регрессии могут использоваться для оптимизации изучаемых процессов.

Выбор того или иного уравнения регрессии зависит от исследователя и определяет точность (адекватность), с которой уравнение описывает в требуемых пределах исследуемый (наблюдаемый) объект. Такой выбор уравнения определяется исследователем на основании априорных сведений об объекте, влияющих факторов и удобства использования математической модели конкретного вида. Методы регрессионного анализа позволяют из нескольких различных по виду моделей выбрать наиболее адекватную.

Регрессионный анализ сводится к определению коэффициентов уравнения регрессии (на основании экспериментальных данных), к оценке значимости этих коэффициентов и степени адекватности математической модели. Для

199

проведения регрессионного анализа полученные массивы данных пассивного или активного эксперимента обрабатываются, производится отсев неверных значений, далее, после устранения ошибок данные подвергаются математической обработке и представляются в виде функции регрессии одной или более переменных.

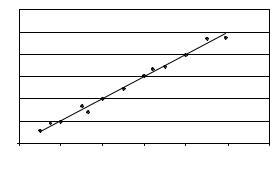
Вычисление коэффициентов регрессии проводится по методу наименьших квадратов. Суть метода заключается в следующем. Пусть входные и выходные параметры имеют линейную корреляционную связь, тогда при оценке выходного параметра используется линейное регрессионное уравнение вида (6.17). Необходимо найти коэффициенты регрессии а0, аi (i = 1, ..., m, m – число коэффициентов уравнения регрессии), такие, чтобы экспериментальные точки yj (j = 1, …, n, n – число экспериментальных наблюдаемых точек), построенные по данным наблюдений, лежали как можно ближе к расчетной прямой Y = f(x), вычисляемой по уравнению регрессии (рис. 6.6).

Для нахождения коэффициентов регрессии составляют функцию квадратов отклонений расчетных и экспериментальных (наблюдаемых) значений:

200