Типовые планетарные механизмы

№	Структурная схема механизма	Uред	КПД
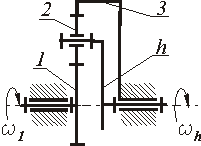
1		3....10	0.97....0.99
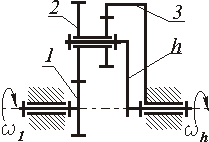
2		7....16	0.96....0.98
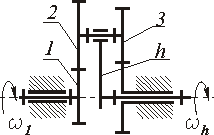
3		25....30	0.9....0.3
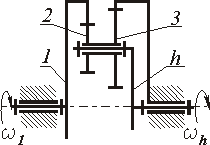
4		30....300	0.9....0.3

Формула Виллиса

Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним и одним внутренним зацеплением. Всему механизму сообщается угловая скорость равная по величине и противоположна по направлению угловой скорости водила, при этом водило остановится, а опорное колесо начнет поворачиваться. Таким образом, планетарный механизм превратится в механизм с неподвижными осями, состоящий из нескольких последовательно соединенных зубчатых колес. Такой механизм носит название обращенного механизма.

Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице

В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось сателлита подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.

Передаточное отношение обращенного механизма 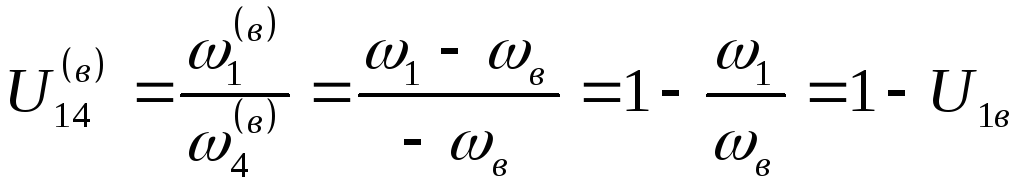, окончательно передаточное отношение планетарного редуктора может быть определено по формуле Виллиса:

Передаточное отношение планетарного редуктора от любого колеса к водилу равно единице минус передаточное отношение обращенного механизма от этого колеса к опорному.

Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами

1. Двухрядный механизм с одним внутренним и одним внешним зацеплением.

Дано: Кинематическая схема механизма числа зубьев колес;

Определить: Передаточное отношение механизма.

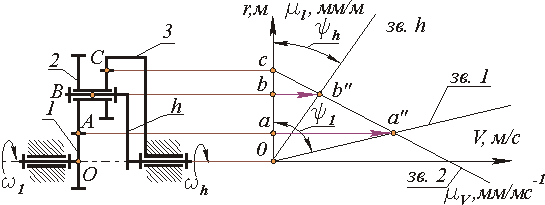
Аналитическое определение передаточного отношения.

Заданный планетарный механизм с одним внешним и одним внутренним зацеплениями зубчатых колес. Применяем метод обращенного движения.

Аналитическое определение передаточного отношения основывается на формуле:

,

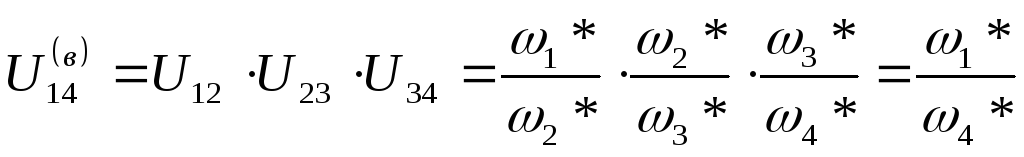так как колеса 2-3 находятся на одном валу, соответственно вращаются с одинаковой угловой скоростью.

Используя основную теорему Виллиса, для заданного обращенного механизма получим:

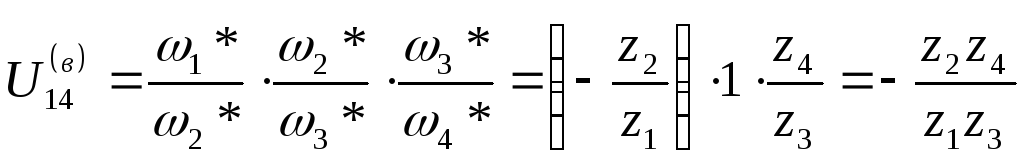
По формуле Виллиса

Графическое определение передаточного отношения.

В системе координат построим треугольники распределения линейных скоростей звеньев.

Для чего

• на схеме редуктора отмечаются характерные точки; центра колес и точки зацеплений, которые выносятся на вертикальную ось радиусов. Вычисляется скорость первого колеса 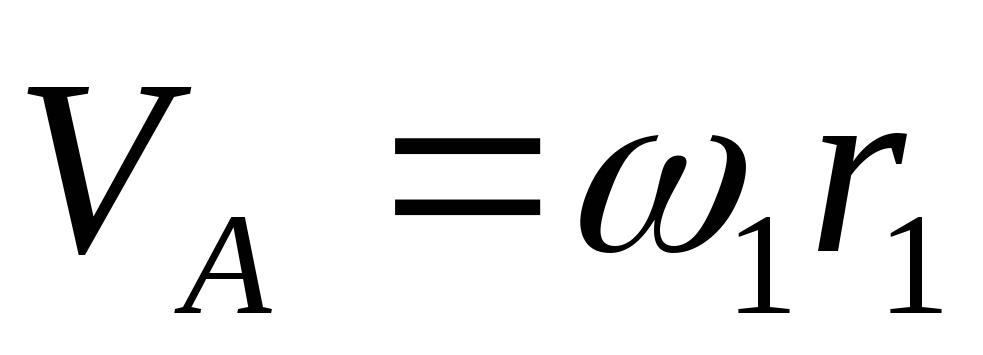(или водила).

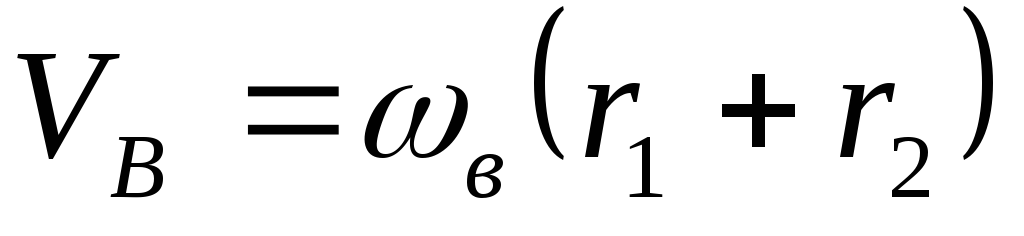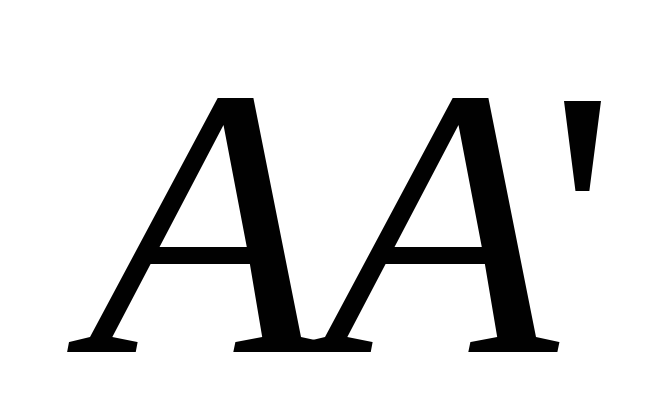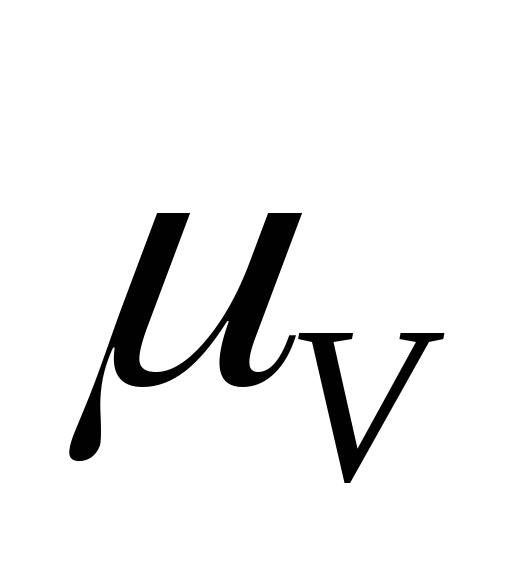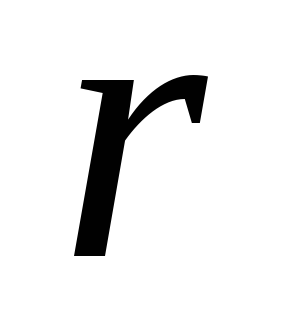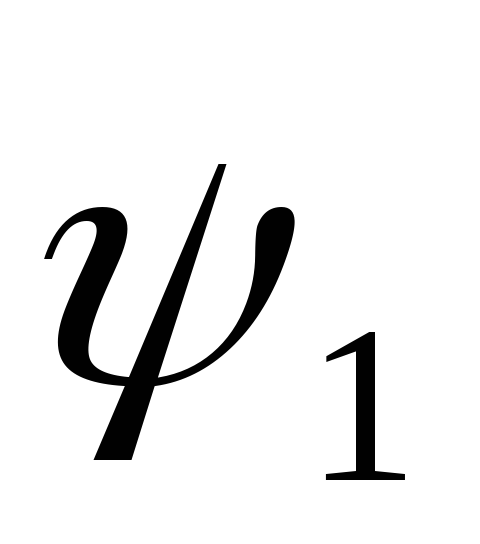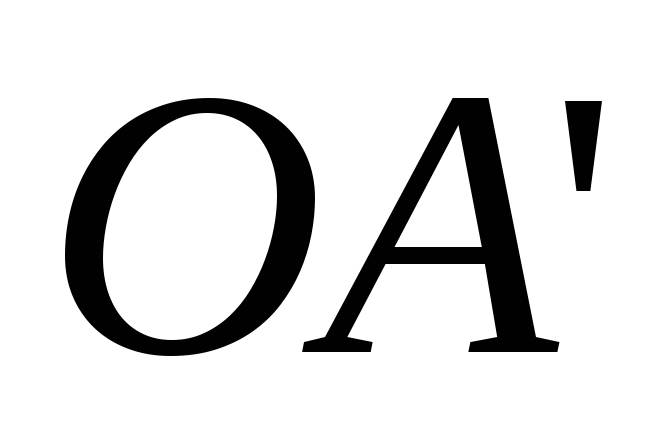• в произвольном масштабе откладываем отрезок, выражающий в масштабескорость точки. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена, лежащих на оси.Эта прямая образует с осьюугол. Отрезок– линия распределения скоростей первого звена (лрс 1).

• Так как в точке скорость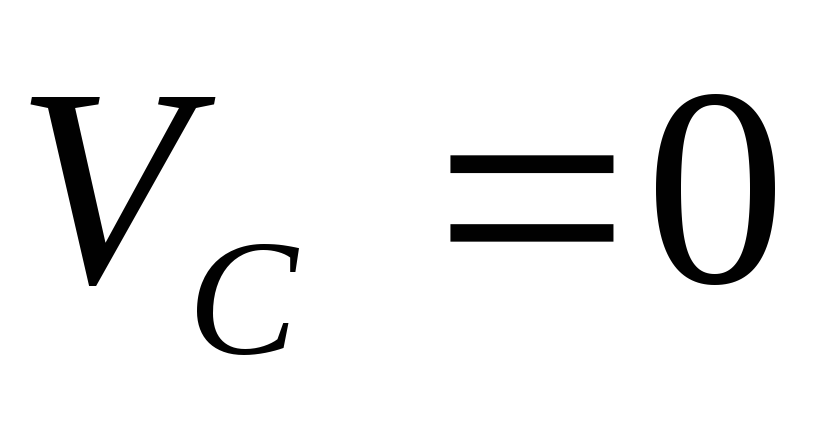, строим линию распределения скоростей блока сателлитов (лрс бл.с.), соединяя точкуи.

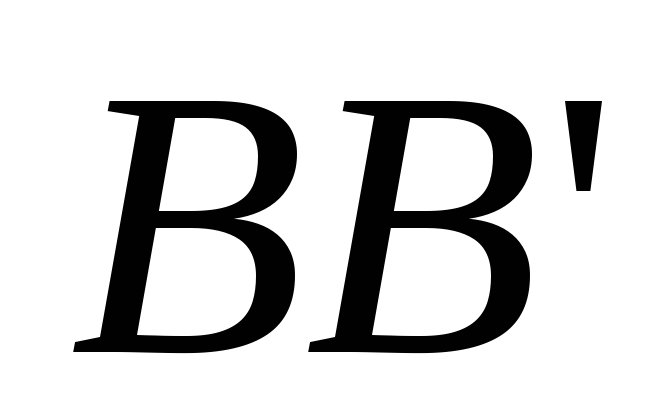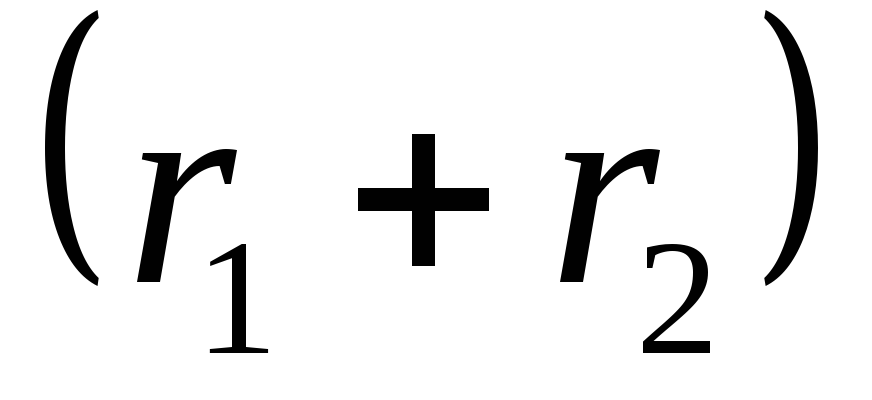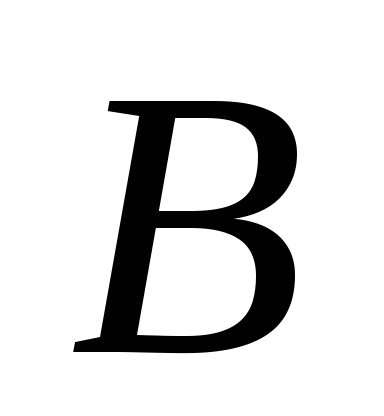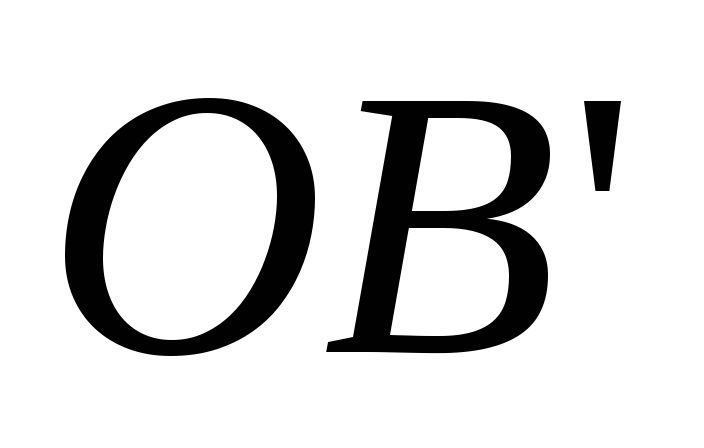• Строим отрезок для радиуса, выражающий в масштабескорость точки. Отрезок– линия распределения скоростей водила (лрсв).

• Обозначим точку пересечения скорости точки первого колеса с лрсв

,

,

,

.
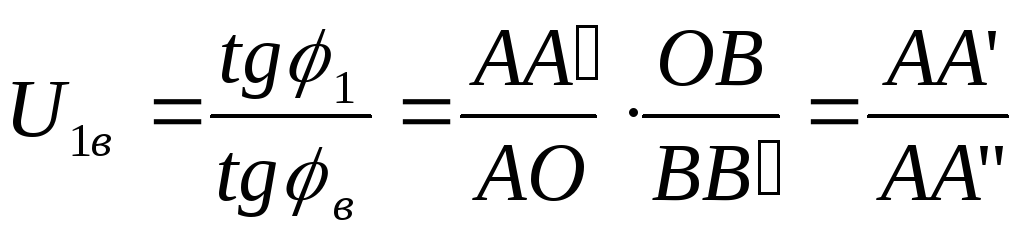