ЛЕКЦИЯ 14

Кинематика планетарных механизмов

   Краткое содержание: Многозвенные зубчатые механизмы. Кинематика рядового зубчатого механизма. Кинематика ступенчатого механизма. Формула Виллиса для планетарных механизмов. Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.

Многозвенные зубчатые механизмы

При проектировании зубчатых механизмов многих машин и приборов (манипуляторов, станков, автомобилей, летательных аппаратов, индикаторов, тахометров, печатающих устройств ЭВМ и др.) возникает необходимость обеспечить передачу вращения с большим передаточным отношением или при значительных межосевых расстояниях. В таких случаях применяют многозвенные зубчатые механизмы либо снижающие скорость вращения выходного вала по сравнению с входным — редукторы, либо повышающие ее — мультипликаторы.

Многозвенные зубчатые механизмы могут быть как плоскими, так и пространственными. Они подразделяются на два основных вида:

зубчатые механизмы с неподвижными осями всех колес;

зубчатые механизмы, оси отдельных колес которых перемещаются относительно стойки.

К первому виду механизмов относятся рядовые (с развернутой схемой) и ступенчатые зубчатые механизмы, подвижность таких механизмов . Ко второму виду относятся планетарные, дифференциальные, замкнутые дифференциальныеи волновые зубчатые механизмы. Большим достоинством механизмов второго вида является их компактность. Проектирование многозвенных зубчатых механизмов включает два этапа: выбор структурной схемы; определение чисел зубьев для воспроизведения заданного передаточного отношения.

Общее передаточное отношение многозвенного механизма равно произведению передаточных отношений отдельных механизмов (ступеней), последовательно включенных в его состав

Кинематика рядового зубчатого механизма

Рядовым зубчатым механизмомназывается сложный зубчатый механизм с неподвижными осями колес, образованный последовательным соединением нескольких пар единичных зубчатых колес. Имея схему передачи и числа зубьев или радиусы начальных окружностей колес можно определить общее передаточное отношение такого редуктора аналитически или графически. (Для колес без смещения, которые обычно используют в редукторах, начальные окружности совпадают с делительными; для колес со смещением -

).

Рассмотрим кинематику рядового механизма составленного из трех зубчатых передач внешнего зацепления. Схема механизма изображена на рис.

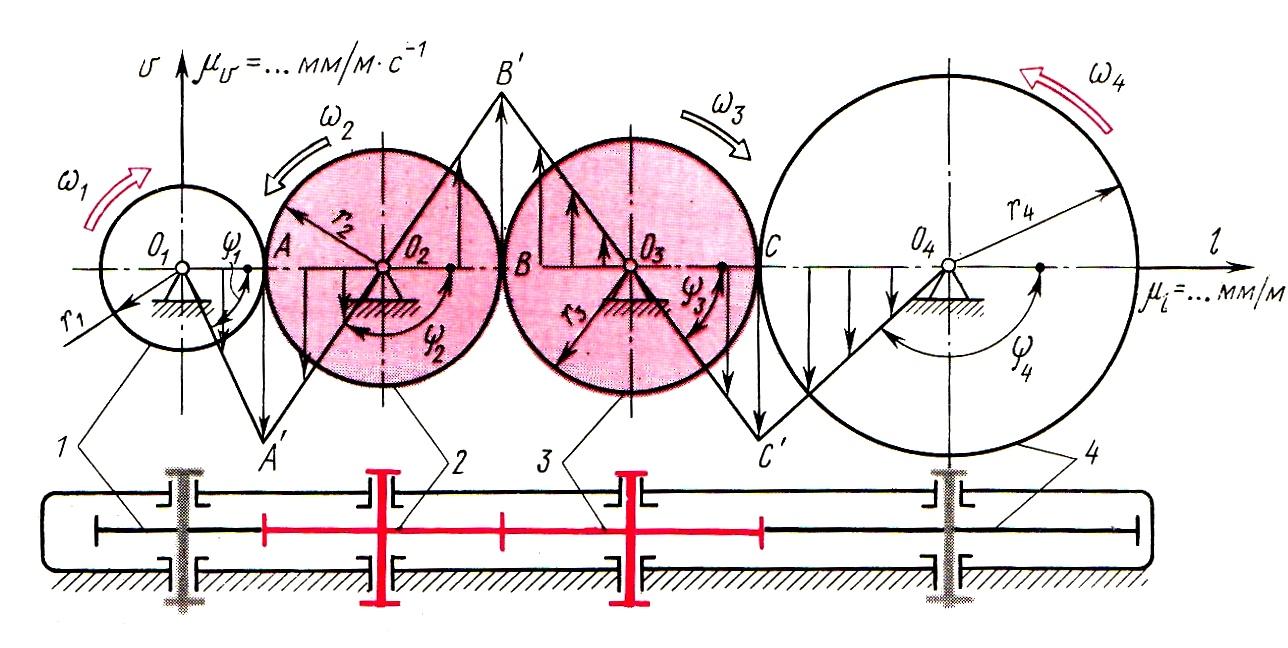
Аналитическое определение передаточного отношения

Аналитическое определение передаточного отношения основывается на формуле:

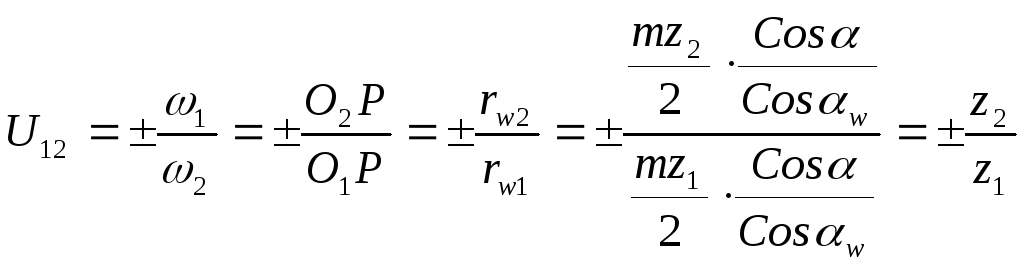, где знак «+» соответствует внешнему зацеплению зубчатых колес, а знак «-» внутреннему.

Таким образом, для приведенного механизма получим:

На основе чего можно получить общую формулу для определения передаточного отношения рядового редуктора:

.

Общее передаточное отношение рядового зубчатого механизма постоянно и равно обратному отношению чисел зубьев или радиусов крайних колес. Знак передаточного отношения определяется множителем , где- число передач внешнего зацепления.