
2929
.pdf
55
Б435 СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Г.В. Белоненко, О.В. Соболева
ГИДРОЛОГИЯ И ГИДРОТЕХНИЧЕСКИЕ СООРУЖЕНИЯ
Методические указания к практическим занятиям
Новосибирск
2015
1
УДК 556(076.5)+626/627(076.5)
Б435
Белоненко Г.В., Соболева О.В. Гидрология и гидротехниче-
ские сооружения: Метод. указ. к практ. занятиям. – Новосибирск: Изд-во СГУПСа, 2015. – 36 с.
Разработаны в соответствии с программой дисциплины «Гидрология и гидротехнические сооружения» и содержат различные варианты заданий и методические указания к их выполнению.
Предназначены для студентов направления «Строительство» (профиль «Водоснабжение и водоотведение») и могут быть полезны студентам иных специальностей при выполнении ими расчетов речного стока.
Рассмотрены и рекомендованы к изданию на заседании кафедры «Гидравлика, водоснабжение, водные ресурсы и экология».
О т в е т с т в е н н ы й р е д а к т о р д-р геогр. наук, проф. Г.В. Белоненко
Р е ц е н з е н т ы :
канд. техн. наук, доц. Е.Ф. Петров, канд. геогр. наук, доц. Ж.А. Тусупбеков (кафедра «Природообустройство, водопользование и водные ресурсы» ОмГАУ)
©Сибирский государственный университет путей сообщения, 2015
©Белоненко Г.В., Соболева О.В., 2015
2
Введение
Цель практических занятий по дисциплине «Гидрология и гидротехнические сооружения» – закрепление теоретических знаний и приобретение практических навыков по темам:
тема 1 – «Расчеты годового и максимального стока при наличии и отсутствии данных гидрометрических наблюдений»;
тема 2 – «Определение параметров водохранилища сезонного регулирования стока без учета потерь»;
тема 3 – «Определение основных параметров водосбросных сооружений и грунтовой плотины водохранилищного гидроузла».
По каждой теме на основе индивидуальных для каждого студента исходных данных выполняются расчетные упражнения, которые иллюстрируются графиками и таблицами, содержащими результаты расчетов.
Выполнение упражнений предполагает обязательное обращение студентов к учебной, нормативной и специальной литературе по гидрологии, регулированию речного стока и гидротехническим сооружениям.
Тема 1. Расчеты годового и максимального стока при наличии и отсутствии данных гидрометрических наблюдений
Упражнение № 1. Расчеты годового стока при наличии данных наблюдений
Цель работы: определение годового стока (расхода и объема) заданной расчетной обеспеченности.
3
Исходные данные: результаты многолетних гидрометрических наблюдений за стоком реки в заданном створе (прил. А) – среднегодовые расходы воды Qi, м3/с (прил. Б).
Требуется:
1. Определить норму годового стока – расход Q0, м3/с, объем W0, млн м3/год.
2.Оценить изменчивость стока Cv.
3.Подобрать теоретическую кривую обеспеченности и опре-
делить годовой сток расчетной обеспеченности Qр%, м3/с, Wр%, млн м3/год.
4. Выполнить внутригодовое распределение стока Wр% расчетной обеспеченности.
Порядок выполнения.
В данном упражнении статистические параметры теоретической кривой обеспеченности годового стока – норма Q0, коэффициент вариации Cv и коэффициент асимметрии Cs – определяются методом моментов. Расчеты выполняются в табличной форме
(табл. 1.1).
Таблица 1.1
Расчет параметров кривой обеспеченности годового стока
Год |
Qi |
Qi убыв |
Кi |
Кi 1 |
(Кi – 1)2 |
m |
P, % |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1951 |
|
|
|
|
|
1 |
|
1952 |
|
|
|
|
|
2 |
|
… |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
1970 |
|
|
|
|
|
|
|
|
ΣQi |
– |
ΣКi = n |
Σ(Кi 1) = 0 |
Σ(Кi – 1)2 |
– |
– |
1. Норма годового стока, м3/с,
Q |
|
0 |
|
рассчитывается по формуле
|
i |
|
|
|
|
Q |
, |
(1.1) |
|
n |
||||
|
|
|||
где ΣQi сумма среднегодовых расходов исследуемого ряда; n – число членов ряда.
2. Выполняется ранжирование исходного ряда, для чего исходные значения расходов располагаются в убывающей последо-
4

вательности (от максимального до минимального значения). Результаты записываются в графу 3.
3. Рассчитываются модульные коэффициенты каждого расхода ранжированного ряда: Кi = Qi /Q0 (графа 4). При этом обязательно соблюдение условия ΣКi = n. Среднему значению расхода соответствует значение Кi = 1.
4. Рассчитываются отклонения Кi ранжированного ряда от среднего значения, т.е. находятся значения (Кi – 1). Результаты расчетов заносятся в графу 5. Проверкой правильности расчетов является обязательное соблюдение условия Σ(Кi – 1) = 0.
5.Для каждого члена вариационного ряда находятся значения (Кi – 1)2 и их сумма (графа 6).
6.Каждому значению расхода убывающего ряда Qiубыв присваивается порядковый номер m (от m = 1 до m = n (графа 7)).
7.Рассчитывается эмпирическая обеспеченность P, % (графа 8), каждого расхода вариационного ряда по формуле
P |
m |
100 %. |
|
n |
|||
|
1 |
8. Оценивается временная изменчивость средних расходов, т.е. рассчитывается коэффициент вариации Cv:
(1.2)
годовых
|
|
|
(Ki |
1) |
2 |
C |
|
|
. |
||
v |
n 1 |
|
|||
|
|
|
|
||
|
|
|
|
|
(1.3)
Значение (n – 1) в формуле (1.3) применяется при условии, если n < 30.
9. Выполняется оценка среднеквадратических ошибок вычисления нормы и коэффициента вариации по формулам:
ошибка нормы годового стока, %,
|
|
|
100 |
Cv |
; |
(1.4) |
|
Q |
|
|
|
||||
|
|||||||
|
|
|
n |
|
|||
|
|
|
|
|
|||
ошибка коэффициента вариации, %,
|
100 |
|
|
n (1 C )2 |
|
|
|
|
Cv |
|
|
|
|
v |
. |
(1.5) |
|
n 4C 2 |
2 |
|||||||
|
|
v |
|
|
|
|
|
|
По результатам расчетов εQ и Cv делается вывод о достаточности (или недостаточности) исследуемого ряда для определения
5
нормы и коэффициента вариации. Продолжительность ряда счи-
тается достаточной, если εQ и |
C |
не превышают 5–10 и 10–15 % |
|
|
v |
соответственно. |
|
|
10.Значение коэффициента асимметрии Cs при n < 100, как правило, не рассчитывается, а принимается по наилучшему соответствию теоретической кривой обеспеченности эмпирическим данным.
11.По данным граф 4 и 8 на лист миллиметровой бумаги формата А4 (ориентация альбомная) в координатах Кi (ось ординат) и P, % (ось абсцисс), наносятся эмпирические точки.
12.Задаются тремя значениями коэффициента асимметрии (Cs = Cv, Cs = 2Cv и Cs = 3Cv) и рассчитывают соответствующие этим значениям Cs и Cv ординаты теоретических кривых обеспе-
ченности:
(1.6)
где Фр% – число Фостера – нормированные отклонения ординат от середины при Cv = 1 (принимаются по таблицам прил. В). Результаты расчетов Кр% сводятся в табл. 1.2.
Таблица 1.2
Ординаты теоретических кривых обеспеченности
Расчетный |
|
|
|
|
Обеспеченность P, % |
|
|
|
|
|||||
параметр |
1 |
3 |
5 |
10 |
20 |
|
30 |
40 |
50 |
75 |
80 |
90 |
95 |
99 |
|
|
|
|
|
|
Cs = Cv |
|
|
|
|
|
|
||
Фp% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кр% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cs = 2Cv |
|
|
|
|
|
|
||
Фp% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кр% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cs = 3Cv |
|
|
|
|
|
|
||
Фp% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кр% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. По данным табл. 1.2 (Кр% и Р, %) на исходном листе миллиметровой бумаги формата А4 (рис. 1.1) строятся теоретические кривые обеспеченности.
6
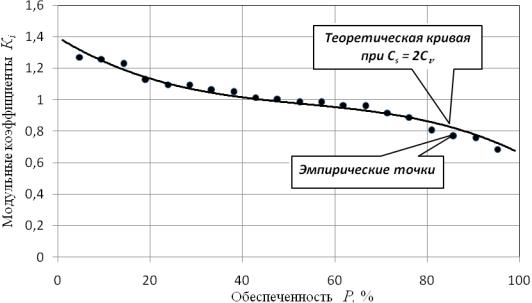
Рис. 1.1. Эмпирические точки (•) и теоретическая кривая обеспеченности при Cs = 2Cv
Анализируя соответствие теоретических кривых обеспеченности эмпирическим данным (в нижней части кривых), делают заключение об окончательном значении Cs для исследуемого ряда расходов.
14. В соответствии с заданием определяют расход Qp%, м3/с, и объем Wp%, млн м3/год, годового стока 95 % обеспеченности:
Q95% = К95%Q0, |
(1.7) |
W95% = 31,54Q95%, |
(1.8) |
где К95% модульный коэффициент 95 % обеспеченности, снятый
сокончательно принятой теоретической кривой обеспеченности.
15.Выполняется распределение полученного объема годового стока W95% внутри года (по месяцам), и находятся объемы притока за каждый месяц (от января до декабря). В данном упражнении внутригодовое распределение Wp% выполняется на основе рекомендаций, полученных в результате научных обобщений особенностей внутригодового распределения годового стока рек бассейна Верхней Оби (прил. Г). По результатам расчетов составляется табл. 1.3 и диаграмма (рис. 1.2) внутригодового распределения годового стока 95 % обеспеченности.
7

Таблица 1.3
Пример внутригодового распределения стока 95 % обеспеченности, млн м3
Объем |
|
|
|
|
|
Месяц |
|
|
|
|
|
Год |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W95%i |
49,3 |
49,3 |
49,3 |
333,3 |
1461,6 |
769,3 |
236,7 |
236,7 |
236,7 |
236,7 |
236,7 |
49,3 |
3 944,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W, млн м³
1600 1400 1200 1000 800 600 400 200 0
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
|
Месяцы |
|
|
|
|
|
|
Рис. 1.2. Внутригодовое распределение стока 95 % обеспеченности
Упражнение № 2. Расчеты максимального стока при наличии данных наблюдений
Цель работы: овладение методами определения максимальных расходов весеннего половодья при достаточности гидрометрических данных.
Исходные данные: результаты многолетних гидрометрических наблюдений за стоком реки в заданном створе – максимальные расходы воды Qmaxi, м3/с (прил. Е), класс капитальности сооружений (прил. Д).
Требуется:
1.Определить норму максимального стока Qmax0, м3/с.
2.Оценить изменчивость стока Cv.
3.Подобрать теоретическую кривую обеспеченности и опреде-
лить максимальные расходы расчетной обеспеченности Qmaxp%, м3/с (для нормальных и чрезвычайных (особых) условий эксплуатации).
8
4. Определить общую продолжительность половодья Т, а также фаз подъема tп и спада tсп, построить гидрограф максимальных расходов для нормальных и чрезвычайных условий эксплуатации, определить объем весеннего половодья.
Порядок выполнения.
В настоящем упражнении статистические параметры максимальных расходов определяются графоаналитическим методом Г.А. Алексеева.
1. Выполняется ранжирование исходного ряда, при котором исходные значения максимальных расходов располагаются в убывающей последовательности (от наибольшего до наименьшего значения).
Каждому значению расхода убывающего ряда Qmaxубывi присваивается порядковый номер m (от m = 1 до m = n).
3.Рассчитывается эмпирическая обеспеченность P, %, каждого расхода вариационного ряда.
4.По полученным данным на миллиметровой бумаге форма-
та А4 в координатах
Q |
убыв |
, |
|
||
max |
|
|
м3/с, и P, %, выносятся эмпирические
точки и на глаз пунктирной линией строится плавная, хорошо усредняющая эмпирические точки, кривая обеспеченности (эмпирическая кривая).
5. На построенной кривой снимаются три опорные значения Qmax, соответствующие 5, 50 и 95 % обеспеченности, т.е. Q5%,
Q50% и Q95%.
6. Для оценки асимметрии кривой обеспеченности рассчиты-
вается коэффициент скошенности |
|
S = (Q5% + Q95% − 2Q50%) / (Q5% − Q95%). |
(1.9) |
По значению S определяется коэффициент асимметрии Cs |
|
(см. прил. В) или рассчитывается по формуле |
|
Cs = 4,9S – 0,3. |
(1.10) |
7. По таблице нормированных отклонений (см. прил. В) по значению Cs для обеспеченностей Р, равных 5, 50 и 95 %, определяются числа Фостера Ф5%, Ф50% и Ф95%.
8. Рассчитывается среднеквадратическое отклонение Qmax,
м3/с, по формуле |
|
σQ = (Q5% – Q95%) / (Ф5% – Ф95%). |
(1.11) |
9
9. Находится среднее арифметическое значение Qmax0, м3/с, равное:
Qmax0 = Q50% – σQФ50%, |
(1.12) |
10. Рассчитывается коэффициент вариации максимальных |
|
расходов по формуле |
|
Cv = σQ / Qmax0. |
(1.13) |
11.С использованием значений Cv, Cs и Qmax0 для интервала
Р= 0,1…99,0 % рассчитываются ординаты теоретической кривой обеспеченности:
(1.14)
(1.15)
Результаты расчетов ординат теоретической кривой обеспеченности заносятся в таблицу, по данным которой строится теоретическая кривая обеспеченности, оценивается ее совпадение с эмпирическими точками и устанавливаются максимальные расходы расчетной вероятности превышения Qmaxp% для нормальных
ичрезвычайных условий эксплуатации:
12.Определяется общая продолжительность весеннего половодья Т, а также продолжительность фаз подъема tп и спада tсп с точностью до суток.
Значение Т, сут, рассчитывается по зависимости, полученной В.В. Лоскутовым для рек Западной Сибири:
Т = К1F0,2h0,4, |
(1.16) |
где К1 = 1,5…1,7 – коэффициент, характеризующий |
условия |
формирования стока; F – площадь речного бассейна, км2 (см. прил. А); h – средний слой стока весеннего половодья, мм (см. прил. А).
Продолжительность фаз подъема и спада половодья опреде-
ляется по зависимостям: |
|
|
|
tп = 0,35Т; |
tсп = 0,65Т. |
(1.17) |
|
Гидрограф притока схематизируется по треугольнику, а ор- |
|||
динаты гидрографа рассчитываются по зависимостям: |
|
||
– для фазы подъема |
|
|
|
Qt = Qmaxp% |
t |
; |
(1.18) |
|
|||
|
tп |
|
|
10
