
Элементы математической физики
..pdfДля выделения частного решения уравнения (1.2) из общего необходимо задать два дополнительных условия для нахождения конкретных значений постоянных c1 и c2.
Первый способ – задать начальные условия (условия Коши). Для уравнения (1.2) условия Коши имеют следующий вид:
y(x0) = y0, y′(x0) = y10, |
(1.4) |
где x0, y0 и y10 – заданные числа.
Справедлива теорема, условия которой гарантируют существование и единственность решения задачи Коши (1.2), (1.4).
Теорема (существования и единственности решения задачи Коши (1.2), (1.4)). Если функция f (x, y, u) непрерывна по аргументу x на промежутке [a, b] и имеет непрерывные частные производные
fy и uf по второму и третьему аргументам на промежутке (a, b),
то в окрестности любой точки x0 (a, b) существует и притом единственное решение уравнения (1.2), удовлетворяющее начальным условиям (1.4).
Второй способ нахождения частного решения уравнения (1.2) состоит в задании так называемых краевых (граничных) условий. В отличие от начальных условий (1.4), задаваемых в одной (начальной) точке x0, краевые условия для нахождения конкретных значений постоянных c1 и c2 задаются в двух различных (граничных) точках промежутка (a, b). В этом случае решение уравнения (1.2) ищется внутри промежутка (a, b).
К примеру, простейшие двухточечные краевые условия для уравнения (1.2) имеют вид
y(a) = A, y(b) = B, |
(1.5) |
где A и B – заданные числа. При A = B = 0 краевые условия (1.5) называются однородными.
Краевая задача (1.2), (1.5) в этом случае состоит в нахождении решения уравнения (1.2), проходящего через две точки M1(a, A) и
M2(b, B).
11
elib.pstu.ru
Краевая задача (1.2), (1.5) может:
1)иметь единственное решение;
2)не иметь ни одного решения;
3)иметь множество решений.
Примеры решения простейших краевых задач для обыкновенных дифференциальных уравнений будут приведены ниже.
1.2. Структура общего решения линейного дифференциального уравнения второго порядка
Уравнение (1.2) в общем случае нелинейно. Линейное дифференциальное уравнение второго порядка может быть записано в следующем виде:
y′′(x) + a1(x) y′(x) + a2(x) y(x) = f (x). |
(1.6) |
Здесь f(x) и коэффициенты a1(x), a2(x) – заданные на промежутке (a, b) функции. Часто предполагается, что функции f(x), a1(x) и
a2(x) непрерывны.
При f(x) ≡ 0 уравнение (1.6) принимает вид
y′′(x) + a1(x) y′(x) + a2(x) y(x) = 0 |
(1.7) |
и называется однородным.
Известно, что для нахождения общего решения однородного уравнения (1.7) достаточно найти два линейно независимых решения y1(x) и y2(x) этого уравнения. Тогда общее решение уравнения (1.7) может быть представлено в виде
y = c1 y1(x) + c2 y2(x), |
(1.8) |
где c1 и c2 – произвольные постоянные.
Для нахождения общего решения неоднородного уравнения (1.6), то есть уравнения с отличной от нуля правой частью f(x), необходимо сначала найти общее решение соответствующего однородного уравнения и дополнительно найти какое-либо частное решение y*(x) исходного неоднородного уравнения. Тогда общее решение неоднородного уравнения (1.6) запишется в виде
12
elib.pstu.ru
y = c1 y1(x) + c2 y2(x) + y*(x). |
(1.9) |
Примеры отыскания решений линейных дифференциальных уравнений, в том числе с начальными условиями, можно найти в учебниках и учебных пособиях по высшей математике.
Приведем примеры решения двухточечных краевых задач вида (1.7), (1.5). Нас прежде всего будут интересовать однородные краевые задачи, то есть задачи отыскания решений однородных линейных дифференциальных уравнений с однородными краевыми условиями.
1.3. Постановка простейшей задачи Штурма–Лиувилля на собственные значения
Рассмотрим следующую однородную краевую задачу: |
|
y′′(x) + μ y(x) = 0. |
(1.10) |
y(a) = 0, y(b) = 0. |
(1.11) |
Отметим, что уравнение (1.10) содержит свободный параметр μ, который может принимать любые действительные значения. Очевидно, что в силу однородности уравнения (1.10) и краевых условий (1.11) при любых значениях параметра μ R эта задача имеет тривиальное (нулевое) решение y(x) ≡ 0. Но это решение может быть не единственным.
Оказывается, что при некоторых значениях параметра μ задача (1.10)–(1.11) может иметь вторые, отличные от тождественного нуля решения.
Дадим следующие определения.
Значения параметра μ, при которых задача (1.10)–(1.11) имеет нетривиальное решение, называются собственными значениями этой краевой задачи, а соответствующие этим значениям (ненулевые) решения называются собственными функциями задачи (1.10)–(1.11).
Рассматриваемая задача о поиске собственных значений и собственных функций уравнения (1.10) с краевыми условиями (1.11) – это частный случай так называемой задачи Штурма–Лиувилля –
13
elib.pstu.ru
задачи об отыскании собственных значений и собственных функций однородной краевой задачи для обыкновенного линейного дифференциального уравнения второго порядка с самосопряженным оператором, действующим в пространстве функций L2[[a, b], интегрируемых с квадратом на промежутке [a, b].
Пример. Рассмотрим следующую краевую задачу Штурма– Лиувилля (1.10) на промежутке [0, l]:
y′′(x) + μ y(x) = 0, |
|
y(0) = 0, y(l) = 0. |
(1.12) |
Требуется найти собственные значения и собственные функ- |
|
ции этой задачи. |
|
Рассмотрим три случая. |
|
1. Пусть μ = 0. Тогда уравнение (1.10) принимает следующий |
|
вид: |
|
y′′(x) = 0. |
(1.13) |
Общее решение этого уравнения имеет вид |
|
y = c1 x + c2. |
(1.14) |
Значения произвольных постоянных c1 и c2 находим из краевых условий (1.12). Получаем, что y(0) = 0 = c2, y(l) = 0 = c1. Подставляя найденные значения c1 = c2 = 0 в равенство (1.14), получаем, что при α = 0 задача (1.13)–(1.12) имеет единственное тривиальное решение y(x) ≡ 0.
2. Пусть параметр μ принимает отрицательные значения: μ = −λ2, R. Тогда уравнение (1.10) принимает следующий вид:
|
y′′(x) − λ2y(x) = 0. |
(1.15) |
|
Соответствующее |
ему |
характеристическое |
уравнение |
k2−λ2 ≡ (k − λ)(k + λ) = 0 имеет два различных действительных корня k1 = λ и k2 = −λ, которым соответствуют два линейно независимых частных решения уравнения (1.15): y1 = eλx и y2 = e−λx. Согласно теореме о структуре общего решения (см. формулу (1.8)) общее решение уравнения (1.15) имеет следующий вид:
14
elib.pstu.ru
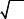
y = c1 eλx + c2 e−λx. |
(1.16) |
Из краевых условий получаем следующую однородную систему линейных алгебраических уравнений для нахождения постоянных c1 и c2:
c |
c |
|
0, |
|
|
|
1 |
2 |
|
(1.17) |
|
|
|
|
c e l 0. |
||
c e l |
|
||||
|
1 |
|
|
2 |
|
Очевидно, эта система имеет тривиальное решение c1 = c2 = 0, и это решение единственно, так как главный определитель системы (1.17) отличен от нуля: = e−λl+eλl ≠ 0. Поэтому нулевое решение y(x) ≡ 0 краевой задачи (1.15), (1.12) также является единствен-
ным. |
|
|
|
3. Пусть параметр |
μ принимает положительные |
значения: |
|
μ = λ2, λ R. Тогда уравнение (1.10) принимает следующий вид: |
|||
|
y1 = cos(λx) и y2 = sin(λx) |
(1.18) |
|
Соответствующее |
ему |
характеристическое |
уравнение |
k2+λ2 ≡ (k − λi)(k + λi) = 0 имеет два различных чисто мнимых корня k1 = λi и k2 = −λi (здесь i = 1 – мнимая единица). Этим корням со-
ответствуют два линейно независимых частных решения уравнения
(1.18): y1 = cos(λx) и y2 = sin(λx).
Согласно теореме о структуре общего решения (см формулу
(1.8)) общее решение уравнения (1.15) имеет следующий вид: |
|
y = c1 cos(λx) + c2 sin(λx). |
(1.19) |
Из краевых условий получаем следующую линейную однородную систему алгебраических уравнений для нахождения постоянных c1 и c2:
c |
0, |
(1.20) |
1 |
|
|
c2 sin l 0. |
|
|
Очевидно, эта система имеет нулевое решение c1 = c2 = 0, которое нам неинтересно, так как снова приводит к тривиальному реше-
нию y(x) ≡ 0 краевой задачи (1.18), (1.12).
15
elib.pstu.ru
Но нетрудно заметить, что если значения параметра λ обращают уравнение
sin(λl) = 0 |
(1.21) |
в тождество, то система (1.20) имеет ненулевые решения, то есть постоянная c2 может быть отличной от нуля (c1 = 0, c2 ≠ 0).
Тригонометрическому уравнению (1.21) удовлетворяет счетное множество значений
|
|
|
|
λn= |
n |
, n = 0, ±1, ±2,… |
(1.22) |
|
|
|
|
|
l |
|
|
2 |
|
n 2 |
|
|
|
||
Числа n = n |
= |
l |
|
называются собственными значениями |
|||
|
|
|
|
|
|
|
|
краевой задачи (1.18), (1.12) Штурма–Лиувилля.
Каждому из значений λn при n = 1, 2,… соответствует своя ненулевая собственная функция
yn(x) = sin λnx = sin |
n x, n = 1, 2,… , |
(1.23) |
|
l |
|
которая, как следует из формулы (1.19), является ненулевым реше-
нием задачи (1.18), (1.12).
Нетрудно заметить, что так как краевая задача (1.18), (1.12) является однородной, то и любая конечная линейная комбинация собственных функций yn(x)
An yn (x) = An sin n x |
(1.24) |
|
n 1 |
n 1 |
|
с любыми числовыми коэффициентами An удовлетворяет и уравнению (1.18), и краевым условиям (1.12), то есть конечная сумма
An sin n x также является решением краевой задачи Штурма–
n 1
Лиувилля (1.18), (1.12) при любых значениях коэффициентов An.
16
elib.pstu.ru
Если же сумма An sin n x содержит бесконечное число сла-
n 1
гаемых, то она представляет собой ряд An sin n x , который явля-
n 1 |
|
|
ется рядом Фурье по системе sin( n x) |
|
взаимно- |
n 1 |
ортогональных собственных функций задачи Штурма–Лиувилля. Если этот ряд сходится к некоторой функции y(x), то сумма этого ряда также является ненулевым решением краевой задачи Штурма– Лиувилля (1.18)–(1.12).
Однако условия сходимости ряда (1.25) налагают определенные ограничения на значения коэффициентов An. Из теории рядов Фурье известно, что если этот ряд сходится к некоторой функции y(x):
|
|
|
|
|
y(x) = An sin n x , |
(1.25) |
|||
|
|
n 1 |
|
|
то коэффициенты An этого ряда выражаются по формулам |
|
|||
|
2 |
l |
|
|
An = |
l |
0 |
y(x)sin n xdx |
(1.26) |
|
|
|||
и называются коэффициентами Фурье.
Напомним, что достаточные условия разложимости функции y(x) в ряд Фурье на промежутке [0, l] состоят в требованиях кусочной непрерывности и кусочной дифференцируемости этой функции.
Контрольные вопросы
1.Дайте определение обыкновенного дифференциального уравнения n-го порядка.
2.Запишите общий вид обыкновенного дифференциального уравнения второго порядка, разрешенного относительно старшей производной. Дайте определение решения и общего решения этого уравнения.
17
elib.pstu.ru
3.Поставьте задачу Коши для дифференциального уравнения второго порядка, разрешенного относительно старшей производной, и сформулируйте теорему существования и единственности решения этой задачи.
4.Дайте определение линейного обыкновенного дифференциального уравнения второго порядка.
5.Сформулируйте теоремы о структуре общего решения линейного однородного и неоднородного дифференциального уравнения второго порядка.
6.Приведите пример решения краевой задачи для обыкновенного дифференциального уравнения второго порядка.
7.Приведите пример решения задачи Штурма–Лиувилля на собственные значения.
8.Что такое ряд Фурье? Укажите необходимые и достаточные условия разложимости некоторой функции y(x) в ряд Фурье.
18
elib.pstu.ru
2.ПОНЯТИЕ УРАВНЕНИЙ
ВЧАСТНЫХ ПРОИЗВОДНЫХ
Вотличие от обыкновенных дифференциальных уравнений, уравнения в частных производных содержат не одну, а две или более свободных переменных, от которых зависит искомая функция. Порядок уравнения определяет, как и ранее, порядок старшей производной.
2.1.Дифференциальные уравнения
вчастных производных первого порядка
Вобщем виде дифференциальное уравнение первого порядка с частными производными относительно неизвестной функции двух переменных u(x, y) может быть записано в следующей форме:
F (x, y, u(x, y), |
u(x, y) |
, |
u(x, y) |
) = 0. |
(2.1) |
|
x |
|
y |
|
|
Здесь F – это заданная функция пяти переменных (x, y, u, v, w); x и y – независимые переменные; u(x,y) – искомая функция этих перемен-
ных, u(x, y) и u(x, y) – частные производные искомой функции.
x y
Если функция F линейна, то уравнение (2.1) называется линейным. Линейное дифференциальное уравнение в частных производных первого порядка относительно функции u(x,y) двух независи-
мых переменных может быть записано в следующей форме:
a1(x,y) |
u(x, y) |
+ a2(x,y) |
u(x, y) |
+ a3(x,y) u(x, y) = f((x, y). (2.2) |
|
x |
y |
||||
|
|
|
Здесь f((x, y) и коэффициенты a1(x,y), a2(x,y), a3(x,y) – заданные функции двух переменных, причем хотя бы один из коэффициентов a1(x,y) или a2(x,y) отличен от тождественного нуля. Часто предполагается, что функции f((x, y), a1(x,y), a2(x,y) и a3(x,y) непрерывны в
19
elib.pstu.ru

некоторой двумерной области D. В целях компактности записи в теории уравнений с частными производными принято обозначать
частные производные следующим образом: u(x, y) = ux, u(x, y) = uy.
x y
Решение уравнения вида (2.1) в частных производных – дифференцируемая функция u(x,y), обращающая это уравнение в тождество.
Напомним, что дифференцируемость функции двух переменных u(x,y) означает существование полного дифференциала du
функции u(x, y): du = u(x, y) dx + u(x, y) dy ≡ uxdx + uydy. |
|
|
x |
y |
|
Приведем пример решения дифференциального уравнения |
||
первого порядка с частными производными. |
|
|
Пример 2.1. Решить уравнение |
|
|
u(x, y) |
− u(x, y) = 0, |
(2.3) |
x |
|
|
Решение. Разделим переменные: |
|
|
u(x, y) |
= x |
|
u(x, y) |
|
|
и найдем частные интегралы по переменной x от левой и правой частей последнего равенства. Получим равенство ln u(x, y) = x + c(y), откуда
u(x, y) = ec( y) ex ≡ c1(y) ex, |
(2.4) |
где c1(y) – произвольная функция переменной y.
Обратим внимание на то, что полученное решение u(x,y) уравнения первого порядка с частными производными – это общее решение и найти его удается с точностью до произвольного множителя – функции c1(y).
Для проверки правильности решения можно подставить найденное решение u(x, y) = c1(y)ex в исходное уравнение (2.3) и полу-
20
elib.pstu.ru
