ТЕРВЕР 1

Однородные Марковские процессы.

1. Пусть {E₁, E₂, E₃} – возможные состояния системы и P – матрица вероятностей перехода из состояния в состояние за один шаг:

Построить граф, соответствующий матрице Р.

2. На окружности расположены шесть точек E₁, E₂, E₃, E₄, E₅, E₆ равноотстоящих друг от друга. Частица движется из точки в точку следующим образом. Из данной точки она перемещается в одну из ближайших соседних точек с вероятностью ¼ или в диаметрально противоположную точку с вероятностью ½. выписать матрицу вероятностей перехода для этого процесса и построить граф соответствующий этой схеме.

Ответ:

3. Погода на некотором острове через длительные периоды времени становится то дождливой (Д), то сухой (С). Вероятности ежедневных изменений заданы матрицей:

I	II

а) Если во вторник погода дождливая, то какова вероятность, что она будет дождливой в ближайший четверг?

б) если во вторник ожидается дождливая погода с вероятностью 0,3 (0,8), то какова вероятность, что она будет дождливой в ближайший четверг?

Ответ: I а) 0,61; б) 0,547; II - ?

4. Электрон может находиться на одной из счетного множества орбит в зависимости от наличной энергии. Переход с i-той орбиты на j-тую происходит за 1 секунду с вероятностью

Найти: а) вероятность перехода за 2 секунды

б) постоянную с_i

Ответ: а)

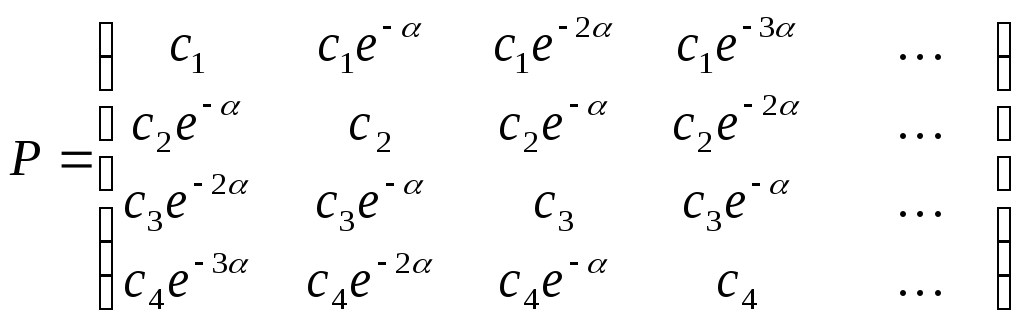
б)

Замечание: здесь рассматривается физический процесс с бесконечным (счетным) множеством состояний.

5. Рассмотрим Марковскую цепь с двумя состояниями S₁ и S₂ и матрицей вероятностей перехода.

. С помощью особого устройства случайного выбора выбирают состояние, с которого начинается процесс. Это устройство выбирает S₁ с вероятностью ½ и S₂ с вероятностью ½.

Требуется: а) найти вероятность того, что после первого шага этот процесс перейдет в состояние S₁.

б) то же самое для случая, когда устройство выбирает S₁ с вероятностью ¼ и S₂ с вероятностью ¾.

Ответ:

6. В учениях участвуют два корабля, которые одновременно производят выстрелы друг в друга через равные промежутки времени. При каждом обмене выстрелами корабль А поражает корабль В с вероятностью ½, а корабль В поражает корабль А с вероятностью 3/8. Предполагается, что при любом попадании корабль выходит из строя. Рассматриваются результаты серии выстрелов. найти матрицу вероятностей перехода, если состояниями цепи являются комбинации кораблей, оставшихся в строю: S₁ – оба корабля в строю, S₂ – в строю корабль А, S₃ – в строю корабль В, S₄ – оба корабля поражены.

Ответ:

7. Матрица вероятностей перехода цепи Маркова имеет вид

а) , б)

Распределение по состояниям в момент времени t=0 определяется вектором: а) (0.7; 0.2;0;1) б) (0; 0; 0; 1)

Найти:

1. распределение по состояниям в момент t=2;

2. вероятность того, что в моменты t=0; 1; 2; 3 состояниями цепи будут соответственно S₁, S₂, S₃, S₄;

3. стационарное распределение

Ответ: 1) (0.385; 0.336; 0.279); 2) 0.3366; 3) (16.47; 17.47; 14.47)

Указание: Найти P²

8. Даны вектор начальных вероятностей (a₁, a₂, …, a_r) и переходные вероятности p_ij (i,j=1, 2, …, r) цепи Маркова. Найти вероятность того, что в моменты времени n₁, n₂, …, n_s состояниями цепи будут соответственно S_i1, S_i2, …, S_in.

Здесь моменты времени не обязательно являются соседними.

Ответ:

9. Доказать, что если для пи Маркова с матрицей вероятностей перехода (p_ij) в качестве вектора начальных вероятностей взять предельные вероятности (b₁, b₂, …, b_n), то этот вектор не будет изменяться со временем.

10. В некоторой местности климат весьма изменчив. Здесь никогда не бывает двух одинаковых ясных дней подряд. Если сегодня ясно, то завтра с одинаковой вероятностью пойдет дождь или снег. Если сегодня снег (или дождь), то с вероятность ½ погода не измениться. Если все же она измениться, то в половине случаев снег заменяется дождем или наоборот и лишь в половине случаев на следующий день будет ясная погода.

Требуется:

а) принимая в качестве состояний цепи различные виды погоды Д, Я, С выписать матрицу Р вероятностей перехода;

б) построить граф, соответствующий матрице Р;

в) определить вероятность хорошей погоды через три дня после дождя.

г) найти предельные вероятности.

Ответ: а)

б)

в) 13/64

г) (0; 4; 0.2; 0.4)

12. Матрица вероятностей перехода

, 1

Определить вероятности перехода p_ij и средние предельные вероятности перехода , i,j=1,2,3,4.