Решение геометрических и физических задач с помощью определенного ин

Вариант 29

1. Вычислить площадь фигуры, ограниченной графиками функций, заданных в прямоугольных координатах:

y = x2 + x; y = x +1.

2. Вычислить площадь фигуры, ограниченной линиями, заданными следующими параметрическими уравнениями:

3.Вычислить площадь фигуры, ограниченной линией, заданной в полярных координатах уравнением

ρ= 2 +cos ϕ.

4.Вычислить длину дуги кривой, заданной в прямоугольных координатах уравнением

5. Вычислить длину дуги кривой, заданной параметрически: x =5(sin t −t cost); y =5(cost −t sin t); 0 ≤t ≤ 2π.

6. Вычислить длину дуги кривой, заданной в полярных координатах уравнением

51

7. Вычислить объем тела, ограниченного поверхностями, заданными уравнениями:

4x2 +9 y2 −36z2 =36; z = 0; z =3.

8. Вычислить объем тела, образованного вращением вокруг оси Ох областей, ограниченных графиками заданных функций:

y2 = x −2; y = x3; y = 0; y =1.

9.Найти площадь поверхности, образованной вращением вокруг оси Ох петли кривой 9x2 = x(3 − x)2.

10.Найти центр тяжести тела, образованного вращением во-

круг оси Оу фигуры, ограниченной гиперболой x2 − y2 =1 и пря- 1 1

мыми y = 0 и y =1.

11. Треугольная пластинка, основание которой a, а высота h, вращается вокруг основания с постоянной угловой скоростью ω. Найти кинетическую энергию пластинки, если толщина ее равна d, а плотность материала, из которого она изготовлена, равна γ. Кинетическая энергия тела вращения вокруг неподвижной оси равна 0,5Jω2 , где ω – угловая скорость, а J – момент инерции относительно оси вращения.

Вариант 30

1. Вычислить площадь фигуры, ограниченной графиками функций, заданных в прямоугольных координатах:

y = x2 −4; x − y +2 = 0.

52

2. Вычислить площадь фигуры, ограниченной линиями, заданными следующими параметрическими уравнениями:

x =3(2cost −cos 2t); y =3(2sin t −sin 2t).

3.Вычислить площадь фигуры, ограниченной линией, заданной в полярных координатах уравнением

ρ=3(1+cos ϕ).

4.Вычислить длину дуги кривой, заданной в прямоугольных координатах уравнением

y = −e−x ; ln 3 ≤ x ≤ ln 8.

5. Вычислить длину дуги кривой, заданной параметрически:

x =sin3 t; y =cos3 t; 0 ≤t ≤ π.

6.Вычислить длину дуги кривой, заданной в полярных координатах уравнением

ρ=sec ϕ; 0 ≤ϕ≤ π4 .

7.Вычислить объем тела, ограниченного поверхностями, заданными уравнениями:

8. Вычислить объем тела, образованного вращением вокруг оси Ох областей, ограниченных графиками заданных функций:

y = x3; y = x2.

53

9.Найти площадь поверхности, образованной вращением вокруг оси Ох петли кривой 8y2 = x2 −4x4.

10.Найти центр тяжести плоского тела, ограниченного лежащей в первом квадранте четвертью эллипса, заданного уравнением

x2 + y2 =1. 22 32

11. Идеальный газ, заключенный в цилиндрический сосуд, закрытый подвижным поршнем, расширяясь, увеличивается в объеме, передвигая при этом поршень. Найти работу, совершаемую силой давления газа, если объем увеличивается от ν0 до ν1, а темпе-

ратура не изменяется.

54

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1.Высшая математика в упражнениях и задачах с решениями: учеб. пособие для вузов: в 2 ч. / П.Е. Данко [и др.]. – 6-е изд. – М.: Оникс: Мир и Образование, 2006. – Ч. 1. – 304 с.

2.Задачи и упражнения по математическому анализу для втузов: учеб. пособие для втузов / Г.С. Бараненков [и др.]; под ред. Б.П. Демидовича. – М.: Астрель: АСТ, 2010. – 495 с.

3.Шипачев В.С. Высшая математика: учеб. для вузов. – 9-е изд., стер. – М.: Высшая школа, 2008. – 479 с.

4.Берман Г.Н. Сборник задач по курсу математического анализа: учеб. пособие. – 22-е изд., перераб. – СПб.: Профессия, 2001. – 432 с.

5.Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов: в 2 т. – М.: Интеграл-Пресс, 2010. – Т. 1. – 415 с.

6.Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика: учеб. пособие для вузов. – 3-е изд., испр. – М.: Физмат-

лит, 2006. – 368 с.

55

ПРИЛОЖЕНИЕ

Вариант решения контрольных заданий

1. Вычислить площадь фигуры, ограниченной параболой y = 2 − x2 и кривой y3 = x2 (рис. 1).

Рис. 1

Решение.

Решая совместно систему уравнений

=2 − 13 − 53 − −2 + 13 + 53 = 2152 .

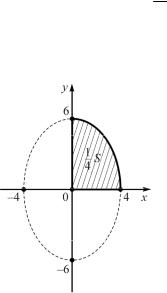
2.Найти площадь эллипса, используя его параметрические

уравнения (рис. 2): х = 4cos t, y =6sin t.

Рис. 2

Решение.

Ввиду симметрии достаточно вычислить площадь одной чет-

S = 6π 4 = 24π.

57

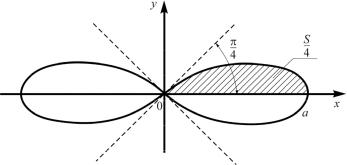
3. Найти площадь фигуры, заключенной внутри лемнискаты Бернулли ρ2 = a2 cos 2ϕ (рис. 3).

Рис. 3

Решение.

В силу симметрии кривой определяем сначала одну четверть искомой площади. Найдем пределы интегрирования по ϕ. При

динатах (рис. 4).

58

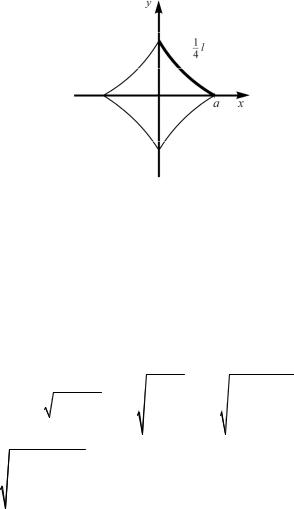
Рис. 4

Решение.

Дифференцируя уравнение астроиды, получим:

Поэтому для длины одной четверти астроиды имеем:

Решение.

Найдем производные по параметру t: x′(t ) = −5cos4 t sin t, y′(t ) =5sin4 t cost.

Отсюда:

π

2

=5∫ cos t sin t sin6 t +cos6 tdt.

0

Преобразуем выражение под корнем:

sin6 t +cos6 t =(1−cos2 t )3 +cos6 t =

=1−3cos2 t +3cos4 t −cos6 t +cos6 t =

=1−3cos2 t +3cos4 t =1+3cos2 t (cos2 t −1) =

=1−3cos2 t sin2 t =1− 34 sin2 2t =

=1− 34 (1−cos2 2t ) = 14 + 34 cos2 2t.

Получим: