
Приложения определенного интеграла учебно-методическое пособие
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
М.А. Макагонова, И.В. Тонкоева
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Утверждено Редакционно-издательским советом университета
в качестве учебно-методического пособия
Издательство Пермского национального исследовательского
политехнического университета
2014
УДК 517.38(072.8) М15
Рецензенты:
канд. физ.-мат. наук, доцент Ю.Н. Еленский (Пермский государственный национальный исследовательский университет); старший преподаватель Н.В. Рогова (Пермский национальный исследовательский политехнический университет)
Макагонова, М.А.
М15 Приложения определенного интеграла : учеб.-метод. пособие / М.А. Макагонова, И.В.Тонкоева. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2014. – 33 с.
ISBN 978-5-398-01258-3
Рассмотрено использование определенного интеграла при решении геометрических и физических задач, приведены примеры их решения.
Предназначено для студентов всех направлений подготовки дневного и заочного отделений.
УДК 517.38(072.8)
ISBN 978-5-398-01258-3 |
© ПНИПУ, 2014 |
2
ОГЛАВЛЕНИЕ |
|
1. Геометрические приложения определенного интеграла...... |
4 |
1.1. Площадь криволинейной трапеции................................ |
4 |
1.1.1. Площадь трапеции, ограниченной кривыми, |
|
заданными в декартовой системе координат ................. |
4 |
1.1.2. Площадь трапеции, ограниченной кривой, |
|
заданной параметрически............................................. |
7 |
1.1.3. Площадь криволинейного сектора...................... |
8 |
1.2. Длина дуги кривой......................................................... |
10 |
1.2.1. Длина дуги кривой, заданной в декартовой |
|
системе координат ...................................................... |
10 |
1.2.2. Длина дуги кривой, заданной в параметрическом |
|
виде.............................................................................. |
11 |
1.2.3. Длина дуги кривой, заданной в полярных |
|
координатах................................................................. |
12 |
1.3. Объем тела..................................................................... |
13 |
1.3.1. Вычисление объема тела по площадям |
|
параллельных сечений ................................................. |
13 |
1.3.2. Объем тела вращения.......................................... |
15 |
1.4. Площадь поверхности вращения.................................... |
21 |
2. Физические приложения определенного интеграла............. |
23 |
2.1. Работа переменной силы................................................ |
23 |
2.2. Путь, пройденный точкой.............................................. |
26 |
2.3. Статические моменты и моменты инерции |
|
плоских дуг и фигур............................................................. |
26 |
2.4. Координаты центра тяжести. Теоремы Гульдена........... |
29 |
Список рекомендуемой литературы ......................................... |
31 |
3
1. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
При решении геометрических задач определенный интеграл используется для определения площадей криволинейных фигур, длины дуги кривой, объема тела, площади поверхности вращения.
1.1.Площадь криволинейной трапеции
1.1.1.Площадь трапеции, ограниченной кривыми, заданными в декартовой системе координат
Пусть на плоскости Оху дана фигура, ограниченная отрезком [a, b] оси Ох, прямыми x = a, x = b и графиком непрерывной и не-
отрицательной функции y = f (x) на [a, b]. |
Это криволинейная тра- |
пеция. Тогда площадь S этой трапеции может быть вычислена по |
|
следующей формуле: |
|
b |
|
S = ∫ f (x)dx. |
(1) |
а
Рис. 1
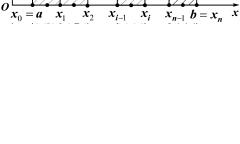
Докажем это. Разобьем произвольно отрезок [a, b] на n частей точками: a = x0 < x1 < x2 < ... < xi−1 < xi < ... < xn = b, выберем на каж-
4
дом частичном отрезке [xi−1, xi ] произвольную точку ti (xi−1 ≤ti ≤ xi )
и рассмотрим ступенчатую фигуру (рис. 1). Площадь S криволинейной трапеции приближенно равна площади этой ступенчатой фигу-
n |
∆xi = xi − xi−1. При λ = max{∆xi} →0 пло- |
ры: S ≈ ∑ f (ti ) ∆xi , где |
|
i=1 |
1≤i≤n |
|
щадь ступенчатой фигуры стремится к площади криволинейной трапеции.
С другой стороны, площадь ступенчатой фигуры является интегральной суммой для интеграла (1). Поскольку функция f ( x) не-
прерывна на [a,b], то предел этой суммы при λ = max{∆xi} →0 су-
1≤i≤n
ществует и равен интегралу от функции f ( x) по [a,b]. Следовательно, и площадь S криволинейной трапеции численно равна
определенному интегралу от функции |
f ( x) по [a,b]: |
n |
b |
S = lim ∑ f (t1 ) ∆xi |
= ∫ f ( x)dx. |
λ→0 i=1 |
а |
Таким образом, геометрический смысл определенного интеграла состоит в том, что определенный интеграл от неотрицательной непрерывной функции f ( x) по [a,b] численно равен площади кри-
волинейной трапеции с основанием [a,b] , ограниченной сверху графиком функции y = f ( x).
Рассмотрим другой случай. Пусть фигура ограничена снизу
и сверху графиками функций y = f1 ( x) |
и y = f2 (x), при этом |
f1 ( x) ≤ f2 (x), a ≤ x ≤b и f1 ( x), f2 (x) |
– непрерывные функции. |
Если обе функции неотрицательны, то площадь S данной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций y = f2 (x) и y = f1 ( x)
(рис. 2).
5
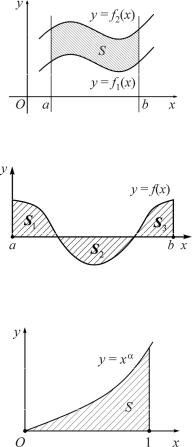
Рис. 2
Рис. 3
Рис. 4
По формуле (1) имеем:
Следовательно,
S= ∫b f2 (x)dx −∫b f1 (x)dx =
аа
= ∫b [ f2 (x) − f1(x)]dx. |
(2) |
а |
|
Формула (2) справедлива и тогда, когда f1 (x) и f2 (x) не являют-
ся неотрицательными.
В общем случае, когда функция y = f (x) на [a,b] принимает значе-
ния разных знаков, определенный интеграл выражает разность площадей криволинейных трапеций, расположенных над осью Ох и под ней (рис. 3), так как площадям криволинейных трапеций, расположенных под осью Ох, присваивается знак
«–», т.е. ∫b f ( x)dx = S1 −S2 + S3.
а
Пример 1
Найти площадь фигуры, ограниченной графиком функции
y = xα, α > 0, прямой x =1 и осью
Ох (рис. 4).
|
|
|
|
1 |
|
x |
α+1 |
|
|
1 = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
S = ∫ xαdx = |
|
|
|
. |
|
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
0 |
|
α+1 |
|
0 |
α+1 |
|
|||
|
|
|
|
|
|
|
|||||||
Если α =1, |
то |
S = |
1 |
; |
если α = 2, |
|
|
то |
S = 1 |
и т.д. |
|||
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
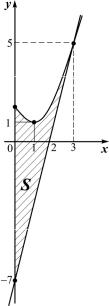
Пример 2
Найти площадь фигуры, ограниченной графиками функций y = x2 −2x +2, y = 4x −7 , осью Оу (рис. 5).
Найдем абсциссы точек пересечения прямой
y = 4x −7 с параболой |
|
y = x2 −2x +2 . Для этого |
|
решим систему уравнений: |
|||
|
у = 4х−7, |
||
|
у = х |
2 |
−2х+2. |
|
|
||
Получим: x =3 ( y =5).
Поскольку ветви параболы направлены вверх, то парабола лежит над прямой на отрезке [0;3]. По формуле (2) находим:
3 |
|
|
|
|
|
|
3 |
S = ∫ x2 −2x +2 −(4x −7) dx = ∫(x2 −6x +9)dx = |
|||||||
0 |
|
|
|
|
|
|
0 |
|
х |
3 |
−3х2 |
|
|
|
|
|
3 |
|
|||||
= |
|
+9 |
х |
|
=9. |
||
3 |
|
||||||
|
|
|
|
0 |
|
||
Рис. 5
1.1.2. Площадь трапеции, ограниченной кривой, заданной параметрически
Пусть криволинейная трапеция ограничена кривой, заданной в параметрическом виде: x = x(t ), y = y (t ), t [α,β], прямыми x = a,
x =b и осью Ох. |
|
|
|
|
|
В формуле (1) надо |
сделать замену переменной, |
положив |
|||
x = x(t ), dx = x′(t )dt, причем x(α) = a, x(β) =b, тогда |
|
||||
S = |
|
β∫ y (t ) x′(t )dt |
|
. |
(3) |
|
|
||||
|
|
α |
|
|
|
|
7 |
|
|
|
|

Пример 3
Вычислить площадь фигуры, ограниченной эллипсом, заданным уравнениями x = a cost, y =bsin t, 0 ≤t ≤ 2π.
Эллипс симметричен относительно осей координат (рис. 6), поэтому достаточно вычислить площадь части фигуры, находящейся в 1-й четверти.
Следовательно, по формуле (3) получим:
Рис. 6
0
S = 4∫ bsin t
π
2
π |
π |
|
2 |
2 |
(1−cos 2t )dt = |
(a cost )′dt = 4аb∫ sin2 tdt = 2аb∫ |
||
0 |
0 |
|
|
1 |
|
π |
= πаb. |
= 2аb t − |
2 |
sin 2t |
2 |
|
|
|
0 |
|
Здесь х изменяется от 0 до а, следовательно, t изменяется от π2
до 0.
1.1.3. Площадь криволинейного сектора
Пусть кривая АВ задана в полярных
координатах уравнением |
ρ =ρ(ϕ), |
|||
α ≤ ϕ≤β, |
причем функция ρ(ϕ) |
непре- |
||
рывна |
и |
неотрицательна |
на |
отрезке |
[α,β] . |
Плоскую фигуру, ограниченную |
|||
кривой АВ и двумя лучами, составляющими с полярной осью углы α и β, бу- Рис. 7 дем называть криволинейным сектором (рис. 7). Площадь криволинейного сектора
8
|
S = 1 |
∫β ρ2 (ϕ)dϕ. |
|
(4) |
||
|
|
2 |
α |
|
|
|
|
|
|
|
|
|
|
Докажем это. Разобьем произвольно отрезок [α,β] |
на n частей |
|||||
точками: α = ϕ0 < ϕ1 < ϕ2 <... < ϕi−1 < ϕi <... < ϕn |
=β, выберем на каж- |
|||||
дом частичном |
отрезке |
[ϕi−1,ϕi ] |
произвольную |
точку ξi |
||
(ϕi−1 ≤ξi ≤ ϕi ) и |
построим |
круговые |
сектора |
с радиусами ρ(ξi ). |
||
Получим веерообразную фигуру (см. рис. 7), площадь которой приближенно равна площади S криволинейного сектора:
S = |
1 ∑ρ2 |
(ξi ) ∆ϕi , |
|
n |
|
|
2 i=1 |
|
где ∆ϕi = ϕi −ϕi−1.
С другой стороны, площадь веерообразной фигуры является интегральной суммой для интеграла (4). Поскольку функция ρ2 (ϕ) непрерывна на отрезке [α,β], то предел этой суммы при
λ = max{∆ϕi} →0 существует и равен интегралу (4). Следовательно,
1≤i≤n
и площадь криволинейного сектора численно равна этому определенному интегралу:
|
1 lim |
n |
(ξi )∆ϕi = |
1 |
β |
|
(ϕ)dϕ. |
|
S = |
∑ρ2 |
α∫ |
ρ2 |
|||||
|
2 |
λ→0 i=1 |
|
2 |
|
|
||
Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, а затем к ним применить полученную формулу для нахождения площади.
Пример 4
Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, заданной уравнением ρ = аϕ, где
а > 0 (рис. 8). При изменении ϕ от 0 до 2π полярный радиус опи-
9

сывает кривую, ограничивающую криволинейный сектор ОАВС. Поэтому по формуле (4) имеем:
|
SОАВС = |
a2 2π |
2 |
dϕ= |
a2 |
|
ϕ3 |
|
π |
= |
|||
|
2 |
||||||||||||
|
2 |
∫ |
ϕ |
2 |
3 |
0 |
|||||||
|
|
0 |
|
|
|
|
|
|
|||||
Рис. 8 |
= a2 |
8π3 |
= |
4 |
π3a2. |
|
|
|
|||||
|
2 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
1.2.Длина дуги кривой
1.2.1.Длина дуги кривой, заданной в декартовой системе
координат
Пусть плоская кривая АВ задана уравнением y = f (x), a ≤ x ≤b, где f (x) – непрерывная функция на отрезке [a,b]. Разо-
бьем кривую АВ на n произвольных частей точками A = M0 , M1, M2 ,..., Mi−1, Mi ,..., Mn = B в направлении от А к В. Соединив соседние точки хордами, получим некоторую вписанную в кривую АВ ломаную, длину которой обозначим через Р (рис. 9). Пусть li – длина одного звена Mi−1Mi ломаной, а µ = max{li}.
Рис. 9
Если существует предел L длин P (L = limµ→0 P) вписанных в кри-
вую ломаных при µ →0, то этот предел называется длиной дуги АВ.
10
