Термохимия

В термодинамических таблицах приведены значения стандартной энергии Гиббса . Значения для элементов приняты равными нулю.

Значения получают экспериментально, проводя соответствующую реакцию в лабораторных условиях. Наиболее точно они определяются по ЭДС гальванического элемента в связи с тем, что в гальваническом элементе можно проводить химическую реакцию практически обратимо, т.е. получать максимальное значение полезной работы .

Максимальная полезная работа связана с электродвижущей силой гальванического элемента уравнением:

,

где n  число молей электронов, приходящееся на один моль прореагировавшего вещества и протекших через внешнюю цепь при стандартных условиях; F = = 9,6510⁷ Кл/кмоль  постоянная Фарадея,  электродвижущая сила. Измеряя ЭДС, получают значение энергии Гиббса.

Замечания. 1) ЭДС представляет собой максимальное значение напряжения гальванического элемента, соответствующее обратимому протеканию химической реакции.

2) Получаемое значение относится к тому веществу, которое является продуктом реакции в данном гальваническом элементе с определенным (щелочным или кислым) электролитом. Например, в воздушно-цинковом элементе со щелочным электролитом (NaOH) протекает реакция Zn + ½ O₂ + 2NaOH = Na₂ZnO₂ + H₂O. Это реакция образования Na₂ZnO₂, к нему и относится .

Стандартное химическое сродство реакции между различными веществами подсчитывается по значениям по следующей формуле:

. (А)

Эта формула написана по аналогии с формулой для стандартного значения теплового эффекта [формула (8) в разделе «Закон Гесса»], так как величина G, как и Н, является функцией состояния, т.е. ее изменение не зависит от пути проведения реакции.

Пример. Константа равновесия реакции

Н₂ +I₂ = 2HI

= 50 при температуре 717 К . Определить нормальное химическое сродство при этой температуре и направление реакции.

Решение. По формуле (7)

кДж/кмоль.

Реакция протекает в сторону образования HI.

Зависимость химического сродства от температуры.

Как было выяснено в разделе «Сложные системы», уравнения Гиббса-Гельмгольца имеют вид:

и .

Будем рассматривать условия и перепишем первое уравнение иначе:

.

Поскольку , то

. (В)

Здесь  изобарный тепловой эффект и  изменение энтропии в реакции. Чтобы получить зависимость , нужно воспользоваться выражениями и . Зависимость теплового эффекта от температуры была получена раньше при условии. что теплоемкости реагирующих веществ выражаются многочленами:

Теперь получим выражение для изменения энтропии в зависимости от температуры. Для этого нужно проинтегрировать выражение

.

По уравнению Кирхгофа

,

откуда для реагирующей смеси .

Учитывая принятую зависимость теплоемкости от температуры, получим:

.

Проинтегрируем это выражение в пределах от стандартного состояния до состояния. соответствующего некоторой температуре Т и получим:

. (С)

Величина , входящая в , определяется по табличным данным. Выражение и полученное ранее выражение (см. раздел «закон Кирхгофа»)

подставим в (В). В результате будем иметь:

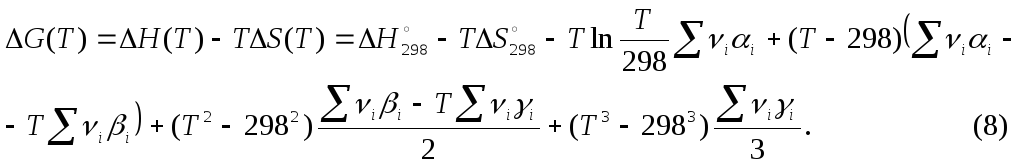
Зависимость константы равновесия от температуры.

Уравнения изобары и изохоры реакции. Уравнения изобары и изохоры реакции представляют собой дифференциальные уравнения, выражающие связь между константой равновесия, тепловым эффектом реакции и температурой.

Получим сначала уравнение изобары реакции. Для этого используем уравнение Гиббса-Гельмгольца и уравнение изотермы реакции:

;

.

Из закона действующих масс следует, что константа равновесия зависит от температуры. Продифференцировав второе уравнение по температуре, будем иметь:

.

Подставим этот результат в уравнение Гиббса-Гельмгольца и получим:

.

С учетом того, что , последнее уравнение приводится к виду:

. (8)

Полученное уравнение называется уравнением изобары реакции. По аналогии с ним можно написать уравнение изохоры реакции:

. (9)

В этих уравнениях H и U  тепловые эффекты реакций и соответственно. Напишем эти уравнения в обобщенном виде

, (10)

подразумевая под Q величины H или U, а под K  константы или .

Обобщенное уравнение называют уравнением изобары-изохоры реакции. Это уравнение позволяет исследовать характер смещения химического равновесия под влиянием изменения температуры. Фактором, который определяет направление смещения равновесия при изменении температуры, является знак теплового эффекта реакции. Действительно, если прямая реакция является экзотермической (Q < 0), то по уравнению (10) видно, что . Следовательно, при увеличении температуры () константа равновесия уменьшается , а это в свою очередь означает смещение равновесия реакции влево, т.е. переход к обратной реакции  эндотермической. Если же изначально происходит эндотермическая реакция (Q > 0) , то при увеличении температуры константа равновесия увеличивается: , т.е. равновесие смещается вправо  направление реакции не изменяется. Таким образом, повышение температуры всегда (при любом знаке теплового эффекта) смещает равновесие в направлении эндотермической реакции (т.е. в направлении, при котором происходит поглощение теплоты). Аналогично, понижение температуры всегда смещает равновесие в направлении экзотермической реакции (в направлении выделения теплоты).

Зависимость константы равновесия от температуры. Чтобы получить явную зависимость константы равновесия от температуры, проинтегрируем уравнение (10) и получим:

,

где J  произвольная постоянная интегрирования.

Подставим в этот интеграл зависимость теплового эффекта реакции от температуры:

,

причем для краткости обозначим , и . Тогда получим:

.

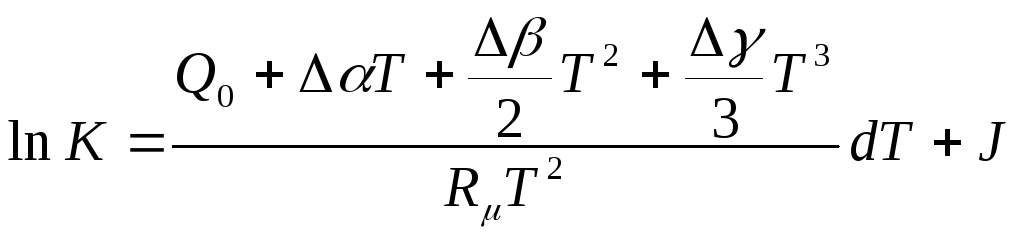Произведем интегрирование:

.

Перейдем к условиям :

. (12)

Чтобы по этому уравнению можно было подсчитывать значение константы равновесия при любой температуре (и при известных ), нужно сначала определить произвольную постоянную интегрирования J. Для этого требуются начальные условия, т.е. нужно иметь значение при какой-нибудь определенной температуре. Получить эти начальные условия можно из эксперимента, но экспериментальное определение очень сложно, и такой эксперимент может быть поставлен далеко не для всех веществ. Это обстоятельство является препятствием к тому, чтобы получить значение константы интегрирования J с помощью начальных условий.

В связи с этим возникла задача теоретического определения константы интегрирования J. Но необходимого условия для этого не дают ни 1-й, ни 2-й законы термодинамики. Поэтому понадобилось какое-то новое положение, не вытекающее из 1-го и 2-го законов термодинамики, с помощью которого можно было бы определить J. Такое положение было найдено в 1906 г. немецким физиком В. Нернстом. Он нашел опытную закономерность, которая получила название тепловой теоремы. В форме, первоначально установленной Нернстом, теорема применялась только к конденсированным системам, но затем ее использование было распространено и на газы.

Тепловая теорема Нернста. Из уравнения Гиббса-Гельмгольца

следует, что при Т = 0 химическое сродство и тепловой эффект становятся равными друг другу.

У Нернста имелся большой экспериментальный материал, накопленный им при изучении поведения веществ при низких температурах. Этот материал позволил Нернсту сделать вывод о том, что и не только равны друг другу при Т = 0, но еще что кривые и при приближении к абсолютному нулю имеют общую касательную, которая параллельна температурной оси, т.е. что .

При температурах, близких к абсолютному нулю, все вещества находятся в конденсированном состоянии, а для конденсированных систем и не зависят от давления. Поэтому отбросим индекс “р” и запишем:

.

Это выражение является формулировкой тепловой теоремы. Из нее следует, что при приближении к абсолютному нулю величины и перестают зависеть от температуры.

Определение константы интегрирования J для конденсированных систем. Продифференцируем по температуре уравнение изобарного теплового эффекта

и получим:

.

В соответствии с теоремой Нернста

,

откуда следует. что для конденсированных систем при величина . Подставим этот результат в уравнение (12):

.

Умножим обе части уравнения на и учитывая, что , получим:

.

Это выражение продифференцируем по Т:

.

Произведение двух констант есть новая константа. Применим к последнему выражению теорему Нернста:

.

Отсюда следует, что , т.е. константа интегрирования для конденсированных систем равна нулю.

На основе этого результата получена формула для вычисления константы интегрирования газовых реакций . Эту формулу запишем без вывода:

.

Величины называются химическими константами. Они рассчитываются по экспериментальным значениям калорических величин (теплоемкостей и теплот парообразования веществ) и сводятся в таблицы. С учетом этих табличных данных константы равновесия газовых реакций рассчитываются по формуле Нернста:

.

(С выводом формулы Нернста можно познакомиться по книге С.И. Исаева “Термодинамика”, 2000 г., § 19.5).

Третий закон термодинамики. Значение тепловой теоремы Нернста оказалось шире, чем только условие для определения константы интегрирования уравнения для константы равновесия. Оказалось, что эта теорема может быть представлена в форме утверждения, рассматриваемого как новый закон.

Выражение можно представить в другом виде. Поскольку , то

, (13)

т.е. при химическая реакция протекает так, что энтропия системы не изменяется. Это означает, что при приближении к абсолютному нулю температуры энтропия всех участвующих в реакции веществ стремится к некоторой предельной величине . Исходя из квантовой теории, М. Планк показал, что, хотя это предельное значение само по себе не играет роли, оно может быть принято равным нулю:

. (14)

Это положение не является следствием ни 1-го, ни 2-го законов, поэтому оно было наименовано 3-м законом термодинамики.

В связи с выражением (14) Э. Ферми дает следующую формулировку: «Энтропия любой системы при абсолютном нуле температуры всегда может быть принята равной нулю». На основании этого, пишет Ферми, энтропию некоторого состояния А определяем интегралом

,

где интеграл берется вдоль обратимого процесса, начинающегося состоянием системы при и заканчивающегося состоянием А.

Таким образом, третий закон термодинамики определяет начало отсчета энтропии. Значение энтропии, отсчитанное от нуля, называется абсолютной энтропией². Значения абсолютной энтропии определяются по калорическим данным  теплоемкостям и тепловым эффектам фазовых переходов (см. в книге С.И. Исаева “Термодинамика”, 2000 г., § 19.4). Они подсчитаны для многих веществ и сведены в таблицы.

Из 3-го закона термодинамики вытекает важное следствие о поведении теплоемкостей и вблизи абсолютного нуля температуры. В разделе «Дифференциальное уравнение состояния» были получены калорические уравнения состояния:

и ,

откуда следует

и .

Проинтегрируем, например, второе уравнение:

. (15)

Допустим, что при теплоемкость не равна нулю. Тогда разложение в степенной ряд обязательно должно содержать слагаемое в нулевой степени:

.

Подставим этот многочлен в интеграл (15) и получим:

.

Возьмем предел

,

что противоречит 3-му закону термодинамики, по которому . Следовательно, принятое допущение было неверным. Поэтому

и .

Некоторые формулировки 3-го закона термодинамики. Поскольку при приближении к абсолютному нулю температуры энтропия не изменяется, то процессы в этой области протекают без теплообмена. Следовательно, нельзя понизить температуру тела до путем отвода от него теплоты. В связи с этим 3-й закон термодинамики формулируется в виде принципа недостижимости абсолютного нуля: «Абсолютный ноль температуры недостижим». М. Планк так сформулировал третий закон термодинамики [см. выражение (14)]: «Энтропия всех тел безгранично уменьшаетcя при безграничном уменьшении температуры». Этим и утверждается положение о недостижимости абсолютного нуля: хотя значение энтропии при Т = 0 есть нуль, но достигнуть этого состояния охлаждением тела невозможно; можно только сколь угодно близко приблизиться к нему.

Еще одна формулировка: «Невозможно создать вечный двигатель третьего рода». Иначе говоря, невозможно создать машину, которая в качестве низшего источника теплоты (теплоприемника) имела бы тело с температурой 0 К. При этом термический к.п.д. цикла Карно был бы равен единице, но это невозможно в связи с недостижимостью абсолютного нуля температуры.

1 В этом смысле говорят о химической обратимости реакции.

2 Надо быть осторожным в понимании физического содержания уравнения (14); по смыслу его введения оно представляет собой только математический эквивалент уравнения (13). Поэтому термин абсолютная энтропия имеет достаточно условный характер.