Устройства СВЧ и антенны (90

Приложение 1.

ИЗЛУЧЕНИЕ ВИБРАТОРОВ КОНЕЧНОЙ ДЛИНЫ

П1.1. Электрический вибратор

Рассмотрим излучение так называемого симметричного электрического вибратора, который является простейшей антенной и вместе с тем составным элементом многих сложных антенных систем.

Рис.6. Симметричный вибратор.

Симметричный вибратор представляет собой прямолинейный цилиндрический проводник длиной 2l и радиусом a, питаемый в центре генератором высокой частоты (рисунок 6). Присоединение генератора высокой частоты к вибратору может быть произведено, например, посредством двухпроводного фидера.

Под воздействием э. д. с. генератора в вибраторе возникают электрические токи, которые распределяются вдоль вибратора таким образом, что создаваемое в окружающем пространстве электромагнитное поле удовлетворяет, во-первых, уравнениям Максвелла и, во-вторых, граничным условиям. Если, как мы и будем предполагать в дальнейшем, вибратор является идеально проводящим (проводимость ), то граничные условия на поверхности вибратора сводятся к тому, что тангенциальная составляющая напряженности электрического поля всюду, за исключением точек приложения сторонней э. д. с., равна нулю. В точках приложения сторонней э. д. с., т. е. на участках действия генератора высокой частоты, нулю равна сумма тангенциальных составляющих сторонней э. д. с. и напряженности электрического поля.

Задача об излучении электромагнитных волн сводится прежде всего к установлению связи между током в вибраторе и электромагнитным полем, которое создается этим током. Если распределение тока в вибраторе задано, то электромагнитное поле легко определяется соответствующими уравнениями. Однако распределение тока вдоль вибратора заранее неизвестно, и поэтому задача об определении поля в пространстве значительно усложняется.

В строгой электродинамической постановке существуют два метода решения задачи о возбуждении вибратора, а именно метод интегрального уравнения и метод собственных функций. Перейдем к краткому рассмотрению первого метода.

П1.2. Метод интегрального уравнения

Пусть имеется в свободном пространстве бесконечно тонкая магнитная рамка в виде кольца радиуса a и ширины b . Векторный потенциал этой рамки определяется формулой

где интегрирование производится по поверхности рамки и плотности поверхностного магнитного тока.

В рассматриваемой здесь задаче магнитный ток в цилиндрической системе

дующему выражению азимутальной составляющей векторного потенциала магнитной рамки:

Внесем в поле магнитной рамки симметричным образом круглый идеально проводящий электрический проводник радиуса а и длины 2l. Под влиянием поля магнитной рамки на проводнике возникнут поверхностные электрические токи, которые на боковой поверхности проводника имеют продольные составляющие Jzý , а на торцевых поверхностях проводника радиальные состав-

ляющие Jrý .

Для того чтобы упростить выкладки и не связывать себя с наличием электрических токов на торцовых поверхностях, можно представить проводник в виде круглой трубы с бесконечно тонкими стенками (рисунок. 7). Тогда наводимые токи имеют только продольные составляющие и текут как по внешней, так и по внутренней поверхности трубы.

Рис.7. К методу интегрального уравнения: 1 - магнитная рамка; 2 - проводящая трубка.

R1 (z z )2 a2 ,

— постоянная величина, малая по сравнению с длиной волны. Но так как для

стремится к бесконечности и выражение (1.8) становится все более точным, поскольку отбрасываемая часть интеграла в (1.4) имеет при этом конечную величину.

Будем предполагать далее, что сторонняя э. д. с. приложена на участке бесконечно малой длины провода в центре вибратора. Поскольку радиус провода а мал по сравнению с длиной волны, можно действие магнитной рамки заменить действием эквивалентного ей электрического диполя, положив момент диполя равным Izýl i J M b a2 . Векторный потенциал этого диполя во всех точках про-

вода, за исключением точек, в которых действует сторонняя э. д. с, имеет конечную величину, малую по сравнению с величиной, определяемой формулой

(1.8).

Таким образом, для всех точек вибратора, за исключением тех точек, в которых приложена сторонняя э. д. с, и тех точек, в которых ток может быть равен

Это есть так называемое телеграфное уравнение, которое имеет место в длинной линии без потерь. Имея в виду, что ток на концах вибратора равен нулю, и обозначая ток в точках питания вибратора через I 0 , решение уравнения (1.10) получим в виде:

В том же приближении можно получить и распределение электрического заряда в вибраторе. Используя уравнение непрерывности, которое для линейного тока запишется в виде:

Таким образом, в тонком вибраторе ток и заряд приближенно распределяются по закону синуса. Однако, как следует из самого вывода выражения (1.11), распределение тока в вибраторе при стремлении радиуса провода к нулю только стремится к синусоидальному распределению, никогда не становясь синусоидальным. В частности, выражение (1.11) несправедливо для узлов тока, где ток не подчиняется закону синуса и не равен нулю.

В теории антенн в большинстве случаев полагают ток в симметричном вибраторе распределенным по закону, определяемому формулой (1.11). Это позволяет в значительной степени упростить все расчеты и в большинстве случаев получить результаты, близкие к действительным.

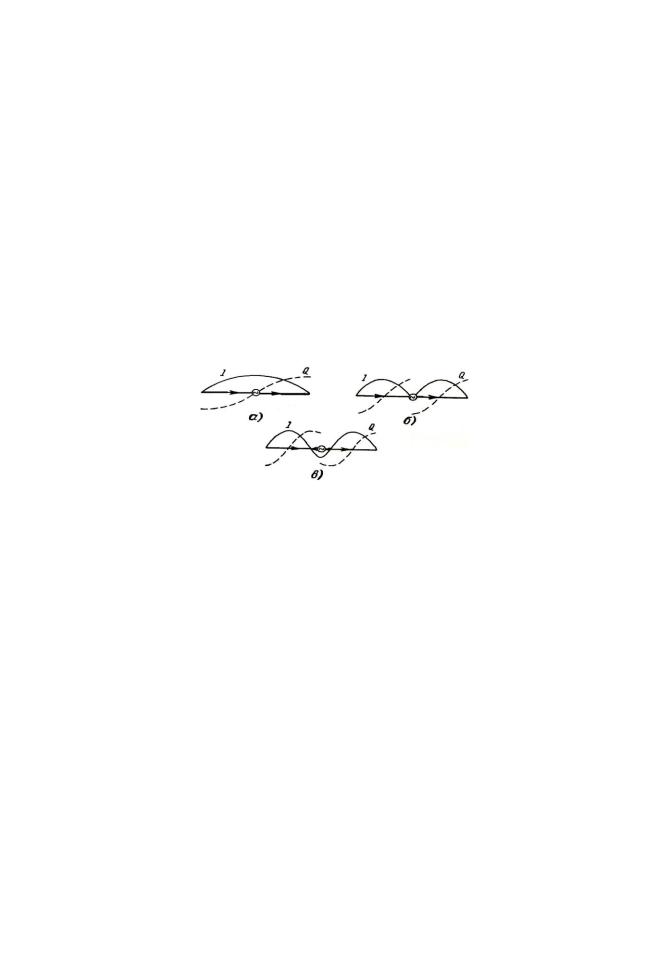
Из формул (1.11) и (1.12) следует, что:

а) на концах вибратора устанавливаются узлы (нули) тока и пучности заряда; б) на расстоянии четверти длины волны от концов вибратора образуются пуч-

ности тока и узлы (нули) заряда. Затем еще через четверть длины волны образуются опять узлы тока и пучности заряда и т. д.;

в) ток и заряд в каждой точке вибратора сдвинуты между собой по фазе (во времени) на угол 90°;

Рис.8. Распределение тока и заряда в симметричном вибраторе

г) в точках питания вибратора устанавливается пучность, узел или промежуточное значение тока в зависимости от отношения длины вибратора к длине волны;

д) фаза тока и заряда меняются вдоль вибратора скачками на 180° при переходе через нуль.

На рисунке 8 приведено несколько характерных случаев распределения тока и заряда вдоль вибратора. Заметим, что симметричный вибратор, общая длина 2l которого равна половине длины волны, называется полуволновым вибратором. Вибратор, длина 2l которого равна длине волны, называется волновым вибратором.

В дальнейшем всюду, за исключением особых случаев, мы будем предполагать распределение тока по закону синуса.

П1.4. Напряженность поля вибратора в зоне излучения

Пусть распределение тока в вибраторе будет задано. Тогда можно определить поле вибратора в любой точке пространства, в том числе и в бесконечно удаленных точках, т. е. в зоне излучения. При этом вследствие того, что вибратор тонкий, пренебрежем излучением магнитного тока, образованного разрывом в центре вибратора.

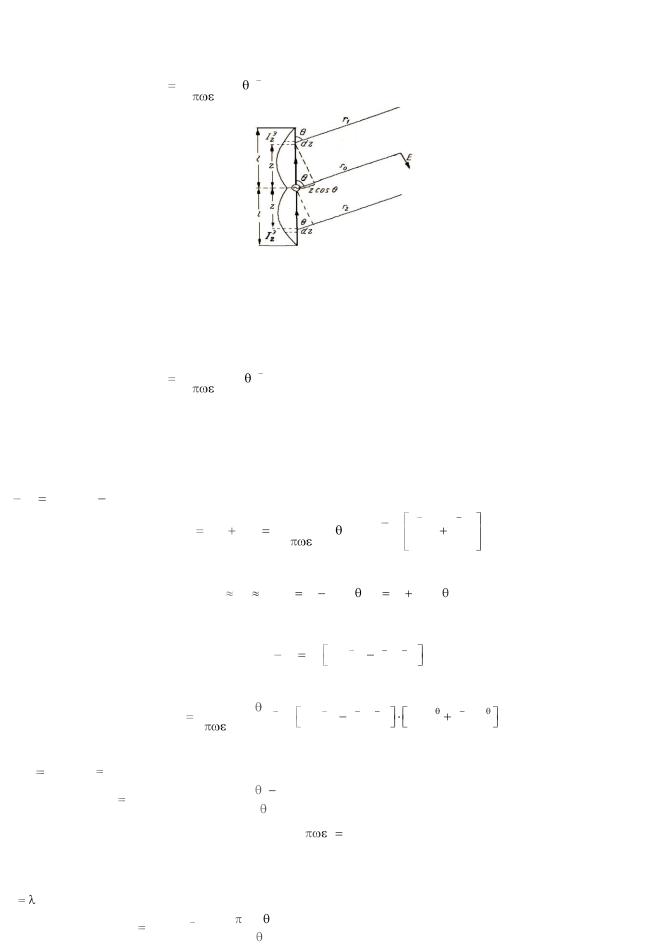
Обращаясь к рисунку 8, выделим в точке z провода элемент длины dz . Напряженность электрического поля, создаваемого элементом dz вибратора в зоне излучения равна:

Рис.8. К вычислению напряженности поля симметричного вибратора.

Напряженность поля, создаваемого элементом dz, симметрично расположенным относительно центра вибратора, в той же точке пространства равна:

блюдения бесконечно удалена, а практически находится на расстоянии, значительно превышающем длину вибратора.

Производя интегрирование этого выражения по длине вибратора в пределах

Формула (1.15) определяет напряженность электрического поля симметричного вибратора в зоне излучения. В частности, для полуволнового вибратора ( l / 4 ) эта формула принимает вид:

Кривые, описываемые формулой (1.15) и дающие зависимость величины напряженности поля Е от угла наблюдения , называются диаграммами (характеристиками) направленности вибратора в его меридиональной плоскости. Диаграммы направленности строятся обычно в полярных координатах (иногда они строятся в декартовых координатах).

Заметим, что в экваториальной плоскости вибратора вследствие осевой симметрии излучение является равномерным и поэтому диаграмма направленности вибратора в этой плоскости в полярных координатах представляет собой круг.

Отметим еще, что фаза напряженности поля от угла наблюдения не зависит и с точки зрения наблюдателя, находящегося в зоне излучения, кажется, что волны исходят из точки, совпадающей с центром вибратора. Эта точка обычно

Рис. 9. Диаграммы направленности симметричного вибратора: а) – l / 4 ; угол раствора 800 ; б) – l / 2 ; угол раствора 440 ;

в) – l 5 / 8 ; угол раствора 310 .

На том же рисунке приведены значения углов раствора диаграмм направленности, т. е. углов, в пределах которых напряженность поля не падает ниже, чем в 2 раз, по сравнению с напряженностью поля в направлении максимального излучения. Этот угол раствора часто называют шириной диаграммы направленности по половинной мощности.

Анализ формулы (1.15) и кривых рисунке 9 показывает, что с укорочением

длины волны (при неизменной длине вибратора) в пределах от l / 4 до l / 2

увеличиваться. Так, например, при l в направлении = 90° излучение отсутствует.

Заметим, что в направлении оси вибратора, так же как и в направлении оси диполя, излучение всегда равно нулю.