Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет параметров настройки цифровых регуляторов (90

..pdf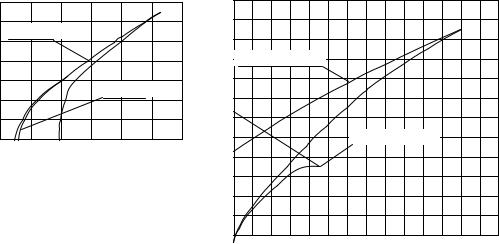

Скачиваний:

Добавлен:

15.11.2022

Размер:

502.77 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

На объекте установлена одноконтурная АСР с дискретным ПДД(2)- алгоритмом регулирования.

Корреляционная функция приведенного к выходу системы регулирования возмущающего воздействия:

где γ =1/ T0, a T0 =78 ч.

R x (τ)= Dx (1+ γ

)e−γ

(8. 5)

Z - преобразование КЧХ объекта управления и демодулятора имеет вид:

−1

−αcT

−βcT

−r

WμWдм(z) = Kμ(1−z

)

α−β z −e

−αT

−

α−β z −e

−βT

(8. 6)

z −1

где α =1/ T1, β =1/ T2, r - целая часть от деления τ на Т, а c =1 − (2/ T − r). Используя формулы (6. 27) и (6. 28) расчета настроек ПДД(2)-алгоритма регулирования и варьируя параметром Кдд для достижения максимального значения Кп определим области заданного запаса устойчивости для m=0,54 при шагах дискретизации Т=4 ч; T=8 ч; T=24 ч; Т=96 ч. Графики областей заданного запаса устойчивости приведены на рис. 20.

Кд350
300	Т=4 Кдд=685
250
200
150				Т=8 Кдд=634
100				Т=8 Кдд=634
100
50
00		10	20	30	40	50 Кп60

Кд50
40
30	Т=24 Кдд=615
20
10
0
-10				Т=96 Кдд=997
-20				Т=96 Кдд=997
-20
-30
-40
-50
-60
-700		1	2	3	4	5	6 Кп7

Рис. 20. Графики линий заданного запаса устойчивости (m=0,54) односвязной одноконтурной ДНСУ с ПДД(2)-алгоритмом регулирования при различных шагах дискретности Т

Выбирая для каждого Т максимальное Кп, определим относительную дисперсию

ошибки регулирования в моменты прерывания (Dy/Dx) и осредненную на интер-

вале Т относительную дисперсию (Dy / Dx ) . Для определения дисперсии найдем

Z-преобразование корреляционной функции Rx(τ) (см. приложение 5, 6).

−1

T z e

−βT

T z

−1

−βT

Sx (z) = DxT

+β

−1 ,

−βT

−1

−e

−βT

(z −e

−βT

−1

−e

−βT

z −e

)

(8.7)

Подставляя (6. 26), (8. 6) и (8. 7) в (7. 4) и (7. 7), рассчитаем соответствующие дисперсии регулируемой величины.

Таблица 2 Значение настроек дискретного ПДД(2)-алгоритма регулирования

и значения дисперсий регулируемой величины (в моменты прерывания и среднеинтервальная)

Т	Кдд	Кп	Кд	Dy/Dx		Dy	/Dx
4	685	53,5	328,0	0,0037	0,0040

8	634	22,5	167,0	0,0141	0,0199

24	615	6,01	39,5	0,1031	0,1683

96	997	2,22	-30,0	0,5735	0,8274

Как следует из табл. 2, эффективность системы регулирования при увеличении шага дискретизации с 4 до 96 часов уменьшается примерно в 200 раз. Различие в среднеинтервальной дисперсии и дисперсии в точках прерывания увеличивается при этом с 8,1 до 44,3 %.

В приложении приведены примеры некоторых непрерывных функций f(t), часто встречающихся в задачах управления, их преобразования по Лапласу, Z- преобразования соответствующих решетчатых функций, а также модифициро-

ванные Z-преобразования F*(c,z)(0 ≤ c <1) [6, 5].

ПРИЛОЖЕНИЕ

Преобразование Лапласа, Z-преобразование, расширенное Z-преобразование

Таблица П

№

f(t)

F(p)

F*(z)

F*(c,z)

п/п

δ(t)

z-1

1(t)

z −1

T[c z +(1−c)]

, где с =1−

(z −1)2

T2z(z +1)

c2z2 + z(1+ 2c − 2c2 )+ (1−c)2

(z −1)3

e-αt

e−αcT

p + α

z −e−αT

z − e−αT

te-αt

Tze−αT

Te−αcT [c z +e−αT (1−c)]

(p + α)2

(z −e−αT )

−αT

−2αT

(z +e−αT )

−αcT e−2αT (z +e−αT )

ce−αT

(p + α)

−αT

(z −e

)

2(z −e

2(z −e−αT )

(z −e−αT )

)

Продолжение табл. П

e-αt- e-βt

β − α

e−αcT

e−βcT

(z −e−αT )−

(z −e−βT )

(z −e−αT )−

(z −e−βT )

(p + α)(p +β)

e−αT

e−αcT

(β − α)(γ − α)(z − e−αT )−

(β − α)(γ − α)

e−βT

−

e−βcT

(α −β)(γ −β)(z − e−βT )

−

(α −β)(γ −β)(z − e−βT )−

(α −β)(γ −β)

e−γ t

−

e−γcT

(p + α)(p +β)(p + γ)

(α − γ)(β − γ)(z − e−γT )

−

(α − γ)(β − γ)

(α − γ)(β − γ)(z − e−γT )

−βt

−αT

α −β

)

−

− e

(α −β)

−

cT(

(z − e

−βT

)

−αT

)

+ (α −β)t e−αt

− e

e−βcT

z − e−αT

(p +β)(p + α)2

−αcT

−αT

(α −β)Te−αT

(α −β)Te

(z − e

−βT

)

(

(z − e−αT )2

− e−αT 2

1 − e−αT

(1 − e−αT )z

e−αcT

p(p + α)

(z −1)(z − e−αT )

− (z − e−αT )

z −1

1 − (1 − αt)e

−αT

−

αTe

−αT

+ αcT

αTe−αT

−αcT

− e−αT )

(z − e

p(p + α)2

z −1

−αT

−

(z − e

−αT

)

(z − e−αT )

1 2

131 − e−αT ×

×1 − αt − α2t2

14βe−αt

1+ α −β −

−αe−βt

α −β

15α2e−βt

1− (α −β)2 +

−ααβ−β t e−αt +

+[2αβ−β2 ]e−αt (α −β)2

α3

p(p + α)3

αβ

p(p + α)(p +β)

α2β

p(p + α)2 (p +β)

Продолжение табл. П

αTe−αTz

e−αcT

αTe−αcT [cz + e−αT (1 − c)]

−

(z −e−αT )−

−

(z − e−αT )

−

(z − e−αT )2

−

z −1

(z − e−αT )2

z −1

−αT

−2αT

−

α2T2e−αcT

−α2

−αT

2(z − e−αT )

(z −e−αT )

(2c

+1)e

−αT

z − e

(z − e−αT )

β z

β e−αcT

(α −β)(z − e−αT )−

z −1

−

α z

α e−βcT

(α −β)(z − e−βT )

−

(α −β)(z − e−βT )

α2 z

α2 e−βcT

(

)

z −1 − (α − β) (z − e−αT )+

z −1 − (α−β)2 z −e−βT

[αβ + β(α − β)]z

β(α−β)+(1+αcT)+αβ

αβTe−αT

(z − e

−αT

)

(α−β)2 (z −e−αT )

(α − β)

(α−β)(z −e−αT )

αβTe−αTz

×e−αcT

(α − β)

(z − e−αT )2

Продолжение табл. П

βγe−α t

αβγ

β γz

β γ e−αcT

1−

−

(β − α)(γ − α)(z − e−αT )−

−

(β − α)(γ − α)(z − e−αT )−

p(p + α)(p +β)(p + γ)

z −1

(β−α)(γ −α)

z −1

αγe−β t

−

γ α z

−

γ α e

−βcT

−

(γ −β)(α −β)(z − e

−βT

)

(γ −β)(α −β)

(γ −β)(α −β)(z − e−βT )

−γ t

−

αβe

−

α β z

α β e−γc T

(α − γ)(β − γ)(z − e−γT )

(α − γ)(β− γ)

−

(α − γ)(β − γ)(z − e−γT )

cos ω0t

z2 − zcosω0T

zcoscω0T − cos(1 − c)ω0T

p2 + ω02

z2 − 2zcosω0T +1

sin ω0t

ω0

zsin ω0T

zsin cω0T + sin(1 − c)ω0T

p2 + ω2

z2 − 2zcosω

T +1

z2 − 2zcosω

T +1

e−αT cos ω0t

p + α

z(z − e−αT cosω0T)

e−αcT [zcoscω0T − e−αT cos(1 − c)ω0T]

(p + α)2 + ω02

z2 − 2ze−αT cosω0T + e−2αT

−αT

sin ω0t

ω0

−αT

sin ω0T

−αcT

[zsin cω0T + e

−αT

sin

(1 − c)ω0T]

(p + α)2 + ω02

z2 − 2ze−αT cosω0T + e−2αT

Продолжение табл. П

α2 + ω2

1 − e−αT secΘ×

−

z −1

×cos(ω t

− Θ),

z −1

гдеΘ =0

p[(p + α)2 + ω02

]

−

z 2

− z e−αT

secΘcos(ω0T −Θ)

−

secΘ[z cos(cω0T + Θ)−e−αT cos((1−c)ω0T −Θ)]

z 2 − 2z e−αT cosω0T + e−2αT

−

2z e

−αT

cosω0T + e

−2αT

= arctg −

ω0

Примечания:

1.При необходимости вычисления Z-преобразования для более сложных объектов регулирования необходимо провести разложение формулы F(p) на сумму простых дробей. Далее применяется Z-преобразование с использованием настоящего приложения для каждого члена суммы.

2.При наличии в числителе КЧХ объекта регулирования оператора (р + δ) дробь F(p) разбивается на сумму двух дробей. Далее применяется Z-преобразование с использованием настоящего приложения для каждой дроби.

Формулы модифицированного Z-преобразования приведены для значения τ, меньшего Т. Для значений τ≥Т необхо-

димо воспользоваться модифицированным Z-преобразованием со значением с = 1-( τ/ Т- r), где r – целая часть от деле-

ния τ на T и полученный результат умножить на z-r.

СПИСОК ЛИТЕРАТУРЫ

1.Волгин, В. В. К вопросу выбора запаса устойчивости в системах автоматического регулирования тепловых процессов / В. В. Волгин, В. Я. Яки-

мов // Теплоэнергетика, 1972. – №4. – С. 76 – 78.

2. Методы расчета систем		автоматического регулирования: учеб. посо-
бие /	Н. П. Бувин [и др.];	под общ. ред. В. В. Волгина. – М.: МЭИ,
1972.	– 192с.

3.Ротач, В. Я. Расчет систем автоматического регулирования с цифровыми регуляторами: учеб. пособие. / В. Я Ротач. – М.: МЭИ, 1992. – 64 с.

4.Волгин, В. В. Сравнительный анализ эффективности цифровых алгорит-

мов стабилизации качества электрохимического стекла, производимого в ванных печах непрерывного действия / В. В. Волгин, В. А. Ажикин, А. А. Земсков, А. В. Мухин // Теория и практика построения и функционирования АСУ ТП : сб. научн. тр. – М.: МЭИ, 1993. – С. 80 – 89.

5.Ротач, В. Я. Теория автоматического управления теплоэнергетическими процессами / В. Я. Ротач. – М.: Энергоатомиздат, 1985. – 296 с.

6. Джури, Э. Импульсные системы автоматического регулирования / Э. Джури. – М.: Физматгиз, 1963. – 456 с.

7.Волгин, В. В. Расчет настроек дискретно-непрерывных систем управления / В. В. Волгин, В. А. Ажикин; под общ. ред. В. С. Мухина. – М.:

МЭИ, 2000. – 20 с.

	ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ..............................................................................................................		3
1.	Динамические системы и их характеристики..................................................	4
2.	Развёрнутая схема цифрового канала регулирования...................................	14
3.	Аналоговый вариант расчета цифровых регуляторов...................................	16
4.	Дискретный вариант расчета цифровых регуляторов...................................	17
5.	Методика расчёта коэффициента передачи объекта К* ...............................	18
6.	Расчет настроек цифровых алгоритмов управления на заданный запас
устойчивости..........................................................................................................		29
7.	Оптимизация настроек цифровых алгоритмов регулирования....................	35
8.	Примеры расчета...............................................................................................	38
ПРИЛОЖЕНИЕ.....................................................................................................		42
СПИСОК ЛИТЕРАТУРЫ.....................................................................................		47
	Учебное издание
	Грименицкий П. Н.
	Лабутин А. Н.
	Головушкин Б. А.
	Расчет параметров настройки цифровых регуляторов

Учебное пособие для студентов специальности «Автоматизация технологических процессов и производств»

Редактор О. А. Соловьева Подписано в печать 5.12.2008. Формат 60 × 84 116 . Бумага писчая.

Усл. печ. л. 2,79. Уч.-изд. л. 3,10. Тираж 100 экз. Заказ

ГОУ ВПО Ивановский государственный химико-технологический университет

Отпечатано на полиграфическом оборудовании кафедры экономики и финансов ГОУВПО "ИГХТУ"

153000, г. Иваново, пр. Ф. Энгельса, 14.

<<< < Предыдущая 1 2 3 45 / 55

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022174.28 Кб6Расчет напряженности магнитного поля плоского витка с током (80..pdf
#
15.11.2022597.24 Кб7Расчет нелинейных магнитных цепей (96..pdf
#
15.11.20221.15 Mб7Расчет нелинейных электрических цепей (96..pdf
#
15.11.20221.1 Mб2Расчет параметров и характеристик гладкого цилиндрического соединения (90..pdf
#
15.11.2022502.37 Кб103Расчет параметров намотки композитных оболочек цилиндрических баллонов и корпусов двигателей (96..pdf
#
15.11.2022502.77 Кб6Расчет параметров настройки цифровых регуляторов (90..pdf
#
15.11.2022524.41 Кб5Расчет параметров распределенной информационно-управляющей системы (90..pdf
#
15.11.2022965.3 Кб34Расчет переходных состояний методами квантовой химии Учебно-методическое пособие..pdf
#
15.11.2022189.85 Кб4Расчет плоской стержневой системы на компьютере (90..pdf
#
15.11.2022229.88 Кб25Расчет поступлений вредных веществ в воздух рабочей зоны (96..pdf
#
15.11.20221.19 Mб4Расчет потерь тепла и инфильтрации для помещений (90..pdf