Согласованный фильтр для м-сигналов

Формирование М-сигналов. В последнее время в радиолока­ции и связи все более широко применяют сложные широкополосные сигналы. Одним из способов получения таких сигналов является изменение фазы высокочастотных колебаний по закону М-после­довательностей, строящихся, в свою очередь, на основе линейных рекуррентных последовательностей.

Линейной рекуррентной последовательностью называется периодическая последовательность символов удовлетворяющая рекуррентному правилу

(25)

где символы последовательности и коэффициенты прини­мают значения из области, а сложение и умножение производится по модулюр . Предполагается, что р есть простое число. Здесь число n - память последова­тельности, число р - основание последовательности, а наимень­шее число L, при котором - период или длина последовательности. Коэффициентв дальнейшем будем считать равным нулю.

Соотношение (25) называется правилом кодирования. В случае двоичной последовательности значения символов последо­вательности и коэффициентов равны либо единице, либо нулю, а суммирование ведется по mod2, которое определяется так

.

Из определения линейной рекуррентной последовательности вытекает, что для ее построения необходимо знать первые n чле­нов последовательности и правило кодирования, т.е. уравнение (25).

Пример. Пусть p=2 , n = 4, начальное слово - 1111, правило кодирования Тогдаи т.д. Построенная последовательность имеет вид 111100010011010.

По уравнению (25) нетрудно представить и схемную реали­зацию устройства, генерирующего последовательность. Оно должно содержать блок памяти, предназначенный для запоминания n последних выбранных членов последовательности, и комбинацион­ную схему, работа которой определяется заданным правилом кодирования.

На рисунке 2 представлена функциональная схема генератора линейной рекуррентной последовательности. Генератор состоит из n триггеров, выполняющих роль элемен­тов памяти, и устройства обратной связи, описываемого некото­рой булевой функцией¹

где - состояниеi-й ячейки памяти (i-го триггера), принимающее значение 0 или 1. Триггеры соединены между собой таким образом, что образуют регистр сдвига. Генератор работает oт внешних запускающих импульсов, называемых тактовыми.

Рассмотрим процесс генерирования последовательности символов. Пусть в исходном положении состояния ячеек регистра сдвига совпадают соответственно с символамиС приходом тактового импульса записанная в регистре информация сдвигается в сторону старше­го

разряда. Символ выходит из регистра, а в освободив­шуюся первую ячейку записывается символ с выхода устройства обратной связи. Теперь состояния ячеек регистра сдвигабудут определяться какгде

. С приходом следующего тактового импульса на выходе регистра появляется символ , а в первую ячейку записывается символ

. При этом состояния ячеек памяти будут совпадать соответственно с символамиПоявляющаяся на выходе регистра последовательность является линейной рекуррентной.

Период генерируемой последовательности зависит от выбран­ного правила кодирования и начального состояния регистра . В частности, если все ячейки регистра сдви­га находятся в нулевом состоянии, то независимо от правила ко­дирования на его выходе получается последовательность, состоя­щая из одних нулей. Поэтому максимальный период линейной рекур­рентной последовательности равен, гдеn - память последовательности. Последовательности с периодом называются линейными рекуррентными последовательностями максимального периода, или М-последовательностями. Для их получе­ния необходимо выбрать правило кодированиятаким образом, чтобы многочленбыл примитивным².

Можно показать, что для любого n число примитивных многочленов

определяется как , где- функция Эйлера в теории чисел, равная количеству целых поло­жительных чисел, меньшихL и взаимно простых с L , включая единицу.

В качестве примера приведем все примитивные многочлены для n=5:

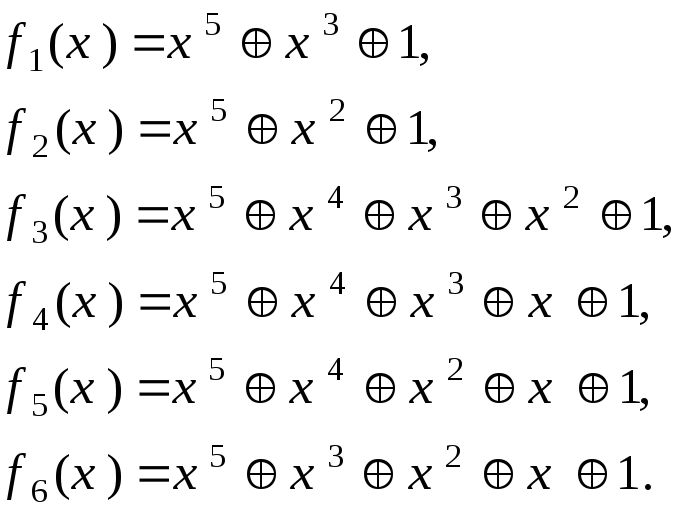
Любой из них может быть использован для получения М-последователъности. Так, для многочлена правило кодирования

Заметим, что чем больше членов содержится в многочлене , тем сложнее генератор.

Учитывая, что М-последовательности нашли ши­рокое применение в технике связи, укажем их основные свойства.

1. М-последовательность с периодом содержит все возможные комбинацииn-значных двоичных чисел за исключением нулевой.

2. Число единиц в М-последовательности на единицу больше числа нулей, причем появление единицы и нуля для постороннего наблюдателя, не знающего закон формирования последовательности, случайно во времени.

3. Результат почленного суммирования М-последовательности с этой же последовательностью, но сдвинутой на i символов, где 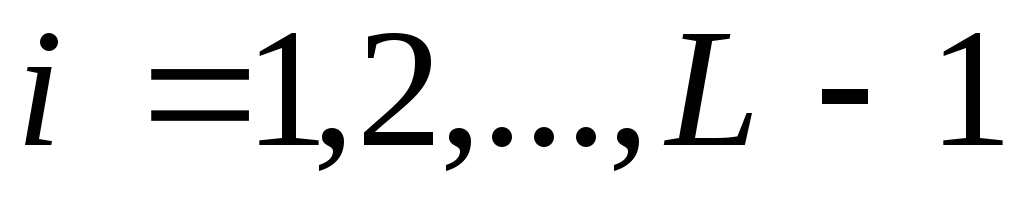, представляет собой исходную последовательность, но сдвинутую на некоторое другое число символов.