СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………………………………2-3

1. Понятие энтропии.

1. Статистический смысл понятия энтропии…………………………4-5

2. Энтропия как мера степени неопределенности……………………5-6

2. Понятие об информации.

   1. Формы информации……………………………………………………7

   2. Негативное влияние информации……………………………………..8

   3. Измерение информации.

      1. Мера Р. Хартли………………………………………………….8-9

      2. Мера К. Шеннона……………………………………………...9-10

      3. Термодинамическая мера……………………………………10-11

      4. Энергоинформационная (квантово-механическая) мера……..11

3. Теорема Шеннона о кодировании при наличии помех……………...11-12

4. Пример использования энтропии в прогнозировании.

   1. Ее  значение для прогнозирования………………………………..12-14

   2. Применение к рискам…………………………………………...…14-15

ЗАКЛЮЧЕНИЕ……………………………………………………………….16

БИБЛИОГРАФИЯ…………………………………………………………….17

ВВЕДЕНИЕ

Предмет работы: энтропия и информация.

Цель работы: изучение энтропии и информации, а так же: какое применение имеют данные понятия к рискам.

В ходе данной работы предстоит решить несколько задач: рассмотрение понятия энтропии и информации, статистического и термодинамического смысла энтропии, так же определение данного понятия, как меры степени неопределенности, теоремы Шеннона о кодировании при наличии помех, использования энтропии в прогнозировании и применения энтропии к рискам.

Данная тема является злободневной, так как широко пользуются в физике, химии, биологии и теории информации. Клаузиузус первым же в 1865 году положил начало применению понятия энтропия на основе анализа тепловых машин. Трудно найти определения более общие для всех наук (не только естественных), чем энтропия и информация. Возможно, это связано с самими названиями. С тех пор энтропия многократно фигурировала в знаменитых спорах. Например, в исторической науке энтропия имеет не малое значение для объяснения экспликации феномена вариативности истории.

Существующему давно понятию “информация” , был придан математически точный смысл К.Шенноном. Это как приводило, так и приводит ко многим недоразумениям, поэтому очень важно уделить данному понятию должное внимание. Никакая информация, никакое знание не появляется сразу - этому предшествует этап накопления, осмысления, систематизации опытных данных, взглядов. Информация является общим компонентом для всех наук, она связывает между собой различные по характеру и содержанию науки, поэтому информационные процессы, которые изучаются информатикой, имеют место во многих предметных областях.

Нельзя ограничивать информационные процессы рамками вычислений и пассивного получения или преобразования информации. Эти процессы сложны и многообразны. Важно научить новое поколение это понимать. Информация не всегда связана с компьютером. Чаще всего именно человек активно ее обрабатывает. Умение в процессе обработки не только анализировать, но и синтезировать из отдельных крупинок информации целое - весьма ценное качество человека будущего.

Я согласна с необходимостью изучения понятия энтропии, синергетики, социальной информатики, эволюции и т.п.

1. Понятие энтропии.

   1. Статистический смысл понятия энтропии.

Вероятностное толкование понятия энтропии было дано в статистической физике Людвигом Больцманом. Введем для начала понятие термодинамической вероятности (W). Термодинамическая вероятность означает число возможных неотличимых микроскопических состояний системы реализующих определенное макроскопическое состояние этой системы.

Б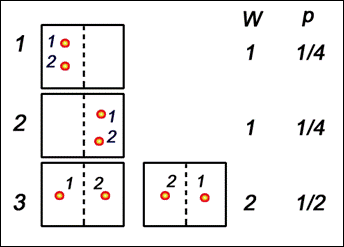удем рассматривать простую систему всего из двух неотличимых молекул, которые находятся в некотором объеме. Мысленно разделим этот объем на две части, и, пронумеровав молекулы, найдем число способов, которым можно разместить их в этих двух частях.

М

Рисунок 1.

ы можем увидеть, что всего 4 способа, но два нижних неотличимы, так как молекулы 1 и 2 совершенно одинаковы, и соответствуют одному и тому же макроскопическому состоянию системы. Таким образом, мы имеем три различных макроскопических состояния системы, два из которых (верхних) , реализуемых только одним способом, а третье, нижнее двумя. Число способов-термодинамическая вероятность W. Все четыре способа равновероятны, поэтому большую часть времени система будет находиться в третьем состоянии.

Мы рассматривали только 2 молекулы. Число способов размещения n молекул в двух частях объема равно 2ⁿ, а число способов размещения всех молекул в одной половине объема равно 1. Энтропия термодинамического состояния системы определяется через термодинамическую вероятность:

S = k·lnW, где k – постоянная Больцмана. Данное выражение называется принципом Больцмана [2].

В статистической термодинамике энтропия так же характеризует меру беспорядка и хаоса.

2. Энтропия как мера степени неопределенности.

Существование неопределённости связано с участием вероятностей в осуществлении событий. Устранение неопределённости есть увеличение вероятности наступления того, что задано как цель. Поэтому вероятности должны участвовать в математической формулировке величины устранённой неопределённости.

Первая удачная попытка реализовать определение информации на такой основе осуществлена в 1928 г. Л. Хартли. Пусть возможно в данных условиях n вариантов некоторого результата. Целью является один из них. Хартли предложил характеризовать неопределённость логарифмом числа n [1].

Количественная мера s полученной информации (устранённой неопределённости)выражается логарифмом отношения вероятностей:

Есть один недостаток-это определение справедливо только в приближении равновероятности всех исходов. Это выполняется далеко не всегда. В пределе в этом определении невероятному исходу приравнивается неизбежный. В 1948 г. это исправил К. Шеннон.

В качестве меры априорной неопределенности системы (или прерывной случайной величины ) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

. (18.2.2)

Энтропия обладает рядом свойств, которые оправдывают выбор данного понятия в качестве характеристики степени неопределенности. Во-первых, обращение энтропии в нуль объясняется достоверностью состояния системы при других-невозможных. Во-вторых, энтропия о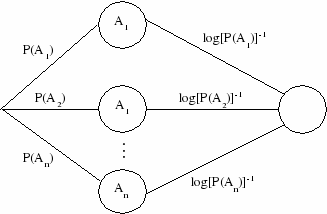бращается в максимум при равновероятности состояний, а при увеличении числа состояний - увеличивается. Главное: свойство аддитивности.

Энтропию дискретного опыта удобно находить как вес следую­щего графа:

Р

Рисунок 2.

еальная ценность понятия энтропии определяется в первую очередь тем, что выражаемая им «степень неопределенности» опытов оказывается во многих случаях именно той характеристикой, которая играет роль в разнообразных процессах, встречающихся в природе, обществе и технике и так или иначе связанных с передачей и хранением каких-либо сообщений.