2.2.3 Алгоритм обработки образов основанный на фильтрах Габора

Преимуществом данного метода является самое высокое качество обработки образов ОП из применяемых на сегодняшний день фильтров. Недостатком – самые высокие требования к вычислительной мощности из всех представленных алгоритмов.

Так как перед нами стоит задача выбрать алгоритм из условия качества фильтрации и сохранения ключевой информации, то наиболее рациональным выбором является алгоритм, основанный на фильтрах Габора, так как он лучше других удовлетворяет данным критериям.

2.3 Преобразование Габора

Рассмотри фильтр Габора в контексте нашей задач, а именно двумерный фильтр Габора.

2.3.1 Пространственный фильтра Габора для 2-Dизображений

Формула функции Габора выглядит следующим образом:

,

где - комплексная синусоида, а- огибающая Гаусса для двумерного пространства. Остановимся более подробно на этих составных частях фильтра Габора.

2.3.2 Комплексная синусоида

Комплексная синусоида определяется как

,

где и Р определяются как пространственная частота и фаза синусоиды.

Можно представить синусоиду как две действительные функции, расположенные в действительной и мнимой части комплексной функции (Рисунок 2.1).

Рис. 2.1. Действительная и мнимая часть комплексной синусоиды с параметрами: ,.

Действительная и мнимая части синусоиды имеют вид:

Параметры определяют частоту синусоиды в декартовых координатах.

2.3.3 Огибающая Гаусса

Огибающая Гаусса имеет вид:

,

где - координаты пика функции,а и b скалярные параметры Гауссиана, - индекс, обозначающий операцию вращения, такой, что:

.

Иллюстрация огибающей Гаусса представлена на рисунке 2.2.

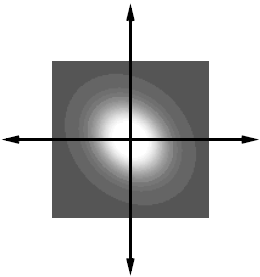
Рис.2.2. Огибающая Гаусса при значениях параметров:

2.3.4 Комплексная функция Габора

Комплексная функция Габора определяется следующими 9 параметрами:

• KВесовая величина огибающей Гаусса

• (a,b) Весовые величины огибающей, распределенные по осям

• Угол вращения огибающей Гаусса

• Координаты пика огибающей Гаусса

• Пространственные частоты комплексной синусоиды

• Р Фаза комплексной синусоиды

Каждая комплексная функция Габора состоит из двух частей, расположенных в действительной и мнимой части функции (Рисунок 2.3).

Рис.2.3 Действительная и мнимая часть комплексной функции Габора.

Таким образом, функция Габора имеет вид:

2.3.5 Алгоритм построения двумерного фильтра Габора

Для построения двумерного фильтра Габора применяется формула

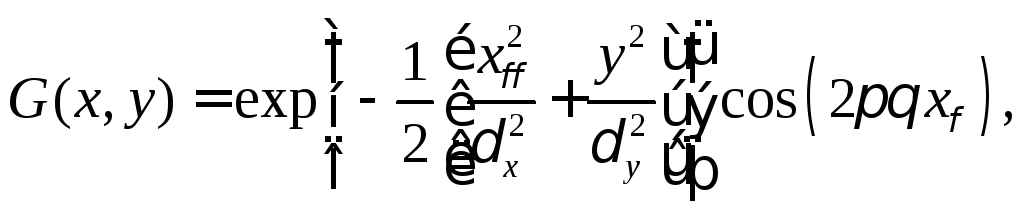
где ,;и- стандартные отклонения Гауссова ядра по осям соответственно, определяющая растянутость фильтра по осям;- частотная модуляция фильтра;- пространственное направление фильтра, определяющее ориентацию фильтра относительно осей xиy.

На Рисунке 2.4 изображена визуализация двумерной функции Габора в пространстве.

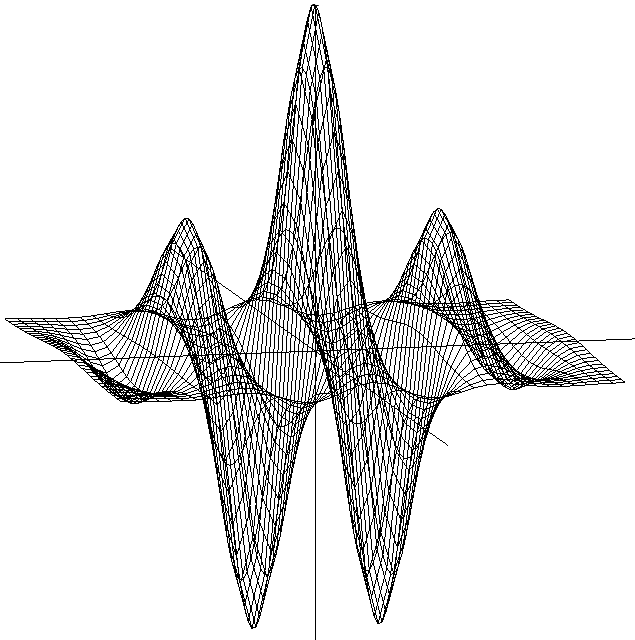
Рис.2.4. Двумерная функция Габора.

2.4 Применение фильтра Габора для 2-Dизображений

Применение фильтра Габора для изображений осуществляется за четыре этапа.

Этап 1. Нормализация изображения.

Нормализация изображения необходима для того, чтобы задать предварительные средние значения и отклонения. Нормализованное изображение Gопределяется какизображение, гдеG(i,j) – значение нормализованной яркости пикселя с координатами (i,j). Нормализованное изображение рассчитывается исходя из среднего и среднеквадратического отклонения исходного изображения:

,

где и- заданные значения среднего и среднеквадратичного отклонения соответственно,и- исходные значения среднего и среднеквадратичного отклонения, вычисляются по формулам:

,

На рисунке 2.5 приведен пример входного и нормализованного изображения

(а) (б)

Рис.2.5. Пример входного (а) и нормализованного (б) изображения образа отпечатка пальца.

Этап 2. Расчет ориентационного изображения.

Рассчитываем рассчитывается ориентационное изображение. Ориентационное изображение О представляет собой матрицу , в которой каждая компонента показывает локальную ориентацию (угол наклона в данной точке) линии с координатами .

.

Пример ориентационного изображения отпечатка пальца показан на Рисунке 2.6.

а) б)

Рис.2.6. Ориентационные изображения фрагментов отпечатка пальца. На рисунке а) изображен фрагмент центра, на рисунке б) фрагмент дельты.

Этап 3. Расчет частотного изображения.

Частотное изображение представляет собой матрицу размера , в которой каждая компонента показывает локальную частоту линий в данной точке, определяемую как частоту гребней , направленных вдоль ориентации выступа. В случае, если в какой-то точке невозможно определить четкую синусоидально-очерченную волну (например, из-за наличие особых точек в этих координатах), частота определяется как средняя величина частоты в соседних блоках.

Рис.2.7. Пример блоков, в которых невозможно четко определить четкую синусоидально-очерченую волну.

Рис.2.8. Волновое представление линий в ячейке

Расчет частоты в точке с координатой рассчитывается следующим образом: если – количество пикселей между двумя соседними гребнями в блоке размерностью , и центр блока – пиксель с координатами , то частота в данной точке будет рассчитываться как

Этап 4. Бинаризация изображения.

Изображение Bопределяется как изображение, если каждый пиксель принимает одно из двух возможных значений – нуля единицы. Единица соответствует гребню отпечатка, ноль – впадине:

,

где - порог маскирования, а- интенсивность пикселя изображения.

Этап 5. Применение к бинарному изображению фильтров Габора.

Фильтр настраивается на локальную ориентацию выступов, применяется к пикселям выступов и впадин изображения.

где ;;- ориентация фильтра Габора,- частота, аи- пространственные константы огибающей Гаусса вдоль осейxиyсоответственно.

Для использования Фильтра Габора нам необходимо знать значения следующих величин:

1) направление фильтра

2) частоту синусоидальной плоскостной волны

3) и- среднеквадратичные отклонения огибающей Габора

Частотная характеристика фильтра определяется из локальной частоты fвыступов, направление определяется локальной ориентацией. Значенияиможно задать при реализации алгоритма. Чем больше будут эти значения, тем более фильтр будет устойчив к шумам, но, в то же время, будет вносить больше искажений, создавая несуществующие выступы и впадины. Если выбрать значенияинизкими, фильтр не будет вносить искажений, но его способность фильтровать значительно снизится, что приведет к неэффективному устранению шумов. Поэтому при подборе значенийипытаются найти компромисс между эффективностью фильтра и отсутствием вносимых фильтром искажений. Как правило эти параметры подбираются эмпирическим путем.

Рис.2.9. Пример отпечатка пальца, обработанного фильтром Габора.