Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Уравнения в частных производных первого порядка (120

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

223.18 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

где f — произвольная функция, удовлетворяющая условию f(1) = 1.

Задача имеет бесчисленное множество решений, так как задан-

ная кривая — характеристика. Действительно, вектор ( ) =

F P,Q,R

= (x,y,2xy) вдоль заданной кривой принимает значения (x,x,2x2). Сама заданная кривая имеет вектор касательной (1,1,2x). Видно, что при любом x эти векторы коллинеарны.

В частном случае, когда в уравнении (1) R(x,y,u) = 0, уравнение

P(x,y,u)∂∂xu + Q(x,y,u)∂u∂y = 0

имеет очевидное решение: u = C1; это означает, что интегральные кривые характеристической системы этого уравнения лежат в горизонтальных плоскостях. В этом случае характеристикой принято называть проекцию интегральной кривой на плоскость (x,y). Во всех точках характеристики функция u принимает одинаковые значения. Геометрически это означает, что линии уровня функции u(x,y), являющейся решением уравнения, есть характеристики.

П р и м е р 6. Решить уравнение, описывающее простую волну (частный случай продольных колебаний стержня).

∂∂tε + a(ε)∂x∂ε = 0.

Р е ш е н и е. Характеристическая система имеет вид dt1 = adx(ε) = d0ε,

следовательно, ε = C1.

Заметим, что коэффициент a зависит не от t и x, а только от ε. Поскольку вдоль интегральных кривых ε постоянно, уравнение характеристик

dt = dx a(ε)

легко интегрируется, а сами характеристики

t − a(ε) = C2

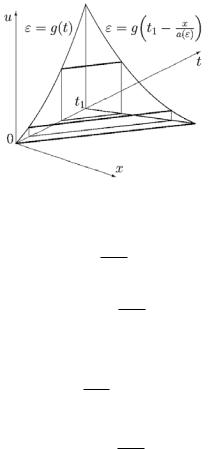
Рис. 7

— прямые в плоскости (x,y) (рис. 7). Следовательно,

Φ ε,t − a(xε) = 0,

или

ε = f t − a(xε) .

Произвольная функция f легко определяется, если при x = 0 задана функция ε = g(t):

f t − a(0ε) = g(t),

таким образом,

ε = g t − a(xε) .

На рис. 7 показаны интегральная поверхность, соответствующая найденному решению, и профиль волны для момента t = t1.

Приложение

ТИПОВОЙ РАСЧЕТ

Задача 1. Найти общее решение уравнения в частных производных первого порядка.

1.xy∂∂xu − x2 ∂u∂y = yu.

2.y∂∂xu = u.

3.(x + y2 + u2)∂∂xu + y∂u∂y = u.

4.(u2 − y2)∂∂xu + u∂u∂y + y = 0.

5.sin2 x∂∂xu + tgu∂u∂y = cos2 u.

6.	x	∂u	− u	∂u	= 0 (x > 0).

		∂x		∂y

7.y∂∂xu + u∂u∂y = xy.

8.2y4 ∂u∂x − xy∂u∂y = x√u2 + 1.

9.√x∂∂xu + √y∂∂yu = 12.

10.(u − y)2 ∂u∂x + xu∂u∂y = xy.

11.xy∂∂xu + (x − 2u)∂u∂y = yu.

12.(x2 + y2)∂∂xu + 2xy∂u∂y + u2 = 0.

13.2x∂∂xu + (y − x)∂u∂y − x2 = 0.

14.(xu + y)∂∂xu + (x + yu)∂u∂y = 1 − u2.

15.−x2 ∂u∂x + (xy − 2u2)∂∂yu = xu.

16.y∂∂xu + x∂u∂y = x − y.

17.xu∂x∂u + yu∂u∂y = xy√u2 + 1.

18.(x + u)∂∂xu + (y + u)∂u∂y = x + y.

19.x2u∂∂xu + y2u∂∂yu = x + y.

20.x∂∂xu + 2y∂u∂y = x2y + u.

21.ex ∂u∂x + y2 ∂u∂y = yex.

22.(u − y)∂∂xu + (x − u)∂u∂y + x − y = 0.

23.∂x∂u + (2y − u)∂u∂y = y + 2u.

24.yu∂∂xu − xu∂u∂y = eu.

25.(y3x − 2x4)∂∂xu + (2y4 − x3y)∂∂yu = 3u(x3 − y3).

26.(x + y)u∂∂xu + (x − y)u∂u∂y = y2 − 2xy − x2.

27.x2 ∂u∂x + (xyu − 2u2)∂∂yu = xu.

28.(u − 2x)∂∂xu + (ux + uy + 2x − u)∂u∂y = u.

29.(y + u)2 ∂u∂x − x(y + 2u)∂u∂y = xu.

	∂u		∂u	1
30. x						x2 + y2, где k — константа.
		+ y		=
	∂x		∂y		k

Задача 2. Решить уравнение в частных производных первого порядка при заданных дополнительных условиях.

1. x

∂u

+ y

∂u

= xy + u;

y =

u = x2.

∂x

∂y

2. x

∂u

−

∂u

= x2 + y2;

y = 1,

u = x2.

∂x

∂y

3. x

∂u

+ y

∂u

= u − xy;

x = 2, u = 1 + y2.

∂x

∂y

4. x

∂u

+ (y + x2)

∂u

= u;

u = y − 4,

x = 2.

∂x

∂y

5. xu

∂u

+ yu

∂u

= −xy;

y = x2,

u = x3.

∂x

∂y

6. x

∂u

+ y

∂u

= u − x2 − y2;

y = −2,

u = x − x2.

∂x

∂y

7. (y − u)

∂u

= x − y;

u = y = −x.

+ (u − x)

∂x

∂y

8. x

∂u

+ (xu + y)

∂u

= u;

x + y = 2u,

xu = 1.

∂x

∂y

9. (x − u)

∂u

= 2u;

x − y = 2, u + 2x = 1.

+ (y − u)

∂x

∂y

10. xy

3 ∂u

2 ∂u

+ x

= uy

;

x = −u ,

y = u .

∂x

∂y

11. y2

∂u

+ xy

∂u

= x;

x = 0,

u = y2.

∂y

∂x

12. y

∂u

+ x

∂u

= x2 + y2;

x = 2, u = 1 + 2y + 3y2.

∂x

∂y

13. y

∂u

− x

∂u

= y2 − x2;

y = a,

2u = (x + a)2, где a —

∂x

∂y

константа.

14. yu

∂u

+ x

∂u

= 0;

u = x2,

y = 1.

∂x

∂y

15. x

∂u

+ u

∂u

= 0;

= −y,

x = 1.

∂x

∂y

16. u(x + u)

∂u

− y(y + u)

∂u

= 0;

u = √

, x = 1.

∂x

∂y

17.

∂u

− xy

∂u

= 2xu;

x + y = 2, yu = 1.

∂x

∂y

18.

tgx

∂u

+ y

∂u

= u;

y = x,

u = x3.

∂y

∂x

19.

∂u

− y

∂u

= u2(x − 3y);

x = 1, yu + 1 = 0.

∂x

∂y

20.

∂u

+ u

∂u

= y;

= 2u, x = −3u.

∂x

∂y

21.

∂u

(y + 2u )

−

= x

;

x = u,

y = x .

∂x

∂y

22.

2 ∂u

∂u

= 0;

x − y = 0,

x − yu = 1.

+ yu

+ u

∂x

∂y

23.

∂u

+ y

∂u

= 2u;

y = u,

x = 1.

∂x

∂y

24.

∂u

− y

∂u

= x − y;

x = 1, u = y2 + 1.

∂x

∂y

25. yu

∂u

+ xu

∂u

= xy;

x = a,

y2 + u2 = a2, где a —

∂x

∂y

константа.

26.

1 ∂u

−

1 ∂u

;

x = y,

u = x2.

y ∂x

∂y

∂u

27.

2xu

+ 2yu

= u2 − x2 − y2;

x2 + y2 = 1, u = 0.

∂x

∂y

28.

∂u

+ y

∂u

= x2 + y2;

x = 1, u = y2 − 1.

∂x

∂y

29.

√

∂u

√

∂u

−

√

= 0;

x = 1, √

+ √

= 1.

∂y

∂x

√

30.

∂u

= u − c;

(x − a)

+ (y − b)

x = a +

∂x

∂y

(y − b)

+ (u − c)

где a,b,c,R — константы.

ЛИТЕРАТУРА

1.Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1965.

2.Степанов В.В. Курс дифференциальных уравнений. М.: Физматгиз, 1958.

3.Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.

4.Камке Э. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966.

5.Сборник задач по математике для втузов: Специальные разделы математического анализа / Под ред. А.В. Ефимова, Б.П. Демидовича. М.: Наука, 1986.

6.Котельникова Л.П., Паршев Л.П. Методические указания к домашнему заданию по уравнениям в частных производных. М.: Изд-во МВТУ им. Н.Э. Баумана, 1987.

7.Ганина Э.П., Котельникова Л.П., Паршев Л.П. Методические указания к решению задач по курсу «Уравнения математической физики». М.: Изд-во МВТУ им. Н.Э. Баумана, 1988.

	СОДЕРЖАНИЕ
1.	Квазилинейные уравнения в частных производных первого по-
рядка с двумя независимыми переменными . . . . . . . . . . . . . . . . . . . . . . .		3
2.	Системы обыкновенных дифференциальных уравнений . . . . . . . .	4
3. Характеристики квазилинейного уравнения в частных производ-
ных первого порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		7
4.	Интегрирование квазилинейного уравнения в частных производ-
ных первого порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		9
5.	Нахождение частного решения (задача Коши) . . . . . . . . . . . . . . . . . .	12
Приложение. Типовой расчет . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		23
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		27

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]