Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кабардино-Балкарский Государственный Университет им. Х. Бербекова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчетные задания (Кузнецов) / 10-Линейная алгебра

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

308.62 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Задача 5. Пусть x =(x1, x2 , x3 ). Являются ли линейными следующие

преобразования:

Ax =(6x1 −5x2 −4x3 , −3x1 −2x2 − x3 , x2 +2x3 ),


5.1. Bx =(6 −5x2 −4x3 ,		3x1 −2x2 − x3 , x2 +2),
Cx =(x34 , 3x1 −2x2 − x3 , x2 +2x3 ).
Ax =(5x1 −4x2 −3x3 , 2x1 − x2 , x2 +2),
5.2. Bx =(5x1 −4x2 −3x3 ,		0,		x24 +2x3 ),
Cx =(5x1 −4x2 −3x3 , 2x1 − x2 , x2 +2x3 ).
Ax =(4x1 −3x2 −2x3 , x1, x1 +2x24 +3x3 ),
5.3. Bx =(4x1 −3x2 −2x3 ,		x1,		x1 +2x2 +3x3 ),
Cx =(4x1 −3x2 −2x3 , x1, x1 +2x2 +3).
Ax =(3x1 +2x2 + x3 , x3 , 2x1 −3x2 −4x3 ),
5.4. Bx =(3x1 +2x2 + x3 ,		1,	2x1 −3x2 −4),
Cx =(3x1 +2x2 + x3 , x3 , 2x14 −3x2 −4x3 ).
Ax =(x1, x1 −2x2 −3, 4x1 −5x2 −6),
5.5. Bx =(x1,	x1 −2x2 −3x3 ,			4x14 −5x2 −6x3 ),
Cx =(x1, x1 −2x2 −3x3 , 4x1 −5x2 −6x3 ).
Ax =(2x1 + x2 , x2 −2x3 , 3x1 −4x22 −5x3 ),
5.6. Bx =(2x1 + x2 , x2 −2x3 ,				3x1 −4x2 −5x3 ),
Cx =(2x1 + x2 , x2 −2, 3x1 −4x2 −5).
Ax =(x1, x1 +2x2 +3x3 , 4x1 +5x2 +6x3 ),
5.7. Bx =(x1,	x1 +2x2 +3,		4x1 +5x2 +6),

Cx =(x1, x1 +2x2 +3x3 , 4x14 +5x2 +6x3 ).

Ax =(3x1 −2x2 − x3 , 1, x1 +2x2 +3),

5.8. Bx =(3x1	−2x2	− x3	,	0, x13 +2x2 +3x3 ),
Cx =(3x1 −2x2 − x3 ,				x3 , x1 +2x2 +3x3 ).

Ax =(2x1 − x2

5.9. Bx =(2x1 − x2

Cx =(2x1 − x2

,x3 , x1 +2x2 +3x34 ),

,x3 , x1 +2x2 +3x3 ),

,1, x1 +2x2 +3).

Ax =(x3 , 2x1 +3x2 +4x3 , 5x1 +6x2 +7x3 ),


5.10. Bx =(x3 ,	2x1 +3x2 +4,			5x1 +6x2 +7),
Cx =(x3 , 0, 5x14 +6x2 +7x3 ).
Ax =(6x1 −5x2 −4x3 , 3x1 −2x2 − x3 , 0),
5.11. Bx =(6x1 −5x2		−4,	3x1 −2x2 − x3 , 0),
Cx =(6x1 −5x2 −4x3 , 3x1 −2x2 − x32 , 0).
Ax =(5x1 −4x2 −3, 2x1 − x2 , x32 ),
5.12. Bx =(5x1 −4x2		−3x3 ,	2x1 − x2 , 1),
Cx =(5x1 −4x2 −3x3 , 2x1 − x2 , x3 ).
Ax =(4x1 −3x2 −2x3 , x12 , x2 +2x3 ),
5.13. Bx =(4x1 −3x2		−2x3 ,	x1,	x2 +2x3 ),
Cx =(4x1 −3x2 −2, x1, x2 +2).
Ax =(3x1 +2x2 + x3 , 0, x1 −2x2 −3x3 ),
5.14. Bx =(3x1 +2x2		+1, 0, x1 −2x2 −3),
Cx =(3x1 +2x2 + x3 , 0, x12 −2x2 −3x3 ).
Ax =(x1, x2 −2x3 , 3x1 −4x2 −5),
5.15. Bx =(x1,	x22 −2x3 ,		3x1 −4x2 −5),

Cx =(x1, x2 −2x3 , 3x1 −4x2 −5x3 ).

Ax =(2x1 + x2 , x32 , 2x1 −3x2 −4x3 ),

5.16. Bx =(2x1	+ x2 ,	x3 ,	2x1 −3x2 −4x3 ),
Cx =(2x1 + x2 , x3 , 2x1 −3x2 −4).
Ax =(x1, x2 +2x3 , 3x1 +4x2 +5x3 ),
5.17. Bx =(x1,	x2 +2x3 ,		3x1 +4x2 +5),
Cx =(x1, x22 +2x3 , 3x1 +4x2 +5x3 ).
Ax =(3x1 −2x2 −1, 0, x1 +2x2 +3x3 ),
5.18. Bx =(3x12 −2x2 − x3 ,			0,	0),
Cx =(3x1 −2x2 − x3 , 0, x1 +2x2 +3x3 ).
Ax =(2x12 − x2 , x3 , 2x2 +3x3 ),
5.19. Bx =(2x1 − x2 ,		x3 ,	2x2 +3x3 ),
Cx =(2x1 − x2 , x3 , 2x2 +3).
Ax =(0, x1 +2x2 +3x3 , 4x1 +5x2 +6x3 ),
5.20. Bx =(0,	x1 +2x2 +3x3 ,			4x1 +5x2 +6),
Cx =(0, x12 +2x2 +3x3 , 4x1 +5x2 +6x3 ).
Ax =(6x1 −5x2 −4x3 , 3x1 −2x2 − x3 , x2 ),
5.21. Bx =(6x1 −5x2 −4,			3x1 −2x2 − x3 , x2 ),
Cx =(6x1 −5x2 −4x33 , 3x1 −2x2 − x3 , 0).
Ax =(5x1 −4x2 −3, 2x1 − x2 , x1 +2x2 +3x3 ),
5.22. Bx =(5x1 −4x2 −3x33 ,			2x1 − x2 ,		x1 +2x2 +3x3 ),
Cx =(5x1 −4x2 −3x3 , 2x1 − x2 , x1 +2x2 +3x3 ).
Ax =(4x1 −3x23 −2x3 , x1 + x3 , 0),
5.23. Bx =(4x1 −3x2 −2x3 ,			x1 + x3 ,		2x1 +3x2 +4x3 ),

Cx =(4x1 −3x2 −2, x1 + x3 , 2x1 +3x2 +4x3 ).

Ax =(3x1 +4x2 +5x3 , 6x1 +7x2 +8x3 , 9x1 + x3 ),


5.24. Bx =(3x1 +4x2 +5,			6x1 +7x2 +8, 9x1 + x3 ),
Cx =(3x1 +4x2 +5x33 , 6x1 +7x2 +8x3 , 0).
Ax =(2x1 +3x2 +4, 5x1 +6x2 +7, 8x1 + x3 ),
5.25. Bx =(2x1 +3x2 +4x33 ,				5x1 +6x2 +7x3 ,			0),
Cx =(2x1 +3x2 +4x3 , 5x1 +6x2 +7x3 , 8x1 + x3 ).
Ax =(x13 + x3 , 2x1 +3x2 +4x3 , 0),
5.26. Bx =(x1 + x3 ,		2x1 +3x2 +4x3 ,				5x1 +6x2 +7x3 ),
Cx =(x1 +1, 2x1 +3x2 +4, 5x1 +6x2 +7x3 ).
Ax =(3x1 −2x2 − x3 , x2 +2x3 , 3x1 +4x2 +5x3 ),
5.27. Bx =(3x1 −2x2 −1,			x2 +2,		3x1 +4x2 +5x3 ),
Cx =(3x1 −2x2 − x33 , x2 +2x3 , 0).
Ax =(2x1 − x2 , x1 +2x2 +3, 4x1 +5x2 +6x3 ),
5.28. Bx =(2x1 − x23 ,		x1 +2x2 +3x3 ,				0),
Cx =(2x1 − x2 , x1 +2x2 +3x3 , 4x1 +5x2 +6x3 ).
Ax =(x13 +2x2 +3x3 , 4x1 +5x2 +6x3 , 7x1 +8x2 ),
5.29. Bx =(x1 +2x2 +3x3 ,				4x1 +5x2 +6x3 ,			7x1 +8x2 ),
Cx =(x1 +2x2 +3, 4x1 +5x2 +6, 7x1 +8x2 ).
Ax =(x2 +2x3 , 3x1 +4x2 +5x3 , 6x1 +7x2 +8x3 ),
5.30. Bx =(x2 +2,		3x1 +4x2 +5,			6x1 +7x2 +8x3 ),
Cx =(x23 +2x3 , 3x1 +4x2 +5x3 , 6x1 +7x2 +8x3 ).
Ax =(x12 ,	x1 − x3 ,		x2 + x3 ),
5.31. Bx =(1,	x1 − x3 ,		x2 + x3 ),
Cx =(x1,	x1 − x3 ,		x2 + x3 ).

Задача	6.	Пусть	x ={x1, x2 , x3},
Bx ={x2 , 2x3 ,	x1}. Найти:

6.1.ABx.

6.4.B4 x.

6.7.(A2 + B2 )x.

6.10. B(2A − B)x.

6.13. (A − B)2 x.

6.16. (3A2 + B)x.

6.19. (2B − A2 )x.

6.22. (A(B + A))x.

6.25. 2(B +2A2 + B2 )x.

6.28. (B(A + B))x.

6.31. (B(2A + B))x.

6.2. A2 x.

6.5. B2 x.

6.8. (B2 + A)x.

6.11. A(2B − A)x.

6.14. (B −2A2 )x.

6.17. (A2 + B)x.

6.20.B3 x.

6.23.(AB2 )x.

6.26. (B(A − B))x.

6.29. (A + BA − B)x.

Ax ={x2 − x3 , x1, x1 + x3},

6.3. (A2 − B)x.

6.6. (2A +3B2 )x.

6.9. BAx.

6.12. 2(AB +2A)x.

6.15. BA2 x.

6.18. (A2 − B2 )x.

6.21. (B2 −2A)x.

6.24. (A(B − A))x.

6.27.(B − A + B2 )x.

6.30.(3B +2A2 )x.

Задача 7. Найти матрицу в базисе (e′,										e′,		e′), где
								1		2		3
	e1′ = e1 −e2 +e3 , e2′ = −e1 +e2 −2e3 , e3′ = −e1 +2e2 +e3 ,
если она задана в базисе (e1, e2						, e3 ).
		1	0 2				2		1 0					0	2	3
7.1.		3	−1	0		7.2.		3		0	4		7.3.	4	1	0
7.1.		3	−1	0	.	7.2.		3		0	4	.	7.3.	4	1	0	.
		1	1 −2					1		−1 2				2	−1 −2
		1	1 −2					1		−1 2				2	−1 −2
		1	2	0			2 0				1			0	3	2
7.4.		3	0			7.5.		3		0	2		7.6.	2	1
7.4.		3	0	−1 .		7.5.		3		0	2	.	7.6.	2	1	−1 .
		2	1					−1 1			2			0	−1 2
		2	1	−1				−1 1			2			0	−1 2

	1		3		0
	2
7.7.	2		1 −1 .
	0		2		1
	0		2		1
		1		1		0
7.10.		0		−1	1
7.10.		0		−1	1		.
		2		3	1
		2		3	1
		1		2	1
7.13.		0		2		0
7.13.		0		2		0	.
		−1		1	1
		−1		1	1
		1		1	3
7.16.		1		0	1
7.16.		1		0	1	.
		2		0	1
		2		0	1
		2		0		0
7.19.		1		−1		1
7.19.		1		−1		1		.
		−1		2		1
		−1		2		1
		0		0		1
7.22.		2		1
7.22.		2		1		−1 .
		−1		1		1
		−1		1		1
		2		0	1
7.25.		0		1
7.25.		0		1	−1 .
		1		1
		1		1	−1
		2		1		0
7.28.		1		0	1
7.28.		1		0	1		.
		1		−1	1
		1		−1	1
		0		1		1
7.31.		−1		0
7.31.		−1		0		1 .
		1		−1
		1		−1		1

	2		1	2						0
	3		0	2						4
7.8.	3		0	2		.			7.9.	4
	1		0	1						−1
	1		0	1						−1
		2	1			1					3
7.11.		0	0			2			7.12.		1
7.11.		0	0			2		.	7.12.		1
		1	3								2
		1	3		−1						2
		1		1		2					1
7.14.		0		2		1			7.15.		2
7.14.		0		2		1		.	7.15.		2
		1	−1			0					0
		1	−1			0					0
		1		0		1					1
7.17.		0	−1			2			7.18.		3
7.17.		0	−1			2		.	7.18.		3
		3	−1			1					1
		3	−1			1					1
		1	1		0						0
7.20.		1	1		1				7.21.		1
7.20.		1	1		1		.		7.21.		1
		0	2		1						2
		0	2		1						2
		0		1		1					0
7.23.		0		2					7.24.		0
7.23.		0		2		1 .			7.24.		0
		−1		2							1
		−1		2		1					1
		2	0			1					2
7.26.		1	1			1			7.27.		−1
7.26.		1	1			1		.	7.27.		−1
		0	2								0
		0	2		−1						0
		2		1		0					2
7.29.		0		1					7.30.		−1
7.29.		0		1		−1 .			7.30.		−1
		−1		1		1					1
		−1		1		1					1

1	2
0	1
		.
−2	1

0	1
−1	0
			.
1
	−1

1 1

01 .

0		2
0		−1 .
−2		1
−2		1
1	1
1	0
1	0	.
1	1
1	1

32 .

1−1

1	−1
3	1
		.
1	0

−1		0
0		1
			.
1
	−1

Задача 8. Доказать линейность, найти матрицу, область значений и ядро оператора:

8.1.проектирования на ось Оx ;

8.2.проектирования на плоскость z = 0 ;

8.3.проектирования на ось Oz ;

8.4.зеркального отражения относительно плоскости Oyz ;

8.5.проектирования на ось Oy ;

8.6.проектирования на плоскость y = 0;

8.7.зеркального отражения относительно плоскости x − y = 0;

8.8.зеркального отражения относительно плоскости y + z = 0 ;

8.9.проектирования на плоскость y − z = 0 ;

8.10. проектирования на плоскость y = 3x ;

8.11.проектирования на плоскость Oyz ;

8.12.зеркального отражения относительно плоскости x − z = 0 ;

8.13.зеркального отражения относительно плоскости Oxy ;

8.14.поворота относительно оси Ox на угол π2 в положительном направлении;

8.15.проектирования на плоскость x − y = 0;

8.16.проектирования на плоскость y + z = 0 ;

8.17.зеркального отражения относительно плоскости x + y = 0;

8.18.зеркального отражения относительно плоскости y − z = 0 ;

8.19.проектирования на плоскость x + y = 0;

8.20.проектирования на плоскость x − z = 0 ;

8.21.зеркального отражения относительно плоскости x + z = 0 ;

8.22.поворота относительно оси Oz в положительном направлении на угол π2 ;

8.23. проектирования на плоскость 3y + z = 0 ;

8.24.зеркального отражения относительно плоскости Oxz ;

8.25.поворота в положительном направлении относительно оси Oy на угол π2 ;

8.26.проектирования на плоскость x + z = 0 ;

8.27. проектирования на плоскость	y + 3z = 0 ;
8.28. проектирования на плоскость	3x + z = 0 ;

8.29. проектирования на плоскость 3x + y = 0 ;

8.30. поворота относительно оси Oz в положительном направлении на угол π4 ; 8.31. проектирования на плоскость x − 3z = 0 ;

Задача 9. Найти собственные значения и собственные векторы матрицы.

	4			−2		−1
9.1.	−1			3
9.1.	−1			3		−1 .
	1			−2		2
	1			−2		2
	5			−1		−1
9.4.	0			4
9.4.	0			4		−1 .
	0			−1		4
	0			−1		4
	2			0		−1
9.7.	1			1
9.7.	1			1		−1 .
	−1			0		2
	−1			0		2
		5		1		−1
9.10.		2		4
9.10.		2		4		−1 .
		−2 1				6
		−2 1				6
		3		−2		2
9.13.		0		3		0
9.13.		0		3		0	.
		0		2		1
		0		2		1
		7		−6		6
9.16.		4		−1		4
9.16.		4		−1		4	.
		4		−2		5
		4		−2		5
		7		2		−	2

		3		3			3
		3		3			3
			4		5		2
9.19.			4		5	−	2	.
9.19.		3		3		−	3	.
		3		3			3
		0		0		1
		0		0		1

9.2.−11

9.5.−11

9.8. 1

−15

9.11. 2

9.14. 0

9.17. 2

9.20. 2

323

−1 0

−2 0 . 1 1

−2 −1 5 −1 .

−2 4

20 .

−4	4
1	2
		.
0	3

−2	2
5	0
		.
2	3

−6	6
3	2
		.
2	3


0			0
0			0
	7		−	4	.
3			−		.
3			3
−		2	5

		3	3
		3	3

9.3.00

9.6. 2

−24

9.9. 1

−13

9.12. 2

9.15. 2

9.18.62

9.21.1

−1 2

−1

−2 −1 −2

−4 3 0

−2

3 −23

−1 . 2

−1 −1 .

0 .

5.2

−2 −56 .

−43 . 11

	19 3			2 3	−2 3
9.22.		2		5	−2
9.22.		2		5	−2	.
		2 3 −2 3			11 3
		2 3 −2 3			11 3
		3	0	0
9.25.		1	2
9.25.		1	2	−1 .
		1	−1	2
		1	−1	2
		3		−2	−2
9.28.		−2 3		5 3	−2 3
9.28.		−2 3		5 3	−2 3	.
		−2 3		2 3	−13 3
		−2 3		2 3	−13 3
		7	−4 −2
9.30.		−2	5	−2
9.30.		−2	5	−2	.
		0	0	9
		0	0	9


	4			1 −1				2	1	−1
9.23		2		3	−2		9.24.	1	2
						.				−1 .
		1		−1 2				0	0
										1
	5 0 0							6	1 −1
9.26.			1	4			9.27.	2	5	−2
					−1 .						.
			1	−1 4				1	−1 4

	5 3	−2 3		−4 3
9.29.	0		1	0
9.29.	0		1	0	.
	−2 3		2 3	7 3
	−2 3		2 3	7 3
	4	−3	−3
9.31.	1	2	1
9.31.	1	2	1	.
	−1	1	2
	−1	1	2

Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа.

10.1.x12 +4x1x2 +4x1x3 +4x2 x3 +4x32 .

10.2.4x12 +4x1x2 +8x1x3 −3x22 +4x32 .

10.3.4x12 +8x1x2 +4x1x3 + x32 .

10.4.4x12 +8x1x2 +4x1x3 +3x22 −2x32 .

10.5.x12 +4x1x2 +4x1x3 +3x22 +4x2 x3 + x32 .

10.6.x12 +4x1x2 +4x2 x3 + x32 .

10.7.x12 +2x1x2 +2x1x3 −3x22 −6x2 x3 −2x32 .

10.8.x12 +4x1x2 +2x1x3 +3x22 +2x2 x3 + x32 .

10.9.x12 +4x1x3 − x22 −2x2 x3 +4x32 .

10.10.x12 +2x1x2 +2x1x3 + x32 .

10.11.x12 +4x1x2 +4x1x3 +8x22 +12x2 x3 +4x32 .

10.12.4x12 +4x1x2 +8x1x3 +5x22 +8x2 x3 +4x32 .

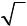
10.13.4x12 +8x1x2 +4x1x3 +8x22 +8x2 x3 + x32 .

10.14.4x12 +8x1x2 +4x1x3 +5x22 +8x2 x3 +4x32 .

10.15.x12 +4x1x2 +4x1x3 +5x22 +12x2 x3 +7x32 .

10.16.x12 +4x1x2 +4x1x3 +8x22 +16x2 x3 +7x32 .

10.17.x12 +2x1x2 +2x1x3 +5x22 +10x2 x3 +4x32 .

10.18.x12 +4x1x2 +2x1x3 +5x22 +6x2 x3 + x32 .

10.19.x12 +4x1x3 + x22 +2x2 x3 +4x32 .

10.20.x12 +2x1x2 +2x1x3 +2x22 +4x2 x3 + x32 .

10.21.x12 +4x1x2 +4x1x3 +4x2 x3 +2x32 .

10.22.4x12 +4x1x2 +4x1x3 −3x22 +2x32 .

10.23.4x12 +8x1x2 +4x1x3 + x32 .

10.24.4x12 +8x1x2 +4x1x3 +3x22 −4x32 .

10.25.x12 +4x1x2 +4x1x3 +3x22 +4x2 x3 − x32 .

10.26.x12 +4x1x2 +4x1x3 − x32 .

10.27.x12 +2x1x2 +2x1x3 −3x22 −6x2 x3 −4x32 .

10.28.x12 +4x1x2 +2x1x3 +3x22 +2x2 x3 − x32 .

10.29.x12 +4x1x2 − x22 −2x2 x3 +2x32 .

10.30.x12 +2x1x2 +2x1x3 − x32 .

10.31.x12 +2x1x2 +2x1x3 +2x22 +4x2 x3 +3x32 .

Задача 11. Привести квадратичную форму к каноническому виду ортогональным преобразованием.

11.1.	4x2	−3x2	+4x x		2	−4x x +8x x .
	2	3		1	2		1	3	2	3
11.2.	4x2	+4x2	+ x2	−2x x +2					3x x .
	1	2	3			1	2		2	3

11.3. 2x12 +2x22 +2x32 +8x1x2 +8x1x3 −8x2 x3.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в папке Расчетные задания (Кузнецов)

#
09.02.2015393.84 Кб1102-Дифференцирование.pdf
#
09.02.2015267.76 Кб1203-Графики.pdf
#
09.02.2015390.9 Кб1504-Интегралы.pdf
#
09.02.2015353.79 Кб1406-Ряды.pdf
#
09.02.2015291.1 Кб1109-Аналитическая геометрия.pdf
#
09.02.2015308.62 Кб1910-Линейная алгебра.pdf
#
09.02.2015255.41 Кб175-Дифур.pdf
#
09.02.2015294.84 Кб257-Кратные интегралы.pdf
#
09.02.2015340.12 Кб248-Векторный анализ.pdf