
Предварительные результаты
В этом разделе доказаны некоторые необходимые вспомогательные результаты.
Лемма
1.1. Пусть
 является частичной геометрией
является частичной геометрией .
Тогда
.
Тогда и выполняются следующие утверждения:
и выполняются следующие утверждения:
(1)
точечный граф
 является сильно регулярным с
является сильно регулярным с ,
,
 ,
и
,
и
 содержит
содержит прямых;
прямых;
(2)
 делит
делит (условие
целочисленности);
(условие
целочисленности);
(3) (s+1−2α)t ≤(s−1)(s+1−α)2 (условие Крейна);
(4)
если
 содержит подгеометрию
содержит подгеометрию ,
то
,
то или
или .
.
Лемма
1.2. Пусть
 является -однородной геометрией
является -однородной геометрией .
Тогда точечный граф
.
Тогда точечный граф является реберно регулярным с
является реберно регулярным с .
Кроме того,
.
Кроме того, делит
делит ,
и в случае
,
и в случае число
число четно.
четно.
Пусть
далее
 и
и является антифлагом с
является антифлагом с .
По структуре вычета
.
По структуре вычета для
для точка
точка лежит на
лежит на прямых в
прямых в ,
пересекающих
,
пересекающих ,
так что
,
так что содержит единственную точку
содержит единственную точку такую, что тройка
такую, что тройка не лежит ни в одном из блоков множества
не лежит ни в одном из блоков множества .
Ясно, что
.
Ясно, что ,
поэтому число
,
поэтому число четно.
четно.
Лемма
1.3. Пусть
 - сильно -однородная геометрия
- сильно -однородная геометрия ,
где
,
где .
Тогда точечный граф
.
Тогда точечный граф является псевдогеометрическим для
является псевдогеометрическим для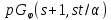 и имеет собственные значения
и имеет собственные значения .
.
Лемма
1.4. 3-однородное
расширение частичной геометрии
 не существует.
не существует.
Доказательство.
Пусть
 является точечным графом 3-однородной
геометрии
является точечным графом 3-однородной
геометрии .
Тогда
.
Тогда сильно регулярен с параметрами
сильно регулярен с параметрами Так как эта геометрия треугольная, то
подграф
Так как эта геометрия треугольная, то
подграф является треугольным графом T
является треугольным графом T для любого
для любого .
Значит, окрестности вершин в каждом
.
Значит, окрестности вершин в каждом -подграфе
графа
-подграфе
графа являются четырехугольниками, что
противоречит равенству
являются четырехугольниками, что
противоречит равенству .
Лемма доказана.
.
Лемма доказана.
2. Случай
Предположим,
что
 есть - однородное расширение частичной
геометрии порядка
есть - однородное расширение частичной
геометрии порядка ,
т. е.
,
т. е. .
Пусть
.
Пусть является дополнением к графу
является дополнением к графу
Лемма
2.1. Допустим,
что геометрия
 сильно -однородна. Тогда либо
сильно -однородна. Тогда либо и
и -квадратная
-квадратная решетка,
либо
решетка,
либо и
и является треугольным графом
является треугольным графом ,
где
,
где .
.
Доказательство.
По лемме 1.3 граф
 имеет собственное значение
имеет собственное значение ,
и по теореме Зейделя граф
,
и по теореме Зейделя граф является одним из следующих графов:
решетка или треугольный граф, полный
многодольный граф
является одним из следующих графов:
решетка или треугольный граф, полный
многодольный граф ,
граф Петерсена, Шрикханде, Чанга, Клебша
или Шлефли. Заметим,
,
граф Петерсена, Шрикханде, Чанга, Клебша
или Шлефли. Заметим, и
и
 ,
поэтому графы
,
поэтому графы
 исключаются.
исключаются.
Так
как граф Петерсена имеет параметры
 ,
то
,
то ,
противоречие с тем, что
,
противоречие с тем, что .
В случае графа Клебша граф
.
В случае графа Клебша граф имеет параметры (
имеет параметры ( противоречие с тем, что
противоречие с тем, что .
.
В
случае графа Шлефли граф
 имеет параметры
имеет параметры и
и ,
поэтому
,
поэтому ,
снова противоречие с тем, что
,
снова противоречие с тем, что .
.
Пусть
 имеет параметры решетки
имеет параметры решетки .
Тогда
.
Тогда .
Заметим, что граф Шрикханде имеет
параметры решетки при
.
Заметим, что граф Шрикханде имеет
параметры решетки при .
Но существует единственное расширение
обобщенного четырехугольника
.
Но существует единственное расширение
обобщенного четырехугольника с
с ,
и его точечный граф является дополнением
к
,
и его точечный граф является дополнением
к -решетке.
-решетке.
Пусть,
наконец,
 имеет параметры
имеет параметры треугольного графа. Тогда
треугольного графа. Тогда .
По условию Крейна для
.
По условию Крейна для имеем
имеем .
Будем считать, что
.
Будем считать, что .
Но тогда
.
Но тогда ,
, и графы Чанга
и графы Чанга не возникают.
не возникают.
Лемма
2.2. Пусть
 является -однородной геометрией
является -однородной геометрией с
с и
и делит
делит .
Тогда
.
Тогда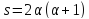 .
.
Доказательство.
Положим
 .
В случае
.
В случае имеем
имеем ,
и заключение леммы выполняется.
,
и заключение леммы выполняется.
По
лемме 1.1 число
 делится на
делится на .
Далее, числа
.
Далее, числа и
и взаимно просты, поэтому
взаимно просты, поэтому делит
делит .
Наконец,
.
Наконец, делит
делит и
и делит
делит .
.
Пусть
 .
Тогда
.
Тогда и
и ,
так что
,
так что ,
противоречие. Если
,
противоречие. Если ,
то
,
то ,
поэтому
,
поэтому и
и .
.
Поскольку
 ,
то
,
то и по условию целочисленности для
и по условию целочисленности для число
число делит
делит .
Значит,
.
Значит, ,
что противоречит условию леммы.
,
что противоречит условию леммы.
Лемма
2.3. Пусть
 является -однородной геометрией. Тогда
либо
является -однородной геометрией. Тогда
либо ,
либо
,
либо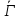 является сильно регулярным графом с
является сильно регулярным графом с и
и - геометрия
вершин и клик графа
- геометрия
вершин и клик графа
 ,
соответствующих
,
соответствующих для
для ,
либо
,
либо сильно однородна.
сильно однородна.
Доказательство.
Допустим, что
 - контрпример к этой лемме с минимально
возможным
- контрпример к этой лемме с минимально
возможным .
Имеем
.
Имеем ,
так что
,
так что .
Диаметр графа
.
Диаметр графа ограничен величиной
ограничен величиной ,
значит,
,
значит, .
.
По
выбору
 в ней найдутся точки
в ней найдутся точки на расстоянии 2 такие, что
на расстоянии 2 такие, что содержит блоки двух типов: блоки
содержит блоки двух типов: блоки с
с (
( -блоки)
и блоки
-блоки)
и блоки с
с (
( -блоки).
-блоки).
Пусть
 есть геометрия с точечным множеством
есть геометрия с точечным множеством и множеством блоков
и множеством блоков .
Тогда каждый блок из
.
Тогда каждый блок из ,
содержащий две точки
,
содержащий две точки и
и множества
множества ,
является
,
является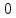 -блоком.
Таким образом, геометрия
-блоком.
Таким образом, геометрия сильно -однородна. Следовательно, либо
сильно -однородна. Следовательно, либо есть геометрия точек единственного
есть геометрия точек единственного -блока,
либо
-блока,
либо есть геометрия
есть геометрия для некоторого
для некоторого .
.
В
первом случае число точек в
 равно
равно .
Далее, каждый блок множества
.
Далее, каждый блок множества ,
содержащий точку из
,
содержащий точку из ,
содержит единственную точку из
,
содержит единственную точку из ,
поскольку
,
поскольку .
Так что число ребер между точками
множеств
.
Так что число ребер между точками
множеств и
и равно
равно .
Однако каждая точка геометрии
.
Однако каждая точка геометрии лежит в
лежит в блоках из
блоках из ,
содержащих поs
точек множества
,
содержащих поs
точек множества
 ,
поэтому то же число ребер равно
,
поэтому то же число ребер равно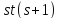 .
Значит,
.
Значит, (и этот случай не возникает в расширенном
четырехугольнике
(и этот случай не возникает в расширенном
четырехугольнике ).
).
В
случае
 имеется
имеется ребер между точками геометрии
ребер между точками геометрии и
и ,
поэтому
,
поэтому .
.
Допустим,
что выполняется первый случай. Тогда
 .
Пусть для
.
Пусть для точек
точек каждый блок множества
каждый блок множества является -блоком, и для
является -блоком, и для точек
точек все точки множества
все точки множества лежат в единственном
лежат в единственном -блоке.
Тогда число ребер между точками множеств
-блоке.
Тогда число ребер между точками множеств и
и равно
равно

Если
 ,
то по целочисленности числа точек в
множествах
,
то по целочисленности числа точек в
множествах и
и число
число делит
делит и
и ,
поэтому
,
поэтому .
Далее,
.
Далее, и
и делит
делит .
Так как
.
Так как взаимно
просты, то
взаимно
просты, то делит
делит .
Если
.
Если ,
то
,
то ,
если же
,
если же ,
то
,
то и
и .
Поэтому
.
Поэтому ,
противоречие.
,
противоречие.
Итак,
 ,
граф
,
граф разбивается на
разбивается на -блоки
и
-блоки
и Значит,
Значит, ,
, ,
поэтому граф
,
поэтому граф сильно регулярен с
сильно регулярен с ,
и
,
и является геометрией вершин и клик графа
является геометрией вершин и клик графа ,
соответствующих
,
соответствующих для
для .
Но это противоречит выбору
.
Но это противоречит выбору .
.
Таким
образом, мы доказали, что для любой точки

(1)
каждый блок из
 является -блоком или
является -блоком или
(2)
 содержит
подгеометрию
содержит
подгеометрию с точечным множеством
с точечным множеством и
множеством блоков
и
множеством блоков ,
причем
,
причем .
.
Пусть
 - множество точек графа
- множество точек графа ,
удовлетворяющее утверждению
,
удовлетворяющее утверждению .
Заметим, что если
.
Заметим, что если и точка
и точка лежит в
лежит в -блоке
-блоке из
из ,
то
,
то .
Следовательно,
.
Следовательно, разбивается на
разбивается на -однородные подгеометрии
-однородные подгеометрии .
По индукции мы заключаем, что либо
.
По индукции мы заключаем, что либо ,
либо эти подгеометрии сильно однородны,
и по лемме 2.1 имеем
,
либо эти подгеометрии сильно однородны,
и по лемме 2.1 имеем .
.
Как
и выше, у нас имеется равенство для
количества ребер между точками множеств
 и
и :
:

В
первом случае
 имеем
имеем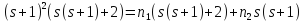 ,
поэтому
,
поэтому делит
делит .
Если
.
Если ,
что абсурдно. Значит,
,
что абсурдно. Значит, .
Так как
.
Так как разбивается на подгеометрии
разбивается на подгеометрии ,
то
,
то делит
делит ,
поэтому
,
поэтому делит 4 и
делит 4 и .
Противоречие с тем, что
.
Противоречие с тем, что не делит
не делит .
.
Предположим
теперь, что
 .
Тогдаt
.
Тогдаt и по утверждению (2) леммы 1.1 число
и по утверждению (2) леммы 1.1 число
 делитs
делитs ,
поэтому
,
поэтому
 делит
делит .
Далее,
.
Далее, делит
делит ,
поэтому
,
поэтому делит
делит .
Положим
.
Положим .
Тогда
.
Тогда делит
делит .
.
Если
 ,
то из равенства
,
то из равенства следует, что
следует, что ,
что противоречиво. Значит,
,
что противоречиво. Значит, иравенство
иравенство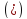 принимает вид:
принимает вид: .
Отсюда
.
Отсюда делит
делит делит (
делит ( .
Далее,
.
Далее, и
и .
Так как
.
Так как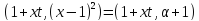 ,
то
,
то делит
делит ,
откуда
,
откуда
Если
 ,
то
,
то делит
делит ,
поэтому
,
поэтому не делит
не делит .
.
Если
 делит 4, и
делит 4, и .
Но тогда
.
Но тогда не делит
не делит .
Значит,
.
Значит, ,
противоречие с тем, что
,
противоречие с тем, что не делит
не делит .
.
Итак,
 ,
и по лемме 1.1 числоα
,
и по лемме 1.1 числоα делит
делит
 ,
поэтому
,
поэтому делит
делит .
Как и выше,
.
Как и выше, делит
делит ,
и по лемме 2.2 имеем
,
и по лемме 2.2 имеем .
.
Если
 ,
то ввиду равенства
,
то ввиду равенства имеем
имеем ,
что абсурдно. Значит,
,
что абсурдно. Значит, и согласно
и согласно число
число делит
делит .
Далее,
.
Далее, делит 7,
делит 7, делит 4 и
делит 4 и делит 2. Таким образом,
делит 2. Таким образом, делит 14, противоречие. Лемма 2.3 и теорема
1 доказаны.
делит 14, противоречие. Лемма 2.3 и теорема
1 доказаны.
