Решение типовых примеров

Пример 8.1. Пусть заданы законы распределения независимых дискретных случайных величин X и Y. Случайная величина Z определяется выражением .

Требуется найти математическое ожидание , дисперсию и среднее квадратическое отклонение случайной величины Z

x	−8	−4	−1	3		y	−2	1	3		A	−5/2
p	0.4	0.2	0.1	0.3		p	0.4	0.5	0.1		B	2/5

Решение.

Математическое ожидание заданных случайных величин и можно найти по формуле (8.1). В нашем случае

,

.

При вычислении дисперсий случайных величин X и Y воспользуемся универсальной формулой (8.4). Для этого составим законы распределения случайных величин и и вычислим математические ожидания и

	64	16	1	9			4	1	9
p	0.4	0.2	0.1	0.3		p	0.4	0.5	0.1

,

.

В результате дисперсия случайных величин X и Y запишется в виде

,

.

Для определения числовых характеристик случайной величины воспользуемся свойствами математического ожидания и дисперсии

,

.

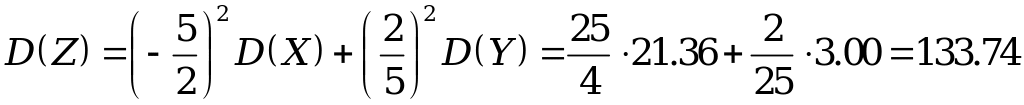При известной дисперсии среднее квадратическое отклонение определяется по формуле (8.3).

В нашем случае

.

Непрерывные случайные величины

Непрерывной называют случайную величину, все возможные значения которой сплошь заполняют некоторый конечный или бесконечный интервал числовой оси. Все возможные значения непрерывной случайной величины нельзя перечислить.

Примеры непрерывных случайных величин: а) длина ступни человека; б) диаметр ствола дерева; в) объем легких человека.

Функция и плотность распределения вероятностей непрерывной случайной величины

Функцией распределения (вероятностей) непрерывной случайной величины X называют функцию , равную для каждого действительного числа x вероятности того, что случайная величина X примет значение, меньшее x

.

Заметим, что наряду с термином «функция распределения (вероятностей)» часто используется термин «интегральная функция распределения».

Свойства функции распределения вероятностей

Свойство 1. Значения функции распределения вероятностей принадлежат отрезку : , причем , .

Свойство 2. Функции распределения вероятностей – неубывающая функция, т.е. если , то и наоборот.

Свойство 3. Вероятность того, что случайная величина X примет значение, принадлежащее интервалу , равна приращению функции распределения на этом интервале

.

Следствие. Вероятность того, что непрерывная случайная величина X примет одно конкретное значение равна нулю

.

Свойство 4. Если все возможные значения случайной величины X принадлежат интервалу , то

Плотностью распределения (вероятности) непрерывной случайной величины называют первую производную от функции распределения

.

Заметим, что наряду с термином «плотность распределения (вероятности)» часто используется термин «дифференциальная функция распределения». График функции называется «кривой распределения».