
- •Кинематическое исследование плоских шарнирно-рычажных механизмов
- •311300 “Механизация сельского хозяйства”, 311500 “Механизация переработки сельскохозяйственной продукции”, 311900 “Технология обслуживания и ремонта машин в апк” форм обучения
- •Введение
- •Принятые условные обозначения и их прочтение
- •Кинематический анализ механизмов
Принятые условные обозначения и их прочтение
А, В, С, D – точки А, В, С, D или кинематические пары А, В, С, D.
А' – скользящая, не зафиксированная точка на звене.
S3 – точка S, принадлежащая третьему звену.
АВ, ВСD – звенья.
ab – линия.
[AB] – отрезок, мм.
lАВ – длина звена, м.
VА – скорость точки А.
VBA – скорость точки В относительно точки А.
аB – ускорение точки В.
aBA – ускорение точки В относительно точки А.
![]() – нормальное
ускорение точки В относительно точки
С.
– нормальное
ускорение точки В относительно точки
С.
![]() – тангенциальное
ускорение точки В относительно точки
С.
– тангенциальное
ускорение точки В относительно точки
С.
[nВС] – отрезок в принятом масштабе, численно равный нормальному ускорению точки В относительно точки С.
[τВС] – отрезок в принятом масштабе, численно равный тангенциальному ускорению точки В относительно точки С.
![]() – вектор
ускорения точки Е в уравнении.
– вектор
ускорения точки Е в уравнении.
![]() – вектор
ускорения точки S4
на чертеже.
– вектор
ускорения точки S4
на чертеже.
![]() – угловое
ускорение звена АВ.
– угловое
ускорение звена АВ.
Кинематический анализ механизмов
Исследование начальных звеньев.
Кинематическое исследование механизма – это изучение движения звеньев механизма без учёта сил, обуславливающих это движение.
Если механизм имеет одну степень свободы, то перемещения, скорости и ускорения звеньев и точек механизма являются функциями перемещений, скоростей и ускорений начального звена.
Функция перемещений (закон движения начального звена) может быть задана в аналитической форме в виде функции, связывающей перемещение начального звена со временем. Если начальное звено входит во вращательную пару со стойкой, то задаётся функция φ = φ(t), где φ – угол поворота начального звена относительно неподвижной системы координат, связанной со стойкой, а t – время. Если начальное звено входит со стойкой в поступательную пару, то задаётся функция S = s(t), где S – перемещение произвольно выбранной точки начального звена относительно неподвижной системы координат, связанной со стойкой, а t – время.
Функции φ = φ(t) и S = s(t) могут также быть заданы графически в виде кривых, где по осям ординат отложены углы поворота φ или перемещения S, а по осям абсцисс – время. В некоторых задачах закон движения начального звена может быть задан в виде функций скоростей ω = ω(t) или V = v(t). Тогда переход от функции скорости к функциям перемещений может осуществляться путём интегрирования.
Если закон движения начального звена задан в виде функций ускорений ε = ε(t) или a = a(t), то переход к функциям скоростей, также осуществляется путём интегрирования, а определив функции скоростей, можно определить и функции положений.
Аналоги скоростей и ускорений.
При кинематическом исследовании механизмов скорости и ускорения звеньев и точек, им принадлежащих, удобно выражать в функции поворота или перемещения начального звена. Так если угол поворота какого-либо звена задан в виде функции φk = φk(φ), то угловая скорость этого звена может быть представлена как
![]() ,
,
где ω – угловая скорость начального звена, имеющая размерность с-1,
а
![]() – безразмерная величина угловой скорости
звена k,
которая называется аналогом угловой
скорости звена k.
Дифференцируя уравнение
– безразмерная величина угловой скорости
звена k,
которая называется аналогом угловой
скорости звена k.
Дифференцируя уравнение
![]() по времени t,
получим величину углового ускорения
εk
звена k:
по времени t,
получим величину углового ускорения
εk
звена k:
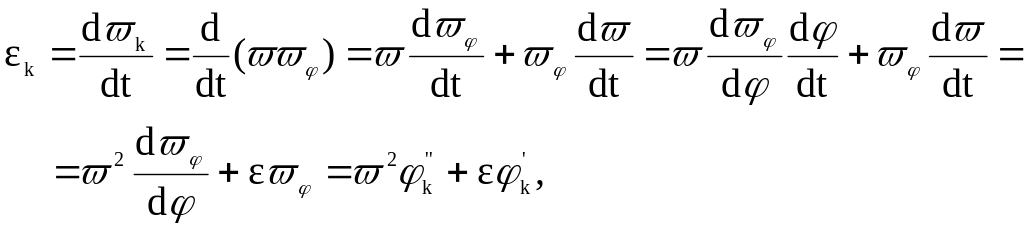
где
![]() - аналог углового ускорения звена k.
- аналог углового ускорения звена k.
Аналогично могут быть получены уравнения для скорости и ускорения какой-либо точки m звена k. Пусть rm – радиус-вектор, определяющий положение точки m. Продифференцировав его по времени, получим скорость и ускорение точки m:
![]() ,
,
где ω – угловая скорость начального звена, имеющая размерность с-1,
а
![]() есть аналог скорости Vφ
точки m.
есть аналог скорости Vφ
точки m.
Дифференцируя
уравнение
![]() по времени t,
получим величину ускорения am
точки m.
Ускорение аm
в общем случае состоит из четырёх
составляющих: нормального ускорения,
направленного вдоль радиуса вектора
rm
к его началу, тангенциального ускорения,
направленного перпендикулярно
радиусу-векто-ру rm,
релятивного (относительного) ускорения
вдоль радиуса-вектора rm
и наконец, кориолисова ускорения,
направленного перпендикулярно
радиусу-вектору rm.
по времени t,
получим величину ускорения am
точки m.
Ускорение аm
в общем случае состоит из четырёх
составляющих: нормального ускорения,
направленного вдоль радиуса вектора
rm
к его началу, тангенциального ускорения,
направленного перпендикулярно
радиусу-векто-ру rm,
релятивного (относительного) ускорения
вдоль радиуса-вектора rm
и наконец, кориолисова ускорения,
направленного перпендикулярно
радиусу-вектору rm.
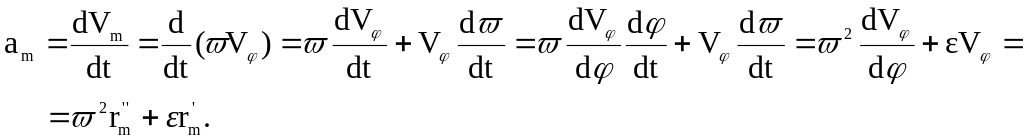
В последнем уравнении ω и ε – угловые скорость и ускорение начального звена. Величины ω2 и ε, входящие в уравнение, имеют размерность с-2. Величина аналога скорости Vφ имеет размерность длины.
Таким образом, скорости и ускорения звеньев и их точек могут быть всегда выражены через соответствующие аналоги скоростей и ускорений и угловые скорость и ускорение начального звена механизма. Если закон движения начального звена задан в виде функции S = s(φ), где S – линейное перемещение начального звена, то нахождение аналогов скоростей и ускорений может быть сделано аналогично.
Данный метод весьма сложный и трудоёмкий для выполнения его вручную, поэтому студенту предлагается освоение и использование программы APM WinSlider – приложение пакета АРМ WinMachine. APM WinSlider – это система, предназначенная для расчета сложных многозвенных рычажных механизмов первого и второго класса и визуализации движения их составляющих (звеньев, тел и кинематических пар). Система разработана центром разработки программного и научного обеспечения "Автоматизированное Проектирование Машин".
При помощи этой системы могут быть рассчитаны наиболее часто встречающиеся типовые плоские механизмы второго класса:
· четырехзвенники;
· кривошипно-ползунные механизмы;
· кулисные механизмы;
и механизмы на их основе.
В этой системе не предусмотрен расчет пространственных механизмов, мальтийских механизмов, фрикционных и храповых механизмов, а также механизмов со степенью свободы больше 1.
Даная система позволяет получить следующие параметры. 1. Траектории движения любых точек механизма. 2. Абсолютные и относительные значения линейных и угловых скоростей. 3. Аналоги угловой скорости и углового ускорения. Кроме этого, она позволяет получить значения траекторий, скоростей и ускорений в проекциях на оси Х и Y. Результаты расчётов выдаются в табличной и графической форме с возможностью их печати на принтере.
При изучении движения звеньев механизма составляют кинематическую схему механизма, которая является его кинематической моделью. Далее кинематическая схема строится с точным соблюдением всех размеров и форм, от которых зависит движение того или иного звена, другими словами, с соблюдением тех размеров и форм, при изменении которых изменяются положения, скорости и ускорения точек механизма.
Для определённости движений всех звеньев механизма, образованного кинематической цепью с одной степенью свободы, необходимо и достаточно иметь заданным закон движения одного из звеньев, являющегося ведущим.
Процесс образования механизма можно представить как последовательное присоединение к механизму первого класса (стойка и кривошип или стойка и ползун) кинематической цепи с нулевой степенью свободы относительно ведущего механизма. Например, при присоединении к стойке и входному звену двухповодковой группы получим шарнирный четырёхзвенник, обладающий одной степенью свободы. Аналогична последовательность построения любого механизма с одной степенью свободы: у него должно быть неподвижное звено (стойка), входное звено и одна или несколько кинематических цепей с нулевой степенью свободы относительно ведущего механизма. Такая последовательность построения и предусмотрена программой: устанавливается неподвижное звено, ведущее звено и вводятся параметры начального звена (закон движения) и наконец, рисуются кинематические цепи с нулевой степенью свободы относительно ведущего механизма.
Рекомендуется за начальное положение выбирать такое положение механизма, при котором выходное звено находится в любом из двух крайних положений.
Рассмотрим два примера исследования методом плана скоростей и ускорений для двух шарнирно-рычажных механизмов.
При кинематическом исследовании механизмов решаются следующие задачи. 1. Определяются траектории движения заданных точек механизма. 2. Определяются скорости этих точек. 3. Определяются их ускорения.
Для механизмов II класса, образованных последовательным присоединением структурных групп II класса к ведущему механизму, будем считать известными угловую скорость ведущего звена и длины всех звеньев. Исследование можно проводить аналитическим и графическим методами. Мы рассмотрим графический метод – метод плана скоростей и ускорений.
Пример 1.
Пусть задан пятизвенный механизм, состоящий из кривошипа ОА – звено 1,
ш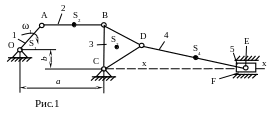 атуна
АВ – звено 2, коромысла ВDC
– звено 3, шатуна DE
– звено 4 и ползуна – звено 5. Механизм
установлен на неподвижной раме – звено
0. Кривошип ОА (рис.1) вращается с постоянной
угловой скоростью ω1
= 10 с-1.
Точки S2
и S4
находятся в центре звеньев АВ и DE.
Точка S3
находится на пересечении медиан.
атуна
АВ – звено 2, коромысла ВDC
– звено 3, шатуна DE
– звено 4 и ползуна – звено 5. Механизм
установлен на неподвижной раме – звено
0. Кривошип ОА (рис.1) вращается с постоянной
угловой скоростью ω1
= 10 с-1.
Точки S2
и S4
находятся в центре звеньев АВ и DE.
Точка S3
находится на пересечении медиан.
Дано:
ω1 = 10 с-1;
lOА = 0,1 м;
lAB = 0,179 м;
lBC = lBD = lCD = 0,127 м;
lDE = 0,306 м.
Найти:
Скорости и ускорения точек A, B, D, E, S2, S3, S4. Определить угловые скорости и угловые ускорения звеньев АВ, BCD, DE.
Решение:
. Определяем окружную скорость точки А, принадлежащей кривошипу и
шатуну:
![]() м/с.
м/с.
Теперь можем приступать к построению плана скоростей.
1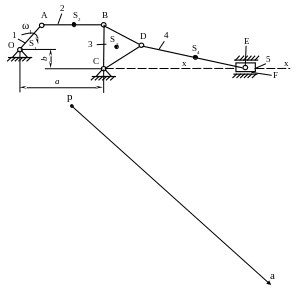 .2.
В произвольном месте чертежного листа
ставим точку p
– полюс скоростей. Из полюса проводим
вектор скорости точки А произвольной
длины по направлению, перпендикулярному
звену ОА, как показано на рис.2.
.2.
В произвольном месте чертежного листа
ставим точку p
– полюс скоростей. Из полюса проводим
вектор скорости точки А произвольной
длины по направлению, перпендикулярному
звену ОА, как показано на рис.2.
Рис.2
1.3. Определяем масштаб плана скоростей:
![]() м·с-1/мм,
м·с-1/мм,
где [pa] – длина вектора скорости точки А, мм.
1.4. Определяем скорость точки В. Точка В принадлежит и шатуну АВ,
и коромыслу ВСD. Её скорость может быть представлена как векторная сумма скоростей: переносной скорости VA и относительной скорости точки В относительно А , то есть VBA. С другой стороны, коромысло ВСD совершает колебательные движения относительно неподвижной точки С. Значит точка В имеет окружную скорость VВ , перпендикулярную ВС и переносную скорость точки С – скорость VC. Таким образом, мы можем получить систему векторных уравнений:
![]()
Эту систему можно решить графически.
1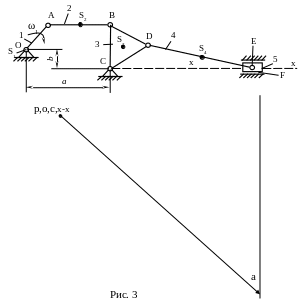 .4.1.
Вектор скорости VA
у нас уже есть. Линия действия вектора
скорости VBA
перпендикулярна шатуну АВ, а его
направление пока неизвестно, но поскольку
мы его прибавляем к вектору скорости
VA,
то известно, что он проходит через конец
вектора
.4.1.
Вектор скорости VA
у нас уже есть. Линия действия вектора
скорости VBA
перпендикулярна шатуну АВ, а его
направление пока неизвестно, но поскольку
мы его прибавляем к вектору скорости
VA,
то известно, что он проходит через конец
вектора
![]() (рис. 3).
(рис. 3).
1.4.2.
Решаем второе уравнение системы. Вектор
VC
= 0 значит,
построение VBC
начинаем из полюса p.
Вектор скорости VBC
направлен перпендикулярно грани ВС
звена ВСD.
Проводим его до пересечения с линией
действия скорости VBA,
как показано на рис. 4, получаем вектор
![]() .
Вектор
показывает величину
и направление скорости точки В –
скоростьVB.
.
Вектор
показывает величину
и направление скорости точки В –
скоростьVB.
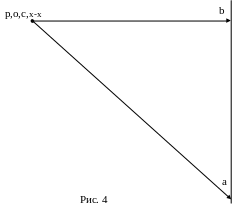
Получили
векторный треугольник или план скоростей
для ведущего механизма I(0,1)
и присоединённой к нему структурной
группы II
класса 1 вида 2 порядка – II(2,3).
Вектор
![]() показывает скорость
точки В относительно точки А. Вектор
показывает скорость
точки В относительно точки А. Вектор
![]() показывает скорость точки А относительно
точки В.
показывает скорость точки А относительно
точки В.
1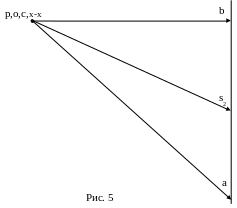 .5.
Множество векторов, проведённых из
полюса р на линию аb
будут показывать скорости точек,
принадлежащих звену АВ. Так если точка
S2
находится в центре звена АВ, то вектор,
проведённый из p
на середину линии аb
покажет скорость точки S2
(рис. 5).
.5.
Множество векторов, проведённых из
полюса р на линию аb
будут показывать скорости точек,
принадлежащих звену АВ. Так если точка
S2
находится в центре звена АВ, то вектор,
проведённый из p
на середину линии аb
покажет скорость точки S2
(рис. 5).
Вообще
точка S2
может находиться в любом месте на звене
АВ, тогда положение вектора
![]() можно определить отрезком [bs2].
Длину отрезка [bs2]
определим из отношений:
можно определить отрезком [bs2].
Длину отрезка [bs2]
определим из отношений:
![]() мм.
мм.
1.6.
Контур звена СВD
сохраняет своё подобие и на плане
скоростей. Так при обходе по часовой
стрелке СВD~cbd,
получаем вектор
![]() – вектор
ускорения точки В (рис. 6).
– вектор
ускорения точки В (рис. 6).
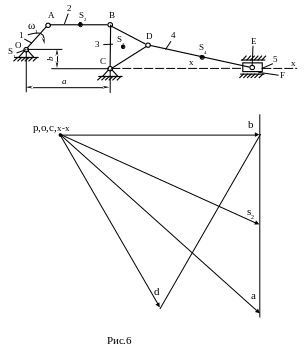
1.7. Точка S3 также сохраняет подобие своего расположения.
На плане скоростей точка s3 расположена на пересечении медиан в Δсbd (рис. 7).
Вектор
![]() показывает скорость
и направление движения этой точки.
показывает скорость
и направление движения этой точки.
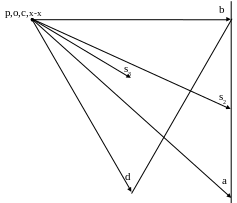
Рис.7.
1.8. Следующая структурная группа относится ко II классу 2 вида 2 порядка – II(4,5). Скорость точки Е – VE определим, рассуждая так же, как в пункте 1.4, сложением переносной и относительной скоростей VD и VED. С другой стороны, скорость VE равна сумме переносной скорости неподвижного звена Vx-x и относительной скорости точки Е – VEx-x. Таким образом, можно составить систему векторных уравнений и, решая её графически, получить скорость точки Е.
![]()
1.8.1. Решаем первое уравнение. Скорость точки D – VD у нас уже показана на плане скоростей вектором . Прибавляем к нему вектор скорости VED. Для этого через конец вектора проводим перпендикулярно звену DE линию действия скорости VED (рис. 8).
1.8.2.
Решаем второе векторное уравнение.
Скорость Vx-x
= 0, поэтому построение ведём из полюса
р. Скорость точки Е относительно
неподвижного звена Vx-x
направлена параллельно x-x.
Проводим вектор
![]() до пересечения с
линией действия скорости VED.
до пересечения с
линией действия скорости VED.
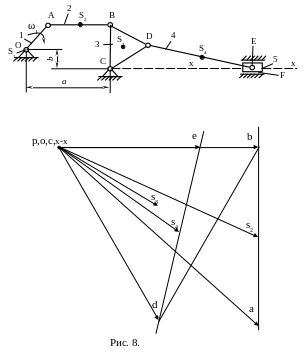
Вектор
![]() показывает скорость
точки Е относительно точки D.
Вектор
показывает скорость
точки Е относительно точки D.
Вектор
![]() показывает скорость
D
относительно Е.
показывает скорость
D
относительно Е.
1.9 Множество векторов, проведённых из полюса р на линию еd, покажут абсолютные скорости точек, принадлежащих звену ЕD. Если точка S4 находится в середине звена ЕD, то вектор, проведённый из полюса р на середину [ed], покажет скорость VS4 и направление её движения. Точка S4 может находиться в любом месте звена DE, тогда её положение на плане скоростей будет определено отрезком [es4]. Длину отрезка [es4] найдём из соотношения:
![]() мм.
мм.
1.10. Определяем численные значения скоростей VB, VD, VE,VBA, VDE, VS2, VS3, VS4.
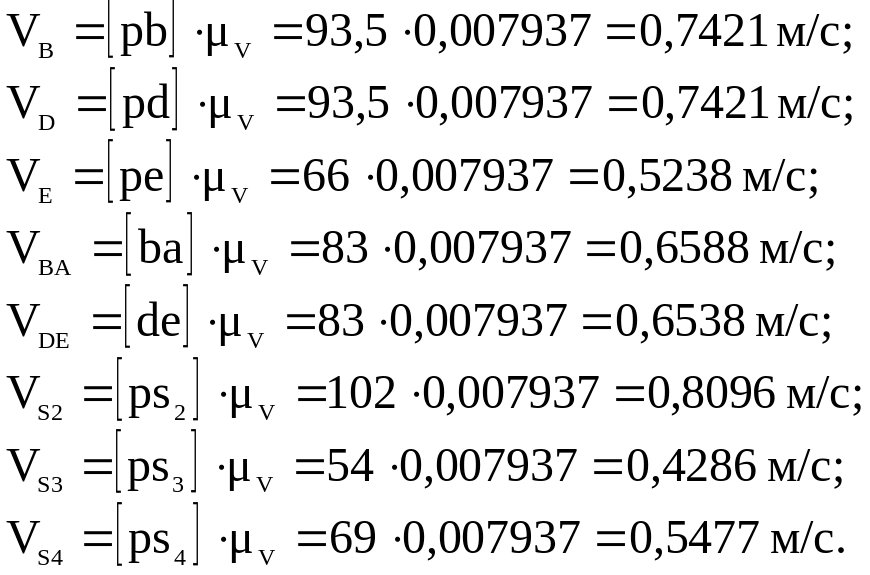
1.11. Находим угловые скорости звеньев AB, BCD, DE.
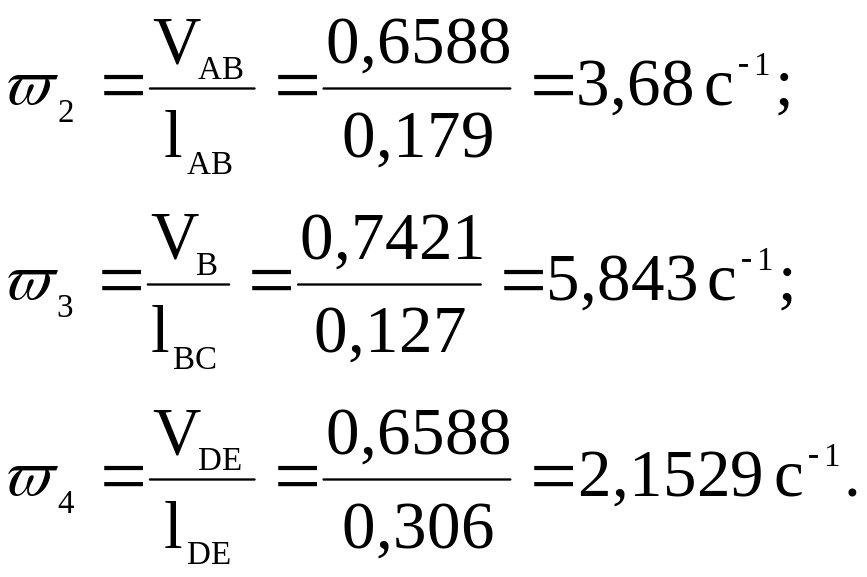
1.12. Построение плана ускорений.
Построение плана ускорений начинаем, также как и построение плана скоростей, с ведущего звена ОА. Кривошип ОА вращается с постоянной угловой скоростью, поэтому его угловое ускорение ε1 = 0, но есть центробежное ускорение
![]() .
.
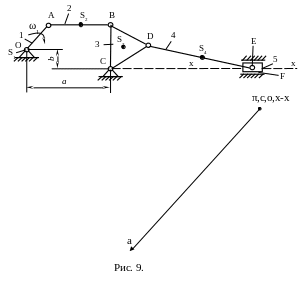
1.13.
В произвольном месте листа ставим полюс
ускорений – точку π. Из полюса проводим
вектор центробежного (нормального)
ускорения точки А произвольной длины
![]() .
Его направление параллельно звену ОА
(рис. 9).
.
Его направление параллельно звену ОА
(рис. 9).
Определяем масштаб ускорений:
![]() .
.
1.14.
Ускорение точки В будет состоять из
переносного ускорения точки А, нормального
![]() и тангенциального
и тангенциального
![]() ,
поскольку звено АВ совершает сложное
движение с поворотом. Так как точка В
принадлежит и звену СВD,
то её ускорение можно получить, как
переносное от точки С, а оно равно 0, плюс
нормальное
,
поскольку звено АВ совершает сложное
движение с поворотом. Так как точка В
принадлежит и звену СВD,
то её ускорение можно получить, как
переносное от точки С, а оно равно 0, плюс
нормальное
![]() и плюс тангенциальное
и плюс тангенциальное
![]() .
Получаем векторную систему уравнений:
.
Получаем векторную систему уравнений:
![]()
1.15. Определяем нормальные ускорения.
![]()
1.16. Решаем графически векторную систему уравнений.
1.16.1.
Ускорение aA
у нас уже изображено вектором
.
Через конец вектора
проводим вектор
![]() параллельно звену АВ по направлению от
В к А.
параллельно звену АВ по направлению от
В к А.
1.16.2. Длина вектора в принятом масштабе
![]()
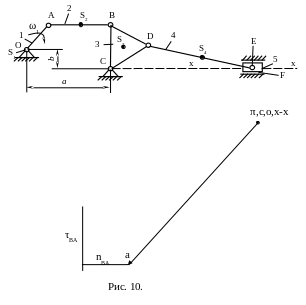
1.16.3.
Через конец вектора
проводим линию действия вектора ускорения
![]() с направлением, перпендикулярным к
звену АВ (рис. 10).
с направлением, перпендикулярным к
звену АВ (рис. 10).
1.16.4.
Решаем второе уравнение. Поскольку
ускорение точки С равно 0, то построение
начинаем из полюса π. Вектор
![]() направлен параллельно ВС от В к С. Длина
вектора
в принятом масштабе:
направлен параллельно ВС от В к С. Длина
вектора
в принятом масштабе:
![]()
1.16.5.
Через конец отрезка
проводим вектор ускорения
![]() по направлению, перпендикулярному
стороне ВС звена ВСD
до пересечения с линией действия вектора
ускорения
.
В точку пересечения из полюса проводим
вектор полного ускорения точки В –
по направлению, перпендикулярному
стороне ВС звена ВСD
до пересечения с линией действия вектора
ускорения
.
В точку пересечения из полюса проводим
вектор полного ускорения точки В –
![]() .
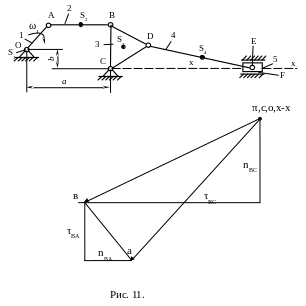
В масштабе
.
В масштабе
![]() вектор
показывает
направление и величину полного ускорения
точки В (рис. 11).
вектор
показывает
направление и величину полного ускорения
точки В (рис. 11).
1.17.
Вектор
будет показывать
ускорение точки В относительно А. Вектор
покажет ускорение
точки А относительно В. Множество
векторов, проведённых из полюса π на
линию аb,
покажут ускорения точек, принадлежащих
звену АВ. Если точка S2
расположена в середине звена АВ, то
вектор, проведённый из полюса π на
середину [аb]
– вектор
![]() покажет полное
ускорение
покажет полное
ускорение
![]() (рис. 12).
(рис. 12).

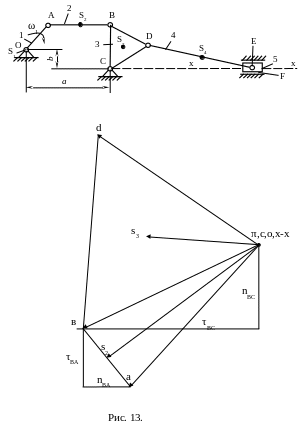
1.18.
Контур звена СВD
также, как и на плане скоростей, сохраняет
своё подобие и на плане ускорений. Так
при обходе по часовой стрелке СВD~сbd.
Получили вектор ускорения точки D
– вектор
![]() (рис. 13). Точка s3
находится на пересечении медиан в
треугольнике cbd.
(рис. 13). Точка s3
находится на пересечении медиан в
треугольнике cbd.
1.19. Следующая структурная группа состоит из звеньев 4 и 5. Для определения ускорений этой структурной группы имеем систему уравнений:
![]()
Так
как ось x-x
направляющей неподвижна, то ускорение
![]() и кориолисово ускорение
и кориолисово ускорение
![]() равны 0. Тогда система уравнений для
определения ускорений звеньев 4 и 5 будет
иметь вид
равны 0. Тогда система уравнений для
определения ускорений звеньев 4 и 5 будет
иметь вид
![]()
1.20.
Определяем нормальное ускорение
![]() .
.
![]() м/с2.
м/с2.
1.21. Решаем графически векторную систему уравнений.
1.21.1. Длина вектора ускорения в принятом масштабе
![]()
1.21.2.
Через конец вектора
![]() проводим параллельно
звену DE
вектор
проводим параллельно
звену DE
вектор
![]() по направлению от Е к D.
Через конец вектора
проводим линию действия ускорения
по направлению от Е к D.
Через конец вектора
проводим линию действия ускорения
![]() перпендикулярно звену ЕD
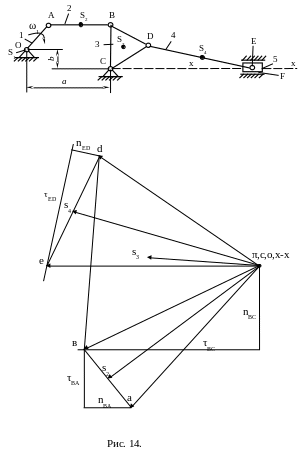
(рис. 14).
перпендикулярно звену ЕD
(рис. 14).
1.21.3.
Из второго уравнения имеем условие, при
котором ускорение точки Е равно
релятивному ускорению Е относительно
неподвижной направляющей вдоль оси
x-x.
Проводим из полюса вектор
![]() до пересечения с линией действия
ускорения
,
как показано на рис. 14.
до пересечения с линией действия
ускорения
,
как показано на рис. 14.
1.21.4. Множество векторов, проведённых из полюса π на линию еd, покажут ускорения точек, принадлежащих звену ЕD. Если точка S4 расположена в середине звена ЕD, то вектор, проведённый из полюса π на середину [ed] – вектор , покажет полное её ускорение.
1.22. Из полученного плана ускорений определяем значения ускорений точек B, D, E, S2, S3, S4, E.
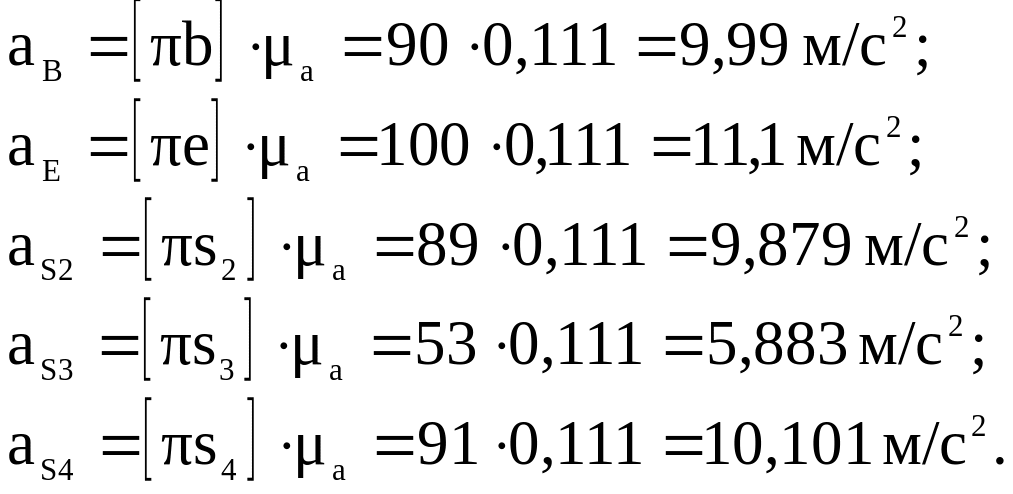
1.23. Определяем значения тангенциальных ускорений.
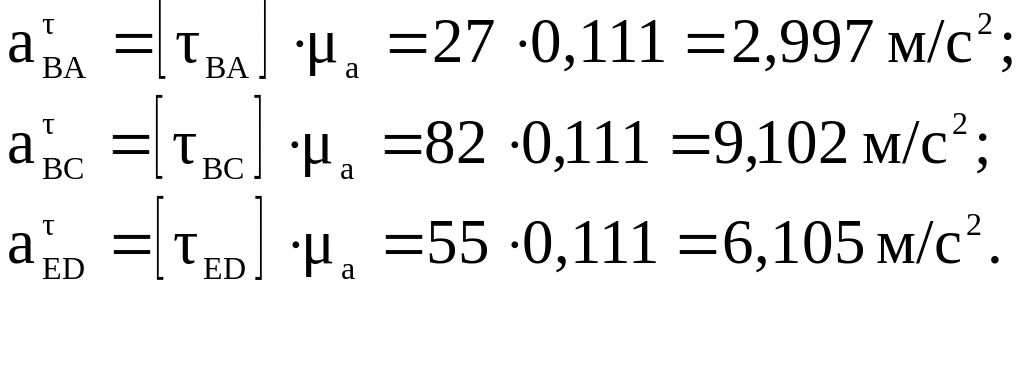
1.24. Определяем угловые ускорения звеньев АВ, BCD, DE.
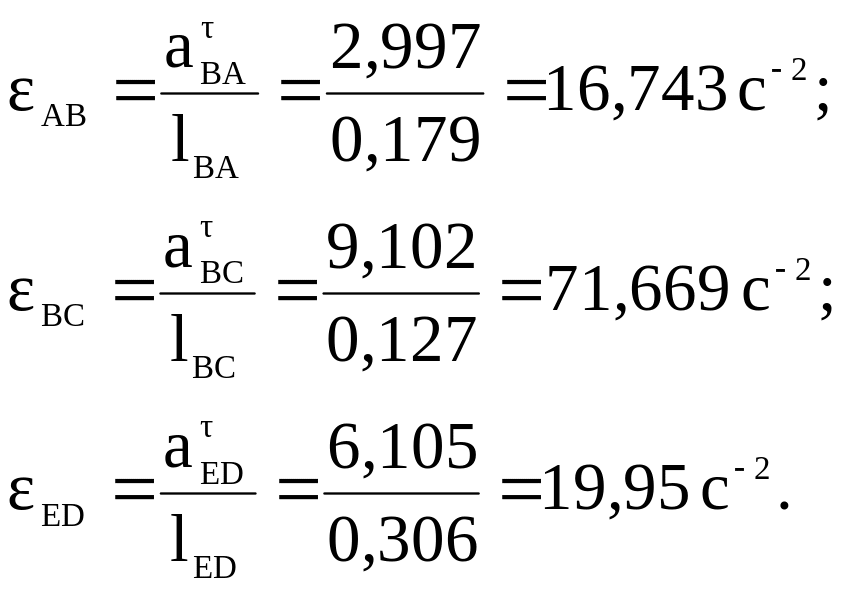
Пример 2.
Пусть задан пятизвенный механизм, состоящий из кривошипа ОА – звено 1,
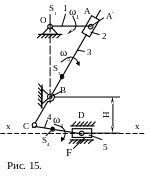 кулисного
камня – звено 2, кулисы CВА'
– звено 3, шатуна CD
– звено 4 и ползуна – звено 5. Механизм
установлен на неподвижной раме – звено
0. Кривошип ОА (рис.1) вращается с постоянной
угловой скоростью ω1
= 10 с-1.
Положение точки S3
определено отрезком [BS3]
так, что [BS3]
= 0,733·[CB].
Точка S4
находится в центре звена CD.
кулисного
камня – звено 2, кулисы CВА'
– звено 3, шатуна CD
– звено 4 и ползуна – звено 5. Механизм
установлен на неподвижной раме – звено
0. Кривошип ОА (рис.1) вращается с постоянной
угловой скоростью ω1
= 10 с-1.
Положение точки S3
определено отрезком [BS3]
так, что [BS3]
= 0,733·[CB].
Точка S4
находится в центре звена CD.
Дано:
ω1 = 10 с-1;
lOA = 0,19 м;
lCB = 0,15 м;
lCD = 0,22 м;
[OB] = 0,33 м;
H = 0,17 м.
Найти:
Скорости и ускорения точек А', С, D, S3, S4. . Определить угловые скорости и угловые ускорения звеньев СВА', CD.
Решение:
2.1. Определяем окружную скорость точки А, принадлежащей кривошипу.
![]() м/с.
м/с.
Строим план скоростей.
2.2. В произвольном месте ставим точку р – полюс скоростей. Из полюса проводим вектор скорости точки А произвольной длины и направлением перпендикулярным звену ОА, как показано на рис.16.
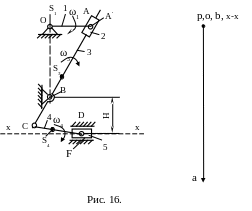
. Определяем масштаб плана скоростей
![]() м·с-1/мм,
м·с-1/мм,
где [pa] – длина вектора скорости точки А, мм.
2.4. Определяем скорость точки А', принадлежащей кулисе. Её скорость может быть представлена как векторная сумма скоростей: переносной скорости VA и относительной скорости точки А' относительно А – VА'A. C другой стороны, если точка А' принадлежит кулисе, то имеет окружную скорость относительно неподвижной точки В – VA'B и плюс переносная скорость точки В – VB. Точка В неподвижна, значит VB = 0. Таким образом, можем получить систему векторных уравнений:
![]()
Решаем её графически.
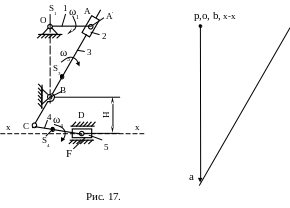
2.5. Вектор скорости VA у нас уже есть. Линия скорости VА'A проходит параллельно кулисе СВА'. Проводим её через конец вектора (рис. 17).
2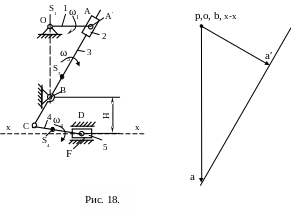 .6.
Решаем второе уравнение системы.
Поскольку вектор скорости VB
= 0 , значит
построение вектора скорости VА'B
начинаем из полюса p.
Вектор скорости VА'В
направлен перпендикулярно кулисе СВА'.
Проводим его до пересечения с линией
действия скорости VА'A,
как показано на рис.18.
.6.
Решаем второе уравнение системы.
Поскольку вектор скорости VB
= 0 , значит
построение вектора скорости VА'B
начинаем из полюса p.
Вектор скорости VА'В
направлен перпендикулярно кулисе СВА'.
Проводим его до пересечения с линией
действия скорости VА'A,
как показано на рис.18.
Полученный
векторный треугольник есть план скоростей
для ведущего механизма I(0,1)
и присоединённой к нему структурной
группы II
класса 3 вида 2 порядка – II(2,3).
Вектор
![]() показывает величину
и направление скорости точки A'
– VA'.
Вектор
показывает величину
и направление скорости точки A'
– VA'.
Вектор
![]() показывает скорость
точки A'
относительно А. Вектор
показывает скорость
точки A'
относительно А. Вектор
![]() показывает скорость
точки А относительно А'.
показывает скорость
точки А относительно А'.
2.7. Точка С, также как и точка А', принадлежит кулисе, но её окружная скорость VC направлена в обратную сторону скорости точки А' и определяется из отношений:
![]() мм.
мм.
Откладываем
из полюса р вектор
![]() (рис. 19). Положение точки S3
на плане скоростей определяется отрезком
[bs3].
Длину отрезка [bs3]
найдём из соотношения:
(рис. 19). Положение точки S3
на плане скоростей определяется отрезком
[bs3].
Длину отрезка [bs3]
найдём из соотношения:
![]() мм.
мм.
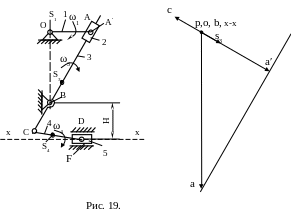
2.8. Следующая структурная группа относится к II классу 2 вида 2 порядка – II(4,5).
Скорость точки D определим так же, решая графически систему векторных уравнений.
![]()
2.8.1. Решаем первое уравнение. Через конец вектора проводим перпендикулярно шатуну CD линию действия скорости VDC (рис. 20).
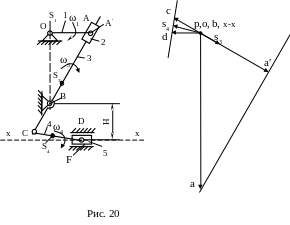
2.8.2.
Решаем второе векторное уравнение.
Скорость Vx-x
= 0, поэтому построение вектора скорости
VDx-x
начинаем из полюса p.
Проводим
параллельно направляющей x-x
до пересечения с линией действия скорости
VDC.
Вектор
![]() показывает скорость
точки C
относительно точки D.
Вектор
показывает скорость
точки C
относительно точки D.
Вектор
![]() показывает скорость точки D
относительно точки С.
показывает скорость точки D
относительно точки С.
2.9. Множество векторов, проведённых из полюса p на линию cd, покажут абсолютные скорости точек, принадлежащих звену CD. Если точка S4 находится в середине звена CD, то вектор, проведённый из полюса p на середину [cd] покажет скорость VS4. Точка S4 может находиться в любом месте на звене CD, тогда её положение на плане скоростей (рис. 20) будет определено отрезком [ds4]. Длину отрезка [ds4] найдём из соотношения:
![]() мм.
мм.
2.10. Определяем численные значения скоростей VA'A, VS3, VC, VS4, VDC, VD.
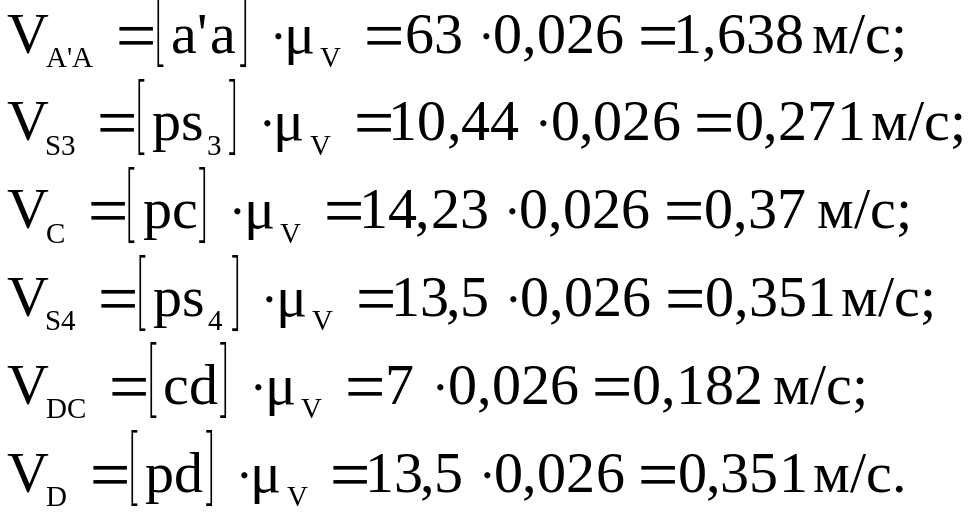
2.11. Находим угловые скорости звеньев CBA', CD.
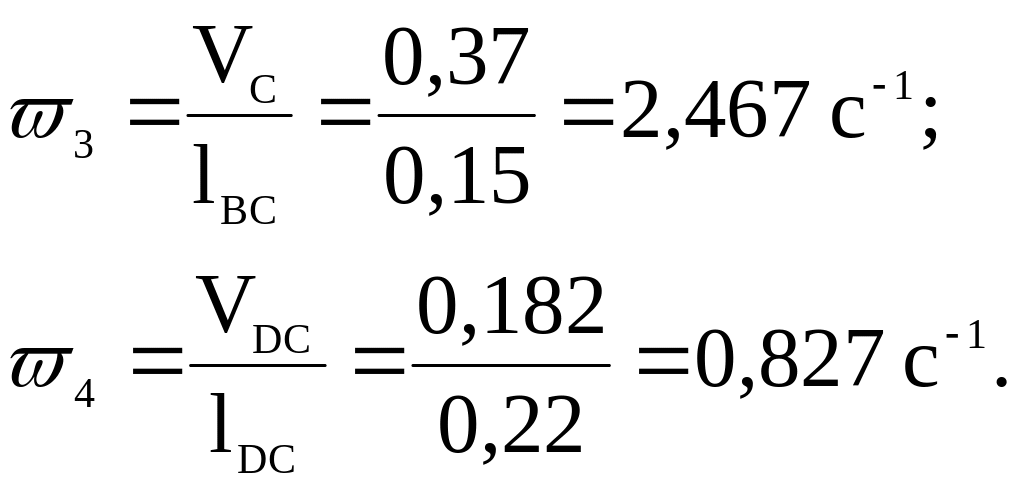
Строим план ускорений.
2.12. Построение плана ускорений начинаем, также как и построение плана скоростей, с ведущего звена ОА. Кривошип ОА вращается с постоянной угловой скоростью, поэтому его угловое ускорение ε1 = 0, но есть центробежное ускорение
![]() м/с2.
м/с2.
2.13.
В произвольном месте ставим точку π –
полюс ускорений. Из полюса проводим
вектор центробежного (нормального)
ускорения точки А произвольной длины
![]() .
Его направление параллельно звену ОА
(рис.21). Масштаб ускорений:
.
Его направление параллельно звену ОА
(рис.21). Масштаб ускорений:
![]() .
.
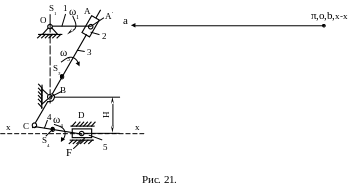
2.14.
Ускорение точки А', принадлежащей кулисе
3, будет состоять из переносного ускорения
точки А, кориолисова ускорения
![]() и релятивного ускорения
и релятивного ускорения
![]() .
Ускорение точки А' можно также получить
сложением ускорений aB
= 0, нормального ускорения
.
Ускорение точки А' можно также получить
сложением ускорений aB
= 0, нормального ускорения
![]() и тангенциального ускорения
и тангенциального ускорения
![]() .
Получаем векторную систему уравнений.
.
Получаем векторную систему уравнений.
![]()
2.15.
Величина ускорения
![]() определяется по формуле
определяется по формуле
![]() м/с2.
м/с2.
2.16.
Величина ускорения
![]() определяется по
формуле
определяется по
формуле
![]() м/с2.
м/с2.
2.17. Решаем графически векторную систему уравнений.
2.17.1.
Ускорение aA
у нас уже изображено вектором
.
Через конец вектора
проводим вектор
![]() .
Направление вектора
определяется поворотом вектора
относительной скорости
.
Направление вектора
определяется поворотом вектора
относительной скорости
![]() в сторону вращения кулисы на 90○
(рис. 22).
в сторону вращения кулисы на 90○
(рис. 22).
Масштабная длина вектора ускорения определяется по формуле
![]() мм.
мм.
2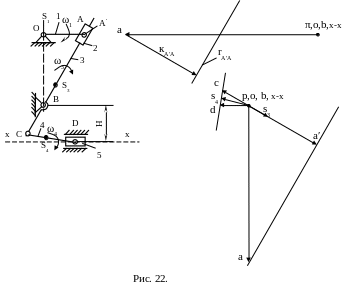 .17.2.
Через конец вектора кориолисова ускорения
проводим линию действия релятивного
ускорения
параллельно
звену СВА' (рис. 22).
.17.2.
Через конец вектора кориолисова ускорения
проводим линию действия релятивного
ускорения
параллельно
звену СВА' (рис. 22).
2.17.3.
Решаем второе векторное уравнение.
Поскольку ускорение точки В равно 0, то
построение начинаем из полюса π. Вектор
![]() направлен параллельно СBA'
от А' к В. Длина вектора
в принятом масштабе
направлен параллельно СBA'
от А' к В. Длина вектора
в принятом масштабе
![]() мм.
мм.
2.17.4.
Через конец [nA'B]
проводим вектор ускорения
![]() по направлению перпендикулярному звену
СВА' до пересечения с линией действия
релятивного ускорения
по направлению перпендикулярному звену
СВА' до пересечения с линией действия
релятивного ускорения
![]() .
Из полюса в точку пересечения проводим
вектор ускорения aA'
–
.
Из полюса в точку пересечения проводим
вектор ускорения aA'
–
![]() (рис. 23). В масштабе
вектор
показывает величину
и направление полного ускорения точки
А'.
(рис. 23). В масштабе
вектор
показывает величину
и направление полного ускорения точки
А'.
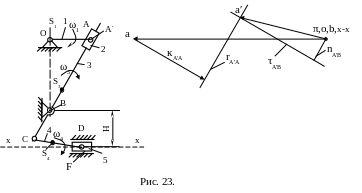
2.18.
Вектор ускорения точки С –
![]() определим из соотношения
определим из соотношения
![]() мм.
мм.
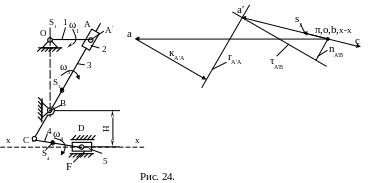
2.19. Точка s3 сохраняет своё подобие на плане ускорений также как и на плане скоростей (рис.24).
![]()
 мм.
мм.
2.20. Следующая структурная группа состоит из звеньев 4-5. Для определения ускорений этой группы имеем систему уравнений
![]()
Так
как ось x-x
направляющей неподвижна, то ускорение
и кориолисово
ускорение
![]() равны 0. Тогда система уравнений примет
вид
равны 0. Тогда система уравнений примет
вид
![]()
2.21.
Определяем нормальное ускорение
![]() .
.
![]() м/с2.
м/с2.
2.22. Решаем графически векторную систему уравнений.
2.22.1.
Длина вектора ускорения
![]() в
принятом масштабе
в
принятом масштабе
![]() мм.
мм.
2.22.2.
Через конец вектора
проводим параллельно звену CD
вектор
![]() по направлению от D
к С. Через конец вектора
проводим линию действия ускорения
по направлению от D
к С. Через конец вектора
проводим линию действия ускорения
![]() перпендикулярно звену СD.
перпендикулярно звену СD.
2.22.3. Из второго уравнения имеем условие, при котором ускорение точки D равно релятивному ускорению D относительно неподвижной направляющей вдоль оси х-х. Проводим из полюса вектор до пересечения с линией действия ускорения (рис.25).
2.23. Множество векторов, проведённых из полюса π на линию сd, покажут полные ускорения точек, принадлежащих звену CD. Если точка S4 расположена в середине звена CD, то вектор, проведённый из полюса π на середину [ed] – вектор , покажет полное её ускорение (рис.25). На рис.26 показан фрагмент плана ускорений в масштабе μ'a.
![]() м·с-2/мм.
м·с-2/мм.
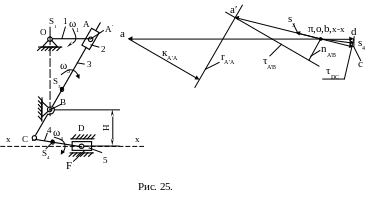

2.24. Из полученного плана ускорений определяем значения ускорений точек А', С, D, S3, S4.

2.25. Определяем значения тангенциальных ускорений.
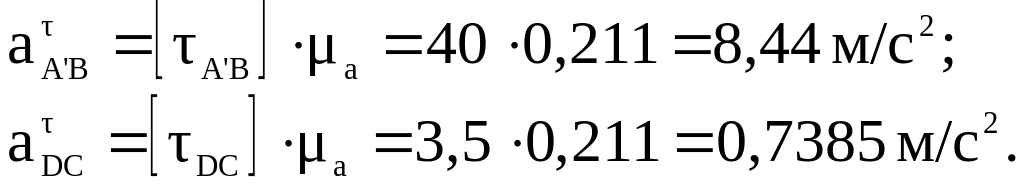
2.26. Определяем угловые ускорения звеньев СBA', CD.
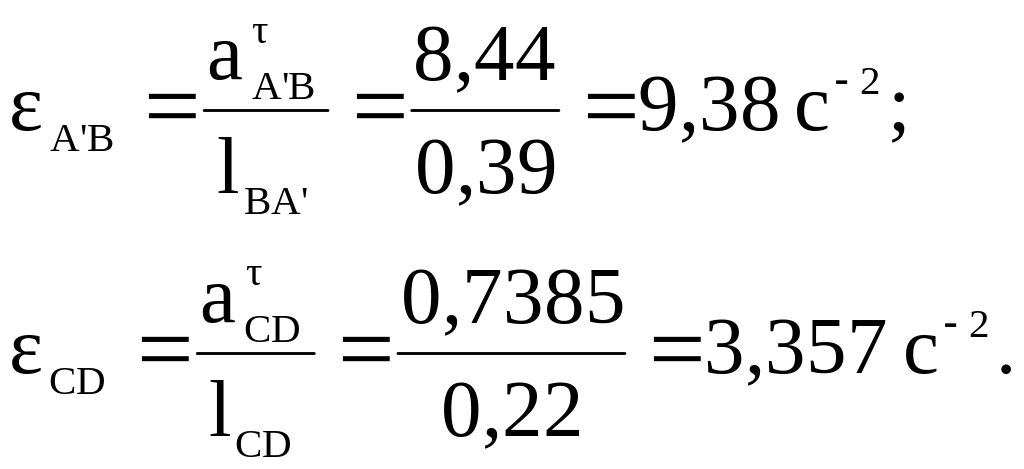
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1.Сапрыкин В.Н. Техническая механика.- М.: Издательство Эксмо, 2005.-560с.
2. Сурин В.М. Прикладная механика: учеб. пособие/В.М. Сурин. – Мн.: Новое знание, 2005. – 338с.
3. Программный пакет AРM WinMachine.
Содержание
Введение………………………………………………………………………………..3
Принятые условные обозначения и их прочтение…………………………...4
Кинематический анализ механизмов……………………………………...5
Пример 1………………………………………………………………………………..9
Пример 2……………………………………………………………………………....24
Рекомендуемая литература…………………………………………………….....36
Содержание…………………………………………………………………………..37
