m35674_6

Тема 5.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, ИХ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

Основные понятия

Случайной называют величину, которая в результате испытания принимает одно и только одно из своих возможных значений, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайные величины подразделяются на два класса  дискретные и непрерывные.

Случайная величина называется дискретной, если все ее возможные значения можно изобразить изолированными точками числовой прямой.

Примеры дискретных случайных величин:

1. количество очков, выпавших на верхней грани игрального кубика при его однократном подбрасывании;

2. количество опечаток на странице рукописи;

3. число претендентов на вакантную должность;

4. число зерен в колоске злака.

Случайная величина называется непрерывной, если все ее возможные значения сплошь заполняют некоторый промежуток числовой прямой.

Примеры непрерывных случайных величин:

1. процент жира в молоке;

2. количество осадков, выпадающих в некоторой местности за некоторый месяц;

3. время ожидания автобуса на остановке.

Случайные величины принято обозначать прописными буквами конца латинского алфавита: а их возможные значения  соответственными строчными буквами с числовыми индексами. Так, например, возможные значения случайной величины .

Запись означает вероятность того, что случайная величина приняла значение . Коротко эту вероятность обозначают через : .

Аналогично  вероятность того, что случайная величина приняла значение и т.д.

Соответствие между всеми возможными значениями случайной величины и их вероятностями называют законом распределения случайной величины (распределением вероятностей случайной величины). Для дискретной случайной величины закон распределения задается в виде таблицы

				…
				…		,

где .

Это способ задания дискретной случайной величины часто называют рядом распределения. Ряд распределения дискретной случайной величины может быть представлен геометрически в виде многоугольника распределения (рис. 5.1).

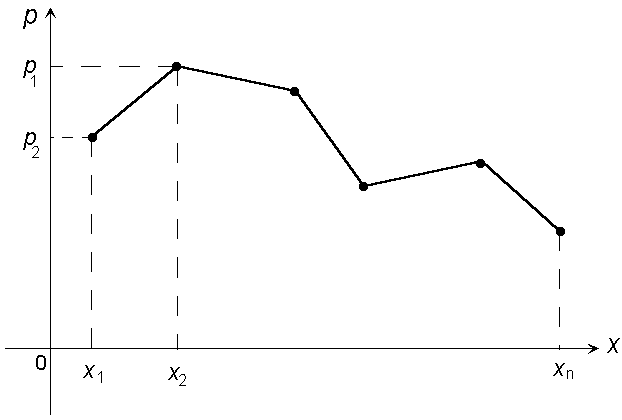
Рис. 5.1. Многоугольник распределения.

Пример 5.1. Пусть число выпадений герба при бросании двух монет. Составить закон распределения случайной величины .

Решение. Случайная величина может принимать, очевидно, значения 0, 1, 2. Обозначим соответствующие им вероятности через и рассмотрим события

{обе цифры, т.е. герб не выпал ни разу};

{герб-цифра или цифра-герб, т.е. герб выпал один раз};

{оба герба, т.е. герб выпал два раза}.

Тогда

Таким образом, получаем искомый закон распределения:

		0	1	2
		1/4	1/2	1/4	.

Очевидно, .

Пример 5.2. Стрелок, имея 4 патрона, стреляет до первого попадания в цель. Вероятность попадания при каждом выстреле постоянна и равна 0,6. Построить закон распределения числа использованных патронов.

Решение. Заметим, что стрелок использует -й патрон, если -й и все предыдущие выстрелы закончились промахами.

Введем в рассмотрение случайную величину число использованных патронов  и случайные события

{попадание в цель при первом выстреле};

{промах при первом выстреле и попадание при втором};

{промахи при двух первых выстрелах и попадание при третьем};

{промах при первых трех выстрелах}.

Очевидно, вероятность промаха при одном выстреле равна 10,6=0,4. Применяя теорему умножения вероятностей для независимых событий, получаем

Отсюда следует, что искомый закон распределения случайной величины имеет вид

		1	2	3	4
		0,6	0,24	0,096	0,064	.

Заметим еще раз, что сумма вероятностей в нижней строке таблицы равна единице.

Математическим ожиданием (средним ожидаемым значением) дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности:

Разность называется отклонением случайной величины от ее математического ожидания.

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Для вычисления дисперсии дискретной случайной величины можно пользоваться одной из двух формул:

где , или так называемой универсальной формулой

то есть

Наряду с математическим ожиданием, дисперсия является важнейшей числовой характеристикой случайной величины. Она характеризует разброс, рассеяние значений случайной величины относительно ее математического ожидания. Однако дисперсия имеет одно не совсем удобное качество: ее размерность равна размерности квадрата случайной величины. Поэтому в качестве показателя рассеяния значений случайной величины относительно ее математического ожидания рассматривают чаще среднее квадратическое отклонение случайной величины (с.к.о.):

Эта величина имеет ту же размерность, что и случайная величина .

Пример 5.3. Заданы законы распределения двух независимых случайных величин :

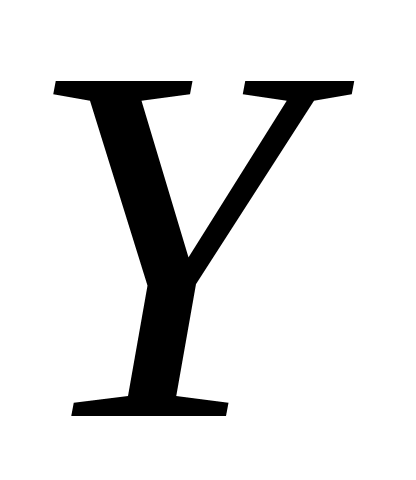
	-4	2	6	8			1	3
	0,2	0,1	0,3	0,4			0,2	0,8

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 3X  5Y.

Решение.

1. Найдем математические ожидания случайных величин :

,

2. Напишем законы распределения случайных величин :

	16	4	36	64			1	9
	0,2	0,1	0,3	0,4			0,2	0,8

3. Найдем математические ожидания случайных величин и :

;

.

4. Найдем дисперсии случайных величин и с помощью универсальной формулы:

;

5. Пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин и , окончательно получим

;

6. Найдем среднее квадратическое отклонение случайной величины Z:

Для непрерывных случайных величин закон распределения вероятностей, очевидно, не может быть задан в виде таблицы подобно тому, как это было сделано для дискретной случайной величины, так как нельзя перечислить все ее возможные значения в силу их структурных особенностей (кроме того, вероятность каждого отдельного значения непрерывной случайной величины равна нулю).

Представление о распределении вероятностей непрерывной случайной величины получают с помощью функции распределения либо плотности распределения вероятностей.

Функцией распределения вероятностей (интегральным законом распределения) непрерывной случайной величины называется непрерывная функция , определяемая равенством

Отметим, что

1. неубывающая функция и принимает значения от 0 до 1, когда пробегает значения от ;

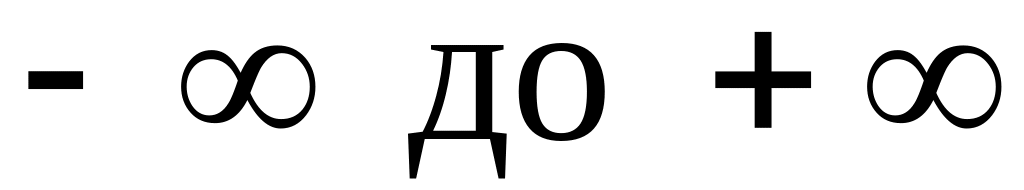2. вероятность того, что принимает значения между и 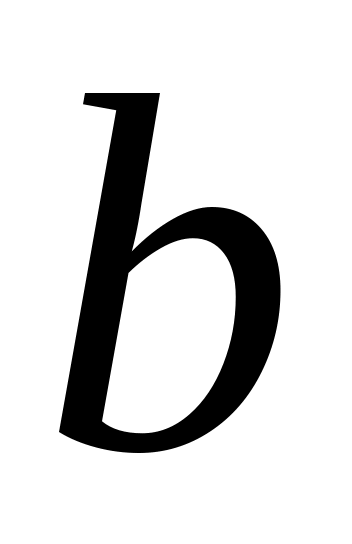вычисляется по формуле

Пример графика функции распределения вероятностей непрерывной случайной величины изображен на рис. 5.2.

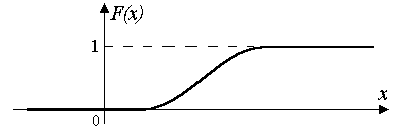
Рис. 5.2. Пример графика функции распределения вероятностей

непрерывной случайной величины.

З а м е ч а н и е. Функция распределения используется и как закон распределения дискретной случайной величины, представляя собой графически уже разрывную ступенчатую линию.

Пример 5.4. Два стрелка делают по одному выстрелу. Вероятности попадания в мишень соответственно равны 0,5, 0,4. Составить закон распределения числа попаданий в цель, начертить многоугольник распределения и график функции распределения.

Решение.

1. Получим ряд распределения случайной величины X. Пусть

А = {первый стрелок попал в цель};

В = {второй стрелок попал в цель};

Х – число попаданий в цель.

Вычислим вероятности того, что Х примет значения 0, 1 и 2:

;

;

Таким образом, ряд распределения случайной величины X имеет вид:

Х	0	1	2
Р	0,3	0,5	0,2

2. Строим многоугольник распределения (рис. 5.3):

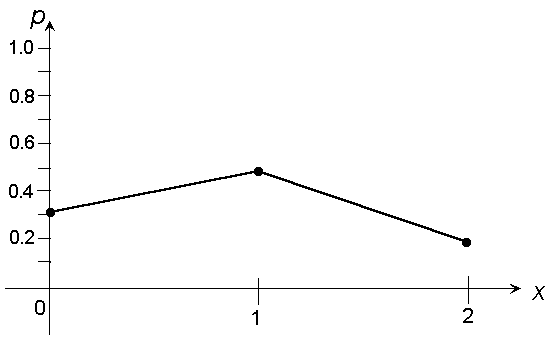
Рис. 5.3. Многоугольник распределения.

3. Строим аналитически функцию распределения случайной величины X.

1)

2)

3) либо

4)

Итак,

4. Строим график (рис. 5.4).

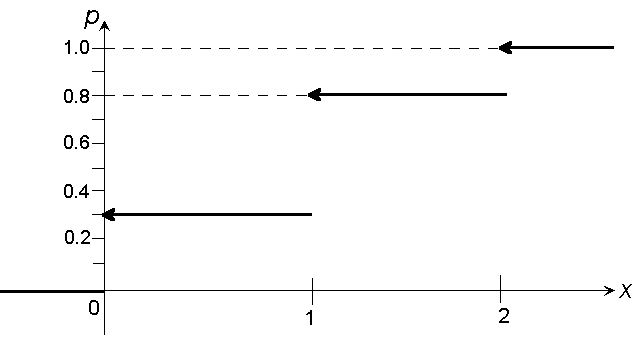
Рис. 5.4. График функции распределения .

Плотностью распределения вероятностей (дифференциальным законом распределения) непрерывной случайной величины называется функция , определенная равенством

Выделим следующие свойства:

1)

2. 

3. 

4. 

З а м е ч а н и я.

1. График дифференциальной функции f(x) принято называть кривой распределения.

2. Если задана кривая распределения, то по ней можно узнать, чему равна вероятность P(α < X< β). Действительно, из свойства 4) следует, что P(α < X< β) равна площади криволинейной трапеции, ограниченной кривой распределения, осью абсцисс и прямыми x = α и x = β (рис. 5.5). Свойство 2) говорит о том, что площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

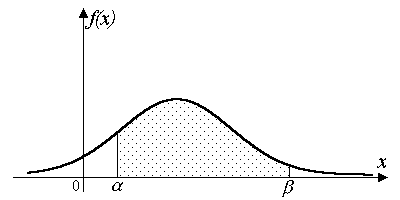
Рис. 5.5. Геометрический смысл P(α < X< β).

3. Объект называется дифференциалом или элементом вероятности и имеет следующий геометрический смысл (рис. 5.6).

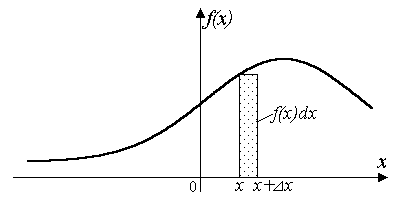
Рис. 5.6. Геометрический смысл элемента вероятности .

Пример 5.5. Продолжительность жизни растений некоторого вида в определенной среде представляет собой непрерывную случайную величину . Пусть плотность распределения вероятностей имеет вид

.

1. Какова функция распределения случайной величины ?

2. Какая доля растений данного вида умирает за период в 100 дней?

3. Если некоторое растение живет в течение 100 дней, то какова вероятность того, что оно проживет еще не менее 100 дней?

Решение.

1. Функция распределения вероятностей для будет выглядеть следующим образом:

2. Доля растений, которые умирают за период в 100 дней, выражается вероятностью

3. Искомая в этом пункте вероятность составляет

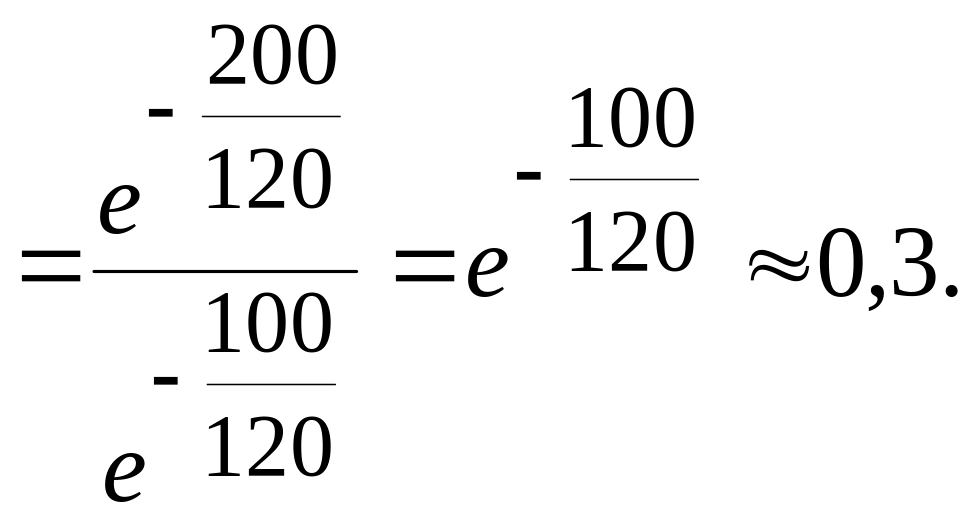
Таким образом, примерно 30% тех растений, которые не умирают за 100 дней, будут жить по крайней мере и следующие 100 дней.

Пример 5.6. Случайная величина x задана функцией распределения

Найти плотность вероятности f(x), построить графики функций F(x) и f(x) и вычислить P(1 x  2).

Решение.

1. Так как , то

2. Строим графики функций F(x) и f(x) (рис. 5.7).

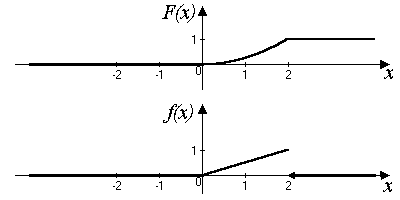
Рис. 5.7.

3. Вычисляем искомую вероятность P(1 X  2).

Непрерывные случайные величины, как и дискретные, имеют числовые характеристики которые вычисляются по следующим формулам:

или

Пример 5.7. Непрерывная случайная величина Х имеет закон распределения

Найти значение параметра А, функцию распределения вероятностей случайной величины Х, числовые характеристики М(Х), , (Х) и Р(0  Х  2).

Решение.

1. Для отыскания значения А воспользуемся свойством дифференциальной функции (х)

Получаем

то есть

2. Функцию распределения ищем по формуле

.

1)

2)

3) .

3. Учитывая, что 0 х  5, вычислим М(Х):

Для нахождения дисперсии D(Х) воспользуемся универсальной формулой:

Среднее квадратическое отклонение будет равно

(Х) = = .

4. Теперь воспользуемся формулой

и вычислим Р(0 X  2):