Тема 4. Проверка случайной величины на

Нормальное распределение по критерию пирсона (χ2- хи-квадрат)

Выяснение вопроса о принадлежности выборочных данных нормально распределенному признаку генеральной совокупности является одной из важных задач математической статистики. Предположение о нормальном распределении некоторой случайной величины требуется, например, в основных положениях дисперсионного и корреля­ционно-регрессионного анализа.

Существует несколько способов, позволяющих по выбороч­ным данным с различной степенью уверенности принять или от­вергнуть предположение о нормальном распределении признака. Один из них рассматривается ниже.

Пусть непрерывная случайная величина (признак) Х пред­ставлена выборкой значений в виде интервального распределения, причем известны выборочное среднее и исправленное выбороч­ное среднее квадратическое отклонение S .

Пусть имеются основания предполагать, что Х подчинена нормальному закону распределения (например, из визуального со­ответствия гистограммы и нормальной кривой).

Проверка этого предположения на уровне значимости α с помощью критерия Пирсона осуществляется по следующей схеме.

1) Нужно проанализировать интервальное распределение вы­борки, объем которой , и в случае, если какому-нибудь частичному интервалу выборочных значений соответствует эмпири­ческая частота m_i, которая меньше, чем 5, этот интервал следует объединить с соседним (соседними), поставив новому интервалу в соответствие сумму эмпирических частот объединенных интерва­лов. Так как нормальное распределение определено для всех дей­ствительных значений х, то принято левую границу первого час­тичного интервала расширить до — , а правую границу по­следнего — до + . По окончании описанной процедуры будем обозначать число частичных интервалов через k .

2) В предположении, что исследуемая случайная величина Х действительно нормально распределена с параметрами и S

(X~N( ,S)), нужно вычислить вероятности попадания ее значений в каждый из m частичных интервалов по формуле

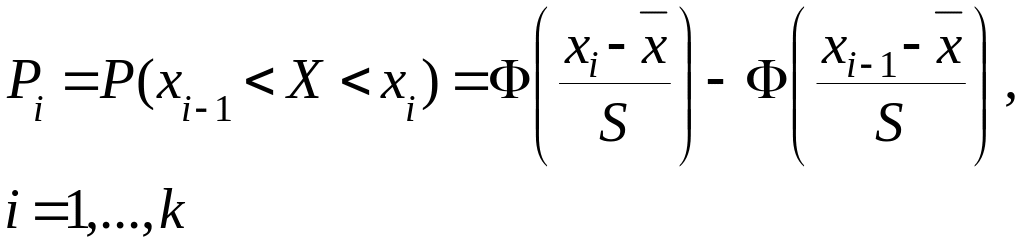(1)

где х_i-1, х_i - концы частичных интервалов, причем x₀ и x_k за­менены соответственно на — и + . При безошибочном счете должно выполняться условие

3) Нужно вычислить теоретические частоты m_i^Т по формуле

т_i^T=пР_i , (2)

где n - объем выборки. Отметим, что при этом должно выполнять-

ся условие

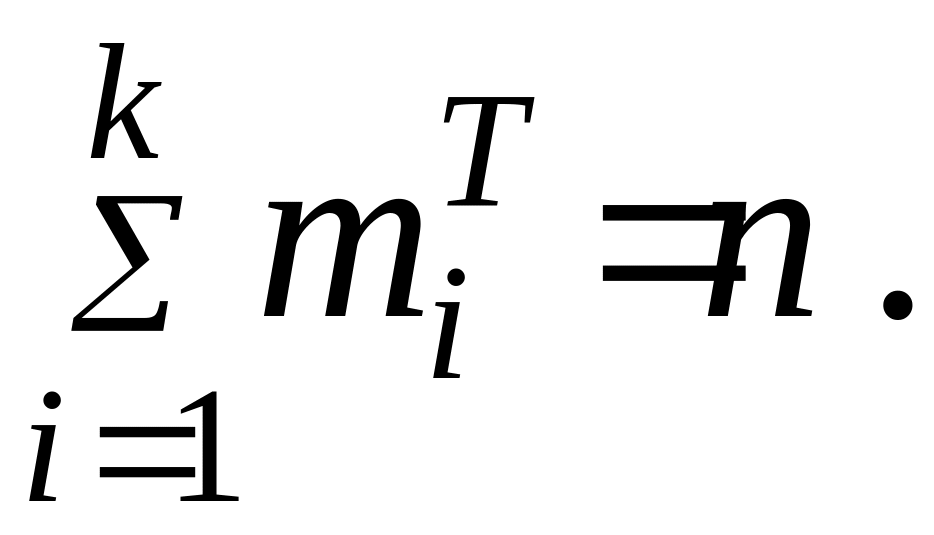
4) Теперь требуется вычислить наблюдаемое значение крите­рия χ² :

(3)

Кроме того, нужно найти критическое значение критерия χ² (χ²_kp.) в зависимости от выбранного уровня значимости α и числа степеней свободы ν = k - 3 . Это осуществляется с помощью таблицы Приложения 2.

5) Наконец, необходимо сравнить полученные значения χ² и χ²_kp:

если χ² > χ²_kp , то гипотеза о нормальном распределении

случайной величины Х на уровне значимости а отвергается;

если χ² < χ²_kp., то считают, что на заданном уровне значи­мости а нет оснований отвергнуть гипотезу о нормальном распре­делении рассматриваемой случайной величины Х .

ПРИМЕР

Проведем статистический анализ результатов мно­гократного (n=135) определения титра инфекционности вируса эталонной серии вакцины против ньюкаслской болезни птиц на близость распределения экспериментальных данных, полученных в течение 38 месяцев, к нормальному.

Пусть выборочные данные представлены следующим распре­делением:

Таблица 4.1

Интервалы значений (igЭИД50/мл)	7,85-8,05	8,05-8,25	8,25-8,45	8,45-8,65	8,65-8,85
Частоты значе­ний	1	2	3	10	28

продолжение

8,85-9,05	9,05-9,25	9,25-9,45	9,45-9,65	9,65-9,85	9,85-10,05
30	29	14	13	3	2

Пусть при этом вычислены = 9 и S = 0,4.

Согласно рекомендациям, данным выше, объединим первые три частичные интервала таблицы 1 и последние два интервала. В результате получим уже 8 (k = 8) частичных интервалов (вместо первоначальных одиннадцати). Теперь сформируем и заполним по формулам (1) - (3) следующую таблицу.

Таблица 4.2

Интервалы значений
- 8,45	0,0838	6	11,31	2,49
8,45 - 8,65	0,1056	10	14,26	1,27
8,65 - 8,85	0,1663	28	22,45	1,37
8,85 - 9,05	0,1921	30	25,93	0,64
9,05 - 9,25	0,1879	29	25,37	0,52
9,25 - 9,45	0,1351	14	18,24	0,99
9,45 - 9,65	0,0776	13	10,48	0,61
9,65 -	0,0516	5	6,96	0,55
Сумма	1	135	135	8,44

Здесь

……………………………………………………………………………

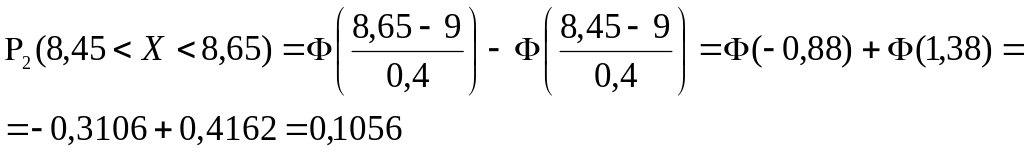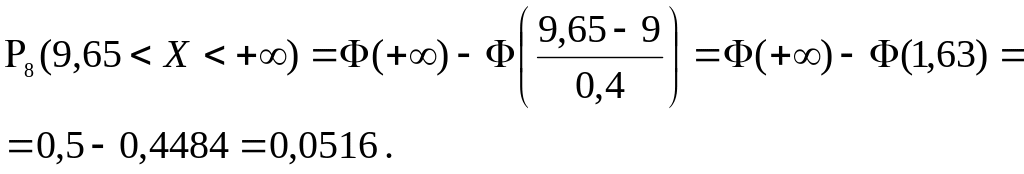
Поскольку

χ²_kp (0,05; 8-3)= χ²_kp (0,05; 5)=11,1,

то χ² < χ²_kp,

и на уровне значимости α=0,05 нет оснований отвергнуть предположение о нормальном распределении титра инфекционности вируса эталонной серии вакцины против ньюкаслской болезни птиц.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Что называется нормально распределенной случайной ве­личиной?

2. Как вычисляется вероятность попадания значений нор­мальной случайной величины в заданный интервал?

3 Какими свойствами обладает функция Лапласа?

4. Какой должна быть структура выборки и каким требова­ниям она должна удовлетворять при проверке предположения о нормаль­ном распределении признака с помощью критерия Пирсона?

5. Как искать и S для интервального распределения вы­борки?

6. Как вычисляются теоретические частоты выборочных зна­чений признака для интервального распределения выборки?

7. Как записывается формула для нахождения наблюдаемого значения критерия Пирсона?

8. От каких параметров зависит величина χ²_kp ?

9. Сформулируйте правило для проверки при заданном уров­не значимости a предположения о нормальном распределении признака Х с помощью критерия Пирсона, если известны наблюдаемое χ² и критическое χ²_kр значения критерия.