
4536
.pdf21
Одинаковые значения величины Z объединяем, складывая их вероятности. Закон распределения случайной величины Z будет иметь вид:
Z=X+Y |
|
1 |
|
3 |
|
4 |
|
5 |
|
6 |
|
|
7 |
P |
0,02 |
|
0,1 |
|
0,16 |
|
0,12 |
|
0,36 |
|
0,24 |
||
M(Z) = 1 · 0,02 |
+ 3 ·0,1 + 4 · 0,16 |
+ 5 · 0,12 |
+ 6 · 0,36 |
+ 7 |
· 0,24 |
= 5,24 |
|||||||
Или М(Z) = M(X) + M(Y), где |
|
|
|
|
|
|
|
|
|||||
M(X) = 1 · 0,1 |
+ 3 · 0,3 |
+ 4 · 0,6 = 3,4 |
|
|
|
|
|
|
|||||
M(Y) = 0 · 0,2 |
+ 2 · 0,4 |
+ 3 · 0,4 = 2 |
|
|
|
|
|
|
|||||
Тогда M(Z) = 3,4 + 2 = 5,4
Вычислим дисперсию случайной величины Z по формуле :
D(Z) = M(Z2) – [ M(Z)]2, где
M(Z2) = 1 · 0,02+9 · 0,1+16 · 0,16 +25 · 0,12+36 · 0,36+43 · 0,24 = 31,2. Тогда D(Z) = 31,2 – (5,4)2 = 2,04.
Или D(Z) = D(X) + D(Y), где
D(X) = 1 ∙ 0,1 + 9 ∙ 0,3 + 16 ∙ 0,6 – (3,4)2 = 0,84 D(Y) = 0,2 ∙ + 4 ∙ 0,4 + 9 ∙ 0,4 – (2)2 = 1,2
Таким образом D(Z) = 0,84 + 1,2 = 2,04.
в) Составим закон распределения V = X ·Y.
Произведением случайных величин X и Y называется случайная величина V = X · Y , возможные значения которой равны произведениям каждого возможного значения X на каждое возможное значение Y . Если X и Y независимы, то вероятности возможных значений V = X · Y равны произведениям вероятностей сомножителей.
V=X∙Y |
|
1·0=0 |
|
1·2=2 |
|
1·3=3 |
3·0=0 |
|
3·2=6 |
|
3·3=9 |
4·0=0 |
|
4·2=8 |
4·3=12 |
||||||||
P |
|
0,02 |
|
0,04 |
|
0,04 |
|
0,06 |
|
|
0,12 |
|
0,12 |
0,12 |
|
0,24 |
0,24 |
|
|
||||
Одинаковые значения величины V = X · Y |
объединяем, |
складывая |
их |
||||||||||||||||||||
вероятности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Закон распределения V = X ·Y записываем так: |
|
|
|
|
|
|
|
|
|||||||||||||||
V=X ∙Y |
|
|
|
2 |
|
|
|
|
3 |
|
|
6 |
|
8 |
|
9 |
|
|
12 |
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
P |
|
0,2 |
|
|
0,04 |
|
0,04 |
|
|
0,12 |
|
0,24 |
|
0,12 |
|
0,24 |
|
|
|||||
Найдем M(V) = 0 · 0,2 |
+ |
2 · 0,04 |
+ 3 · 0,04 + |
6 · 0,12 |
+ 8 · 0,24 + |
9 |
|||||||||||||||||
· 0,12 + |
|
12 · 0,24 |
= 6,8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Или М(V) = M(X) ∙ |
M(Y) = 3,4 ∙ 2 = 6,8. |
|
|
|
|
|
|
|
|
|
|||||||||||||

22
2. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Пример 1: Непрерывная случайная величина Х задана функцией
распределения:
|
0, |
x |
0 |
||
|
x2 |
||||
F (х) |
, 0 x 2 . |
||||
4 |
|
||||
|
|
x |
2 |
||
|
1, |
|
|||
Требуется:
а) найти функцию плотности распределения f(x);
б) найти математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение σ (Х);
в) построить графики функций f(x) и F(x); г) найти P(-1 < Х < 1).
Решение:
а) По определению функции плотности вероятности f(x) = F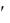 (x) , тогда
(x) , тогда
|
|
|
0, |
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
f (х) |
|
, |
0 |
x |
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) Для непрерывной случайной величины |
|
|
|
|
|||||||||||||||||||||
|
b x f (x) dx |
2 x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
М ( Х ) |
|
x dx |
|
|
|
|
x3 |
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||
0 2 |
|
|
|
|
6 |
|
|
|
3 |
|
|||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
b |
|
|
|
|
|
2 |
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
М ( Х 2 ) |
x 2 |
f (x) dx |
|
x 2 |
|
|
|
dx |
|
|
x 4 |
2 |
2 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
a |
|
0 |
|
|
2 |
|
|
|
|
|
|
8 |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D(X) = M(Х2) |
- [M (Х)]2 |
= |
2 - |
|
|
4 2 |
= |
2 |
. |
|
|
|
|
||||||||||||
|
|
3 |
|
9 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2
( Х ) D( Х ) 
 0,47.
0,47.
 9
9
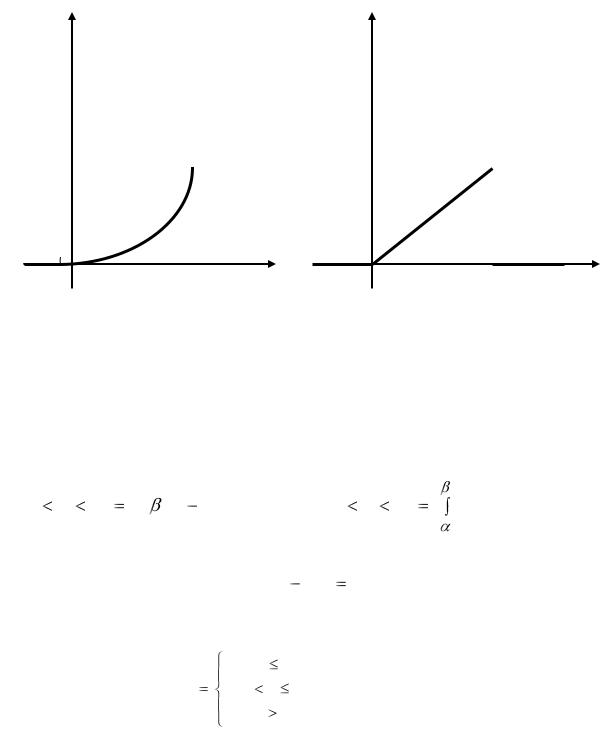
23
F(x)
f(x)
1 |
1 |
|
|
|
|
2 |
X |
2 |
X |
|
|
|
|
г) Для вычисления вероятности попадания непрерывной случайной величины в интервал (α ,β) можно применить одну из формул:
P ( α Х β) |
F( ) |
F(α ) |
|
или P ( α |
Х β) |
f(x) dx |
||
Применим первую формулу |
|
|
|
|
|
|
||
P (-1 < Х < 1) = |
F(1) - |
F(-1) = |
12 |
0 |
1 |
. |
|
|
|
4 |
4 |
|
|||||
|
|
|
|
|
|
|||
Пример 2. Случайная величина Х задана плотностью распределения:
|
0, |
x |
1 |
|
||
|
c |
|
|
|||
f (х) |
, 1 x |
5 |
. |
|||
8 |
||||||
|
|
x |
5 |
|
||
|
0, |
|
||||
|
|
|
|
|||
Требуется:
а) найти коэффициент С;
б) функцию распределения F(x);
Решение.
а) Плотность распределения f(x) должна удовлетворять условиям:

24
f (x) 0, |
f (x) dx |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
f (x) dx |
1 |
|
0 dx |
|
|
|
|
5 c |
dx |
0 dx |
|
|
c |
5 dx |
c |
x |
|
|||||
|
|
|
|
|
|
|
|
5 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||
|
|
|
|
|
|
1 8 |
|
8 |
8 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
|||||||
|
c |
|
(5 |
1) |
4 c |
|
|
|
1 |
|
C . |
|
|
|
|
|
|
|
|
|
||||
8 |
|
8 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как |
f (x) dx |
|
1 |
|
, следовательно, |
1 |
C 1, следовательно С = 2. |
|||||||||||||||||
|
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0, |
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
f (х) |
|
, 1 |
|
x |
5 |
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) Для нахождения функции распределения F(x) воспользуемся формулой
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) |
f (x) |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
Если |
х ≤ 1 , |
f(x) = 0, |
то |
|
F (x) |
|
|
0 dx |
|
|
0. |
||||||
Если 1 < х ≤ 5, |
|
1 |
|
|
x |
1 |
|
|
x |
|
|
х |
|
1 |
|
||
|
|
|
|
|
|
||||||||||||
F (x) |
0 dx |
|
|
dx |
|
(x 1) . |
|||||||||||
|
|
|
|
||||||||||||||
1 4 |
|
4 |
|
|
1 |
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если |
х > 1, |
|
1 |
|
|
5 1 |
|
х |
|
|
|
|
|
||||
F (x) |
0 dx |
|
|
|
|
dx |
|
0 dx |
1. |
|
|||||||
1 4 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||||
|
|
|
0, |
|
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
Итак , |
|
F ( X ) |
x 1 |
, 1 |
|
x |
5 . |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
||
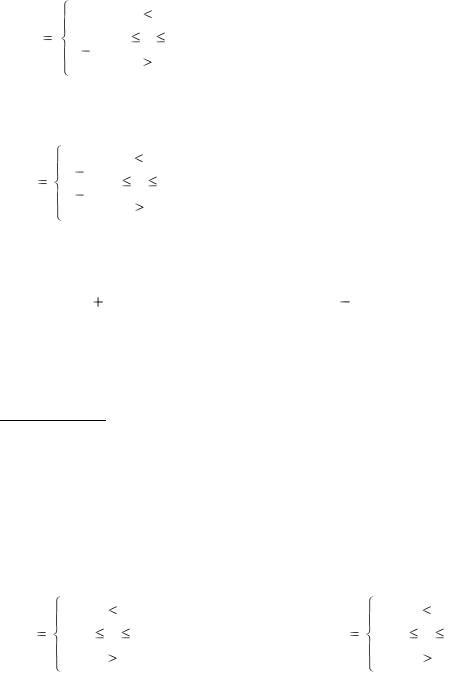
25
3. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Равномерное распределение
Непрерывная случайная величина Х распределена равномерно на отрезке [а, b], если на этом интервале ее функция плотности имеет вид
|
0, |
x |
a |
|
|
1 |
|||
f (x) |
, a x b . |
|||
|
||||
b a |
||||
|
0, |
x |
b |
|
|
|
|
||
Функция распределения для равномерного закона
|
0, |
x |
a |
|
|
x a |
|||
F (x) |
, a x b . |
|||
b a |
||||
|
x |
b |
||
|
1, |
|||
|
|
|
||
Математическое ожидание и дисперсия вычисляются по формулам
|
b |
a |
|
|
(b a) 2 |
|
М(Х) = |
|
|
; |
D(Х) = |
|
. |
|
2 |
12 |
||||
|
|
|
|
|
||
Пример 1. Поезда метро идут строго по расписанию. Интервал движения - 5 минут. Составить f(х) и F(х) случайной величины Х – времени ожидания очередного поезда и построить их графики. Найти М(Х), D(Х).
Решение: Случайная величина Х – время ожидания очередного поезда. Величина Х распределена равномерно на отрезке [0,5], поэтому
|
0, |
x |
0 |
|
0, |
x |
0 |
|||
|
1 |
|
|
x |
|
|||||
f (x) |
, 0 x 5 . |
F (x) |
, 0 x 5 |
|||||||
5 |
5 |
|||||||||
|
|
x |
5 |
|
|
x |
5 |
|||
|
0, |
|
1, |
|||||||
|
|
|
|
|
|
|||||
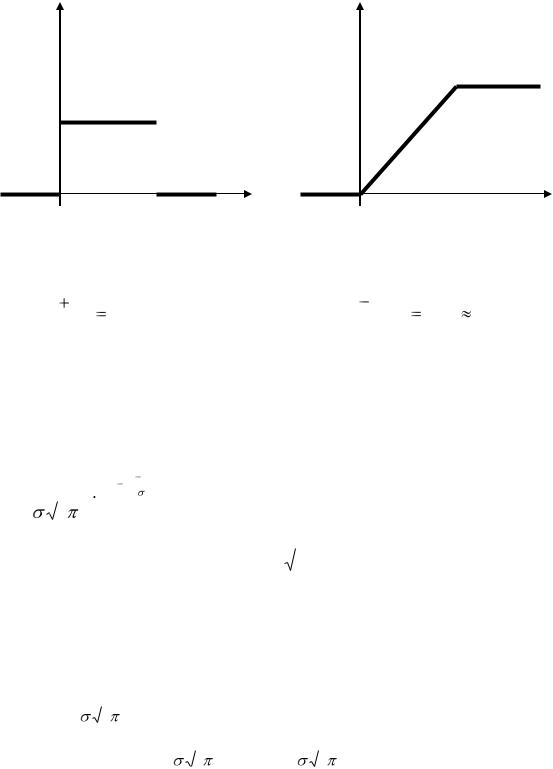
26
f(x) |
F(x) |
1
0,2
5 |
X |
5 |
X |
|
|
|
|
М(Х) = |
5 |
0 |
2,5 |
D(Х) = |
(5 |
0) 2 |
|
25 |
2,08. |
|
2 |
|
12 |
12 |
|||||
|
|
|
|
|
|
||||
2. Нормальное распределение
Закон нормального распределения должен быть изучен наиболее основательно, т.к. он часто применяется в теории и практике.
Непрерывная случайная величина Х распределена по нормальному закону, если ее плотность распределения вероятностей выражается формулой
|
|
1 |
|
|
|
( x a)2 |
|
|
|
|||
f(х) = |
|
|
e |
2 |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Параметры а |
и σ имеют следующий вероятностный смысл: |
|||||||||||
|
|
|
|
|
σ 2= D(Х), |
|
|
|
||||
а = М(Х), |
|
|
|
|
σ = D(x) . |
|||||||
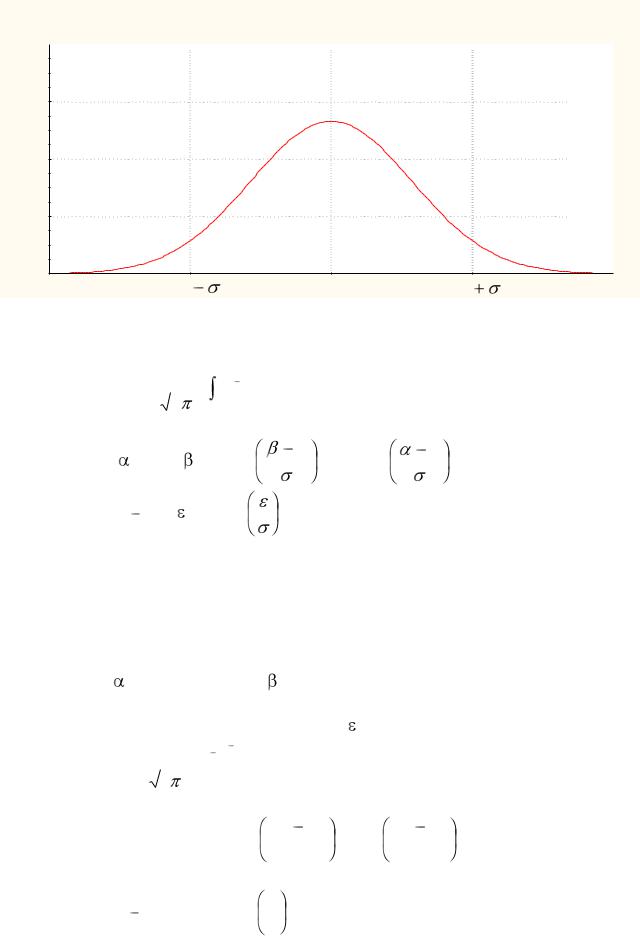
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
1.Функция ƒ(х) определена на всей оси Х.
2.При любых значениях Х функция принимает положительные значения, т.е. лежит выше оси ОХ.
3. |
Точка (а, |
1 |
|
) – точка max. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Точки перегиба (а-σ, |
1 |
|
) и (а+σ, |
1 |
|
). |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
2 e |
|
|
2 e |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Y
Probability Density Function27
|
|
y=normal(x;0;1) |
|
|
|
0,60 |
|
|
|
|
|
0,45 |
|
|
|
|
|
0,30 |
|
|
|
|
|
0,15 |
|
|
|
|
|
0,00 |
|
|
|
|
|
-3,50 |
-1,75 |
0,00 |
1,75 |
X |
3,50 |
|
a |
a |
a |
|
|
|
Если функция Лапласа задается формулой |
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
|
|
|
|
|
|
Ф(х) |
= |
|
|
|
|
e t |
/ 2 dt , то для нормально распределенной случайной |
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||
2 |
|
|
||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р ( |
< Х < ) = Ф |
|
|
|
a |
- Ф |
a |
. |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Р( |
Х |
а |
< |
) = 2Ф |
|
|
|
. |
|
|
|
|||||
|
|
|
|
|
||||||||||||
Пример 2. |
Детали, выпускаемые цехом, по размеру диаметра распределены |
|||||||||||||||
по нормальному закону. Стандартная длина диаметра детали равна а = 35,
среднее квадратическое отклонение |
σ = 4. Требуется: |
|||||||||||||||||||||
а) составить функцию плотности вероятностей; |
||||||||||||||||||||||
б) найти вероятность того, что диаметр наудачу взятой детали будет |
||||||||||||||||||||||
больше |
=34 |
|
и меньше |
= 40; |
|
|
|
|
|
|
||||||||||||
в) найти вероятность того, что диаметр детали отклонится от |
||||||||||||||||||||||
стандартной длины не более чем на |
= 2. |
|
|
|
||||||||||||||||||
|
|
|
1 |
|
|
|
( x |
35)2 |
|
|
|
|
|
|
|
|
|
|
|
|||
а) f(х) = |
|
|
е |
32 |
; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Р(34 < Х < 40 ) = |
Ф |
40 |
35 |
|
- Ф |
34 |
35 |
|
= Ф (1,25) + Ф (0,25) = = |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
4 |
|
|
4 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,3944 + 0,0987 = 0,4931; |
|
|
|
|
|
|
|
|
|
|||||||||||||
в) Р ( |
|
х |
|
35 |
|
< 2 ) = 2Ф |
2 |
|
= 2Ф (0,5) = 0,3829. |
|
||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
4 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
28
Контрольные задания, правила выполнения и оформления контрольной работы
Вариант для контрольного задания студент выбирает в соответствии с двумя последними цифрами своего учебного номера (шифра) по следующему правилу: вторая цифра номера варианта должна совпадать с последней цифрой шифра (учебного номера). Далее, если предпоследняя цифра четная, то первая цифра номера варианта должна быть равна 0 или 2; если же предпоследняя цифра нечетная, то первая цифра номера варианта должна быть равна 1. Например, при учебном номере 973076 студент решает вариант 16, при шифре 975046 решается вариант 06, при шифре 973045 – вариант 05, при шифре 973035 – вариант 15, при шифре 973030 – вариант 10, при шифре 973040 – вариант 20.
Номера |
Номера задач для контрольного задания |
||||
вариантов |
|
|
|
|
|
01 |
1 |
21 |
41 |
61 |
81 |
02 |
2 |
22 |
42 |
62 |
82 |
03 |
3 |
23 |
43 |
63 |
83 |
04 |
4 |
24 |
44 |
64 |
84 |
05 |
5 |
25 |
45 |
65 |
85 |
06 |
6 |
26 |
46 |
66 |
86 |
07 |
7 |
27 |
47 |
67 |
87 |
08 |
8 |
28 |
48 |
68 |
88 |
09 |
9 |
29 |
49 |
69 |
89 |
10 |
10 |
30 |
50 |
70 |
90 |
11 |
11 |
31 |
51 |
71 |
91 |
12 |
12 |
32 |
52 |
72 |
92 |
13 |
13 |
33 |
53 |
73 |
93 |
14 |
14 |
34 |
54 |
74 |
94 |
15 |
15 |
35 |
55 |
75 |
95 |
16 |
16 |
36 |
56 |
76 |
96 |
17 |
17 |
37 |
57 |
77 |
97 |
18 |
18 |
38 |
58 |
78 |
98 |
19 |
19 |
39 |
59 |
79 |
99 |
20 |
20 |
40 |
60 |
80 |
100 |
29
Задания
1.Магазин получает товар партиями по 100 штук. Если пять взятых наудачу образцов соответствуют стандартам, партия товара поступает на реализацию. В очередной партии 8 единиц товара с дефектом. Найти вероятность того, что товар поступит на реализацию.
2.Два бухгалтера обрабатывают равное количество счетов. Вероятность того, что первый бухгалтер допустит ошибку равна 0,005, для второго эта вероятность равна 0,01. При проверке счетов была найдена ошибка. Найти вероятность того, что ее допустил первый бухгалтер.
3.В ящике 20 деталей, 5 из них с дефектом. Наудачу извлекаются три детали.
Найти вероятность того, что среди извлеченных деталей: а) 2 дефектных; б) хотя бы одна с дефектом.
4.Совет директоров состоит из 4 бухгалтеров, 3 менеджеров и двух инженеров. Планируется создать подкомитет из 3-х его членов. Найти вероятность того, что в подкомитет войдут:
а) 2 бухгалтера и менеджер; б) бухгалтер, менеджер и инженер; в) хотя бы один бухгалтер.
5.Надежность первого банка - 0,95, для второго – 0,8, для третьего – 0,85. Предприниматель совершил вклад во все три банка. Найти вероятность того, что предпринимателю вернут вклад: а) 2 банка; б) хотя бы один банк.
6. Вероятности получения прибыли с акций компаний А, В и С для акционера соответственно равны 0,6, 0,7, 0,5. Найти вероятность того,
что а) только один вид акций составит прибыль акционера, б) хотя бы один вид акций принесет доход их обладателю.
7. На курсах повышения квалификации бухгалтеров учат определять правильность оформления накладной. Для проверки преподаватель предлагает проверить 12 накладных, 5 из которых содержат ошибки. Наудачу выбирают 3 накладных. Найти вероятность того, что а) из 3-х накладных одна с ошибками; б) хотя бы одна с ошибками.
8. Вероятность того, что в определенный день торговой базе потребуется
двухтонная машина, равна 0,9, пятитонная - 0,7. |
Определить вероятность |
того, что торговой базе потребуется хотя бы одна |
автомашина. |
30
9.Вероятность того, что студент сдаст 1-й экзамен на положительную оценку – 0,9, второй – 0,8, третий – 0,8. Найти вероятность, что студент сдаст только 2-й экзамен на положительную оценку.
10.Станок работает при условии одновременного функционирования узлов А, В, С, которые работают независимо друг от друга. Вероятность поломки этих узлов 0,2, 0,3, 0,1 соответственно. Какова вероятность того, что станок выйдет из строя?
11. Технологический |
процесс |
состоит из нескольких |
операций. |
Вероятность того, что |
во время |
первой операции изделие |
получит |
повреждение, равна 0,1, а во время второй операции - 0,05. Какова вероятность того, что после двух операций изделие окажется поврежденным?
12. На рынок поступает продукция трех фабрик, причем продукция первой фабрики составляет 25% от всего объема поставок, продукция второй - 40% и третьей - 35%. Известно также, что средний процент нестандартной продукции для первой фабрики равен 3%, для второй - 2% и для третьей фабрики 1%. Взятый наугад образец продукции оказался стандартным. Какова вероятность того, что он изготовлен на второй фабрике?
13.Вероятность своевременного возвращения кредитов каждым из трех заемщиков банку независимы и соответственно равны: 0,6; 0,9; 0,7. Найти вероятность следующих событий:
а) только два заемщика возвратят кредит своевременно; б) хотя бы один из заемщиков возвратит кредит своевременно.
14.Среди 20 компьютеров, поступивших в ремонт в мастерскую, 12 – на гарантийном обслуживании. Мастер наудачу берет 2 компьютера для
ремонта. Найти вероятность того, что а) оба компьютера находятся на гарантийном обслуживании; б) хотя бы один на гарантии.
15. Заводом послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0,9, на второй - 0,95, на третьей - 0,8, на четвертой - 0,6. Найти вероятность того, что только на одной базе не окажется нужного материала.
16. Электрические лампочки изготавливаются на трех заводах. Первый из этих заводов поставляет 40% общего количества, второй - 35% и третий – 25%. Продукция первого завода содержит 80% стандартных ламп, второго - 90%, третьего - 98%. Все изготовленные лампочки поступают в
