
4051
.pdfМинистерство образования Российской Федерации
Хабаровская государственная академия экономики и права
Кафедра математики и математических методов в экономике
Моделирование рыночной экономики
Методические указания к практическим и лабораторным занятиям для студентов 4-5 курса специальности 061000 “Государственное
муниципальное управление”, 351000 “Антикризисное управление”, 061500 “Маркетинг”, 060600 “Мировая экономика“ дневной и
заочной форм обучения
Хабаровск 2003
2
В
Х12
Моделирование рыночной экономики. Моделирование спроса и предложения. Прогнозирование: Методические указания к практическим и лабораторным занятиям для студентов 4-5 курса специальности 061000 “Государственное муниципальное управление”, 351000 “Антикризисное управление”, 061500 “Маркетинг”, 060600 “Мировая экономика“ дневной и заочной форм обучения / Сост. Е.В.Мунгалова, Т.В.Ракова, И.Я.Шипицына. – Хабаровск: РИЦ ХГАЭП, 2003. - 24 с.
Рецензент к.э.н. доцент, зав.кафедрой экономической кибернетики ХГТУ К.Т.Пазюк
Утверждено издательско-библиотечным советом академии в качестве методических указаний для студентов
© Хабаровская государственная академия экономики и права, 2003
3
Введение
Методические указания посвящены курсу “Моделирование рыночной экономики”.
Методические указания разработаны для выполнения контрольных работ студентами специальности 061000 “Государственное муниципальное управление”, 351000 “Антикризисное управление”, 061500 “Маркетинг”, 060600 “Мировая экономика“ дневной и заочной форм обучения.
Освоение курса “Моделирование рыночной экономики” предполагает у студентов наличие знаний высшей математики и общих экономических дисциплин.
Вметодических указаниях раскрыты следующие темы: “Моделирование спроса и предложения”, “Методы прогнозирования”. Первая тема рассмотрена на основе сквозного примера. Вторая тема включает два раздела: метод сложения и метод умножения. Метод сложения описан с помощью модели с аддитивной компонентой, метод умножения – модели с мультипликативной компонентой. Решения сопровождаются краткими теоретическими изложениями вышеуказанных тем, что позволяет студентам самостоятельно освоить основные приемы моделирования.
Впособии приводятся примеры решения задач и задания для самостоятельного выполнения контрольных работ.
Авторами предложены варианты контрольных заданий. Вариант выбирается в соответствии с последней цифрой зачетки (0 соответствует 10 варианту).
4
1. Моделирование спроса и предложения
Пример 1. Изменение спроса на товар и предложения товара в зависимости от установленной цены представлено в табл.1.1:
Таблица 1.1 Объем спроса и предложения в зависимости от цены товара
|
Цена |
Спрос |
Предложение |
N |
(у.д.е. за шт.), P |
(тыс. шт. в месяц), Qd |
(тыс. шт. в месяц), Qs |
1 |
20 |
10 |
70 |
2 |
18 |
21 |
62 |
3 |
16 |
29 |
56 |
4 |
14 |
43 |
50 |
5 |
12 |
56 |
45 |
6 |
10 |
67 |
40 |
7 |
8 |
79 |
33 |
8 |
6 |
90 |
26 |
9 |
4 |
100 |
20 |
На основании приведенных данных:
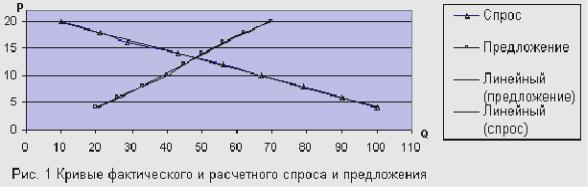
1.Построить кривые спроса и предложения.
2.Определить функции спроса и предложения, построить их графики.
3.Определить равновесную цену и равновесный объем продаж.
4.Описать ситуацию, которая установится на рынке, если цена товара составит 11 у.д.е. и 15 у.д.е.
5.Определить, возможно ли достижение точки равновесия. Построить паутинообразную модель, в качестве исходной цены взять значение 7 у.д.е.
6.Определить эластичность спроса и эластичность предложения относительно цены (в общем виде и по отдельным точкам значений цен).
7.Пусть на рынке имеется второй товар. Отмечено, что снижение цены на второй товар с 11 до 5 у.д.е привело к падению спроса на первый товар
с95 до 60 тыс.шт. в месяц. Определить перекрестную эластичность спроса. Решение. 1. Кривые спроса и предложения представлены на рис.1. Здесь
же приведены графики функций спроса и предложения.
1. Определим функции спроса и предложения. Предположим, что объемы спроса и предложения зависят от цены линейным образом (см. рис. 1).

5
В этом случае расчетные значения cпроса и но представить следующим образом:
ˆ
Qd a0 a1P,
ˆ ˆ
(Qd ) предложения (Qs ) мож-
(1.1)
ˆ s 0 1 (1.2)
Q b b P,
где a0, a1,b0, b1 - коэффициенты уравнений регрессии. Параметры a0, a1, b0, b1 определим, используя метод наименьших квадратов, согласно которому функция ошибок ( сумма квадратов отклонений фактических значений ряда от теоретических ) должна принимать минимальное значение. Для функции спроса функция ошибок имеет следующий вид:
|
N |
ˆ |
2 |
N |
2 |
|
(1.3) |
|
F(a0,a1 ) |
(Qdn |
(Qdn (a0 a1Pn )) |
min . |
|||||
Qdn ) |
|
|
|
|||||
n |
1 |
|
|
n 1 |
|
|
|
Минимальное значение функция ошибок принимает в точке, где ее частные производные равны нулю, т.е
F(a0,a1 ) |
|
0 |
|
a0 |
|||
(1.4) |
|||
F(a0,a1 ) |
|||
0 |
|||
a1 |
|
||
|
|||
Выполнив ряд преобразований, из системы (4) получим следующую систему:
|
|
|
N |
N |
|
|
|
||
a0 |
N |
a1 |
Pn |
|
Qdn |
|
|
|
|
|
|
|
n |
1 |
n |
1 |
|
|
(1.5) |
|
|
N |
|
N |
|
|
N |
|
|
|
|
|
|
2 |
|
|
|||
a |
0 |
|
P |
a |
P |
P Q |
dn |
, |
|
|
|
n |
1 |
n |
|
|
|||
|
|
n |
1 |
n 1 |
|
n |
1 |
|
|
где N – количество наблюдений.
В нашем случае N = 9, а вспомогательные суммы находим в табл.1.2.
|
|
|
|
|
|
|
|
Таблица 1.2 |
|
|
|
|
Вычисление вспомогательных сумм |
|
|
|
|||
N |
|
P |
Qd |
P2 |
P Qd |
|
Qs |
|
P Qs |
1 |
|
20 |
10 |
400 |
200 |
|
70 |
|
1400 |
2 |
|
18 |
21 |
324 |
378 |
|
62 |
|
1116 |
3 |
|
16 |
29 |
256 |
464 |
|
56 |
|
896 |
4 |
|
14 |
43 |
196 |
602 |
|
50 |
|
700 |
5 |
|
12 |
56 |
144 |
672 |
|
45 |
|
540 |
6 |
|
10 |
67 |
100 |
670 |
|
40 |
|
400 |
7 |
|
8 |
79 |
64 |
632 |
|
33 |
|
264 |
8 |
|
6 |
90 |
36 |
540 |
|
26 |
|
156 |
9 |
|
4 |
100 |
16 |
400 |
|
20 |
|
80 |
9 |
|
108 |
495 |
1536 |
4558 |
|
402 |
|
5552 |
n |
1 |
|
|
|
|
|
|
|
|

6
Подставив необходимые значения в систему (1.5) и решив ее, получим
a0 124,1 a1 5,758.Таким образом, функция спроса имеет вид: |
|
|
ˆ |
124,1 5,758P. |
(1.6) |
Qd |
||
Примечание: Полученное уравнение регрессии необходимо оценить с точки зрения его точности, надежности и значимости. Соответствующую теоретическую базу для этого можно найти в многочисленных источниках, посвященных корреляционно-регрессивному анализу данных. Мы ограничимся напоминанием некоторых формул и вычислением по ним значений для нашего примера.
Остаточная дисперсия (62ост), коэффициент детерминации (R2) и значение критерия Фишера (F) вычисляются следующим образом:
|
|
|
N |
|
|
|
|
ˆ |
|
2 |
|
|
|
||
|
|
|
|
(Qdn |
|
|
|
|
|
|
|
||||
|
62 ост |
|
|
|
Qdn ) |
|
|
|
|
||||||
|
n |
1 |
|
|
|
|
|
|
|
|
, |
|
(1.7) |
||
|
|
N |
m 1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
R |
2 |
|
6ост2 |
|
|
|
|
|
(1.8) |
||||
|
|
|
1 |
|
|
|
|
, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
6Q2 d |
|
|
|
|
|
|
||||
|
|
N |
ˆ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Qd ) |
/ m |
|
||||||||||||
|
|
|
|
(Qdn |
|
|
|||||||||
F |
|
n 1 |
|
|
|
|
|
|
|
|
|
, |
(1.9) |
||
|
N |
|
ˆ |
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(Qdn |
|
/(n |
m 1) |
|
|||||||||
|
|
Qdn ) |
|
|
|||||||||||
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где m – число независимых факторов, включенных в уравнение регрессии; Qd – среднее значение объема спроса; 6Qd2 – cмещенная оценка дис-
персии спроса.
В нашем случае 62ост = 1,998; R2 = 0,998; F = 3 983,75.
Аналогичные вычисления проведем для определения функции предложения. Искомая функция имеет вид:
ˆ |
8,267 3,033P. |
(1.10) |
Qs |
Оценки этой функции следующие: 62ост = 0,819; R2 = 0,997; F = 2 696,14.
Графики найденных функций спроса (1.6) и предложения (1.10) представлены на рис.1.
3. Равновесную цену Pe и равновесный объем продаж Qe определим, зная, что в точке равновесия совпадают цены спроса и предложения, а
также объемы спроса и предложения т.е. |
|
|
|||
Pe |
Pd |
Ps |
и |
(1.11) |
|
Qe |
Qd |
Qs . |
|||
|
|||||
|
|
||||
|
7 |
ˆ |
ˆ |
В нашем случае при Qd |
Qs из (1.6) и (1.10) имеем |
124,1 – 5,758 P = 8,267 + 3,033P. Отсюда равновесная цена Pe = 13,167.
Равновесный объем спроса и предложения составит (по уравнению
(1.6): Qe = 124,1 – 5,758 . 13,167 = 48,23 .
Проверим по уравнению (1.10): Qe = 8,267 + 3,033 .13,167 = 48,23 .
Таким образом, при установлении цены на уровне 13,167 у.д.е. объем спроса и предложения совпадут и составят 48,23 тыс.шт. товара в месяц.
4. При установлении цены на уровне 11 у.д.е. спрос составит Qd = 124,1 -5,758 . 11 = 60,762 тыс. шт. товара в месяц.
Предложение же при такой цене будет следующим:
QS = 8,267 + 3,033 . 11 = 41, 63 тыс. шт. товара в месяц. Таким образом,
возникает дефицит товара в 19,132 тыс.шт.
Установление цены выше равновесной, а именно на уровне 15 у.д.е., приведет к превышению объема предложения над спросом на 16,032
ˆ |
ˆ |
53,762). |
тыс.шт. (Qd |
37,73 ; Qs |
5. Наклон кривой спроса и предложения определяет возможность достижения точки равновесия. Так, “паутина" сходится, если a1 > b1 ; расхо-
дится, если a1 < b1 ; зацикливается, если a1 = b1 .
В нашем случае a1 > b1 возможно достижение точки равновесия.
Построим паутинообразную модель, исходя из заданной цены. По условию, цена предшествующего периода была установлена на уровне 7 у.д.е.,
что |
определило |
предложение |
данного периода |
равным |
29,498 |
тыс.шт. |
|||||||
ˆ |
8,267 3,033 7 |
29,498). |
При |
таком |
предложении |
цена |
спроса |
||||||
(QS |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ˆ |
||
устанавливается |
на |
уровне |
16,43 |
у.д.е. |
(из |
(1.6) |
P |
|
124,1 Qd |
= |
|||
5,758 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
124,1 29,498 ).
5,758
В свою очередь, цена P = 16,43 определит предложение последующего периода на уровне 58,098 тыс.шт. (из (1.10)), но потребитель такое количество товара согласен приобрести лишь при установлении цены
P |
124,1 |
58,098 |
11,463 у.д.е. |
Ориентируясь на цену 11,463 у.д.е., про- |
||
|
|
|
|
|||
5,758 |
|
|||||
|
|
|
|
|||
изводитель в дальнейшем выпустит на рынок 43,033 тыс.шт. товара, кото-
рые покупатель согласен приобрести по цене |
P |
124,1 |
48,033 |
14,079 |
||
|
|
|
||||
5,758 |
||||||
|
|
|
||||
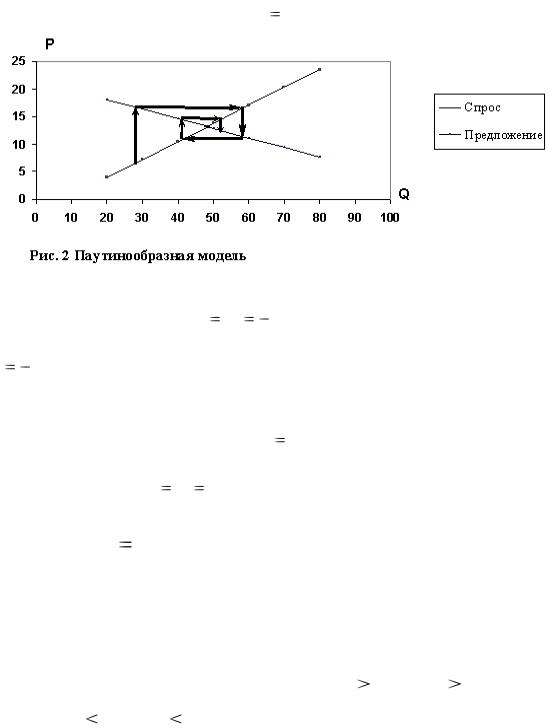
у.д.е. В конечном счете будет достигнута точка равновесия, определенная в п.3 задачи.
8
Траектория изменения цен и количества предлагаемого и требуемого товара представлена на рис.2.
6. Эластичность спроса относительно цены находится по формуле
E dp |
dQd |
: |
Qd |
. |
(1.12) |
|
|
||||
|
dP |
P |
|
||
В |
нашем |
случае |
dQ d |
|
a1 |
5,758.следовательно, |
в общем виде |
|||||||||
dP |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E dp |
5,758 |
|
P |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Qd |
|
|
|
|
|
|
|
|
|
|
|
|
||
Эластичность предложения по цене определяется по формуле |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
E sp |
dQs |
: |
Qs |
. |
(1.13) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
dP |
P |
|
||
Учитывая, что |
dQs |
|
b1 |
|
3,033, |
имеем эластичность |
предложения по |
|||||||||
dP |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
цене равную: Esp |
3,033 |
P |
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
Эластичность спроса и предложения показывает процентное изменение объема спроса или предложения при 1-процентном изменении цены. Эластичность спроса и предложения меняется в зависимости от того, в какой точке "объемно-ценового" пространства мы находимся.
Спрос (предложение) |
эластичен при |
E p |
1 ( |
E p |
1) и неэласти- |
||||
|
|
|
|
|
|
d |
|
s |
|
|
|
|
|
|
|
|
|
|
|
чен при |
E p |
1 ( |
E p |
|
1) . |
|
|
|
|
|
d |
|
s |
|
|
|
|
|
|
Значения эластичностей спроса и предложения по цене для разных уровней цен представлены в табл. 1.3.

9
Таблица 1.3
Эластичности спроса и предложения по цене
P |
Qp |
Qs |
|
P |
|
Edp |
5,758 |
P |
|
P |
|
Esp 3,033 |
P |
|
|
|
|
|
Qd |
Qd |
|
Qs |
Qs |
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
20 |
10 |
70 |
2,000 |
|
-11,516 |
|
0,286 |
0,867 |
|
|
||||
18 |
21 |
62 |
0,857 |
|
-4,935 |
|
0,290 |
0,881 |
|
|
||||
16 |
29 |
56 |
0,552 |
|
-3,177 |
|
0,286 |
0,867 |
|
|
||||
14 |
43 |
50 |
0,326 |
|
-1,875 |
|
0,280 |
0,849 |
|
|
||||
12 |
56 |
45 |
0,214 |
|
-1,234 |
|
0,267 |
0,809 |
|
|
||||
10 |
67 |
40 |
0,149 |
|
-0,859 |
|
0,25 |
0,758 |
|
|
||||
8 |
79 |
33 |
0,101 |
|
-0,583 |
|
0,242 |
0,735 |
|
|
||||
6 |
90 |
26 |
0,067 |
|
-0,384 |
|
0,231 |
0,700 |
|
|
||||
4 |
10 |
20 |
0,040 |
|
-0,230 |
|
0,200 |
0,607 |
|
|
||||
Из табл. 1.3 видно, что спрос остается эластичным, т.е. растет быстрее, чем падает цена, до тех пор пока цена остается в пределах от 20 до 12 у.д.е. Дальнейшее снижение цен происходит при более медленном нарастании спроса, т.е. спрос становится неэластичным.
Эластичность предложения по цене меняется слабо и остается при любой из указанных цен меньше 1, т.е. предложение в рассматриваемом диапазоне цен растет медленнее, чем цены.
7. Перекрестная эластичность спроса рассчитывается по формуле
|
Qi |
/ Qi |
|
|
Eij |
d |
d |
, |
|
Pj / Pj |
||||
|
(1.14) |
|||
|
|
|
||
где i, j – индексы товаров; Qdi – изменение объема спроса на i, товар
Pj – изменение цены j-го товара. ( |
Q Qt 1 Qt ; |
P Pt 1 Pt , где t и |
|||||
(t + 1) – периоды времени. |
|
|
|
|
|
|
|
Если Eij 0 , то товары взаимозаменяемы; если Eij |
0 ,то товары взаи- |
||||||
модополняемы; если Eij 0 , то товары независимы. |
|
||||||
В нашем случае Eij |
(60 |
95) / 95 |
0,368 |
0,675 |
, т.е товары взаимо- |
||
|
|
|
|
|
|||
(5 |
11) /11 |
|
0,545 |
||||
|
|
|
|
||||
заменяемы, и снижение цены второго (j-го) товара на 1% влечет за собой падение спроса на первый (i-й) товар на 0,675%.

10
2. Методы прогнозирования
Прогнозирование деловой активности является важным инструментом в процессе принятия решений. Способность составить надежные оценки будущих показателей, например, спроса на товары, стоимости материалов, производственной себестоимости и затрат на рабочую силу, обеспечивает многим предприятиям преимущество в конкурентной борьбе. Такие прогнозы можно использовать при принятии тактических и стратегических решений.
Существуют методы, которые используют приемы анализа временных рядов.
Ряд значений, взятый за временной период, называется временным рядом. Каждое значение временного ряда может состоять из следующих составляющих: тренда, циклических, сезонных и случайных колебаний. Эти составляющие можно описать следующим образом.
Тренд. Данную составляющую можно рассматривать в качестве общей направленности изменений определенных значений, взятых на протяженном отрезке времени. Тренд можно выделить с помощью таких методов как метод регрессии, метод скользящих средних, метод центрированных скользящих средних, метод экспоненциального сглаживания.
Циклические колебания. Помимо тренда значений часто очевидно присутствие циклической составляющей. Эти составляющие показывают колебания относительно линии тренда для периодов свыше одного года.
Сезонные колебания. Многие ряды значений демонстрируют периодичность колебаний на протяжении года или более. Сезонные колебания можно вычленить после анализа тренда и циклических колебаний.
Случайные колебания. Эти составляющие представляют собой случайные элементы, которые обычно невозможно предугадать.
Сезонная составляющая может быть очевидна во многих случаях, где задействованы финансовые и экономические показатели. На последующих примерах мы рассмотрим два метода, которые часто используются при оценке сезонных колебаний.
2.1 Метод сложения
Метод сложения используется в случаях, когда сезонные составляющие постоянны по всему анализируемому временному периоду (см. рис. 3). При этом значение временного ряда можно представить как сумму тренда и сезонной составляющей. В общем виде этот метод можно описать следующей формулой: X i Ti Si ,
где X i - фактическое значение в периоде i ; Ti - тренд в периоде i ;
Si - сезонное отклонение в периоде i .
