Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5666.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

2.89 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

43.Какие признаки можно применять для нахождения области сходимости степенных рядов?

44.Какой вид имеет формула для определения радиуса сходимости степенного ряда, являющаяся следствием предельного признака Даламбера?

45.Какой вид имеет формула для определения радиуса сходимости

степенного ряда, являющаяся следствием предельного признака Коши?

46.На каких промежутках степенные ряды сходятся равномерно?

47.Что можно сказать о мажорируемости степенного ряда?

48.На каком множестве сумма степенного ряда является непрерывной функцией?

49.Может ли сумма степенного ряда быть непрерывной функцией на каком-нибудь из промежутков R, R , R, R , R, R , , , если

ряд на соответствующем промежутке сходится?

50.В каких областях степенной ряд можно почленно интегрировать?

51.Можно ли степенной ряд почленно дифференцировать? В каких точках это возможно?

52.Что можно сказать об области сходимости ряда, составленного из производных некоторого степенного ряда (продифференцированного ряда)?

5. Ряды Тейлора и Маклорена

Если функция является суммой степенного ряда в каком-нибудь промежутке, то говорят, что она разлагается в степенной ряд в этом промежутке. Для многих приложений важно уметь разлагать данную функцию в степенной ряд вида (24) или (25).

Пусть функция f (x) разлагается в некотором промежутке R, Rв степенной ряд вида (24), то есть имеет место равенство

f x a	a x	a	2	x2	a x3	a	n	xn	(31)
0	1		2		3		n

(будем считать, что R является					и радиусом сходимости						степенного
ряда (31)).
Справедливо утверждение: представление функции в виде (31) един-
ственно, причём
	an			f n 0	n		0,1, 2, ... .				(32)
	an			n !	n		0,1, 2, ... .				(32)
				n !
При этом использовано обозначение					f 0		0	f 0 .
Доказательство этого утверждения основано на теореме 14 и
замечании 24.
Продифференцировав ряд (31) почленно, получим
f x a	2a	2	x	3a x2	4a	4	x3	na	n	xn 1	(33)
1		2		3		4			n

(радиус сходимости этого ряда также равен R ). Степенной ряд (33) по замечанию 24 снова можно дифференцировать, при этом радиусом сходимости снова будет R . После дифференцирования получим, что

f x 2a

2 3a x

3 4a

1 na

xn 2

(34)

Положим в равенствах (31), (33), и (34) x

0 ; получим

f 0 , a1

f 0

, a2

f 0

Таким образом, были найдены первые три коэффициента разложения (31), при этом они соответствуют формуле (32).

Процесс почленного дифференцирования ряда (31) можно неограниченно продолжить. Увидим, что все коэффициенты ряда (31) определяются формулами (32).

Разложение функции f (x) в ряд (31) единственно, так как коэффи-

циенты an	этого разложения определяются единственным образом
формулами (32).
Замечание 25. Если функция		f (x)	в промежутке x0	R, x0	R
разлагается в ряд вида (26), то есть имеет место равенство
f x	a0 a1 x x0 a2 x	x0 2	an x x0 n	,	(35)

то это разложение единственно, причём коэффициенты определяются равенствами

an	f n	x0		n	0,1, 2, ... .		(36)
	n !

Здесь использовано обозначение		f	0 x		f x	. Для нахождения коэф-
			0		0

фициентов в ряде (35) и в продифференцированных рядах надо полагать

x x0 .

Напомним, что функция f (x)

называется бесконечно дифференци-

руемой, если у неё существуют производные любого порядка.

Определение 12. Ряд вида

f 0

n 0

f n 0

(37)

n !

называется рядом Маклорена функции

f (x) .

Такой ряд можно образовать для любой бесконечно дифференциру-

емой функции в точке x

0 . Ряд (37) есть степенной ряд по степеням пе-

ременной x ; его коэффициенты называют коэффициентами

Мак-

лорена.

Определение 13. Ряд вида

f (x

)

f (x

)

f (n) (x )

f (x )

(x x

)

(x x

f (n) (x )

x )n

(38)

n 0

называется рядом Тейлора функции

f (x) .

Ряд (38) является степенным рядом по степеням двучлена x

x0 и

может быть образован для любой бесконечно дифференцируемой функции f (x) в точке x0 . Его коэффициенты называются коэффициентами Тейлора.

Ряды (37) и (38) имеют данное название независимо от того, в какой области они сходятся и является ли функция f (x) , которая задаёт коэффициенты этих рядов, их суммой.

Ряд (37) является частным случаем ряда (38) ((37) получается из (38) при x0 0 ). Временно ограничимся изучением ряда (38). Дальнейшие рас-

суждения относительно ряда (38) читатель должен самостоятельно перенести на ряд (37).

Замечание 26. Утверждение, высказанное в замечании 25, можно сформулировать следующим образом: всякий сходящийся в x0 R; x0 Rстепенной ряд (25) есть ряд Тейлора функции, являющейся

его суммой.

Ряд Тейлора (38), как всякий степенной ряд по степеням двучлена x x0 , сходится в точке x x0 . Возникает вопрос: сходится ли этот ряд где-нибудь кроме этой точки? Возникает и второй вопрос: если ряд (38) сходится на некотором промежутке, то будет ли функция f (x) , с помощью которой вычислены коэффициенты ряда, его суммой? Приведём пример функции, ряд Тейлора которой сходится, но его сумма не представляет саму эту функцию.

Пример 27. Рассмотрим функцию

f x		x	x0	2
	e	x	x0		при x	x0 ,
	e				при x	x0 ,
	0				при x	x0.

Можно показать, что эта функция непрерывна и, более того, бесконечно

дифференцируема.			По определению f x0 0 ; можно показать, что для
всех n и	f	n x	0 . Поэтому ряд Тейлора этой функции сходится для
		0

всех x к нулю, тогда как сама f xпринимает значение 0 только в точке x x0 .

На поставленные вопросы можно ответить с помощью формулы Тейлора из дифференциального исчисления функций одной переменной.

Для

любой функции f x

определённой в

окрестности

x0 R; x0

точки x0

и имеющей в ней производные до

n 1 -го по-

рядка включительно, справедлива следующая формула Тейлора:

f x

f (x )

f (x0 )

(x x )

f (x0 )

(x x )2

f (n) (x0 )

)n r*

x .

(39)

При этом функция rn* xназывается остаточным членом формулы Тейлора. Её можно записать в нескольких формах. В форме Лагранжа эта функция имеет вид

n 1

n 1,

(40)

n 1 !

где число c заключено между x0

и x . Это число c можно записать в виде

c x0 Θ x x0 , 0 Θ 1.

Равенство (39) кратко записывается в виде f x

x ,

где P x

f (x )

f (x

)(x

)

f (n) (x0 )

называется многочленом (полиномом) Тейлора n -й степени. Очевидно,

что Pn x Sn 1 x , где Sn 1 xесть n 1 -я частичная сумма ряда Тейло-

ра (38). Поэтому формулу Тейлора для функции f xможно записать следующим образом:

f x S	n	1	x	r*	x .	(41)
	n	1		n
Отметим, что остаточный член r* x		в формуле Тейлора для функции				f x
n

не обязательно является остатком ряда Тейлора этой функции. Поэтому из сходимости ряда Тейлора, составленного по данной функции, ещё не следует его сходимость именно к этой функции (см. пример 27).

Так как формула Тейлора (39) верна для бесконечно дифференцируемой функции, то на основании (40), (41) получим ответ на поставленные

выше вопросы.
Теорема 15. Ряд Тейлора (38), составленный по функции		f x , схо-
дится на промежутке x0 R, x0	R и имеет своей суммой эту функцию
тогда и только тогда, когда
lim	r* x 0	(42)
n	n
n

в этом интервале.

Доказательство. Пусть ряд Тейлора (38) сходится к

f x

в интерва-

ле x0

R, x0

R . Это означает (см. (13)), что

f x

lim

Sn x . Посколь-

ку и lim

1 x

f x , то (см. (41))

lim

f x

lim

x f

f x 0 .

Равенство (42) установлено.

Обратно, пусть выполняется равенство (42). Так как

(см. (41)), то

lim

f x

n 1

lim r* x

0 . Следовательно,

lim

1 x

x .

Выполняется и равенство

lim

Sn x

x . Это означает,

что ряд Тейлора

(38) сходится, а его суммой на рассматриваемом интервале является функ-

ция f x(см. (13)).

Замечание 27. Так как

* x

в форме Лагранжа имеет вид (40), то

равенство (42) можно записать в виде

lim

x0 n

0 .

(43)

1 !

Пример 28. Требуется разложить функцию

3x2

7 по

степеням x

1 . Здесь x0

1. Найдём

x0 ,

, f

, ... :

f 1

11 ,

f x

4x3

6x ,

f x0

f 1 4 6 10 ;

f x 12x2

6 ,

f x0

f 1 12 6 18 ;

f x

24 x ,

f 1 24 ;

f 4 x

24 ,

4 x

f 4 1 24 ;

f 5 x

0 ,

5 x

f 5 1 0 .

Очевидно,

что для n

0 и тогда r* x

0 .

Поэтому

3x4

10(x

1)2

(x 1)3

(x 1)4

11 10(x 1) 9(x 1)2

4(x

1)3

(x 1)4 .

Если бы эту функцию разлагали б по степеням x ( x0

0 ),

то полу-

чили бы тот же самый многочлен.

Пример 29. Требуется разложить в ряд Тейлора функцию

e x в

промежутке

, 2

Так как функция

e x

бесконечно дифферен-

цируема и

при любом n ,

то согласно (40) остаточный член

r* x

формулы Тейлора можно записать в виде

e2 Θ x

2 n

1 .

1 !

Так как

, 0

1, то согласно последнему равенству

r* x

e2 .

1 !

следовательно, lim r* x

Так как

lim

то

lim

0 и,

1 !

Поскольку выполнено условие (42), то по теореме 15 ряд Тейлора функции

y e x с центром в точке x0					2 имеет вид
e x e2	e2	(x 2)	e2	(x	2)2 ...	e2	(x 2)n ...		e2	(x 2)n

1!			2!			n!		n 0 n!

и имеет своей суммой в рассматриваемой окрестности функцию ex . Проверка условий (42) или (43) может оказаться трудной задачей.

Укажем достаточный признак сходимости ряда Тейлора к своей функции, условия которого иногда оказываются более удобными для их проверки,

чем условия (42) или (43).
Теорема 16. Если все производные функции			f x ограничены в
промежутке x0	, x0	одним и тем же числом M	0, т.е.

f (n) (x)

M , n

1, 2,

...,

(44)

то ряд Тейлора этой функции сходится к ней в этом промежутке.

Доказательство. Согласно теореме 15 достаточно

показать,

что

lim

0. По условию данной теоремы для любого n имеет место не-

равенство

f (n) (x)

M . Тогда согласно (40)

f (n 1) (c) (x x

)n 1

(x x0 )n 1

x x0

n 1

n 1 .

1)!

(n 1)!

1)!

lim r*

Так как

lim

0 ,

то lim

0 и, следовательно,

1)!

Теорема доказана.

Для разложения функции

в ряд Маклорена (37)

можно следо-

вать следующим пунктам:

найти производные f

x ,

x , ..., f

n x , ...;

найти значение функции и производных в точке x0

0 ;

3)составить ряд (37) для заданной функции и найти его интервал сходимости;

4)найти промежуток, в котором остаточный член ряда Маклорена

r* x

0 при

. Если такой промежуток существует, то в нём функ-

ция f

x и сумма ряда Маклорена совпадают.

Укажем формулы разложения в ряд Маклорена следующих элемен-

тарных функций:

1) ex

;

(45)

n 0 n!

n x2n 1

( 1)n x2n 1

2) sin x

(

; (46)

(2n 1)!

(2n

1)!

3) cos x

(

n x2n

( 1)n x2n

, x

;

(47)

(2n)!

4)ln (1 x)

5)arcsin x

6)arctg x

7)(1 x)

	x2		x3		n 1 xn				( 1)n 1 xn		1, 1 ; (48)
x				( 1)						, x
x				( 1)						, x
	2	3				n	n	1	n
							n	1

	1	x3		1		3		x5					1 3 5			x7	1 3 5 ... (2n							1)		x2n	1	,
	2	3		2		4				5			2	4 6		7			2 4 6 ... (2n)							2n	1	,
	2	3		2		4				5			2	4 6		7			2 4 6 ... (2n)							2n	1
														x	1, 1 ;													(49)
x3			x5						( 1)n x2n 1									( 1)n x2n 1
																							,	x	1, 1 ;			(50)
3		5										2n		1			n 1		2n	1			,	x	1, 1 ;			(50)
3		5										2n		1					2n	1

		x		(			1)			x	2				(		1) ... (		n	1)	x	n			,
1!		x			2!					x							n!				x				,
1!					2!												n!

1; 1 ,

если

1; 1 , если

(51)

1; 1 ,

если

1, 1 .

(52)

1 x

Разложения функций 1) – 9) можно принять за аналитическое опре-

деление этих функций.

Докажем формулу (45). f (x)

ex .

1) f (x)

e x ,

f (x)

ex , f

(x)

e x , ...,

f (n) (x)

ex , … .

2) f (0)

(0)

f (0)

1, …, f (n) (0)

1, … .

3) e x ~1

(знак ~

означает формальное разложение

функции в ряд Маклорена).

lim

1)!

lim

1)!

т.е. ряд сходится на интервале

4) Для всех x

имеем

f (n) (x)

M , т.е. все производные

в этом интервале ограничены одним и тем же числом

e . Следова-

тельно, по теореме 16 ряд сходится к ex для любых x из , . В силу

произвольности

он сходится к ex на всей числовой оси.

Докажем формулу (46). f (x)

sin x .

(x)

cox x ,

f (x)

sin x ,

(x)

cos x ,

f 4 (x)

sin x , … , или

(x)

sin

(x)

sin

f (x)

sin x 3

4 (x) sin

, … ,

f (n) (x)

sin

, … .

0, n

0, 2, 4, 6, ... ,

f (n) (0)

sin

3, 7, 11, ... ,

1, 5, 9, ... .

sin

x ~ x

( 1)

n x2n 1

(2n

1)!

Можно проверить, что данный ряд сходится на всей числовой оси, т.е. при всех x , .

4) Любая производная функции f (x) sin x по модулю не превышает 1:


f (n) (x)	sin( x n	)	1	. Следовательно, по теореме 16 ряд (46) сходит-

	2

ся к функции sin x на всей числовой оси.

Докажем формулу (47). f (x) cos x .

Доказательство данной формулы можно провести аналогично доказательству формулы (46). Но проще воспользоваться теоремой 14 о почленном дифференцировании степенных рядов. Продифференцировав

почленно ряд (46), получим:

cos x

(

1)n

x2n

, x

(2n)!

Докажем формулу (52). f (x)

Рассмотрим ряд 1

x x2

при x

1, 1 . Это геометри-

ческий ряд с первым членом u1

1 и знаменателем q

x . Известно, что

данный ряд сходится при			x	1, 1			(	q	1) и его сумма равна								1	(см.
																	1

																1	x
		f x	1			f		x		2			f x		6	1	x
пример 7). Так как			1		,					2		,			6		, … , то

			1	x 2						1 x 3					1 x 4
этот ряд является рядом Маклорена для функции													1	.

											1		x
Докажем формулу (48). f (x)							ln(1			x) .
В разложении (52) введём замену x							t , получим
1		1 t	t 2	t3					( 1)n t n					, t	1, 1 .


1	t

Воспользуемся теоремой 13 о почленном интегрировании степенных ря-

дов. Проинтегрируем это равенство почленно от 0 до x

1 :

x 1

ln(1

ln(1 x) ;

0 1

x 1

x dt

xt dt

xt 2 dt

xt3 dt

( 1)n xt n dt

01 t

t 2

t 4

n t n 1

n 1

n tn

т.е. ln(1

(

1)n

при x

1, 1 .

Отметим без доказательства, что данное разложение справедливо также

для x 1, т.е. ln 2 1			1	1	1	.

			2	3	4
			2	3	4
		Докажем формулу (50). f (x)				arctg x .
В разложении (52) введём замену x							t 2 и проинтегрируем по t от 0 до x
	x	1 :
	x	1 :
			1		1 t 2	t 4	( 1)n t 2n	,

			1	t 2
			1	t 2

														x			1								0x
																											arctg x ,
																				dt			arctg t
													01						t 2	dt			arctg t
													01						t 2
				x	1					x				x						x									x
					1			dt				dt			t 2 dt					t 4 dt						(		1)n		t 2n dt

			01			t 2
			01			t 2				0			0							0								0
										x			x3				x5				(			1)n			x2n	1		.
										x			3				5				(			1)n			2n	1		.
													3				5										2n	1
Т.е. arctg x					x			x3			x5								( 1)n				x2n 1			,		x		1, 1 .
Т.е. arctg x					x			3				5							( 1)n				2n	1		,		x		1, 1 .
								3				5											2n	1
		Можно показать, что данное разложение верно при																													x	1;			причём
при x 1 получим												1	1				1			.

									4				3				5
		Докажем формулу (51). f (x)																			(1			x)	,			R .
1)	f	(x)	(1				x) 1,					f	(x)				(			1)(1				x)		2 , ... ,
	f (n) (x)					(		1)(					2) ... (							(n	1))(1					x)		n ,		n N .
2)	f	0	1,		f	(0)				,		f	(0)							1 , … ,
	f (n) (0)							1					2							n		1 , … .
3) (1		x)	~ 1					x		(			1)			x	2				(			1)(				2)		... (	n	1)		x	n		.
3) (1		x)	~ 1					x				2!				x												n!						x			.
												2!																n!
4) Вычислим радиус сходимости по формуле (28):
R		lim		an				lim									1			2					n 1 n 1 !						lim			n 1			1,
				an													1			2					n 1 n 1 !									n 1
				an 1								n!					1				2						n 1			n					n
		n		an 1				n				n!					1				2						n 1			n	n				n
т.е. составленный для функции f																				x	1			x			ряд сходится на						интервале
	1, 1 .
		Можно показать,											что на интервале												(		1, 1) остаточный член r*										x
																																				n
стремится к нулю при n																	.
		В граничных точках x																1 ряд (51) может сходиться или расходить-
ся в зависимости от показателя степени																											(разбор этих случаев можно
найти в [6]).

	Замечание 28. Ряд (51) называется биномиальным. Если																																														n N ,
то все члены ряда с n																	1 -го номера равны 0, т.к. содержат множитель
n 0. В данном случае ряд (51) будет представлять собой известную
формулу бинома Ньютона:
			(1				x)	n				1			n	x			n(n						1)				x	2						n(n				1)		... 1		x		n

													1!											2!																n!
													1!											2!																n!
					1						n	x			n(n			1)						x	2			n(n 1)(n									2)		x	3			x	n	.
					1					1!		x				2!								x						3!									x				x		.
										1!						2!														3!
	Докажем формулу (49). f (x)																													arcsin				x .
Положив в формуле (51)																							1			и заменив x на														t 2 , получим равенство
Положив в формуле (51)																		2								и заменив x на														t 2 , получим равенство
																		2
					1								1				t 2					1 3					t 4					1 3 5						t 6				, (x				1, 1 ) .
																2		2							4					2			4	6
					1				t	2
										2

Тогда
															x			1								dt			arcsin				t		x			arcsin				x ,
															x


																																			0
																1					t 2

													0
			x		1				dt					x dt					1		x t 2dt										1 3		x t 4dt								1 3 5		x t 6dt


			0 1 t 2										0					2 0												2 4 0										2 4 6 0
x		1		x3		1 3 x5												1 3 5											... (2n					1)				x2n 1						при x			1, 1 .
x		2		3		2		4				5								2					4		6			... (2n)								2n		1				при x			1, 1 .
		2		3		2		4				5								2					4		6			... (2n)								2n		1

Можно показать, что данное равенство справедливо и при x 1. Свойства степенных рядов вместе с разложениями (45) – (52) могут

быть использованы при разложении некоторых других функций в ряд Маклорена.

Пример 30. Требуется разложить функцию f (x)		1	в ряд

	x2	2x 2
	x2	2x 2

Тейлора по степеням выражения x 2 и найти область сходимости полученного ряда.

Представим данную функцию в виде суммы простейших дробей:

1	1			А	В	А(х 1) В(х 2)	.
х2 3х 2
		(х 2)(х 1)		х 2	х 1	(х 2)(х 1)
			64

Тогда 1											А(х	1)			В(х					2) . Из этого равенства при x 1 получаем B																																	1,
при x								2 получаем A 1. Таким образом,
											1				1						1						1									1										1

							х2				3х 2				х 2 х 1 х 2 4 х 2 3																										4					х 2				1
																																									4							4		1
																																																4
																	1										1						1			1					1				.

															3				х		2		1				3				1		х		2	4		1				х		2
																			х		2						3									4
																																			3						4
																				3
																				3
Воспользуемся разложением (51). Тогда
					1						1	х 2						х 2 2																x 2			n			при								x 2			1,		т.е.
					1							х 2						х 2 2																x 2			n											x 2

1					х			2				3					3											n			0				3													3
					х			2				3					3																		3													3
					3
					3
	x				2			3,
	x				2			3,
					1						1	x 2						x 2 2																x 2			n			при								x 2			1,		т.е.
					1							x 2						x 2 2																x 2			n											x 2

1					x			2				4					4											n			0				4													4
					x			2				4					4																		4													4
					4
					4
	x				2			4 .
	x				2			4 .
Окончательно получаем
								1						1				x 2 n							1							x 2 n									1							1		(x		2)n

				x2				3x 2						3 n 0			3								4 n 0						4						n 0 3n 1										4n 1
				x2				3x 2						3 n 0			3								4 n 0						4						n 0 3n 1										4n 1
при						x		2			3, т.е. при x											5, 1 .
							Пример 31. Разложим в ряд Маклорена функцию																																					f			x		3x . Так как
3x							eln 3x					ex ln 3 ,					то заменяя										x		на xln 3							в разложении (51), получим
3		x			1				x ln 3					x ln 3 2										x ln 3 n											1		ln 3		x				ln 2	3		x		2
3					1						1!		2!													n!									1		1!		x				2!			x
											1!		2!													n!											1!						2!
			ln n 3					x		n						ln n 3				x	n	,	x						,						.
					n!			x						n	0		n!			x		,	x						,						.
					n!									n	0		n!
							Пример 32. Разложим в ряд Маклорена функцию																																									f x			ln	4	x .
Так как f (x)													ln( 4 x)							ln 4 1						x				ln 4					ln 1					x			, то будем разлагать

																									4														4
																									4														4

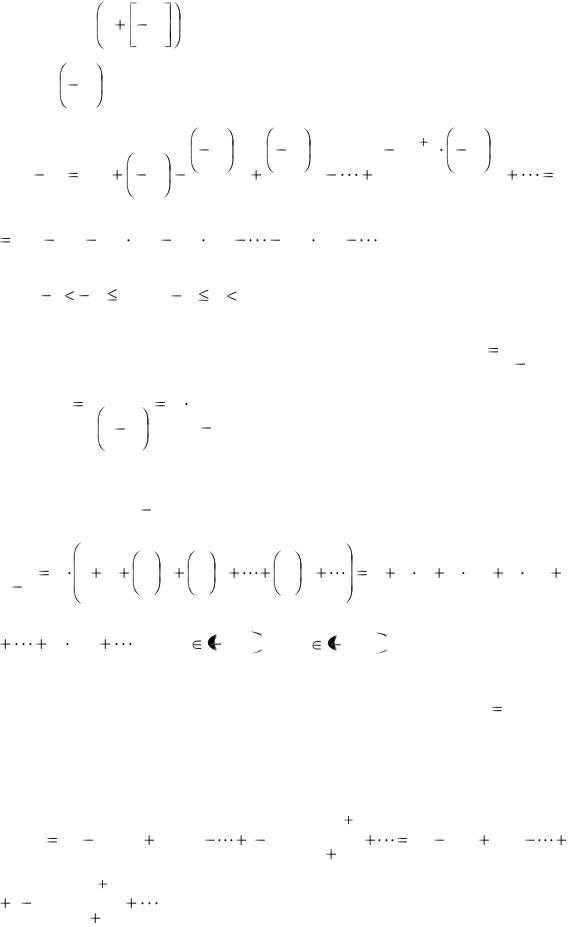
функцию						ln			1							x				. Воспользуемся формулой (48), в которой x заме-

															4
															4
ним на							х			. Получим:
ним на						4				. Получим:
						4
																							x	2			x		3				( 1)n 1		x		n
																x
ln( 4			x)			ln 4															4				4									4
																					4				4									4

															4						2				3									n
															4						2				3									n
			1						1					x2				1				x3			1					xn
	ln 4					x																									,
	ln 4					x			42									43								4n					,
			4						42						2			43			3					4n				n
если			1					x			1, т.е.							4				x		4.

						4
						4
			Пример 33. Разложим в ряд Маклорена функцию f (x)																																2				. Так

																																				3 x
как		f (x)							2									2			1			, то воспользуемся формулой (52) для разло-

						3 1							x					3 1					x
													x
																					3
												3
												3
жения функции															1			. Заменяя x на										x	, получим:
жения функции																	x	. Заменяя x на											, получим:
												1					x								3
												1			3
															3
	2				2	1				x					x 2						x 3					х n						2 2 х 2 х2						2 х3

	3 x 3								3 3												3				3					3 3 3 3 32							3 3
	3 x 3								3 3												3				3					3 3 3 3 32							3 3
				2		хn								, где					х		1, 1				или х					3, 3 .
			3			3n								, где				3			1, 1				или х					3, 3 .
			3			3n												3
			Пример 34. Разложим в ряд Маклорена функцию f (x)																																		sin x5
																																								. Сна-
																																								. Сна-
																																							х

чала разложим в ряд sin x5 . Воспользуемся формулой (46); заменив в ней x на x5 , получим

sin x

(х5 )3

(х5 )5

n (х5 )2n 1

5 х15

х25

( 1)

(2n 1)!

( 1)

n х10n

. Разделив почленно этот ряд на х, получим

(2n

1)!

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20222.72 Mб15661.pdf
#
13.11.20222.72 Mб15662.pdf
#
13.11.20222.81 Mб25663.pdf
#
13.11.20222.82 Mб65664.pdf
#
13.11.20222.86 Mб85665.pdf
#
13.11.20222.89 Mб15666.pdf
#
13.11.20222.92 Mб25667.pdf
#
13.11.20222.96 Mб45668.pdf
#
13.11.20222.96 Mб25669.pdf
#
13.11.20223.01 Mб15670.pdf
#
13.11.20223.01 Mб15671.pdf