5630
.PDF
Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической формах.
1. Геометрическое условие равновесия
Так как главный вектор R системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то R может обращаться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, т.е. многоугольник сил замкнут.
Следовательно, для равновесия сходящейся системы сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут.
2. Аналитические условия равновесия
Поскольку модуль равнодействующий сходящихся сил определяется как R
= 
R2 x R2 у R2 z , то равнодействующая сила будет равна нулю только в том случае, если одновременно Rх = 0, Ry = 0, Rz = 0.
Следовательно, для равновесия сходящейся системы сил необходимо и достаточно, чтобы сумма проекций сил, действующих на тело, на оси координат была равна нулю.
n |
n |
n |
|
Fix 0; |
Fiy 0; |
Fiz 0 . |
(1) |
i 1 |
i 1 |
i 0 |
|
Уравнения (1) выражают аналитические условия равновесия пространственной сходящейся системы сил.
Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил, условия равновесия в этом случае
Fix 0; Fiy 0 . (2)
Из условия равновесия в геометрической форме следует, что если тело находится в равновесие под действием трѐх сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке – теорема о трѐх силах.
Примеры на применение уравнений равновесия сходящейся системы сил Пример 1. Балка АВ поддерживается в горизонтальном положение
невесомым стержнем ВD, наклонѐнным к балке под углом α = 30º, и шарнирно неподвижной опорой в точке А; крепления в точках А, В и D шарнирные (рисунок 17,а). Определить реакцию шарнира А и усилие, растягивающее стержень ВD, если вес балки 100кН, балка однородная.
21
а)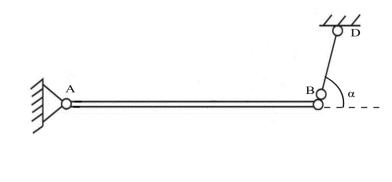 
б)
в)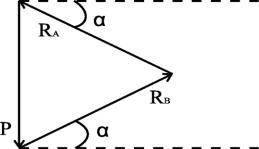 
Рисунок 17 – Положение балки АВ
Порядок решения задач статики следующий:
1.Выбирают объект равновесия.
2.Показывают задаваемые силы, действующие на выбранный объект.
3.Связи заменяют их реакциями.
4.К полученной системе сил применяют условия равновесия, из которых находят искомые величины.
Выбираем объект равновесия – балка АВ. Показываем задаваемые силы – вес балки Р, балка однородная, поэтому сила Р приложена в центре балки (рисунок 17,б). Действие связей в точках А и В заменяем их реакциями. Реакция Rв стержня BD направлена вдоль стержня. Реакция Ra шарнирно-неподвижной опоры неизвестна по величине и направлению. Но, так как, балка АВ находится
вравновесии под действием 3 сил, то линии их действия должны пересекаться в
22
одной точке (теорема о трѐх силах). Такой точкой является точка С – точка пересечения линии действия сил Р и Rв (рисунок 17,б). Для нахождения реакций RА и RВ применим геометрическое условие равновесия плоской сходящейся системы сил: треугольник сил должен быть замкнут (рисунок 17,в). Из
рассмотрения рисунка следует, что
Вычисляем:
|
1 |
1 |
|
1 |
|
|
||
RA |
|
100 |
|
|
|
|
|
100 кН ; |
2 |
sin 60 |
|
|
|
||||
3 |
||||||||
RB Rα 100 кН . 
3
|
|
|
|
|
|
и R |
|
|
1 |
P |
. |
||
|
|
|
|
||||||||||
R |
|
|
|
R |
|
|
|
||||||
|
|
|
|
|
A |
|
|||||||
|
А |
|
|
|
|
В |
|
|
|
2 sinα |
|
||
Следует обратить внимание, что с изменением угла α меняются реакции Rа и
Rв в пределах P 2 при α = 90° до ∞ при α = 0°.
Пример 2. Определение усилий в стержнях плоской фермы методом вырезания узлов.
Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция (рисунок 18).
Рисунок 18 – Схема плоской фермы Точки, в которых сходятся оси стержней, называются узлами фермы.
Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположение по нижнему контуру – нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные – раскосами.
Если нагрузка приложена в узлах фермы и отсутствует трение в шарнирах, то все стержни работают на растяжение или сжатие. За счѐт этого ферма может выдержать большие нагрузки при относительно малом собственном весе.
Определим усилия в стержнях фермы, которая является стрелой подъѐмного крана (рисунок 19). Поднимаемый груз р = 100кН.
23
Рисунок 19 – Стрела подъѐмного крана Метод вырезания узлов заключается в следующем: мысленно вырезают узлы
фермы; прикладывают к ним соответствующие внешние силы и реакции стержней, а затем составляют уравнения равновесия сил, приложенных к данному узлу. Для однозначности полагают, что все стержни находятся в растянутом состоянии и усилие в них направлены от узла. Последовательность рассмотрения узлов определяется количеством неизвестных, которое не должно превышать количество уравнений равновесия.
Для формы на рисунке 20 таким узлом является узел С.
а) 
, б) 
,
в) 
Рисунок 20 – Схема узла С (а), узла D (б), узла Е (в)
Составляем уравнения равновесия для узла С (рисунок 20,а).
X i 0 ; |
S 1 cos S 2 0; |
Yi 0 ; |
S1 sin p 0 ; |
|
S 1 p sin ; |
|
S 2 S1 cos Pctg . |
|
24 |
Составляем уравнения равновесия для узла D (рисунок 20, б).
X i |
0; |
S 3 cos S 1 cos 0 ; |
|
|
|
|
|
|
|
P |
; |
|
|
S 3 |
S 1 |
sin |
|
Yi |
0 ; |
S 3 sin S1 sin S 4 |
0 ; |
|
|
|
|
|
S4 0 . |
|
|
Составляем уравнения равновесия для узла Е (рисунок 20, в)
Xi |
0 ; |
S 2 |
S 6 |
S 5 cos 0 ; |
Yi |
0 ; |
S 4 |
S 5 |
cos 0 ; |
S 5 0, т.к. S 4 0 ;
S 6 S 2 .
Аналогичным образом можно найти усилия в остальных стержнях этой формы. Определим численные значения в стержнях 1 – 6.
|
|
|
sin |
|
|
a |
|
|
|
1 |
|
; |
ctg |
3a |
3 ; |
|
|
|
|
|
|
|
|
|
|
|
a |
||||||
|
|
|
a2 3a 2 |
10 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
300kH ; |
|
|
|
||||||
S1 |
100 10 |
320kH ; |
|
|
S2 |
|
|
|
||||||||
S3 |
320kH ; |
S4 0; S5 |
0; |
S6 |
300kH . |
|
|
|
||||||||
Анализируем полученные результаты:
1)стержни верхнего пояса находятся в растянутом состоянии, а нижнего пояса в сжатом состоянии, а
2)стержни 4 и 5 называются «нулевыми» поскольку S4 = S5 = 0. В идеале такие стержни не нужны, но их отсутствие может лишить жѐсткости конструкцию. В практике «нулевые» стержни выполняются более тонкими или из менее прочного материала.
Условия равновесия пространственной сходящейся системы сил
1.Геометрическое – пространственный многоугольник сил должен быть
n
замкнут, т.е. геометрическая сумма сил равна нулю F 0 .
i 1
2. Аналитические – сумма проекций сил на оси координат ox, oy, oz должна
n |
n |
n |
|
быть равна нулю Yi |
0 ; Yi |
0 ; Zi |
0 . |
i 1 |
i 1 |
i 1 |
|
|
|
25 |
|
Аналитические условия равновесия при рассмотрении равновесия пространственной сходящейся системы сил предпочтительней, чем геометрические, т.к. последние требуют построение пространственного многоугольника, что графически не всегда возможно.
1.6. Пара сил. Момент пары
а) |
, б) |
Рисунок 21 – Пара сил (а), вектор момента М пары сил Парой сил называется две равные по величине, противоположно
направленные силы линии действия, которые не совпадают (рисунок 21,а).
Пара сил создаѐт вращательный эффект характеристикой пары является момент пары М. Численно момент пары определяется произведением величины одной из сил пар (F1) на плечо этой пары (d). Под плечом пары понимается кратчайшее расстояние между линиями действия сил. М = ± F1·d, знак момента определяется направлением вращательного эффекта: по часовой стрелке со знаком (–), против (+). Вектор момента пары М составляет угол 90° с плоскостью действия пары и направлен в сторону, откуда вращение, вызываемое парой видно против часовой стрелки (рисунок 21,б). Длина вектора М равна модулю М F1 d F1 d.
Свойства пар сил в плоскости
Действие пары сил не изменяется, если:
1)пары сил перенести в любую часть плоскости действия пары;
2)повернуть линии действия пары в плоскости действия пары на любой
угол;
3)трансформировать пары, т.е. изменить F и d таким образом, чтобы произведение F·d осталось неизменным;
4)заменить действие одной пары системой пар сил, лежащих в той же плоскости, что и исходная, при условии, если алгебраическая сумма моментов
26
n
системы пар сил равна моменту исходной пары, т.е. M M i . Справедливо и
I 1
обратное утверждение систему пар сил можно заменить одной парой при
условии, что |
|
= ; |
|
=1 |
|
5) перенести действие пары сил из одной плоскости в параллельную. |
||
Условия равновесия пар сил в плоскости
Система пар сил в плоскости будет находиться в равновесии, если
алгебраическая сумма моментов этой системы равна нулю т.е. |
|
= 0. Так |
|
=1 |
|
как систему пар можно заменить одной парой (свойство из предыдущего
параграфа), то |
|
= = = 0 равенство нулю момента одной пары |
|
=1 |
|
возможно при F = 0 или d = 0. Если d = 0, то силы пары лежит на одной прямой, т.е. удовлетворяют условию аксиомы равновесия двух сил.
1.7. Момент силы относительно заданного центра
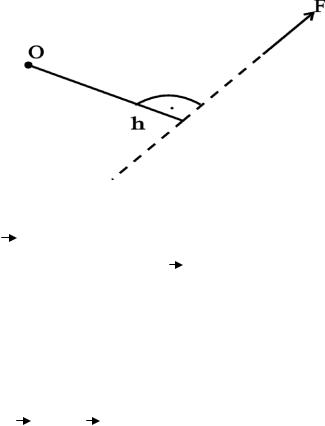
Сила, действуя на твѐрдое тело, может создавать вращательный эффект. Для характеристики вращательного действия силы вводится понятие момента силы относительно заданного центра (точки) или оси. Рассмотрим момент силы относительно заданного центра. Он определяется как произведение величины силы (F) на плечо этой силы h. Под плечом силы понимается кратчайшее расстояние от центра до линии действия силы (рисунок 22).
Рисунок 22 – Плечо силы
Момент силы F относительно заданного центра, например точка О, обозначается М0(F):
М0(F) = ± Fh.
Знак момента: + если, вращение вызываемое силой, направленно против часовой стрелки и –, если по часовой стрелке. На рисунке 22 видно, что момент силы не изменится, если точку приложения силы перемещать вдоль линии действия силы.Две разные по величине силы будут вызывать одинаковый вращательный эффект, если их моменты относительно заданного центра одинаковы, т.е. М0(F1) = М0(F2).
27
Если на твѐрдое тело действует система сил, то момент равнодействующей
n
силы R Fi
i 1
равен алгебраической сумме моментов составляющих, т.е.
|
|
M ( R ) M (F ) . |
|
|
i |
Справедливо и обратное утверждение, т.е. любую силу можно разложить на составляющие, тогда сумма моментов составляющих сил будет равна моменту исходной силы. При решении задач статики данное свойство позволяет упростить определение моментов сил относительно заданного центра.
Определим суммарный момент пары сил относительно заданного центра О (рисунок 23).
Рисунок 23 – Момент пары сил относительно заданного центра Силы 1 и 2 равны по величине и антипараллельны. Моменты этих сил
М0( 1 ) = – h1 ∙ F1; М0( 2 ) = + h2 |
∙ F2 ; суммарный момент М0( 1 ) + М0( 2 ) = |
– h1 ∙ F1 + h2 ∙ F2 = d ∙ F1 = M. |
Следовательно, вне зависимости от выбора |
центра сумма моментов пары сил равна моменту этой пары, т.е. действие пары сил не зависит от выбора центра.
Если центр О лежит на линии действия одной из сил, то получается, это момент пары равен моменту одной силы относительно точке приложения другой силы:
М1( 2 ) = М2( 1 ).
1.8. Приведение плоской произвольной системы сил к заданному центру
Под плоской произвольной системой сил понимается система сил, линии действия которых лежат в одной плоскости и не пересекаются в одной точке.
1. Теорема о параллельном переносе силы. Силу, действующую на твѐрдое тело, можно переносить параллельно самой себя в любую точку этого тела не изменяя еѐ действия, если к действию перенесѐнной силы добавить пару сил с моментом равным моменту перенесѐнной силы относительно точки переноса.
Доказательство. Рассмотрим силу, действующую на твѐрдое тело, приложенную в точке А (рисунок 24). Добавим к действию этой силы две взаимоуравновешенные силы 1 и 2, приложенные в точке (О), куда мы хотим перенести силу .
28
а) |
б) |
Рисунок 24 – Действие силы на твѐрдое тело |
|
Величины уравновешенных сил 1 и 2, равны силе , а линии их действия параллельны силы . Тогда силы 2, и образуют пару сил с момента
М = М0( ) (рисунок 24,б). Момент этой пары изображен на рисунке 24,б в виде дужки со стрелкой. В точке О действует сила 1 = . Таким образом силу мы перенесли в точку О параллельно самой себе, добавив при этом пару сил с моментом М = М0( ). Теорема доказана.
2. Приведение плоской системы сил к заданному центру
Одной из задач статики является упрощение системы сил, действующих на
твѐрдое тело. Рассмотрим произвольную плоскую систему сил, действующих на |
|
тело , i = 1 + n (рисунок 25,а). |
|
|
|
а) |
б) |
Рисунок 25 – Система сил, действующих на тело Перенесѐм все силы параллельно самим себе в точку О. Точку О называют
точкой приведения. Чтобы кинематическое состояние тела не изменилось, к действию перенесѐнных сил добавим систему пар сил с моментами, равными моментом перенесѐнных сил относительно точки переноса (точки приведения) (рисунок 25,б). Систему сил, приложенных в точке О, заменим одной силой,
|
n |
|
|
равной геометрической сумме действующих сил R Fi |
. Эту силу |
R |
|
i 1
называют главным вектором системы. Систему моментов пар сил заменим одной парой сил с моментом, равным алгебраической сумме моментов переносимых
29
n |
n |
|
сил M M i |
M (Fi ) . Этот момент M * называют главным моментом |
|
i 1 |
i 1 |
|
системы. Итак, система сил, лежащая в одной плоскости, приводится к одной
|
|
|
|
|
|
|
M * , |
силе, называемой главным вектором |
R * , |
и паре |
сил |
с |
моментом |
||
называемым главным моментом. |
|
|
|
|
|
|
|
Состоялось |
упрощение системы |
сил: |
систему |
из |
n |
сил заменили |
|
|
|
|
|
|
|
|
|
эквивалентной, |
состоящей из трѐх сил. Отметим, что главный вектор |
R * не |
|||||
зависит от центра приведения, тогда как главный момент M * зависит. Рассмотрим частные случаи приведения:
1) R * = 0; Мо = 0. Если главный вектор системы сил равен нулю и еѐ главный момент относительно заданного центра приведения тоже равен нулю, то силы взаимно уравновешены. Более подробно условия равновесия плоской произвольной системы сил рассмотрим ниже.
2) R * = 0; Мо ≠ 0. Если главный вектор системы сил равен нулю, а главный момент отличен от нуля, то система приводится к паре сил с моментом, не зависящим от точки приведения. В этом случае система сил создаѐт только вращательный эффект.
3) R * ≠ 0; Мо = 0. Если главный вектор отличен от нуля, а главный момент
равен нулю, то система сил приводится к равнодействующей R R* , линия действия которой проходит через точку О.
4) R * ≠ 0; Мо ≠ 0. Если главный вектор и главный момент отличны от нуля, то возможно дальнейшее упрощение (рисунок 26).
а) |
, б) |
, в) |
Рисунок 26 – Приведение сил согласно условия пункта 4
30