
5601
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
Е.А. Мясников
ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические указания к аудиторной контрольной работе
для студентов II (IV) курса заочной формы обучения всех направлений подготовки
Хабаровск 2014
1

УДК 519.2 ББК В
Х 12
Теория вероятности и математическая статистика : метод. указания к аудиторной контрольной работе для студентов II (IV) курса заочной формы обучения всех направлений подготовки / сост. Е. А. Мясников. – Хабаровск : РИЦ ХГАЭП, 2014. – 44 с.
Содержание соответствует государственным образовательным стандартам дисциплины «Теория вероятности и математическая статистика» для бакалаврантов 2-го курса экономических вузов всех направлений подготовки. Учтены все разделы программы. Даны основные понятия, формулы и примеры решения задач. Для самостоятельного изучения.
Рецензент Е. Г. Агапова, к.ф.-м.н., доцент каф. прикладной математики ТОГУ
Утверждено издательско-библиотечным советом академии в качестве методических указаний
Евгений Анатольевич Мясников
ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические указания к аудиторной контрольной работе для студентов II (IV) курса заочной формы обучения всех направлений подготовки
Редактор Г.С. Одинцова
Подписано к печати |
г. Формат 60х84/16. Бумага писчая. |
Печать цифровая. Усл.печ.л. 2,3. |
Уч.-изд. л. 1,7 . Тираж 100 экз. Заказ № . |
680042, г. Хабаровск, ул. Тихоокеанская, 134, РИЦ ХГАЭП
©Мясников Е.А., 2014
©Хабаровская государственная академия экономики и права, 2014
2
Предисловие
Цель указаний – помочь студентам в подготовке к аудиторной контрольной работе (АКР) и к экзамену. При малом числе лекций и практических занятий преподаватель не может разобрать все темы и помочь в возникающих вопросах. Поэтому до сессии желательно самостоятельно получить представление о теории вероятности и попробовать решить стандартные задачи.
В конце указаний предложены примерные варианты АКР и образец оформления работы. Также хорошая практика – изучив решение примеров, взять условие и через некоторое время попытаться решить пример самостоятельно.
Разбиение на параграфы соответствует темам базового курса дисциплины, однако из математической статистики взяты лишь точечные и интервальные оценки параметров и проверка гипотезы о равенстве средних.
На усмотрение преподавателя могут быть включены задания по темам § 6 и 8. Необходимо учесть, что АКР предполагает лишь базовый уровень подготовки. Студенты, претендующие на отличную оценку, должны уметь работать с литературой, в том числе со сборниками задач.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ
§1. Классическое определение вероятности
Втеории вероятности в каждой задаче работают с 3 основными понятиями:
‒испытание ‒ любое действие, результат которого заранее неизвестен;
‒событие ‒ некий факт, возможный при проведении испытания;
‒вероятность ‒ числовая оценка возможности события в испытании.
Пример 1. Двое наугад разделили сумму, не превосходящую 200 руб. ‒ это испытание. Отличие в полученных долях оказалось менее 50 руб. ‒ это событие. Оказывается, так происходит примерно в 7 случаях из 16 ‒ вероятность указанного события в данном испытании составляет 7/16.
События для краткости обозначают буквами А, Б, В и т. д. или же латинскими буквами, а вероятности событий – соответственно P A , P Б , P В .
Если в результате испытания возможны n исходов, ни один из них не предпочтительнее другого и никакие два не могут произойти одновременно, такие ис-
ходы называют элементарными.
3

Пример 2. Новый преподаватель хочет вызвать кого-то к доске. В группе 15 человек. Поскольку он никого не знает, выбор происходит случайным образом, и в результате испытания «вызван студент» возможны 15 элементарных исходов.
Пример 2А. Мы пытаемся найти в шкафу нужную книгу и не знаем, есть ли она там. Возможны 2 исхода ‒ «книга найдена» и «книга не найдена». Они неэлементарны ‒ информации слишком мало, чтобы что-то вычислять.
Определение. Если в результате испытания возможны n элементарных исходов, и в m из этих исходов наступает событие А, то классическая вероятность
события А в данном испытании составляет P A |
m |
. |
|
||
|
n |
|
Пример 3. В лаборатории проверили 8 компьютеров из 20 имеющихся. Какие именно, студент не знает. Каковы шансы, выбирая компьютер случайным обра-
зом, оказаться за уже проверенным? |
|
|||||||
Решение. |
Здесь событие А – «выбрали проверенный компьютер», |
n 20 ‒ |
||||||
общее число компьютеров, |
m 8 |
‒ число проверенных. Исходы элементарны |
||||||
(нет |
никаких |
предпочтений |
для |
выбора какого-либо компьютера). |
Поэтому |
|||
P A |
8 |
0,4 |
‒ примерно в 40% случаев, попадая в такую ситуацию, студент |
|||||
|
|
|||||||
20 |
||||||||
|
|
|
|
|
|
|||
окажется за проверенным компьютером.
Число элементарных исходов находят по формулам комбинаторики.
Число перестановок: n элементов можно расположить по порядку n! способами, где n! 1 2
2 
 n .
n .
Пример 4. У 5 студентов существует 5! 1 2
2  3
3 4
4  5 120 способов организовать очередь для сдачи экзамена.
5 120 способов организовать очередь для сдачи экзамена.
Число сочетаний: m элементов из n имеющихся можно выбрать (без учёта
порядка) C m |
n! |
способами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
n |
m! n m ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 5. 5 команд могут сыграть С 2 |
5! |
1 2 3 4 5 |
4 5 |
10 |
мат- |
|||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
5 |
2! 5 2 ! 1 2 1 2 3 1 2 |
|
|
||||
|
|
|
|
|
|
|||||
чей (без учёта хозяина и гостя), поскольку каждый матч соответствует выбору 2 команд из 5 имеющихся.
Число размещений (без повторений): если при выборе m элементов из n
имеющихся учитывать порядок выбора, получим Am |
|
n! |
способов. |
|
|
|
|
||
|
|
|
||
n |
n |
m ! |
|
|
|
|
|||
4 |
|
|
|
|

Пример 6. 6 туристов выбирают, кому искать дрова, кому собирать грибы,
кому устанавливать палатку. Есть A3 |
|
6! |
120 |
способов такого выбора. |
|
|
|||
|
|
|||
6 |
6 |
3 ! |
|
|
|
|
|
Число размещений с повторениями: имеется n элементов, выбирают m из них, один и тот же элемент можно выбирать несколько раз, и порядок выбора играет роль. Тогда выбрать m элементов из n имеющихся можно nm способами.
Пример 7. Необходимо составить 4-значный шифр из цифр 1, 3 и 7. Очевидно, шифры «1377» и «1737» различны, т.е. порядок важен, и не обойтись без повторения цифр. Таких наборов, от «1111» до «7777», всего 34 81.
Часто встречается следующая
Задача. Среди N объектов имеется S объектов, обладающих неким интересующим нас свойством Х. Случайным образом отобрали M объектов. Какова вероятность, что в точности k из них будут обладать свойством Х.
Решение. Если обозначить событие А – «в точности k объектов среди n взя-
|
C k |
C M k |
|
тых обладают свойством Х», то P A |
S |
N S |
. |
|
|
||
|
|
C M |
|
|
|
N |
|
Пример 8. На занятии 10 студентов, из которых готовы 6. Вызвали 3 человек. Какова вероятность, что в точности 2 из них окажутся готовы к занятию?
Решение. По формуле классической вероятности P A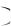 mn , где
mn , где
а) А ‒ интересующее нас событие «из 3 вызванных двое готовы»; б) n ‒ число способов, которыми можно вызвать 3 студентов из 10;
в) m ‒ число способов вызвать 2 готовых и при этом соответственно 1 неготового. Замечаем, что порядок вызова студентов не играет роли.
Найдём знаменатель n |
С 3 |
10! |
|
10! |
|
|
|
1 2 3 10 |
|
|
|
|
8 9 10 |
|
120 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
10 |
|
3! 10 3 ! 3! 7! 1 2 3 1 2 3 |
7 |
|
|
1 2 3 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Значит, 3 студентов из 10 можно вызвать 120 способами (без учёта порядка). |
|
|
|||||||||||||||||||||||||||||||
Находим |
m |
|
|
C 2 |
|
6! |
|
|
|
6! |
|
5 |
6 |
15 |
способов вызвать 2 готовых из 6 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
6 |
|
2! 6 |
2 ! 2!4! |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
возможных. |
Для |
каждой |
такой пары |
есть |
m |
|
C1 |
4! |
|
4! |
|
1 2 |
3 4 |
4 |
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1! 4 1 ! |
1! 3! |
1 1 2 3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
способа добавить кого-то неготового, поскольку всего вызываем 3 человек. |
|
|
|||||||||||||||||||||||||||||||
Тогда P A |
15 4 |
|
0,5 |
‒ вероятность интересовавшего нас события. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
120
Ответ: вероятность составляет 0,5.
5

Пример 9. В коробке 5 яблок и 6 апельсинов. Ребёнку предложили взять 4 фрукта на выбор. Каковы шансы, что он выберет 1 яблоко и 3 апельсина?
Решение. Всего имеется 5 |
6 |
11 фруктов, из которых берём 4. Взять же 4 |
||||||||||||||
фрукта из 11 можно С 4 |
11! |
|
11! |
|
8 9 10 11 |
8 9 10 11 |
|
330 способами. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11 |
4! 11 |
4 ! |
4! 7! |
|
4! |
|
|
|
1 2 3 4 |
|
|
|||||
|
|
|
|
|
|
|
||||||||||
Взять 1 яблоко из 5 имеющихся можно |
С1 |
5! |
5! |
|
5 |
способами, что |
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5 |
1! 5 |
1 ! 1! 4! |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
легко понять по смыслу – сколько яблок, столько и способов взять одно из них.
Взять 3 апельсина из 6 можно С 3 |
6! |
|
6! |
|
4 |
5 6 |
20 |
способами. |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
6 |
3! 6 3 ! |
3! 3! |
1 |
2 3 |
|
|
||
|
|
|
|
|
||||||
Произведение С1 |
С3 |
5 20 100 ‒ это общее число способов взять фрукты в |
||||||||
5 |
6 |
|
|
|
|
|
|
|
|
|
указанном составе: на каждый из 5 способов взять 1 яблоко есть 20 не зависящих от этого способов взять 3 апельсина.
Итак, взять фрукты в указанном составе можно 100 различными способами, а просто взять 4 фрукта из имеющейся коробки ‒ 330 способами. Поэтому вероят-
ность взять 1 яблоко и 3 апельсина равна |
100 |
0,303 . |
|||
330 |
|||||
|
|
|
|
||
Ответ: вероятность составляет |
100 |
, или около 0,303. |
|||
330 |
|||||
|
|
|
|
||
Пример 10. В отделе работают 4 менеджера, 3 инженера, 2 бухгалтера. По
жребию выбрали 3 человек. Каковы шансы, что среди них |
|
|
|
|
|||||
а) все – менеджеры; |
б) все – инженеры; |
|
|
в) нет инженеров; |
|||||
г) у всех разная специальность; |
|
д) у всех одинаковая специальность. |
|||||||
Решение. Всего в отделе работают 9 человек ( 4 3 |
2 |
|
9 ). Для ответа на все |
||||||
вопросы понадобится формула P A |
m |
, где n C 3 |
9! |
|
7 |
8 9 |
84 ‒ число |
||
|
|
|
|
|
|
||||
|
|
n |
9 |
3!6! |
1 |
2 3 |
|
||
|
|
|
|
||||||
способов выбрать 3 человек из 9. Числитель m зависит от конкретного вопроса:
а) m |
C 3 |
|
4 способа выбрать 3 менеджеров из 4 работающих; |
|||
1 |
4 |
|
|
|
|
|
б) m |
C3 |
|
1 способ выбрать 3 инженеров из 3 работающих; |
|||
2 |
3 |
|
|
|
|
|
в) m |
C3 |
3 |
|
C3 |
20 |
способов выбрать 3 человек из 6 «неинженеров» ; |
3 |
9 |
|
6 |
|
|
|
г) m |
C1 |
|
C1 |
C1 |
4 |
3 2 24 способа выбрать 1 менеджера из 4, 1 инженера |
4 |
4 |
|
3 |
2 |
|
|
из 3 и 1 бухгалтера из 2. Числа перемножаем, поскольку на каждый способ выбрать менеджера есть несколько способов выбрать инженера, и т. д.;
д) m5 С43 С33 С23 4 1 0 5 способов, где 0 ‒ число способов выбрать 3
бухгалтеров из 2 работающих (очевидно, это невозможно, а при попытке вычис-
6

ления появится величина  1 !, не имеющая смысла. Числа складываем, поскольку можем выбрать или менеджеров, или инженеров, или бухгалтеров. Подробнее, в каких случаях числа умножают, а в каких складывают, объяснено в §
1 !, не имеющая смысла. Числа складываем, поскольку можем выбрать или менеджеров, или инженеров, или бухгалтеров. Подробнее, в каких случаях числа умножают, а в каких складывают, объяснено в §
2.
Теперь находим сами вероятности:
а) P A |
|
4 |
|
|
|
1 |
|
; |
|
|
|
|
б) P A |
|
1 |
|
; |
в) P A |
20 |
|
5 |
; |
|||
1 |
84 |
|
|
|
21 |
|
|
|
2 |
84 |
|
|
3 |
84 |
21 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
г) P A |
|
24 |
|
2 |
; |
|
|
|
|
д) P A |
5 |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
|
84 |
|
|
|
7 |
|
|
|
|
|
|
5 |
84 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
1 |
|
; |
1 |
|
; |
5 |
; |
2 |
; |
5 |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
21 |
84 |
21 |
|
7 |
|
84 |
|
|
|
|
|
|
|
|
|
|
||||||||
§ 2. Алгебра вероятностей
Определение. События А и Б называются несовместными, если наступление одного ведёт к невозможности (в том же испытании) другого.
Пример 1. Пусть событие А означает, что студент получил на экзамене оценку «отлично», а событие «Б» ‒ что он же получил оценку «хорошо». События А и Б несовместны: получить 2 оценки за один и тот же экзамен невозможно.
Пример 1А. Если событие А означает, что студент сдал математику, а событие Б – что в другой день он сдал историю, то эти события совместны.
Определение. Сумма событий А и Б – это событие (обозначаемое А Б ), при котором наступает или А, или Б, или оба события.
Теорема. Вероятность суммы двух несовместных событий А и Б равна сумме вероятностей каждого из них: P А Б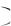 P А
P А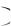 P Б .
P Б .
Пример 2. Около 20% времени на АЗС нет машин, около 30% – находится только одна машина. Какова доля времени, когда на АЗС не более 1 машины?
Решение. Если событие А – «На АЗС нет машин» и событие Б – «на АЗС 1 машина», то по условию P А 0,2 и P Б
0,2 и P Б 0,3, и нас интересует событие А Б . Очевидно, А и Б несовместны, поэтому P А Б
0,3, и нас интересует событие А Б . Очевидно, А и Б несовместны, поэтому P А Б Р А
Р А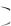 Р Б
Р Б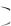 0,2 0,3 0,5.
0,2 0,3 0,5.
Ответ: 50% всего времени на АЗС находится не более 1 машины.
Определение. События А и Б независимы, если наступление одного никак не влияет на возможность наступления другого.
7
Так, в примере 1А события А и Б не только совместны, но и независимы (ничто не мешает удачно сдать историю, если не сдана математика). Если же преподаватель вопреки правилам начнёт смотреть, как студент сдал предыдущий экзамен, и учитывать это, события станут зависимы.
Определение. Произведение событий А и Б ‒ это событие (обозначаемое А Б или АБ ), при котором происходят оба события: и А, и Б.
Б или АБ ), при котором происходят оба события: и А, и Б.
Впримере 1 произведение АБ означает, что студент сдал экзамен на отлично
ипри этом на хорошо (что невозможно, поэтому Р АБ 0 ). В примере 1А – что
0 ). В примере 1А – что
студент сдал и математику, и историю, что вполне возможно.
Теорема. Вероятность произведения двух независимых событий равна произведению их вероятностей: Р А Б
Б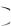 Р А
Р А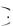 Р Б .
Р Б .
Пример 3. Около 70% студентов сдают математику (вовремя), около 80% ‒ историю. Каковы шансы для отдельно взятого студента вовремя сдать и математику, и историю?
Решение. Пусть А означает, что студент сдал математику, Б – что он же сдал историю. По условию Р А 0,7 и Р Б
0,7 и Р Б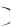 0,8. Тогда Р АБ
0,8. Тогда Р АБ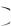 0,7
0,7 0,8 0,56 .
0,8 0,56 .
Ответ: 0,56, т.е. примерно 56% студентов вовремя сдают обе дисциплины.
События зависимы, если наступление одного меняет вероятность другого.
Теорема. Если событие Б зависит от события А, то вероятность их произведения Р АБ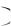 Р А РА Б , где РА Б
Р А РА Б , где РА Б 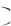 ‒ вероятность события Б при условии, что событие А произошло.
‒ вероятность события Б при условии, что событие А произошло.
Пример 4. Среди 60 телевизоров есть 4 неисправных. Каковы шансы, проверив 2 телевизора, обнаружить 2 неисправных?
Решение. Можно найти С42 / С602 , но быстрее сделать так: пусть А означает,
что 1-й проверенный телевизор оказался неисправен, а Б – что после этого 2-й телевизор также оказался неисправен. По формуле классической вероятности
Р А |
4 |
|
1 |
|
‒ отношение числа неисправных телевизоров к общему числу. |
|
60 |
15 |
|||||
|
|
|||||
Проверенный неисправный телевизор удаляется, и телевизоров остаётся 59,
из которых неисправных уже не 4, а 3. Но тогда РА Б  593 , где индекс А указы-
593 , где индекс А указы-
8
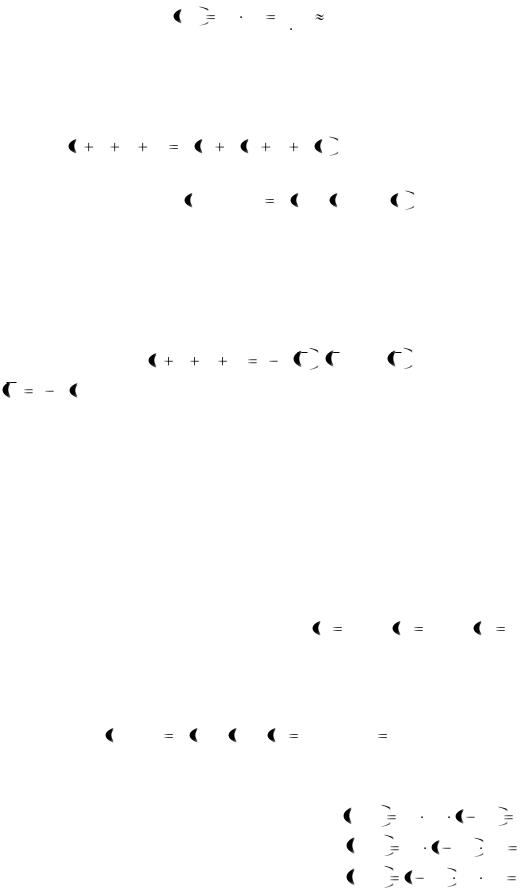
вает, что 1-й телевизор оказался неисправен. По формуле вероятности произве-
дения зависимых событий |
Р АБ |
4 |
3 |
1 |
0,003 39 . |
|||
|
|
|
|
|
||||
60 |
59 |
5 59 |
||||||
|
|
|
||||||
Ответ: вероятность составляет 1/ 295 , или около 0,339%.
Для трёх и более событий действуют те же правила:
а) вероятность суммы несовместных событий равна сумме вероятностей каж-
дого из них: Р А Б В Р А
Р А Р Б
Р Б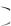 Р В ;
Р В ;
б) вероятность произведения независимых событий равна произведению вероятностей каждого из них: Р А Б
Б 
 В
В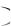 Р А
Р А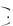 Р Б
Р Б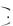
 Р В ;
Р В ;
в) вероятность произведения зависимых событий равна произведению вероятностей каждого из этих событий при условии, что все, от которых оно зависит, произошли (см. пример 6).
Вероятность суммы нескольких совместных событий (она же – вероятность хотя бы одного события) удобно находить по формуле
Р А Б В 1 Р А Р Б
1 Р А Р Б 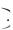
 Р В ,
Р В ,
где Р А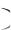 1 Р А
1 Р А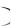 ‒ вероятность того, что А не наступило, и т.д.
‒ вероятность того, что А не наступило, и т.д.
Во многих задачах интересующее нас событие распадается на сумму несовместных событий, каждое из которых, в свою очередь – произведение ещё более мелких событий (возможно, зависимых).
Пример 5. Три друга собираются в поход и оценивают свои возможности (шансы, что удастся пойти) в 80, 70 и 60%. Что вероятнее: что в поход пойдут все или в точности двое (неважно кто)?
Решение. Обозначим события «1-й пошёл», «2-й пошёл» и «3-й пошёл» соответственно как А, В и С. По условию задачи P A 0,8, P B
0,8, P B 0,7, P C
0,7, P C 0,6 .
0,6 .
Событие «все три друга отправились в поход» ‒ это произведение событий А, В и С. Поскольку нет указаний, что возможности каждого как-то зависят от остальных, считаем события А, В, С независимыми. Тогда
P A B
B  C
C P A
P A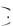 P B
P B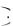 P C
P C 0,8
0,8 0,7
0,7 0,6 0,336 .
0,6 0,336 .
Событие «в точности двое отправились в поход» (обозначим его буквой Е)
сложнее и распадается на сумму трёх несовместных событий: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
ABC |
‒ 1-й и 2-й пошли, а 3-й остался дома, P ABC |
0,8 0,7 |
1 |
0,6 |
0,224 ; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) |
|
AB |
С ‒ 1-й и 3-й пошли, а 2-й остался дома, P AB |
C |
0,8 |
1 |
0,7 |
0,6 |
0,144 ; |
|||||||||
в) |
|
|
BC |
|
|
|
0,084 , |
|||||||||||
|
A |
BC ‒ 2-й и 3-й пошли, а 1-й остался дома, P |
A |
1 |
0,8 |
0,7 0,6 |
||||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
||||||

поэтому P E 0,224 0,144 0,084 0,452 . Итак, с вероятностью 0,336 в поход пойдут все, а с вероятностью 0,452 пойдут двое и кто-то останется дома.
0,224 0,144 0,084 0,452 . Итак, с вероятностью 0,336 в поход пойдут все, а с вероятностью 0,452 пойдут двое и кто-то останется дома.
Ответ: более вероятно, что пойдут двое, а не все.
Пример 6. Из 9 кандидатов на вакантную должность подходят четверо. Каковы шансы, что подходящий человек будет определён с 1-й попытки? со 2-й? с 3-й попытки? Не позже, чем с 3-й попытки?
Решение. По смыслу неподходящий кандидат уходит, и шансы закрыть вакансию при проверке следующего меняются (повышаются).
Вероятность, что при просмотре кандидатов в случайном порядке первый же из них нас устроит (обозначим такое событие буквой А) ‒ это доля подходящих
кандидатов в общем числе: P A |
4 |
0,444 . |
|
|
|||
9 |
|||
|
|
Событие Б ‒ «кандидат подошёл со 2-й попытки» будет произведением 2 событий: Б Б1  Б2 , где Б1 ‒ 1-й кандидат нас не устроил (иначе проверять 2-го незачем); Б2 ‒ 2-й кандидат нам подошёл.
Б2 , где Б1 ‒ 1-й кандидат нас не устроил (иначе проверять 2-го незачем); Б2 ‒ 2-й кандидат нам подошёл.
Всего нас не устраивают |
9 4 5 человек, поэтому P Б |
5 |
. После этого |
|
|||
|
1 |
9 |
|
|
|
|
остаются 8 кандидатов, и среди них 4 подходящих. Значит, РБ1 Б2 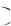 84 . По фор-
84 . По фор-
муле вероятности произведения зависимых событий
Р Б Р Б1 РБ |
Б2 |
5 |
4 |
5 |
0,278 . |
|||
|
|
|
|
|
||||
9 |
8 |
18 |
||||||
1 |
|
|
||||||
|
|
|
|
|
|
|
||
Событие В ‒ «только 3-й кандидат нас устроил». Оно превращается в произведение 3 событий: В1 ‒ 1-й кандидат не устроил; В2 ‒ 2-й кандидат не устроил;
В3 ‒ 3-й кандидат подошёл. Поскольку состав всё время менялся,
РВ1  95 ‒ из 9 человек не подходили 5;
95 ‒ из 9 человек не подходили 5;
Р |
|
|
В |
4 |
‒ из 8 оставшихся не подходили уже 4 (а 1 ушёл); |
|
В |
|
|
||||
|
|
2 |
8 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
В |
|
4 |
‒ из 7 оставшихся подходили по-прежнему 4, как и в самом |
В В |
|
|
||||
|
3 |
|
7 |
|
||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||
начале конкурса. По формуле вероятности произведения зависимых событий
Р В1 РВ В2 |
РВ В |
В3 |
5 |
4 |
4 |
10 |
0,159 . |
|||||
|
|
|
|
|
|
|
||||||
9 |
8 |
7 |
63 |
|||||||||
1 |
1 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
Вероятность, что вакансия закроется не позже, чем с 3-й попытки, можно найти 2 способами:
10
