
- •Кафедра математики и математических методов в экономике
- •Рекомендовано Дальневосточным региональным учебно-методическим центром (ДВ РУМЦ) в качестве учебного пособия для студентов экономических специальностей вузов региона
- •Хабаровск 2007
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………..………………………..102
- •ПРИЛОЖЕНИЕ..……………………..…………...…………………………103
- •1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- •1.1. Комбинаторика
- •Таблица 1
- •Формулы вероятностей появлений события в схеме Бернулли
- •число_успехов – это количество испытаний, в которых появилось интересующее нас событие;
- •Дано: n=8; p=0,3; q=1– p =0,7; а) m≤3; б) m=3.
- •Таблица 3
- •Общие сведения о математическом ожидании и дисперсии ДСВ
- •Ясеновская Инна Витальевна
- •Саяпина Юлия Геннадьевна
- •Практикум

Таблица 3
Общие сведения о математическом ожидании и дисперсии ДСВ
Числовая |
Математическое ожидание |
Дисперсия |
|
||||||
характеристика |
|
||||||||
|
|
|
|
|
|
|
|
||
Обозначение |
|
М(Х) или mx |
D(X) или Dx |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
D( X ) |
M ( X mx ) |
2 |
||
|
|
M ( X ) |
xi pi |
|
|||||
Определяющие |
|
|
|
||||||
|
|
|
или |
|
|||||
формулы |
|
i |
1 |
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
D( X ) |
M ( X 2 ) mx2 |
||||
|
|
|
|
|
|||||
|
|
|
|
|
рассеивание значений СВ |
||||
Характеризует |
|
среднее значение СВ |
относительно среднего значения |
||||||
|
|
|
|
|
|
||||
- в физическом |
центр тяжести многоугольника |
разброс распределения |
|||||||
смысле |
относительно центра тяжести |
||||||||
|
распределения |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
- вгеометрическом |
|
|
|
|
растяжение или сжатие по оси |
||||
смысле |
|
смещение по оси ОХ |
|
OX |
|
||||
|
|
|
|
|
|
|
|||
|
1. М(С) = С, |
С = const. |
1. D(С) = 0, |
С = const. |
|||||
|
|
|
|
|
|||||
|
|
2. М(С∙X) = С∙M(X). |
2. D(С∙X) = С2 ∙D(X). |
||||||
|
3. M ( X1 X 2 |
|
X n ) |
3. D( X1 |
X 2 |
X n ) |
|||
|
M ( X1 ) M ( X 2 ) M ( X n ) . |
D( X1 ) D( X 2 ) D( X n ) , |
|||||||
Свойства |
4. |
M (X1 X 2 X n ) |
если X1 ,..., X n - независимые |
||||||
|
M (X1 ) M (X 2 ) M (X n ) , |
случайные величины. |
|||||||
|
если |
X1 ,..., X n |
– независимые |
4. D( X Y ) |
D( X ) D(Y ) |
||||
|
M 2 ( X ) D(Y ) M 2 (Y ) D( X ) , |
||||||||
|
|
случайные величины. |
|||||||
|
|
если X и Y - независимые |
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
случайные величины. |
||||
|
|
|
|
|
|
|
|
|
|
В MS Excel для вычисления числовых характеристик дискретных случайных величин могут быть использованы функции:
 для вычисления математического ожидания можно использовать встроенную функцию СУММПРОИЗВ. Синтаксис функции
для вычисления математического ожидания можно использовать встроенную функцию СУММПРОИЗВ. Синтаксис функции
СУММПРОИЗВ (Массив1;Массив2;…), где Массив1, Массив2,
… от 2 до 30 массивов чьи компоненты нужно перемножить, а затем сложить произведения;
 для вычисления среднего квадратического отклонения используется функция КОРЕНЬ. Синтаксис функции КОРЕНЬ (Число).
для вычисления среднего квадратического отклонения используется функция КОРЕНЬ. Синтаксис функции КОРЕНЬ (Число).
23

Пример
Каждый день местная газета получает заказы на новые рекламные объявления, которые будут напечатаны на следующий день. Число рекламных объявлений в газете зависит от многих факторов: дня недели, сезона, общего состояния экономики и т.д. Определить числовые характеристики случайной величины Х − числа новых рекламных объявлений, если она имеет следующий закон распределения
Хi |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
Рi |
0,02 |
0,15 |
0,34 |
0,36 |
0,13 |
|
|
|
|
|
|
Решение
1.Построим в диапазоне А1:F2 заданную таблицу распределения.
2.По заданной таблице распределения найдём математическое ожидание М(Х) = mx. Для этого необходимо:
установить курсор в ячейку А4, внести текст mx= ;
установить курсор в ячейку В4, обратиться к Мастеру функций и найти функцию СУММПРОИЗВ ОК;
воткрывшемся диалоговом окне Аргументы функции
установить курсор в поле Массив1 и выделить мышкой диапазон В1:F1. Затем установить курсор в поле Массив2 и выделить диапазон В2:F2 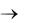 ОК. Полученный результат соответствует вычисленному по формуле (1).
ОК. Полученный результат соответствует вычисленному по формуле (1).
3. Для вычисления дисперсии составим новую таблицу, вычислив в первой строке значения (xi – mx)2 . Для этого:
 скопировать в диапазон А6:F7 заданную таблицу распределения, очистить первую строку и внести в ячейку А6 текст (xi – mx)2;
скопировать в диапазон А6:F7 заданную таблицу распределения, очистить первую строку и внести в ячейку А6 текст (xi – mx)2;
активизировать ячейку В6 и создать формулу для вычисления =(x1 – mx)2. При создании формулы ссылаться на ячейки, в которых находятся значения х1=0 (ячейка В1) и mx (ячейка В4), при этом ссылка на ячейку В4 должна быть абсолютной;
24

скопировать полученную формулу (при помощи маркера заполнения) в диапазон С6:F6;
по вновь полученной таблице найти значение дисперсии. Для этого установить курсор в ячейку А9 и внести текст D(X)= ;
установить курсор в ячейку В9, обратиться к Мастеру функций и найти функцию СУММПРОИЗВ ОК;
воткрывшемся диалоговом окне Аргументы функции
установить курсор в поле Массив1 и выделить мышкой диапазон В6:F6. Затем установить курсор в поле Массив2 и выделить диапазон В7:F7 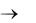 ОК. Полученный результат соответствует вычисленному по формуле (2).
ОК. Полученный результат соответствует вычисленному по формуле (2).
4. Для вычисления среднего квадратического отклонения используем функцию КОРЕНЬ. Для этого:
установить курсор в ячейку А11 и ввести текст σх=;
установить курсор в ячейку В11, обратиться к Мастеру функций и найти функцию КОРЕНЬ ОК;
в открывшемся диалоговом окне установить курсор в поле Число и щелкнуть мышкой по ячейке В9 (ячейка с вычисленным ранее значением D(X)). Полученный результат соответствует вычисленному по формуле (3).
5. Сравните полученный результат работы с образцом:
25
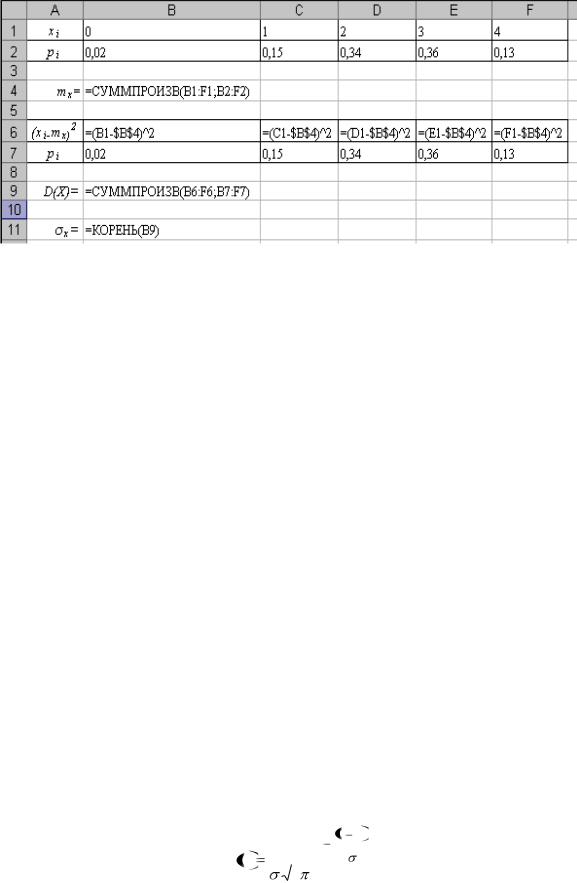
Формульный вариант:
УПРАЖНЕНИЯ 1. Найти числовые характеристики случайной величины Х, заданной
законом распределения:
Хi |
0 |
1 |
2 |
3 |
|
|
|
|
|
Рi |
0,343 |
0,441 |
0,189 |
0,027 |
|
|
|
|
|
2. Дискретная случайная величина Х – число изделий первого сорта среди пяти отобранных задаётся следующим законом распределения:
Хi |
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
Рi |
|
0,00032 |
0,0064 |
0,0512 |
0,2048 |
0,4096 |
0,32768 |
|
|
|
|
|
|
|
|
|
|
Найти |
математическое |
ожидание |
и среднее квадратическое |
|||||
отклонение случайной величины Х.
1.5. Нормальный закон распределения
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
|
|
|
|
|
x |
a 2 |
|
|
f x |
1 |
|
e 2 |
2 . |
||||
|
|
|
||||||
2 |
||||||||
|
|
|
|
|
|
|||
26
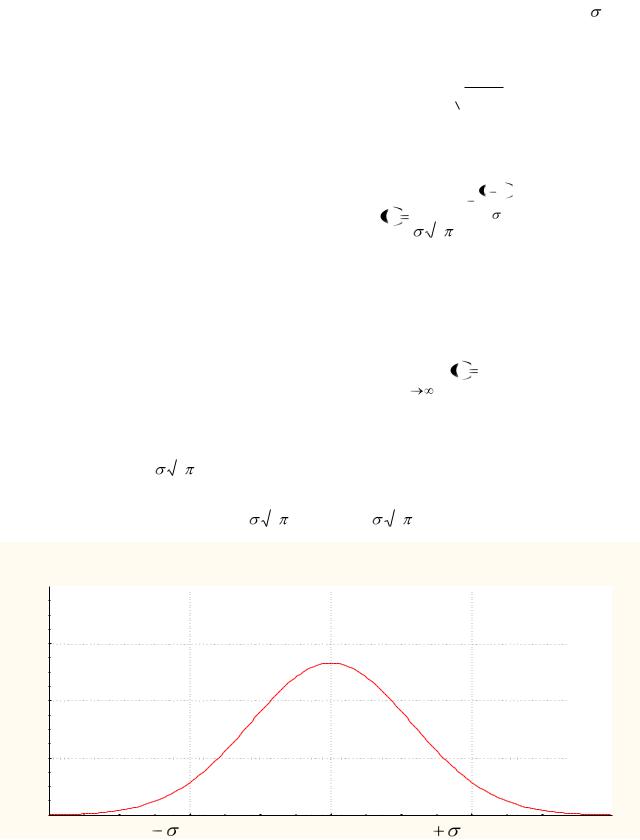
Данное распределение определяется двумя параметрами: а и , достаточно знать эти параметры, чтобы задать нормальное распределение.
Параметры а и σ имеют следующий вероятностный смысл:
а = М(Х), σ 2= D(Х), σ = 
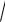 D(x) .
D(x) .
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
|
|
|
|
|
x |
a 2 |
|
|
Исследуем и построим график функции f x |
1 |
|
e 2 |
2 (рис. 2). |
||||
|
|
|
||||||
2 |
||||||||
|
|
|
|
|
|
|||
1.Функция ƒ(х) определена на всей оси Х.
2.При любых значениях Х функция принимает положительные значения, т.е. лежит выше оси ОХ.
3.Предел функции при неограниченном возрастании x (по
|
абсолютной |
|
|
величине) |
|
равен нулю: |
|
|
lim f x 0 , т.е. ось Оx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
служит горизонтальной асимптотой графика. |
||||||||||||||||||
4. |
Точка (а, |
|
1 |
|
|
) – точка max. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. |
Точки перегиба (а-σ, |
|
1 |
|
) и (а+σ, |
|
1 |
|
|
). |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 e |
|
|
2 e |
||||||||||||||
Probability Density Function
f(x) |
|
|
y=normal(x;0;1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,60 |
|
|
|
|
|
|
|
|
0,45 |
|
|
|
|
|
|
|
|
0,30 |
|
|
|
|
|
|
|
|
0,15 |
|
|
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
|
|
-3,50 |
a |
-1,75 |
a |
0,00 |
a |
1,75 |
X |
3,50 |
|
|
|
|
|
||||
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
27 |
|
|
|
|

|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
Если функция Лапласа задается формулой |
Ф(х) = |
|
|
|
e t |
/ 2 dt , то |
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
для нормально распределённой случайной величины |
|
|
|
|
|
|
|||||||||
Р ( < Х < ) = Ф |
a |
- Ф |
|
|
|
a |
. |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р( |
Х а |
< ) = 2Ф |
|
|
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
В Excel для вычисления значений нормального распределения используются функции НОРМРАСП и НОРМСТРАСП.
Функция НОРМРАСП вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения. Синтаксис этой функции имеет вид — НОРМРАСП (х;
среднее; стандартное_откл; интегральная),
где х — значение, для которого строится распределение; среднее — среднее арифметическое распределения;
стандартное_откл — стандартное отклонение распределения; интегральная — значение, определяющее форму функции.
Если интегральная имеет значение истина, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ложь, то вычисляет значение функция плотности распределения.
Если среднее = 0 и стандартное_откл = 1, то функция НОРМРАСП
возвращает стандартное нормальное распределение, то есть
НОРМСТРАСП.
Пример
Построить график нормальной функции плотности вероятности f(x)
при М(Х) = 24,3 и ( X ) = 1,5.
28
Решение
1.В ячейку А1 вводим символ случайной величины Х, а в ячейку В1 — символ функции плотности вероятности — f(x).
2.Вычисляем диапазон М(Х)±3σ — от 19,8 до 28,8. Вводим в диапазон А2:А20 значения Х от 19,8 до 28,8 с шагом 0,5. Для этого в ячейку А2 вводим левую границу диапазона (19,8), а в ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:АЗ. Затем за правый нижний угол протягиваем мышью до ячейки А20 (при нажатой левой кнопке).
3.Устанавливаем табличный курсор в ячейку В2 и для получения значения вероятности воспользуемся специальной функцией — нажимаем на панели инструментов кнопку Вставка функции (fx).
4.В появившемся диалоговом окне Мастер функций-шаг 1 из 2 в поле Категория указаны виды функций. Выбираем Статистическая. В поле Функция выбираем функцию НОРМРАСП. Нажимаем на ОК.
5.Появляется диалоговое окно НОРМРАСП. В рабочее поле х вводим значение х, для которого строится распределение (в примере адрес ячейки А2 щелчком мыши на этой ячейке). В рабочее поле Среднее
вводим с клавиатуры значение математического ожидания М(Х) (в примере — 24,3). В рабочее поле Стандартное_откл вводим с клавиатуры значение среднеквадратического отклонения σ (в примере — 1,5). В рабочее поле Интегральный вводим с клавиатуры вид функции распределения — интегральная или весовая (в примере — 0). Нажимаем па кнопку ОК.
6.В ячейке В2 появляется вероятности р = 0,002955.
7.Указателем мыши за правый нижний угол табличного курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В20 копируем функцию НОРМРАСП в диапазон ВЗ:В20.
8.По полученным данным строим искомую диаграмму нормальной функции распределения. Щелчком указателя мыши на кнопке на панели инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне выбираем тип диаграммы График, вид — левый
29
верхний. После нажатия кнопки Далее указываем диапазон данных
— В2:В20 (с помощью мыши). Проверяем положение переключателя Ряды: в столбцах. Выбираем вкладку Ряд и с помощью мыши вводим диапазон подписей оси Х: А2:А20. Нажав на кнопку Далее, вводим названия осей X и У: х и f(х), соответственно. Нажимаем на кнопку Готово.
УПРАЖНЕНИЯ 1. Построить график нормальной функции плотности вероятности
f(x) при М(Х) = 10 и ( X ) = 2.
2.Автомобильный завод выпускает в производство новый двигатель. Конструкторы двигателя считают, что средняя длина пробега для автомобиля с новым двигателем составляет 160 тыс. км. Со стандартным отклонением 30 тыс. км. Чему равна вероятность того, что до первого ремонта число километров пробега автомобиля будет находиться в пределах от 100 тыс. км. до 180 тыс. км? Изобразить графически.
30

2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
2.1. Первичная обработка статистических данных
Пусть из генеральной совокупности извлечена выборка, причем x1
наблюдалось n1 раз, x2 n2 раз, xk nk раз и ni n  объём выборки.
объём выборки.
Наблюдаемые значения xi называют вариантами, а последовательность
вариант, |
записанных в возрастающем порядке, вариационным рядом. |
||
Числа ni |
наблюдений называют частотами, а их отношения к объёму |
||
выборки |
ni |
wi |
относительными частотами. |
n |
|||
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Различают дискретные и интервальные статистические распределения.
Статистическое распределение называется дискретным, если значения признака отличаются друг от друга не менее чем на некоторую постоянную величину.
xi |
x1 |
|
x2 |
|
xk |
|
|
|
|
|
|
ni |
n1 |
|
n2 |
|
nk |
|
|
|
|
|
|
wi |
w1 |
|
w2 |
|
wk |
|
|
|
|
|
|
|
k |
|
k |
|
|
|
ni |
n; |
wi |
1. |
|
|
i 1 |
|
i 1 |
|
|
Для графического представления дискретного распределения используют полигон частот (полигон относительных частот).
Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами x1; n1 , x2 ; n2 , , xk ; nk . Для построения полигона на оси абсцисс откладывают варианты xi , а на оси ординат – соответствующие им частоты ni . Точки xi ; ni  соединяют отрезками прямых и получают полигон частот (рис. 3).
соединяют отрезками прямых и получают полигон частот (рис. 3).
31

ni |
|
|
ni |
|
|
n2 |
|
|
n1 |
|
|
nk |
|
|
0 x1 x2 |
xi xk |
xi |
|
Рис. 3 |
|
В случае непрерывных |
случайных |
величин рассматривают |
интервальное статистическое распределение выборки. Оно оформляется в виде следующей таблицы:
|
|
|
(xi ; xi 1) |
(x1; x2 ) |
(x2 ; x3 ) |
|
|
(xk 1; xk ) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
|
n1 |
n2 |
|
|
|
nk |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wi |
|
w1 |
w2 |
|
|
|
wk |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
ni n; |
|
wi |
1. |
|
|
|
|
|
|
|
|
|
i 1 |
i |
1 |
|
|
|
|
|
Разница между двумя соседними вариантами называется шагом |
|||||||||||||
интервала h |
xi |
xi |
1. От интервального распределения можно перейти к |
||||||||||
дискретному, взяв на каждом интервале |
xi ; xi |
1 за отдельное значение xi* |
|||||||||||
* |
xi |
xi |
1 |
|
|
|
|
|
|
|
|
|
|
величину xi |
|
|
|
|
, являющуюся серединой этого интервала. |
||||||||
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графической характеристикой интервальных распределений является гистограмма частот (гистограмма относительных частот).
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы
длиною h , а высоты равны отношению |
ni |
(плотность частоты) (рис. 4). |
|
h |
|||
|
|
32
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси
абсцисс, на расстоянии nhi .
ni
h
n2
h n1
h
0 |
x1 |
x2 x3 xk 1 xk xi xi 1 |
Рис. 4
В Excel категория функций Статистические содержит наибольшее количество встроенных функций. Для представления статистического распределения выборки используются специальная функция ЧАСТОТА.
Функция ЧАСТОТА вычисляет абсолютную частоту появления значений в некотором массиве данных. Функция задается в качестве формулы массива. Синтаксис этой функции выглядит так: ЧАСТОТА
(массив_данных; массив_интервалов). Здесь:
 массив_данных – это массив или ссылка на множество данных, для которых вычисляются частоты;
массив_данных – это массив или ссылка на множество данных, для которых вычисляются частоты;
 массив_интервалов – задает диапазон или ссылку на множество интервалов, в которые группируются значения аргумента
массив_интервалов – задает диапазон или ссылку на множество интервалов, в которые группируются значения аргумента
массив_данных.
Отметим, что количество элементов в возвращаемом массиве на единицу больше числа элементов в массив_интервалов. Дополнительный элемент в возвращаемом массиве содержит количество значений, больших, чем максимальное значение в интервалах.
33

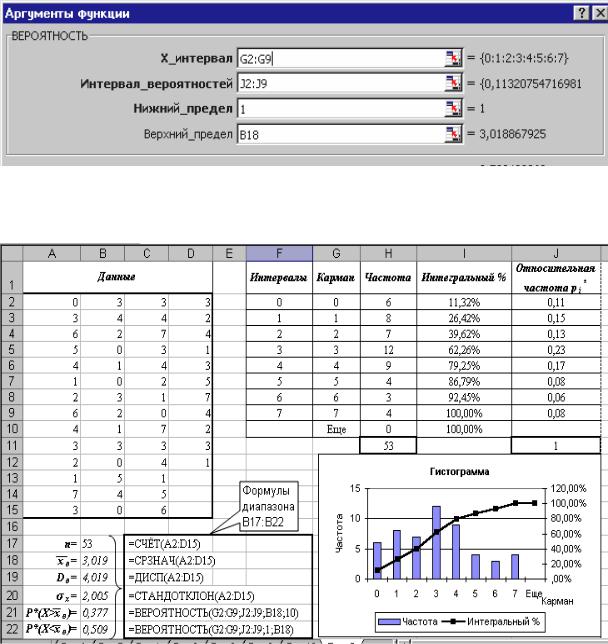
Пример
Из группы второкурсников (100 человек) факультета случайным образом отобрано 25. По журналу успеваемости в течение семестра собраны статистические данные о количестве пропущенных занятий по дисциплине «Теория вероятностей и математическая статистика» каждым из попавших в выборку 25 студентов:
2; 5; 0; 1; 6; 3; 0; 1; 5; 4; 0; 3; 3; 2; 1; 4; 0; 0; 2; 3; 6; 0; 3; 0; 1
Т.е. первый по списку студент пропустил 2 занятия; второй по списку студент пропустил 5 занятий и т.д.
Провести первичную обработку статистических данных о пропусках занятий студентами второго курса факультета:
1.Составить дискретное статистическое распределение выборки.
2.Составить распределение относительных частот.
3.Определить, какая часть студентов факультета пропустила в семестре а) не более трех занятий, б) более трех занятий.
4.Построить полигон частот.
Решение
1. Заносим статистические данные на лист Excel. Для этого:
установим курсор в ячейку В1 и введём текст Данные;
в диапазон В2:В26 введём данные о пропусках:
2; 5; 0; 1; 6; 3; 0; 1; 5; 4; 0; 3; 3; 2; 1; 4; 0; 0; 2; 3; 6; 0; 3; 0; 1.
2. Представим выборочные данные в виде вариационного ряда, для этого ранжируем их в порядке возрастания:
установим курсор в ячейку D1 и введем текст Варианта;
 в диапазон D2:D7 запишем в порядке возрастания значения вариант наблюдаемых в выборке. Для упрощения задачи отбора значений вариант отсортируем диапазон данных В2:В26 по возрастанию (значения, наблюдаемые в выборке – 0; 1; 2; 3; 4; 5; 6).
в диапазон D2:D7 запишем в порядке возрастания значения вариант наблюдаемых в выборке. Для упрощения задачи отбора значений вариант отсортируем диапазон данных В2:В26 по возрастанию (значения, наблюдаемые в выборке – 0; 1; 2; 3; 4; 5; 6).
3.Находим абсолютные частоты, то есть подсчитываем, сколько
34
раз встречается каждое из значений, и проверяем условие нормировки. Для этого:
 установим курсор в ячейку Е1 и введем текст Абсолютная частота ni;
установим курсор в ячейку Е1 и введем текст Абсолютная частота ni;
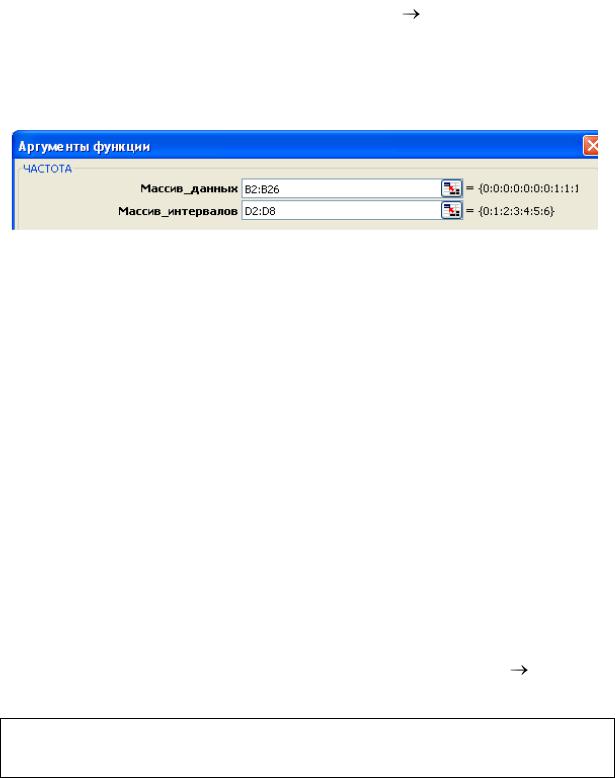
 выделим диапазон ячеек Е2:Е8 (начиная с ячейки Е2), вызываем Мастера функций, находим функцию ЧАСТОТА ОК;
выделим диапазон ячеек Е2:Е8 (начиная с ячейки Е2), вызываем Мастера функций, находим функцию ЧАСТОТА ОК;
 заполним поля диалогового окна Аргументы функции и нажмём сочетание клавиш Ctrl + Shift + Enter: Диапазон Е2:Е8 заполнится значениями абсолютных частот;
заполним поля диалогового окна Аргументы функции и нажмём сочетание клавиш Ctrl + Shift + Enter: Диапазон Е2:Е8 заполнится значениями абсолютных частот;
 для проверки условия нормировки установим курсор в ячейку E10 и выполним суммирование диапазона Е2:Е8. Сумма абсолютных частот должна быть равна объёму выборки n (в нашем случае n=25).
для проверки условия нормировки установим курсор в ячейку E10 и выполним суммирование диапазона Е2:Е8. Сумма абсолютных частот должна быть равна объёму выборки n (в нашем случае n=25).
4. Находим относительные частоты и проверяем условие нормировки. Для этого:
 установим курсор в ячейку F1 и введем текст Относительная частота p*i;
установим курсор в ячейку F1 и введем текст Относительная частота p*i;
 для вычисления относительных частот создадим формулу массива. Для этого:
для вычисления относительных частот создадим формулу массива. Для этого:
 выделим диапазон F2:F8;
выделим диапазон F2:F8;
 нажмём кнопку равно (=);
нажмём кнопку равно (=);
 выделим диапазон Е2:Е8;
выделим диапазон Е2:Е8;
 нажмём на кнопку деление (/);
нажмём на кнопку деление (/);
 обратимся к Мастеру функций и найдем функцию СЧЕТ ОК;
обратимся к Мастеру функций и найдем функцию СЧЕТ ОК;
Функция СЧЁТ используется для подсчёта значений в заданном диапазоне. Синтаксис функции – СЧЁТ(Диапазон);
35

 в открывшемся диалоговом окне Аргументы функции установим курсор в поле Значение1 и выделим мышкой диапазон данных В2:В26 нажмём сочетание клавиш Ctrl + Shift + Enter; диапазон F2:F8 заполнится значениями относительных частот;
в открывшемся диалоговом окне Аргументы функции установим курсор в поле Значение1 и выделим мышкой диапазон данных В2:В26 нажмём сочетание клавиш Ctrl + Shift + Enter; диапазон F2:F8 заполнится значениями относительных частот;
 для проверки условия нормировки, установим курсор в ячейку F10 и выполним суммирование диапазона относительных частот (F2:F8). Сумма частот диапазона должна быть равна 1.
для проверки условия нормировки, установим курсор в ячейку F10 и выполним суммирование диапазона относительных частот (F2:F8). Сумма частот диапазона должна быть равна 1.
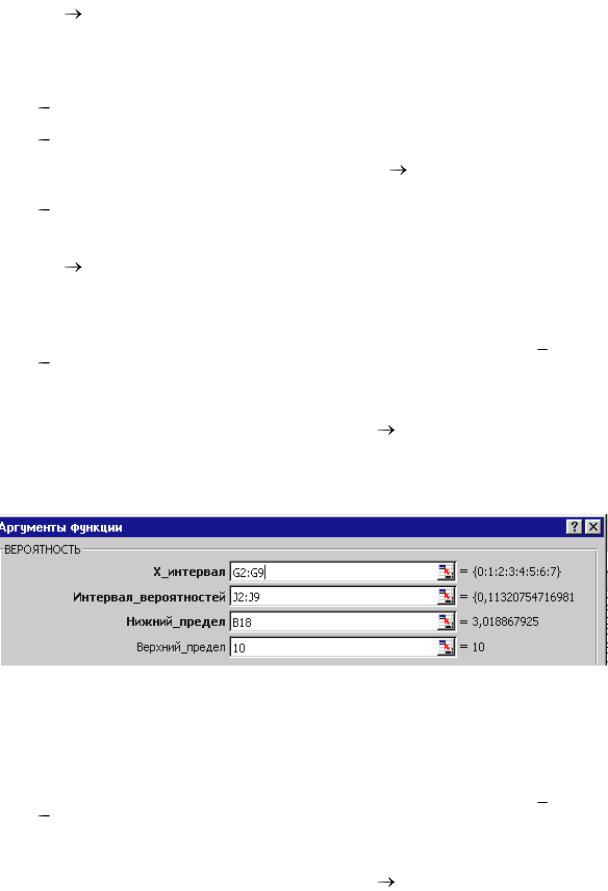
5. Находим, какая часть студентов от общего числа пропустила не более трех занятий (или 1, или 2, или 3). Для этого:
 установим курсор в ячейку F12, обращаемся к Мастеру функций, находим функцию ВЕРОЯТНОСТЬ ОК;
установим курсор в ячейку F12, обращаемся к Мастеру функций, находим функцию ВЕРОЯТНОСТЬ ОК;
Функция ВЕРОЯТНОСТЬ вычисляет вероятность того, что случайно выбранное число будет равно одному из чисел в заданном массиве значений или будет лежать внутри заданного интервала. Синтаксис этой функции имеет вид: ВЕРОЯТНОСТЬ(х_интервал; интервал_вероятностей; нижний_предел; верхний _предел).
 заполним поля в открывшемся диалоговом окне Аргументы функции:
заполним поля в открывшемся диалоговом окне Аргументы функции:
здесь аргумент Х_интервал – это диапазон значений вариант выборки (D2:D8); Интервал_вероятностей – диапазон значений относительных частот выборки (F2:F8); Нижний_предел и верхний_предел – границы диапазона (1≤xi≤3).
6. Находим, какая часть студентов пропустила более трёх занятий. Для этого:
36
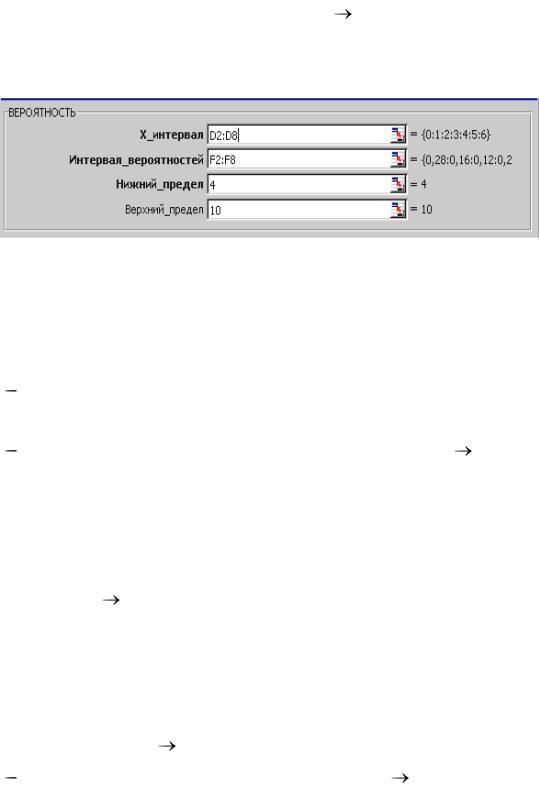
 установим курсор в ячейку F13, обращаемся к Мастеру функций, находим функцию ВЕРОЯТНОСТЬ ОК;
установим курсор в ячейку F13, обращаемся к Мастеру функций, находим функцию ВЕРОЯТНОСТЬ ОК;
 заполним поля в открывшемся диалоговом окне Аргументы функции:
заполним поля в открывшемся диалоговом окне Аргументы функции:
здесь нижний предел интервала задан числом 4 (т.к. xi >3), верхний предел задан произвольным числом, большим максимального значения варианты выборки.
7.Построим график распределения – полигон частот. Для этого:
установим курсор в свободную ячейку. Обратимся к Мастеру
диаграмм: |
|
выберем тип диаграммы – график, четвертый вид |
Далее; |
 установим переключатель в позицию Ряды в столбцах. Установим курсор в поле Диапазон и выделим мышкой диапазон Е2:Е8. Перейдем на вкладку Ряд;
установим переключатель в позицию Ряды в столбцах. Установим курсор в поле Диапазон и выделим мышкой диапазон Е2:Е8. Перейдем на вкладку Ряд;
 установим курсор в поле Подписи оси Х и выделим мышкой диапазон D2:D8 Далее;
установим курсор в поле Подписи оси Х и выделим мышкой диапазон D2:D8 Далее;
 на вкладке Заголовки введём с клавиатуры название диаграммы, подписи осей; на вкладке Подписи данных поставим флажок в поле
на вкладке Заголовки введём с клавиатуры название диаграммы, подписи осей; на вкладке Подписи данных поставим флажок в поле
Значения; на вкладке Легенда снимем флажок в поле Добавить легенду. На вкладке Линии сетки установим флажок в позиции Ось Х:
промежуточные линии Далее;
поместим диаграмму на имеющемся листе Готово;
 наведя курсор на ось Х, двойным щелчком мышки выведем на экран диалоговое окно Формат оси. На вкладке Шкала снимем флажок в поле Пересечение с осью Y между категориями;
наведя курсор на ось Х, двойным щелчком мышки выведем на экран диалоговое окно Формат оси. На вкладке Шкала снимем флажок в поле Пересечение с осью Y между категориями;
37
отформатируем элементы диаграммы (размер, шрифт, цвет).
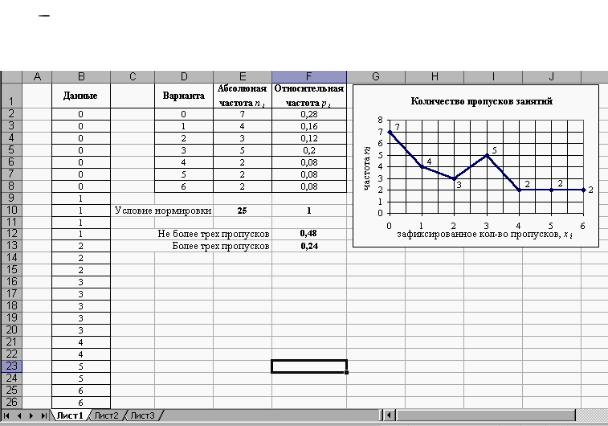
8.Сравним полученные результаты работы с образцом:
Выводы:
а) число пропусков занятий по дисциплине варьируется от 0 до 6 – это значения наблюдаемых в выборке вариант;
б) максимальное зарегистрированное количество пропусков – 6, т.к. xmax=6, а количество студентов пропускающих максимальное количество занятий соответственно составляет 8% от общего числа студентов (т.к.
р*(xmax)=0,08);
в) часть студентов от общего числа, не пропускающих занятия, составляет 28%, что соответствует значению р*(x=0)=0,28;
г) часть студентов от общего числа, пропускающих по три и меньше занятий, составляет 48% (что соответствует значению ячейки F12, равному
0,48);
д) часть студентов от общего числа, пропускающих более трёх занятий, составляет 24% (что соответствует значению ячейки F13, равному
0,24).
38

2.2. Статистические оценки параметров распределения
Статистическими оценками вероятностных характеристик генеральной совокупности называют приближённые значения этих характеристик, полученные в результате обработки статистических данных.
Пусть одна из характеристик случайной величины X найдена приближенно, путём произведённых независимых опытов (испытаний),
обозначим ее * . Тогда случайная величина * − статистическая оценка неизвестного параметра теоретического распределения количественного признака генеральной совокупности.
Статистическая оценка должна удовлетворять трём основным требованиям: несмещённости, эффективности и состоятельности.
Несмещённой называют статистическую оценку |
* , математическое |
ожидание которой равно оцениваемому параметру |
при любом объёме |
выборки, т.е. M ( * ) 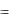 .
.
Эффективной называют статистическую оценку, которая (при заданном объёме выборки n) имеет наименьшую возможную дисперсию.
Состоятельной называют статистическую оценку, которая при n  стремится, по вероятности, к оцениваемому параметру.
стремится, по вероятности, к оцениваемому параметру.
Параметр |
Статистическая |
|
|
|
Формула |
|
|
|
|||||||||||||
|
оценка параметра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность Р |
Относительная частота W |
|
|
|
|
W A |
|
m |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
n |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
Математическое |
Среднее выборочное |
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
ni xi |
||
xВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ожидание М(Х) |
|
x В |
i 1 |
|
, или |
|
x В |
|
i 1 |
|
|||||||||||
|
|
|
|
|
n |
|
|
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
Дисперсия D(X) |
Выборочная дисперсия |
DВ |
|
|
|
D |
|
|
x |
|
|
|
x |
В |
|
||||||
|
|
|
|
|
|
|
|
В |
|
|
|
В |
|
|
|
|
|
|
|
||
Среднее |
Выборочное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратическое |
среднее квадратическое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
В |
|
|
DВ . |
|
|
|
||||||||||
отклонение ( X ) |
отклонение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39
В мастере функций Ехсеl имеется ряд специальных функций, предназначенных для вычисления выборочных характеристик. Прежде всего, это функции, характеризующие центр распределения.
 Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов чисел. Синтаксис функции:
Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов чисел. Синтаксис функции:
СРЗНАЧ(число1;число2;…), где аргументы число1; число2… —
это числа, образующие набор данных (выборочную совокупность), для которого вычисляется средняя. Например, если ячейки А1:А7 содержат числа 10, 14, 5, 6, 10, 12 и 13, то их среднее арифметическое СРЗНАЧ(А1:А7) равно 10.
 Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана Me — это элемент выборки, который делит
Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана Me — это элемент выборки, который делит
вариационный ряд |
на две части, равные по числу вариант. |
Синтаксис функции: |
МЕДИАНА(число1;число2;...), где аргументы |
число1; число2;... — от 1 до 30 чисел, для которых определяется медиана. Например, если ячейки А1:А6 содержат числа 2, 3, 5, 6, 7 и 9, то МЕДИАНА(А1:А6) равна 5,5.
 Функция МОДА вычисляет наиболее часто встречающееся значение в выборке. Синтаксис функции: МОДА(число1;число2;...), где аргументы число1; число2;... — от 1 до 30 чисел, для которых определяется мода. Например, если ячейки А1:А6 содержат числа 2, 3, 5, 2, 7 и 9, то МОДА(А1:А6) равна 2.
Функция МОДА вычисляет наиболее часто встречающееся значение в выборке. Синтаксис функции: МОДА(число1;число2;...), где аргументы число1; число2;... — от 1 до 30 чисел, для которых определяется мода. Например, если ячейки А1:А6 содержат числа 2, 3, 5, 2, 7 и 9, то МОДА(А1:А6) равна 2.
К специальным функциям, вычисляющим выборочные характеристики, характеризующие рассеяние вариант, относятся ДИСП, СТАНДОТКЛОН.
 Функция ДИСП позволяет оценить дисперсию по выборочным данным. Синтаксис функции: ДИСП(число1;число2…), где аргументы число1; число2… − это числа, образующие набор данных (выборочную совокупность), для которого вычисляется дисперсия. Например, ДИСПР(10; 14; 5; 6; 10; 12; 13) равняется 10.
Функция ДИСП позволяет оценить дисперсию по выборочным данным. Синтаксис функции: ДИСП(число1;число2…), где аргументы число1; число2… − это числа, образующие набор данных (выборочную совокупность), для которого вычисляется дисперсия. Например, ДИСПР(10; 14; 5; 6; 10; 12; 13) равняется 10.
40
 Функция СТАНДОТКЛОН вычисляет стандартное отклонение.
Функция СТАНДОТКЛОН вычисляет стандартное отклонение.
Синтаксис функции СТАНДОТКЛОН(число1;число2…), где аргументы число1;число2… − это числа, образующие набор данных (выборочную совокупность), для которого вычисляется стандартное отклонение. Например, СТАНДОТКЛОН(10; 14; 5; 6; 10; 12; 13) равняется 3,41565.
Пример 1
Выборочное обследование правильности оформления налоговых деклараций индивидуальными предпринимателями в течение года выявило следующие результаты:
0, 3, 6, 5, 4, 1, 2, 6, 4, 3, 2, 1, 7, 3, 3, 4, 2, 0, 1, 0, 3, 2, 1, 3, 0, 5, 4, 0, 3, 4, 7, 3, 4, 2, 1, 0, 7, 3, 4, 1, 5, 6, 3, 2, 4, 1, 3, 5, 7, 4, 2, 3, 1.
Т.е. в первую неделю года нарушений не зафиксировано, во вторую неделю года зафиксировано 3 нарушения и т.д.
Провести первичную обработку статистических данных о выявленных нарушениях:
1.Составить статистическое распределение выборки.
2.Составить распределение относительных частот.
3.Определить среднее количество нарушений в неделю.
4.Построить гистограмму частот.
Решение
1.Заносим статистические данные на лист Excel.
2.Надстройка Пакет анализа содержит инструмент Гистограмма,
спомощью которого можно быстро создать распределение частот и построить гистограмму. Перед тем как запустить в работу инструмент Гистограмма, необходимо предварительно определить диапазон интервалов, по которому будет построено распределение частот.
41
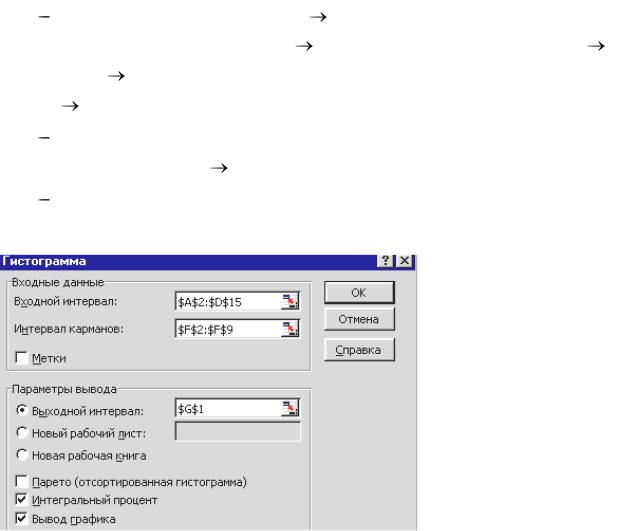
Для этого:
 установим курсор в ячейку F1, введём текст Интервалы, затем в диапазон F2:F9 введём значения наблюдаемых вариант в порядке
установим курсор в ячейку F1, введём текст Интервалы, затем в диапазон F2:F9 введём значения наблюдаемых вариант в порядке
возрастания; |
|
|
|
|
|
|
|
выполним команду Сервис |
Анализ данных (если надстройка |
||||
Пакет |
анализа |
не подключена |
выполнить команду |
Сервис |
||
Надстройки |
установить флажок в поле Пакет анализа, затем команду |
|||||
Сервис |
Анализ данных); |
|
|
|
|
|
|
в открывшемся диалоговом окне Анализ данных выберем |
|||||
инструмент Гистограмма ОК; |
|
|
|
|
||
|
в открывшемся диалоговом окне Гистограмма определим |
|||||
несколько параметров: |
|
|
|
|
||
|
|
|
■ |
в |
поле Входной |
|
|
|
|
интервал |
укажем |
||
|
|
|
диапазон с входными |
|||
|
|
|
данными А2:D15; |
|||
|
|
|
■ |
в |
поле |
Интервал |
|
|
|
карманов |
укажем |
||
|
|
|
диапазон |
интервалов |
||
|
|
|
F2:F9; |
|
||
■флажок Метки устанавливают, если первая строка исходного диапазона содержит названия полей − в нашем случае нет;
■с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим переключатель в позицию Выходной интервал, в соответствующем поле укажем ячейку G1.
Последние три флажка определяют параметры гистограммы:
-флажок Парето (отсортированная гистограмма) устанавливают,
если требуется получить гистограмму, у которой все столбцы отсортированы по убыванию – в нашем случае нет;
-флажок Интегральный процент устанавливают, если на гистограмме
42
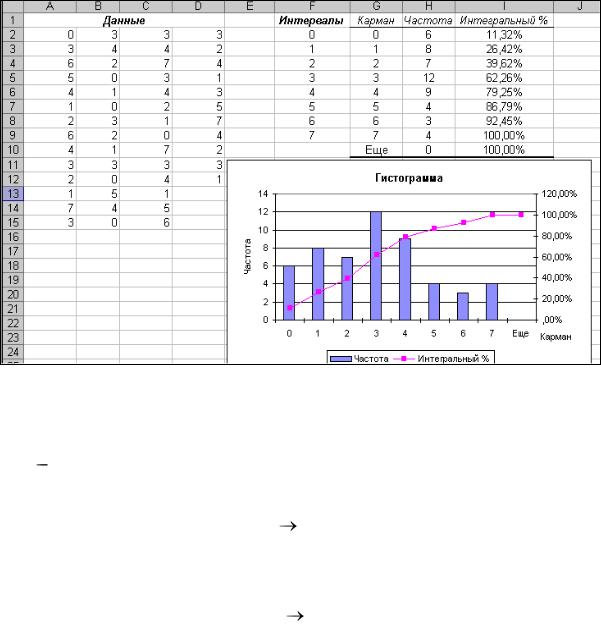
необходимо отобразить линию, точки которой обозначают нарастающее количество значений в процентном отношении (т.е. аналог функции распределения) – устанавливаем флажок;
- флажок Вывод графика устанавливают, если вместе с распределением частот нужно создать гистограмму – устанавливаем флажок.
 после того, как все необходимые параметры заданы, щелкаем по кнопке ОК – Excel создаст распределение частот и построит гистограмму.
после того, как все необходимые параметры заданы, щелкаем по кнопке ОК – Excel создаст распределение частот и построит гистограмму.
3.Находим объём выборки. Для этого:
устанавливаем курсор в ячейку А17, вносим текст n=;
 устанавливаем курсор в ячейку В17, обращаемся к Мастеру функций, находим функцию СЧЕТ ОК;
устанавливаем курсор в ячейку В17, обращаемся к Мастеру функций, находим функцию СЧЕТ ОК;
 в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Значение1 и указателем мышки выделяем диапазон исходных данных А2:D15 ОК.
в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Значение1 и указателем мышки выделяем диапазон исходных данных А2:D15 ОК.
4.Проверяем условие нормировки:
43

 устанавливаем курсор в ячейку Н11 и выполняем суммирование данных диапазона Н2:Н9. Полученное значение должно быть равно объёму выборки.
устанавливаем курсор в ячейку Н11 и выполняем суммирование данных диапазона Н2:Н9. Полученное значение должно быть равно объёму выборки.
5. Находим относительные частоты и проверяем условие нормировки. Для этого:
устанавливаем курсор в ячейку J1 и вводим текст
Относительная частота p*i;
 для вычисления относительных частот создадим формулу массива. Для этого:
для вычисления относительных частот создадим формулу массива. Для этого:
-выделим диапазон J2:J9 (начиная с ячейки J2);
-нажмём кнопку равно (=);
-выделим диапазон H2:H9;
-нажмём на кнопку деление (/), затем щёлкнем по ячейке В17  нажмём сочетание клавиш Ctrl + Shift + Enter; диапазон J2:J9 заполнится значениями относительных частот;
нажмём сочетание клавиш Ctrl + Shift + Enter; диапазон J2:J9 заполнится значениями относительных частот;
 для проверки условия нормировки, установим курсор в ячейку J11 и выполним суммирование диапазона относительных частот (J2:J9). Сумма диапазона должна быть равна 1.
для проверки условия нормировки, установим курсор в ячейку J11 и выполним суммирование диапазона относительных частот (J2:J9). Сумма диапазона должна быть равна 1.
6.Находим среднее выборочное значение хв . Для этого:
устанавливаем курсор в ячейку А18 и вносим текст хв =;
 устанавливаем курсор в ячейку В18, обращаемся к Мастеру функций и находим функцию СРЗНАЧ ОК;
устанавливаем курсор в ячейку В18, обращаемся к Мастеру функций и находим функцию СРЗНАЧ ОК;
 в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Число1 и мышкой выделяем диапазон данных
в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Число1 и мышкой выделяем диапазон данных
А2:D15 ОК.
7.Находим дисперсию выборочных данных Dв. Для этого:
устанавливаем курсор в ячейку А19 и вводим текст Dв=;
 устанавливаем курсор в ячейку В19, обращаемся к Мастеру функций и находим функцию ДИСП ОК;
устанавливаем курсор в ячейку В19, обращаемся к Мастеру функций и находим функцию ДИСП ОК;
в открывшемся диалоговом окне Аргументы функции
44
устанавливаем курсор в поле Число1 и мышкой выделяем диапазон данных
А2:D15 ОК.
8. Находим выборочное среднее квадратическое отклонение σв. Для этого:
устанавливаем курсор в ячейку А20 и вводим текст σв=;
устанавливаем курсор в ячейку В20, обращаемся к Мастеру
функций и находим функцию СТАНДОТКЛОН |
ОК; |
в открывшемся диалоговом окне |
Аргументы функции |
устанавливаем курсор в поле Число1 и мышкой выделяем диапазон данных
А2:D15 |
ОК. |
9. |
Находим, какую часть от общего времени наблюдения |
фиксировалось количество нарушений выше среднего уровня. Для этого:
устанавливаем курсор в ячейку А21 и вводим текст Р*(X> хв )=;
 устанавливаем курсор в ячейку В21, обращаемся к Мастеру функций и находим функцию ВЕРОЯТНОСТЬ ОК;
устанавливаем курсор в ячейку В21, обращаемся к Мастеру функций и находим функцию ВЕРОЯТНОСТЬ ОК;
 в открывшемся диалоговом окне Аргументы функции заполняем поля в соответствии с рисунком:
в открывшемся диалоговом окне Аргументы функции заполняем поля в соответствии с рисунком:
здесь аргумент Верхний_предел равен произвольно заданному числу, большему, чем максимальное значение, наблюдаемое в выборке.
10. Находим, какую часть от общего времени наблюдения фиксировалось количество нарушений ниже среднего уровня. Для этого:
устанавливаем курсор в ячейку А22 и вводим текст Р*(X< хв )=;
 устанавливаем курсор в ячейку В22, обращаемся к Мастеру функций и находим функцию ВЕРОЯТНОСТЬ ОК;
устанавливаем курсор в ячейку В22, обращаемся к Мастеру функций и находим функцию ВЕРОЯТНОСТЬ ОК;
45
 в открывшемся диалоговом окне Аргументы функции заполняем поля в соответствии с рисунком:
в открывшемся диалоговом окне Аргументы функции заполняем поля в соответствии с рисунком:
11. Проанализируем полученные результаты:
В налоговой инспекции в течение 53 недель фиксировались данные о нарушениях при оформлении налоговых деклараций индивидуальными предпринимателями. Проведя предварительную статистическую оценку полученных данных можно сделать следующие выводы:
1. Еженедельное количество нарушений варьировалось в интервале от
0 до 7 (см. значения вариант выборки).
46

2. В среднем еженедельное количество нарушений, фиксируемое в инспекции, может быть принято как 3 нарушения с разбросом ±2
нарушения (см. значения хв и σв).
3.В течение 6 недель года нарушений зафиксировано не было, что составило 11% от общего времени наблюдения (см. значения интервала
G2:J2).
4.Максимальное количество нарушений – 7, фиксировалось в течение 4 недель, это составило 8% от общего времени наблюдения (см.
значения интервала G9:J9).
5.В течение 20 недель года фиксировалось количество нарушений, превышающее среднее значение, что соответствует 38% от общего времени наблюдения (см. значения ячейки В21 и диапазона G6:J9).
6.Количество нарушений ниже среднего уровня фиксировалось в течение 27 недель года – это 51% от времени наблюдения (см. значения ячейки В22 и диапазона G3:J5).
7.Наиболее часто (12 недель) еженедельно фиксировалось по 3 нарушения, что составляет 23% от времени наблюдения (см. значения интервала G5:J5).
В пакете Ехсеl помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
Для установки раздела Анализ данных в пакете Ехсеl необходимо выполнить следующее:
 в меню Сервис выберите команду Надстройки;
в меню Сервис выберите команду Надстройки;  в появившемся списке установите флажок Пакет анализа.
в появившемся списке установите флажок Пакет анализа.
Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Ехсеl информация вводится в отдельные ячейки.
47
Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.
Последовательность обработки данных. Для использования статистического пакета анализа данных необходимо:
 указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
 в раскрывающемся списке выбрать команду Анализ данных;
в раскрывающемся списке выбрать команду Анализ данных;
 выбрать необходимую строку в появившемся списке
выбрать необходимую строку в появившемся списке
Инструменты анализа;
 ввести входной и выходной диапазоны и выбрать необходимые параметры.
ввести входной и выходной диапазоны и выбрать необходимые параметры.
Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Для выполнения процедуры необходимо:
 выполнить команду Сервис → Анализ данных;
выполнить команду Сервис → Анализ данных;
 в появившемся списке Инструменты анализа выбрать строку
в появившемся списке Инструменты анализа выбрать строку
Описательная статистика и нажать кнопку ОК;
 в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные;
в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные;
 указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;
указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;
 в разделе Группировка переключатель установить в положение по столбцам;
в разделе Группировка переключатель установить в положение по столбцам;
 установить флажок в поле Итоговая статистика;
установить флажок в поле Итоговая статистика;
 нажать кнопку ОК.
нажать кнопку ОК.
48

В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.
Пример 2
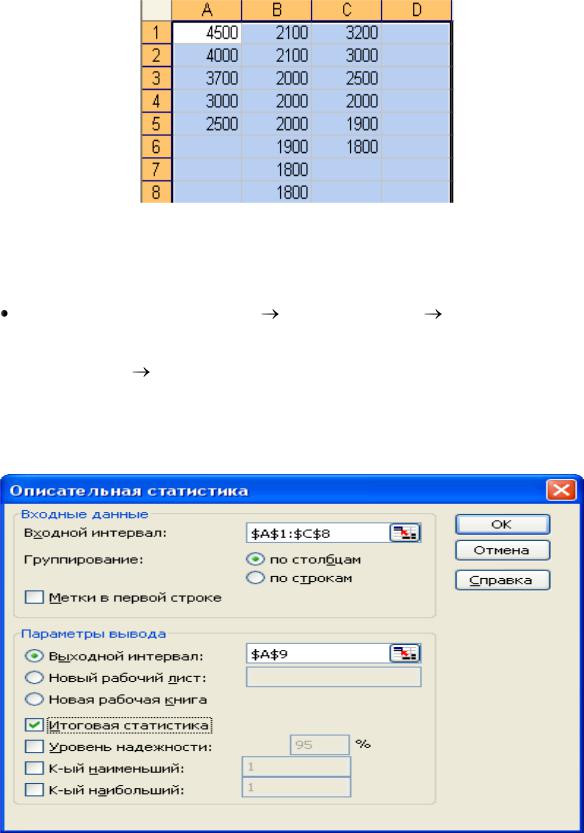
Провести статистическую обработку собранных данных о заработной плате (у.е.) основных групп работников гостиницы: администрации, обслуживающего персонала и работников ресторана.
Администрация |
Персонал |
Ресторан |
|
|
|
4500 |
2100 |
3200 |
|
|
|
4000 |
2100 |
3000 |
|
|
|
3700 |
2000 |
2500 |
|
|
|
3000 |
2000 |
2000 |
|
|
|
2500 |
2000 |
1900 |
|
|
|
|
1900 |
1800 |
|
|
|
|
1800 |
|
|
|
|
|
1800 |
|
|
|
|
Решение
1. Заносим статистические данные на лист Excel:
данные первой выборки размещаем в диапазоне А1:А5;
данные второй выборки размещаем в диапазоне В1:В8;
 данные третьей выборки размещаем в диапазоне С1:С6. В результате получится следующая таблица:
данные третьей выборки размещаем в диапазоне С1:С6. В результате получится следующая таблица:
49
2. |
Далее |
необходимо провести элементарную |
статистическую |
|
обработку. Для этого: |
|
|
||
выполним команду Сервис |
Анализ данных |
в открывшемся |
||
диалоговом окне Анализ данных выберем инструмент Описательная |
||||
статистика |
ОК; |
|
|
|
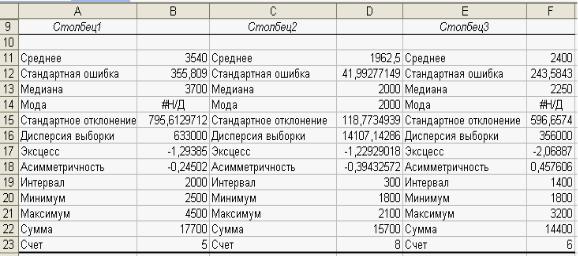
 в диалоговом окне Описательная статистика необходимо определить следующие параметры:
в диалоговом окне Описательная статистика необходимо определить следующие параметры:
в поле Входной интервал укажем диапазон с исходными данными (А1:С8). Заметим, что инструмент Описательная
статистика правильно определит размеры выборок,
50
игнорируя пустые ячейки;
укажем способ расположения записей – по столбцам, установив переключатель Группирование в соответствующее положение;
с помощью переключателя Параметры вывода определим место, куда будут определены выходные значения – в позицию
Выходной интервал;
установив курсор в поле Выходной интервал, мышкой укажем ячейку А9;
чтобы определить, какие показатели должны быть вычисленными, используем флажки расположенные внизу окна. Установим флажок Итоговая статистика, чтобы получить основные статистические характеристики.
3.После того как все параметры заданы, щёлкнем по кнопке ОК, Excel выполнит все необходимые вычисления и разместит результаты на листе.
УПРАЖНЕНИЯ
1.Найти наиболее популярный туристический маршрут из четырех реализуемых фирмой (моду), если за неделю последовательно были реализованы следующие маршруты (приводятся номера маршрутов):
1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4, 1, 4, 4, 3, 1, 2, 3, 4, 1, 1, 3.
51
2.Из большой группы предприятий одной из отраслей промышленности случайным образом отобрано 30, по которым получены показатели стоимости основных фондов (млн. руб.): 2; 3; 2; 4; 5; 2; 3; 3; 6; 4; 5; 4; 6; 5; 3; 4; 2; 4; 3; 3; 5; 4; 6; 4; 5; 3; 4; 3; 2; 4.
Провести первичную обработку статистических данных.
3.Получены результаты выборочного обследования по выполнению
плана выработки на одного рабочего (%):
90,0 |
96,0 |
98,0 |
98,0 |
98,5 |
99,0 |
101,5 |
102 |
102,0 |
102,5 |
103,0 |
103,5 |
104,0 |
||||
104,0 |
104 |
104,5 |
105,5 |
106,0 |
108,0 |
108,2 |
108,7 |
109,0 |
112 |
113,5. |
|
|||||
Составить интервальное распределение выборки с началом x0 |
90 и |
|||||||||||||||
длиной частичного интервала h=5. Построить гистограмму частот.
4.Для прогнозирования спроса на свою продукцию предприятие проводит исследование, в результате которого получены данные о размере реализованной продукции за некоторый период времени
(тыс. руб.):
42,5 |
60,0 |
63,5 |
70,5 |
82,0 |
83,5 |
92,0 |
95,5 |
100,0 |
101,0 |
105,0 |
108,5 |
||||||||
110,0 |
115,5 |
120,0 |
130,0 |
138,5 |
140,0 |
142,0 |
150,5 |
160,0 |
162,1 |
180,5. |
|||||||||
Провести первичную обработку статистических данных.
5.Имеются данные о числе тонн грузов, перевозимых еженедельно паромом некоторого морского порта в период навигации:
398, |
412, |
560, |
474, |
544, |
690, |
587, |
600, |
613, |
457, |
504, |
477, |
530, |
641, |
359, |
566, |
452, |
633, |
474, |
499, |
580, |
606, |
344, |
455, 505, |
396, |
347, |
441, |
|
390, |
632, |
400, |
582. |
|
|
|
|
|
|
|
|
|
|
Провести первичную обработку статистических данных.
2.3. Проверка статистических гипотез
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.
Например, статистическими являются гипотезы:
1)генеральная совокупность распределена по закону Пуассона;
2)дисперсии двух нормальных совокупностей равны между собой.
52

В первой гипотезе сделано предположение о виде неизвестного
распределения, во второй – о параметрах двух известных распределений.
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза.
Нулевой (основной) называют выдвинутую гипотезу H 0 .
Конкурирующей (альтернативной) называют гипотезу H1 , которая противоречит нулевой.
Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что а 10 . Коротко это записывают так: H 0 : а=10; H1 : а 10 .
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Статистическим критерием называют случайную величину К, которая служит для проверки нулевой гипотезы.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу не отклоняют.
Проверка гипотезы о предлагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины – критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Критерий согласия Пирсона 2 («хи-квадрат») служит для сравнения эмпирических и теоретических частот и отвечает на вопрос: случайно ли расхождение этих частот или оно значимо?
53
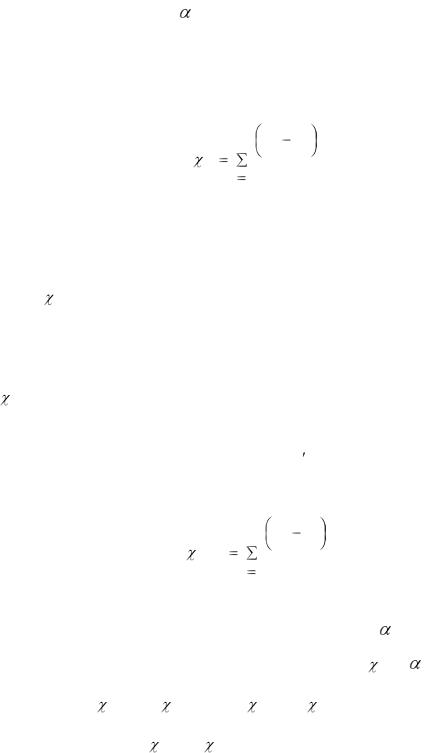
Пусть по выборке объёма n получено эмпирическое распределение
Варианты …………………… xi |
x1 |
x2 … xs |
Эмпирические частоты ……. ni |
n1 |
n2 … ns |
При уровне значимости требуется проверить нулевую гипотезу H0: генеральная совокупность распределена по предполагаемому закону.
В качестве критерия проверки нулевой гипотезы примем случайную величину
|
s |
' |
2 |
|
2 |
ni ni |
|||
|
|
|
. |
|
|
i 1 |
' |
|
|
|
|
|
||
|
ni |
|
|
|
Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Очевидно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина
критерия |
2 |
и, следовательно, разница между эмпирическим и |
|
теоретическим распределениями несущественна.
Обозначим значение критерия, вычисленное по данным наблюдений,
через |
2 |
и сформулируем алгоритм проверки нулевой гипотезы: |
|
набл |
|||
|
|
1. По предполагаемому теоретическому распределению находим выравнивающие (теоретические) частоты ni .
2. Вычисляем наблюдаемое значение критерия:
|
|
|
|
|
|
|
|
ni' |
2 |
|
|
|
|
|
|
2 |
|
s |
ni |
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
набл |
i |
1 |
|
ni' |
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
3. По данному значению уровня |
значимости |
и |
числу степеней |
|||||||||
свободы k находим критическое значение критерия |
кр2 ( |
; k). |
||||||||||
|
2 |
2 |
|
|
2 |
|
|
2 |
|
|
|
|
4. Сравниваем |
набл и |
кр |
. Если |
набл < |
|
кр |
, нет оснований отвергнуть |
|||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
нулевую гипотезу. Если |
набл |
> кр |
− нулевую гипотезу отвергают. |
|||||||||
54
Пример 1
Произведено 100 опытов. Каждый опыт состоял из 10 испытаний, в каждом из которых вероятность появления события А равна 0,3. В итоге получено следующее эмпирическое распределение (в первой строке указано число xi появлений события А в одном опыте; во второй строке – частота ni ):
|
|
xi |
|
0 |
1 |
|
2 |
|
3 |
4 |
|
5 |
|
|
|
ni |
|
2 |
10 |
|
27 |
|
32 |
23 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||||
Проверить при уровне значимости |
= 0,05, соответствие выборочных |
||||||||||||
данных биномиальному закону распределения. |
|
|
|
|
|||||||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
||
1. |
Введём значения вариант xi |
в ячейки |
А2:А7, а |
значения |
|||||||||
|
|
эмпирических частот ni |
в ячейки В2:В7. |
|
|
|
|
||||||
2. |
Найдем |
теоретические |
частоты биномиального распределения. |
||||||||||
Для этого: |
|
|
|
|
|
|
|
|
|
|
|||
Устанавливаем табличный курсор в ячейку С2. Здесь должно оказаться значение искомой вероятности.
Для получения значения вероятности воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции (fx).
В появившемся диалоговом окне Мастер функций-шаг 1 из 2 в поле Категория указаны виды функций. Выбираем Статистическая. В поле Функция выбираем функцию БИНОМРАСП. Нажимаем на кнопку ОК.
 Появляется диалоговое окно БИНОМРАСП. В рабочее поле Число_ вводим с клавиатуры количество успешных испытаний т (в примере — 0). В рабочее поле Испытания вводим с клавиатуры общее количество испытаний п (в примере — 10). В рабочее поле Вероятности вводим с клавиатуры вероятность успеха в отдельном испытании р (в примере — 0,3). В рабочее поле Интегральный вводим с клавиатуры вид функции распределения —
Появляется диалоговое окно БИНОМРАСП. В рабочее поле Число_ вводим с клавиатуры количество успешных испытаний т (в примере — 0). В рабочее поле Испытания вводим с клавиатуры общее количество испытаний п (в примере — 10). В рабочее поле Вероятности вводим с клавиатуры вероятность успеха в отдельном испытании р (в примере — 0,3). В рабочее поле Интегральный вводим с клавиатуры вид функции распределения —
55
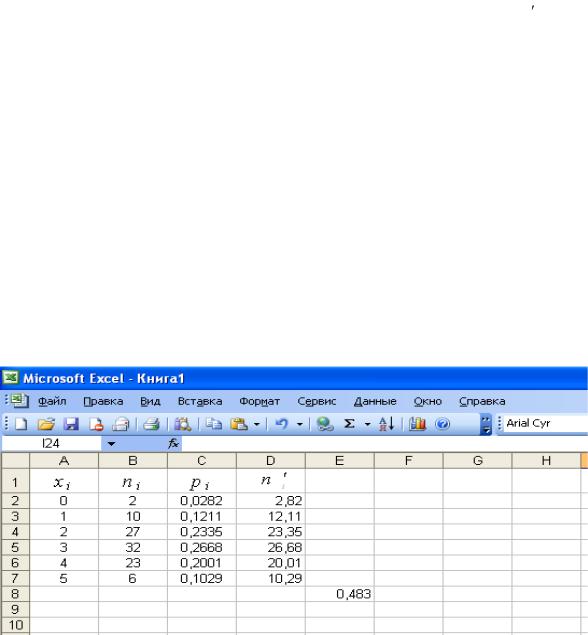
интегральная или весовая (в примере — 0). Нажимаем на кнопку ОК. В ячейке С2 появляется искомое значение вероятности р = 0,0282.
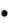 Аналогично рассчитываем вероятности P10 (1), P10 (2), P10 (3), P10 (4), P10 (5) в ячейках С3:С7.
Аналогично рассчитываем вероятности P10 (1), P10 (2), P10 (3), P10 (4), P10 (5) в ячейках С3:С7.
 В ячейках D2:D7 получим значения теоретических частот ni . Для этого умножим значения P10 (i) на 100.
В ячейках D2:D7 получим значения теоретических частот ni . Для этого умножим значения P10 (i) на 100.
3. С помощью функции ХИ2ТЕСТ определим соответствие данных биномиальному закону распределения. Для этого установите табличный курсор в свободную ячейку Е8. На панели инструментов Стандартная нажмите кнопку Вставка функции. В появившемся диалоговом окне
Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Указателем мыши в рабочие поля введите фактический В2:В7 и ожидаемые D2:D7 диапазоны частот. Нажмите кнопку ОК. В ячейке E8 появится значение вероятности того, что выборочные данные соответствуют биномиальному закону распределения – 0,483.
4. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,483 много больше, чем уровень значимости α = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат биномиальному закону распределения.
56

Пример 2
Отдел технического контроля проверил 200 партий одинаковых изделий и получил следующее эмпирическое распределение (в первой строке указано количество xi нестандартных изделий в одной партии; во второй строке – частота ni, т.е. количество партий, содержащих xi нестандартных изделий):
|
xi |
|
0 |
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
4 |
|
|
|
ni |
|
116 |
|
56 |
|
|
22 |
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Проверить, при уровне значимости |
|
|
=0,05, |
|
соответствие |
||||||||||||
выборочных данных закону распределения Пуассона. |
|
|
||||||||||||||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Введём значения вариант xi |
в |
ячейки |
А2:А6, |
а значения |
|||||||||||||
|
эмпирических частот ni в ячейки В2:В6. |
|
|
|
|
|
|
|||||||||||
|
2. Найдём |
теоретические |
частоты |
в |
предположении, что |
|||||||||||||
|
исследуемый признак распределен по закону Пуассона. |
|||||||||||||||||
|
Для этого: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
ni |
|
|
|
|
||
Рассчитаем среднюю выборочную Х в |
|
i 1 |
|
|
. Для это в ячейке В7 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
вычислим |
сумму произведений |
|
xi |
ni |
воспользовавшись |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
диалоговым |
окном |
Мастер |
|
|
|
функций→Математическая |
||||||||||||
→СУММПРОИЗВ. В поле Массив1 вносим диапазон ячеек А2:А6, в поле Массив2 – В2:В6. Нажимаем на кнопку ОК. Полученный результат делим на n=200. Получаем в ячейке В8 значение Х в = 0,6.
 Устанавливаем табличный курсор в ячейку С2. Здесь должно оказаться значение искомой вероятности.
Устанавливаем табличный курсор в ячейку С2. Здесь должно оказаться значение искомой вероятности.
Для получения значения вероятности воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции→Мастер функций→Статистическая. В поле Функция
выбираем функцию ПУАССОН. Нажимаем на кнопку ОК.
57
Появляется диалоговое окно ПУАССОН. В рабочее поле Х вводим с клавиатуры количество нестандартных деталей т (в примере — 0). В рабочее поле Среднее вводим с клавиатуры среднее выборочное Х в = 0,6. В рабочее поле Интегральный вводим 0. Нажимаем на кнопку ОК. В ячейке С2 появляется искомое значение вероятности р = 0,5488.
Аналогично рассчитываем вероятности P200 (1), P200 (2), |
P200 (3), |
P200 (4) в ячейках С3:С6. |
|
В ячейках D2:D6 получим значения теоретических частот |
ni . Для |
этого умножим значения P200 (i) на 200.
3. С помощью функции ХИ2ТЕСТ определим соответствие данных закону распределения Пуассона. Для этого установите табличный курсор в свободную ячейку Е7. На панели инструментов Стандартная нажмите кнопку Вставка функции→Мастер функций→Статистические→
ХИ2ТЕСТ, после чего нажмите кнопку ОК.
Указателем мыши в рабочие поля введите фактический В2:В6 и ожидаемые D2:D6 диапазоны частот. Нажмите кнопку ОК. В ячейке E7 появится значение вероятности того, что выборочные данные соответствуют закону распределения Пуассона – 0,246.
4. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,246 больше, чем уровень значимости α =
58

0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат закону распределения Пуассона.
Пример 3
Фирма, занимающаяся продажей товаров по каталогу, ежемесячно получает по почте заказы. На фирме имеются выборочные данные о количестве поступающих заказов в месяц:
64, 57, 63, 62, 58, 61, 63, 60, 60, 61, 65, 62,62, 60, 64, 61, 59, 59, 63, 61, 62,58, 58, 63, 61, 59, 62, 60, 60, 58, 61, 60, 63, 63, 58, 60, 59, 60, 59, 61, 62, 62, 63, 57, 61, 58, 60, 64, 60, 59, 61, 64, 62, 59, 65
Требуется:
1)Построить статистическое распределение выборки.
2)Выдвинуть гипотезу о виде закона распределения количества поступающих заказов.
3)Проверить гипотезу по критерию согласия Пирсона при уровне значимости = 0,05.
Решение
I.Построим статистическое распределение выборки.
1.Заносим статистические данные на лист Excel:
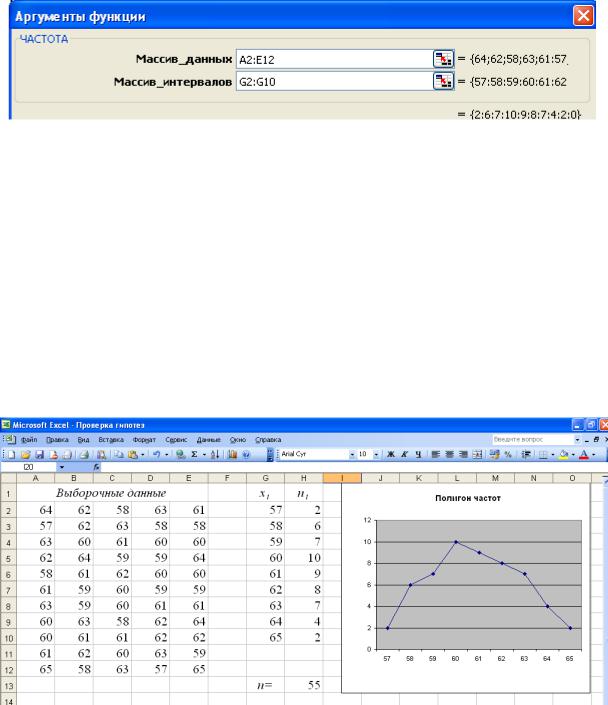
 установим курсор в ячейку А1 и введем текст Выборочные данные;
установим курсор в ячейку А1 и введем текст Выборочные данные;  в диапазон А2:Е12 введем исходные статистические данные.
в диапазон А2:Е12 введем исходные статистические данные.
2.Установим курсор в ячейку G1 и введем текст Хi .
3.В диапазон G2:G10 запишем в порядке возрастания количество поступающих на фирму заказов Хi : 57, 58, 59, 60, 61, 62, 63, 64, 65.
4.Находим абсолютные частоты и проверяем условие нормировки. Для этого:
a)установим курсор в ячейку H1 и введем текст ni;
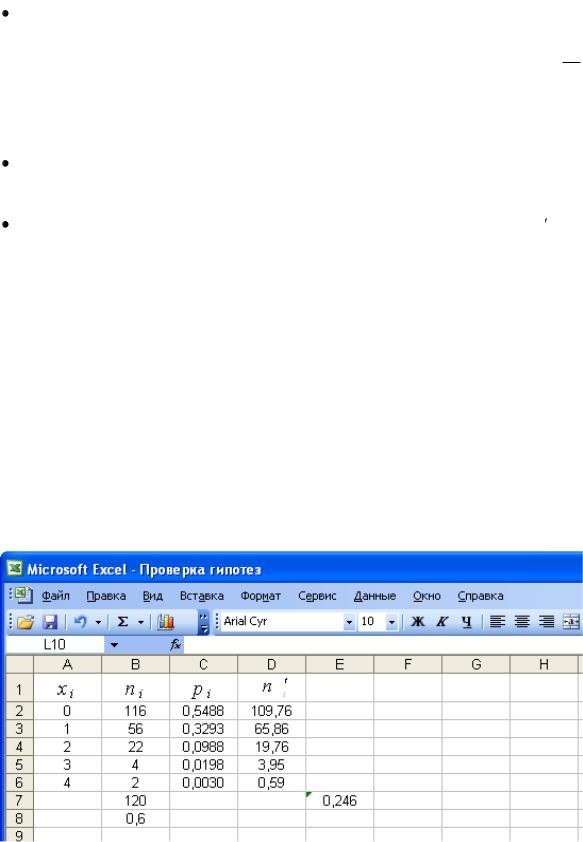
b)выделим диапазон ячеек H2:H10, вызовем Мастер функций,
находим функцию ЧАСТОТА ОК;
с) заполним поля диалогового окна Аргументы функции:
59
d) нажмём сочетание клавиш Ctrl + Shift + Enter: Диапазон H2: H10 заполнится значениями абсолютных частот.
5.Для проверки условия нормировки установим курсор в ячейку Н13
ивыполним суммирование диапазона Н2:Н10. Сумма абсолютных частот должна быть равна объёму выборки n (в нашем случае n=55);
6.Построим полигон частот и сравним полученные результаты работы с образцом:
II. По виду полигона частот выдвигаем гипотезу Но: количество поступающих на фирму заказов подчиняется нормальному закону распределения.
III. Проверим выдвинутую гипотезу Но по критерию согласия Пирсона.
60
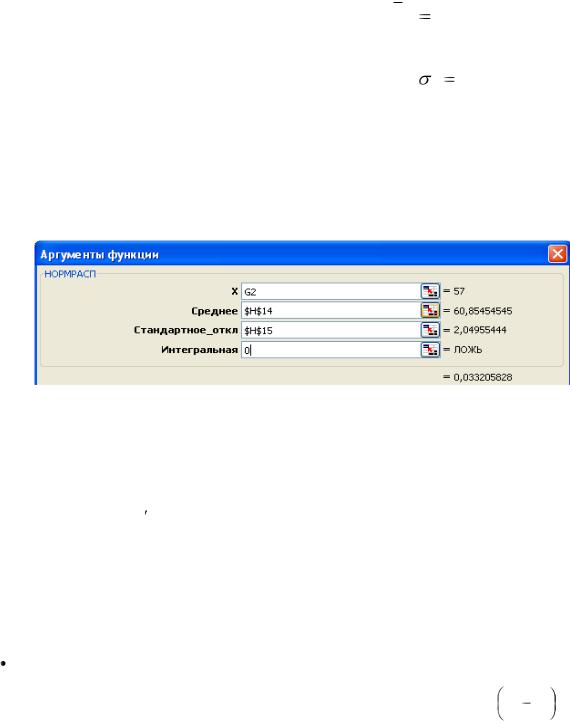
1. Найдём теоретические частоты нормального распределения. Для этого предварительно необходимо найти среднее значение и стандартное отклонение выборки.
 В ячейке Н14 с помощью функции СРЗНАЧ найдём среднее
В ячейке Н14 с помощью функции СРЗНАЧ найдём среднее
значение для данных из диапазона А2:Е12 ( x B 60,85 ).
 В ячейке Н15 с помощью функции СТАНДОТКЛОН найдём стандартное отклонение для этих же данных ( B 2,05).
В ячейке Н15 с помощью функции СТАНДОТКЛОН найдём стандартное отклонение для этих же данных ( B 2,05).
 В ячейке I1 введём название столбца – Вероятности, рi .
В ячейке I1 введём название столбца – Вероятности, рi .
 С помощью функции НОРМРАСП найдём вероятности того, что изучаемый признак имеет нормальный закон распределения. Установим курсор в ячейку I2, вызовем указанную функцию и заполним её рабочие поля по образцу:
С помощью функции НОРМРАСП найдём вероятности того, что изучаемый признак имеет нормальный закон распределения. Установим курсор в ячейку I2, вызовем указанную функцию и заполним её рабочие поля по образцу:
Получим в ячейке I2 – 0,033. Далее копируем содержимое ячейки I2 в диапазон ячеек I3:I10.
 В ячейке J1 введём название столбца – Теоретические частоты, ni .
В ячейке J1 введём название столбца – Теоретические частоты, ni .
 Установим курсор в ячейку J2 и введём формулу =Н$13*I2. Далее копируем содержимое ячейки J2 в диапазон ячеек J3:J10.
Установим курсор в ячейку J2 и введём формулу =Н$13*I2. Далее копируем содержимое ячейки J2 в диапазон ячеек J3:J10.
2. С помощью функции ХИ2ТЕСТ определим соответствие данных нормальному закону распределения. Для этого:
в ячейку К1 введём формулу расчёта относительной разности
|
n |
n |
' 2 |
|
эмпирических и теоретических частот значений признака |
i |
|
i |
|
|
|
|
; |
|
n |
' |
|
||
|
|
|
||
i
 в ячейку К2 введём формулу =(Н2-J2)^2/J2 и скопируем её в ячейки К3:К10 (протягиванием);
в ячейку К2 введём формулу =(Н2-J2)^2/J2 и скопируем её в ячейки К3:К10 (протягиванием);
61
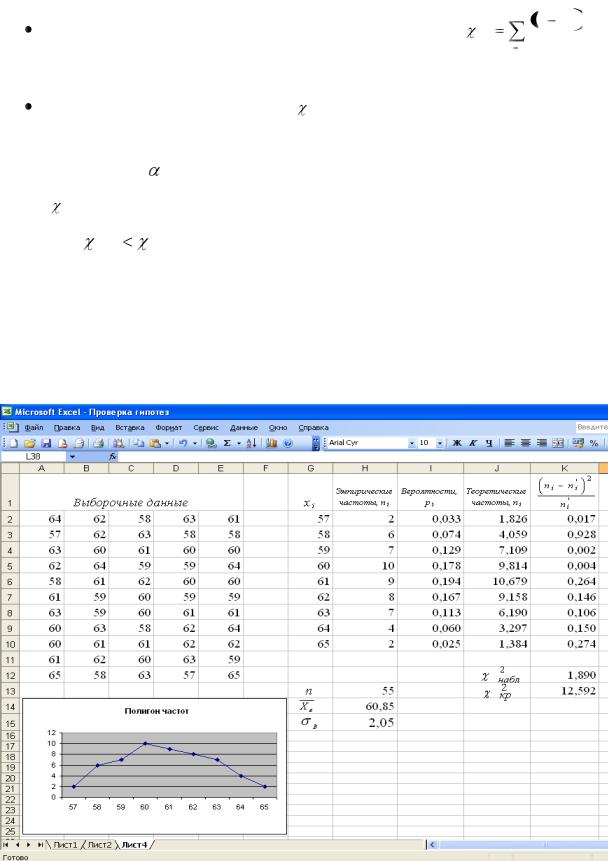
|
s |
ni |
|
' |
2 |
|
|
|
|
|
|||
в ячейку К12 введём формулу расчёта значения |
2 |
|
ni |
|
= |
|
набл |
|
n' |
|
|
||
|
|
|
|
|
||
|
i 1 |
|
i |
|
|
|
СУММ(К2:К10); |
|
|
|
|
|
|
в ячейку J13 введём текст кр2 , в ячейку K13 |
формулу расчёта |
|||||
критического значения критерия Пирсона для заданного уровня значимости = 0,05 и числа степеней свободы k = s – 3 = 9 – 3 = 6
кр2 (0,05; 6) =ХИ2ОБР(0,05;6).
3. Т.к. 2 2 , т.е. 1,89 < 12,592, то можно утверждать, что нулевая
набл кр
гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения. Другими словами, эмпирические и теоретические частоты различаются незначимо.
4. Сравним полученные результаты работы с образцом.
62
|
|
|
УПРАЖНЕНИЯ |
|
|
|
|
|
|
|
|||
1. |
На предприятии |
собраны данные о числе дней, пропущенных |
|||||||||||
работниками по болезни. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число дней, пропущенных в |
0 |
1 |
2 |
|
3 |
4 |
5 |
6 |
|
7 |
|
|
|
текущем месяце |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число работников |
2 |
3 |
10 |
|
22 |
26 |
20 |
12 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Требуется при уровне значимости 0,01 проверить гипотезу о том, |
что |
|||||||||||
выборочные данные распределены по биномиальному закону. |
|
|
|
|
|||||||||
|
2. В |
библиотеке случайно |
отобрано |
200 |
выборок |
по 5 книг. |
|||||||
Регистрировалось число повреждённых книг (подчёркивания, помарки и т.д.). В итоге получено следующее эмпирическое распределение (в первой
строке – число xi |
повреждённых книг в одной выборке, во второй строке – |
|||||||||
частота ni |
(количество выборок, содержащих xi повреждённых книг)). |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
0 |
|
1 |
2 |
3 |
4 |
5 |
|
|
ni |
|
72 |
|
77 |
34 |
14 |
2 |
1 |
|
Требуется при уровне значимости 0,05 проверить гипотезу о том, что выборочные данные распределены по закону распределения Пуассона.
3. В выборке приведена масса товаров, помещаемых в контейнер определенного размера: 21, 21, 22, 22, 22, 22, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 27, 27.
Определить соответствие экспериментальных данных нормальному закону распределения.
2.4. Корреляционно-регрессионный анализ
Статистической называют зависимость, при которой изменение одной из величин влечёт изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.
63

Другими словами, корреляционной зависимостью признака Y от X называют функциональную зависимость условного среднего y x от X , т.е. y x  f x , где y x
f x , где y x 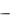 среднее арифметическое наблюдавшихся значений Y,
среднее арифметическое наблюдавшихся значений Y,
|
|
|
|
|
|
соответствующих X = x. |
Аналогично определяется условное среднее x y . |
||||
|
|
|
|
||
Уравнение y x f x , |
называется выборочным уравнением регрессии Y |
||||
на X; функцию f(x) называют выборочной регрессией Y на X , а её график –
|
|
|
|
выборочной линией регрессии Y на X. Аналогично уравнение x y |
y |
||
называется выборочным уравнением регрессии X на Y; функцию |
(x) |
||
называют выборочной регрессией X на Y , а ее график – выборочной линией регрессии X на Y.
Основные задачи теории корреляции
1. Оценить тесноту (силу) корреляционной связи.
Теснота линейной корреляционной связи между X и Y оценивается по величине выборочного коэффициента корреляции rВ признаков X и Y.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rB |
|
xy |
|
x y |
||||
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
||||
Коэффициент корреляции rВ обладает следующими свойствами: |
|||||||||||||||||
1. |
|
rВ |
|
1 , или |
1 |
rВ |
1. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||
2. |
|
Условие |
|
rВ |
|
1 |
rВ 1 является необходимым и достаточным |
||||||||||
|
|
|
|||||||||||||||
условием существования линейной функциональной зависимости. |
|||||||||||||||||
3. |
|
При |
rВ 0 |
|
линейной корреляционной связи между признаками не |
||||||||||||
существует (при этом может быть нелинейная корреляционная связь и даже нелинейная функциональная зависимость).
Таким образом, чем ближе по модулю коэффициент линейной корреляции к единице, чем теснее линейная зависимость между X и Y; чем ближе коэффициент корреляции к нулю, тем слабее линейная зависимость.
64
О тесноте связи можно судить по значению коэффициента корреляции, используя шкалу Чеддока:
Показания тесноты |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
связи |
|
|
|
|
|
|
|
|
|
|
|
Характеристика силы |
слабая |
умеренная |
заметная |
высокая |
весьма |
связи |
|
|
|
|
высокая |
|
|
|
|
|
|
|
|
|
|
|
|
2. Установить форму корреляционной связи, т.е. вид функции регрессии (линейная, квадратическая, показательная и пр.).
В случае если обе функции f(x) и (x) линейны, то корреляцию называют линейной, в противном случае нелинейной.
Уравнения линейной регрессии имеют вид
|
|
|
y |
|
|
|
|
|
|
|
x |
|
|
|
||
Y x |
y r |
x x ; |
X y |
x r |
y y . |
|||||||||||
|
|
|||||||||||||||
|
|
|
В |
|
|
|
|
|
|
|
B |
|
|
|
||
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
Пример 1
Выборочно обследовано 45 предприятий легкой промышленности по объёму промышленного производства X (млн руб.) и средней выработке на одного работника Y (тыс. руб.). Результаты представлены в таблице:
X |
Y |
|
X |
Y |
|
|
|
|
|
6,5 |
18,3 |
|
11,7 |
28,0 |
|
|
|
|
|
10,3 |
31,1 |
|
13,0 |
30,9 |
|
|
|
|
|
7,7 |
27,0 |
|
15,3 |
27,2 |
|
|
|
|
|
15,8 |
37,9 |
|
13,5 |
29,9 |
|
|
|
|
|
7,4 |
20,3 |
|
10,5 |
34,9 |
|
|
|
|
|
14,3 |
32,4 |
|
7,3 |
24,4 |
|
|
|
|
|
15,4 |
31,2 |
|
13,8 |
37,4 |
|
|
|
|
|
21,1 |
39,7 |
|
10,4 |
21,4 |
|
|
|
|
|
22,1 |
46,6 |
|
10,2 |
23,5 |
|
|
|
|
|
12,0 |
33,1 |
|
18,0 |
31,1 |
|
|
|
|
|
9,5 |
26,9 |
|
13,8 |
43,2 |
|
|
|
|
|
8,1 |
24,0 |
|
6,0 |
19,5 |
|
|
|
|
|
8,4 |
24,2 |
|
11,9 |
42,1 |
|
|
|
|
|
15,3 |
33,7 |
|
9,4 |
18,1 |
|
|
|
|
|
4,3 |
18,5 |
|
13,7 |
31,6 |
|
|
|
|
|
|
|
65 |
|
|

9,3 |
17,2 |
12,0 |
21,3 |
|
|
|
|
5,7 |
19,0 |
11,6 |
26,5 |
|
|
|
|
12,9 |
24,8 |
9,1 |
31,6 |
|
|
|
|
5,1 |
21,5 |
6,6 |
12,6 |
|
|
|
|
3,8 |
14,5 |
7,6 |
28,4 |
|
|
|
|
17,1 |
33,7 |
9,9 |
22,4 |
|
|
|
|
8,2 |
19,3 |
14,7 |
27,7 |
|
|
|
|
8,1 |
23,9 |
|
|
|
|
|
|
По данным исследования требуется:
1.Оценить тесноту линейной корреляционной связи между признаками
X и Y.
2.Составить линейные уравнения регрессии Y на X и X на Y, построить их графики.
3.Проверить гипотезу о значимости коэффициента корреляции при уровне значимости α=0,05.
Решение
1. Для оценки тесноты связи между признаками вычислим выборочный
коэффициент корреляции rв |
|
|
xy |
|
x |
y |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
||
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
xi |
|
|
|
|
6,5 10,3 |
7,7 ... |
7,6 |
|
9,9 |
14,7 |
|
|
|
|
|
||||||||||
|
x |
i 1 |
|
|
|
|
|
|
|
11,076. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y j |
|
|
|
|
18,3 |
31,1 |
27,0 |
... |
|
|
28,4 |
22,4 |
27,7 |
|
|
|
|
||||||||
|
y |
j 1 |
|
|
|
|
|
|
27,389. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i |
|
|
|
6,52 |
10,32 |
7,72 |
... |
13,82 |
10,42 10,22 |
|
|
|
||||||||||||
|
x2 |
|
|
i |
1 |
|
|
|
139,882 |
||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y |
2j |
18,32 |
31,12 |
27,02 |
|
|
... |
28,42 |
22,42 27,7 |
2 |
|
||||||||||||||
|
y2 |
|
|
j |
1 |
|
|
|
|
|
|
|
809,537. |
||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
66

|
|
45 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
xi |
y j |
6,5 18,3 10,3 31,1 ... |
9,9 22,4 14,7 27,7 |
|
|||||
|
|
i, j 1 |
|
|
|
|
|||||||
xy |
|
|
|
328,039 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
45 |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x2 |
(x)2 |
139,882 (11,076)2 |
|
4,149, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
y2 |
( y)2 |
809,537 (27,389)2 7,706. |
|
|
|
rв |
|
xy |
|
x y 328,039 11,076 27,389 |
0,772. |
|||
|
|
|
|
|
||||
|
y |
4,149 |
7,706 |
|||||
|
|
|
x |
|
||||
|
|
|
|
|
|
|
||
Полученное значение rв говорит о том, что линейная связь между объёмом промышленного производства на предприятии и средней выработкой на одного работника высокая.
2. Запишем выборочные уравнения линейной регрессии:
|
y |
|
|
y r |
|
y |
x x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||
|
x |
|
, |
|
|
x |
y |
x r |
|
y y |
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
в |
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||
Подставляя в эти |
уравнения найденные |
выше величины, |
получаем: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
7,706 |
|
|
|
|||||||||||
- уравнение регрессии Y на X: |
yx |
|
27,389 |
0,772 |
|
x |
11,076 |
|||||||||||||||||
|
4,149 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
yx |
1,434 |
x |
|
11,502 ; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
4,149 |
|
|
|
||||||||||||||
- уравнение регрессии X на Y: |
xy |
|
11,076 |
0,772 |
|
y |
27,389 |
|||||||||||||||||
|
|
7,706 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
xy 0,415792 y 0,31253 .
y 0,31253 .
Построим графики найденных уравнений регрессии (рис. 5). Точка пересечения С прямых линий имеет координаты (11,076 ; 27,389 ).
Рис. 5
67
3. Для проверки гипотезы о значимости выборочного коэффициенты корреляции сформулируем нулевую гипотезу Н0: rг=0, т.е. rв − незначим, а X и Y – некоррелированы (не связаны линейной зависимостью). Проверим гипотезу Н0 при заданном уровне значимости α=0,05.
|
|
|
|
|
|
|
|
|
Рассчитаем наблюдаемое значение критерия |
tнабл |
rB n |
2 |
|
. |
|||
|
|
|
|
|
|
|||
1 |
|
r 2 |
||||||
|
|
|
|
|
B |
|
|
|
Тогда |
tнабл. |
rв n |
2 |
0,772 |
45 2 |
7,971 |
|||||
|
|
|
|
|
|
|
|
|
|||
1 |
r2 |
1 |
0,7722 |
|
|||||||
|
|
|
|
в |
|
|
|
|
|
|
|
По таблице распределения Стьюдента при заданном уровне значимости α=0,05 и числе степеней свободы k=(n–2) найдём критическое значение критерия tкр(α, k)=2,02.
Сравниваем tнабл и tкр. Так как |tнабл|>tкр , следовательно нулевая гипотеза отвергается, т.е. коэффициент корреляции существенно отличен от нуля, значим.
Рассмотрим решение данной задачи средствами Excel.
1.Заносим статистические данные на лист Excel в диапазон ячеек А2:В46.
2.Составим уравнения регрессии Y на X и Х на Y. Для этого выберем надстройку Сервис→Анализ данных→ Регрессия→ОК. В открывшемся диалоговом окне Регрессия зададим несколько параметров:
 в поле Входной интервал Y укажем диапазон с входными данными
в поле Входной интервал Y укажем диапазон с входными данными
В1:В46;
 в поле Входной интервал X укажем диапазон с входными данными
в поле Входной интервал X укажем диапазон с входными данными
А1:А46;
 флажок Метки устанавливают, если первая строка исходного диапазона содержит название полей – в нашем случае − да;
флажок Метки устанавливают, если первая строка исходного диапазона содержит название полей – в нашем случае − да;
68
флажок Константа – ноль устанавливают, если |
требуется, чтобы |
|
линия |
регрессии проходила через начало координат – в нашем |
|
случае − нет; |
|
|
флажок |
Уровень надежности устанавливают с |
целью изменить |
уровень значимости α (Excel автоматически задает надежность γ=0,95, что соответствует уровню значимости α=1–γ=0,05). В случае α≠0,05 установите флажок и в соседнем поле введите надежность 1–α. В нашем случае этого не требуется;
 с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим переключатель в позицию Выходной интервал, в соответствующем поле укажем ячейку D1;
с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим переключатель в позицию Выходной интервал, в соответствующем поле укажем ячейку D1;
 флажок Остатки устанавливают, если требуется получить разность между фактическими и теоретическими значениями Y – не устанавливаем флажок;
флажок Остатки устанавливают, если требуется получить разность между фактическими и теоретическими значениями Y – не устанавливаем флажок;  флажок График Остатков устанавливают, если требуется получить
флажок График Остатков устанавливают, если требуется получить
диаграмму остатков для каждого значения X – не устанавливаем флажок;  флажок Стандартизованные Остатки устанавливают, если требуется получить нормированные остатки (каждый из остатков делится на
флажок Стандартизованные Остатки устанавливают, если требуется получить нормированные остатки (каждый из остатков делится на
стандартное отклонение остатков) – не устанавливаем флажок;  флажок График подбора устанавливают, если требуется получить
флажок График подбора устанавливают, если требуется получить
69
точечную диаграмму входных значений Y и значений Y, вычисленных по уравнению регрессии относительно переменной X – устанавливаем флажок;
 флажок График нормальной вероятности устанавливают, если требуется получить график нормального распределения персентиля выборки и исходных значений Y – не устанавливаем флажок.
флажок График нормальной вероятности устанавливают, если требуется получить график нормального распределения персентиля выборки и исходных значений Y – не устанавливаем флажок.
После того как все необходимые параметры заданы, щёлкаем по кнопке ОК – Excel выводит уравнение регрессии Y на Х. Аналогично составим уравнение регрессии X на Y:
70
Выводы: |
|
1. |
В графе Множественный R находится выборочный коэффициент |
корреляции rв 0,772 . Следовательно, связь между признаками Х и Y |
|
прямая и высокая. |
|
2. |
В столбце Коэффициенты находятся коэффициенты уравнений |
регрессии (свободный член и коэффициент регрессии). Таким образом, |
|
уравнения регрессии примут вид: |
|
|
yx |
|
1,434 x |
11,502 ; |
xy |
|
0,416 y 0,313 . |
3. Построим |
графики |
уравнений |
регрессии. Для этого: |
||||
– в окне полученного графика подбора щёлкаем правой кнопкой мыши по любой точке значений Y(Х), из предложенного меню выбираем
Добавить линию тренда;
– в окне линия тренда во вкладке Тип выбираем Линейная, во вкладке Параметры ставим флажок:
показывать уравнение на диаграмме;
поместить на диаграмму величину достоверности аппроксимации
(R^2)→ОК;
71
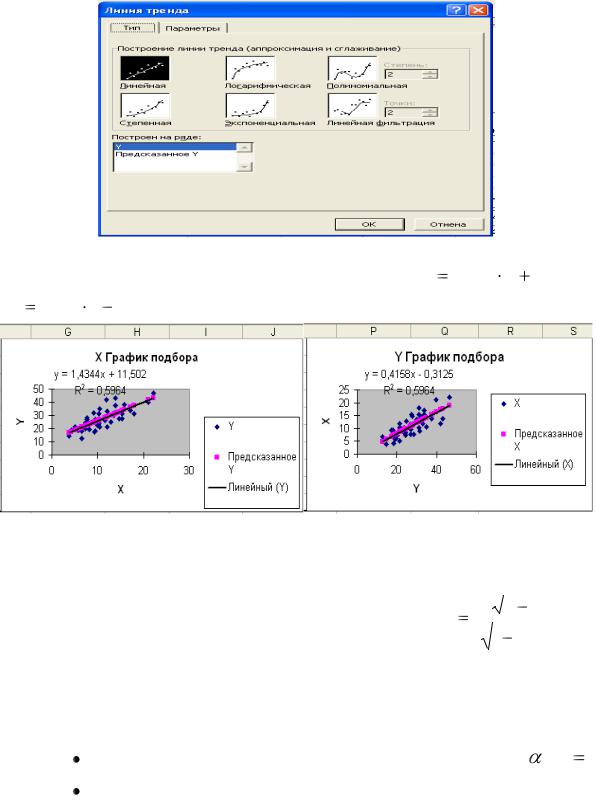
|
|
|
|
|
|
|
Графики |
уравнений |
регрессии |
yx 1,434 x 11,502 ; |
|
|
|
|
|
|
|
xy 0,416 y |
0,313 примут вид: |
|
|
|
|
4. Для проверки гипотезы о значимости выборочного коэффициенты корреляции выполним последовательность действий:
1. |
Рассчитаем наблюдаемое значение критерия tнабл |
rB |
n |
2 |
|
. Для |
||||
|
|
|
|
|
|
|||||
1 |
r 2 |
|||||||||
|
|
|
|
|
||||||
|
|
|
|
B |
|
|
|
|
|
|
|
этого устанавливаем курсор в ячейку A48 и вводим формулу |
= |
||||||||
|
0,772 *КОРЕНЬ(43)/(КОРЕНЬ(1- 0,772 * 0,772 )); |
|
|
|
|
|
|
|
|
|
2. |
Найдем критическое значение критерия tкр(α, k) . Для этого: |
|
|
|
|
|
||||
|
устанавливаем курсор в ячейку D21 и вводим текст t( |
|
|
, k) |
; |
|||||
|
устанавливаем курсор в ячейку А48, обращаемся к Мастеру |
|||||||||
|
функций и вводим функцию СТЬЮДРАСПОБР→ОК. |
|
|
|
|
|
||||
 в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Вероятность и набираем с клавиатуры число 0,05;
в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Вероятность и набираем с клавиатуры число 0,05;
72

 устанавливаем курсор в поле Степени_свободы и набираем с клавиатуры число 43 → ОК;
устанавливаем курсор в поле Степени_свободы и набираем с клавиатуры число 43 → ОК;
3. Сравниваем tнабл и tкр. Так как |tнабл|>tкр , следовательно нулевая гипотеза отвергается, т.е. коэффициент rв значим.
Криволинейная корреляция
Между признаками X и Y могут существовать и нелинейные корреляционные зависимости (параболическая, гиперболическая, показательная и пр.).
Так, например, в случае параболической корреляционной связи уравнения регрессии имеют вид:
|
|
x a1x2 a2 x a3 ; |
|
|
|
|
|
|
b1 y 2 b2 y b3 . |
||||
|
Y |
|
|
|
X y |
||||||||
В случае гиперболической корреляционной зависимости Y от X : |
|||||||||||||
|
|
|
|
|
a1 |
|
|
|
|
|
|
b1 |
b2 . |
|
|
Y x |
a2 |
; |
X y |
||||||||
|
|
x |
|
y |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Для оценки тесноты нелинейной корреляционной связи используют
выборочные корреляционные |
отношения: |
yx |
выборочное |
|
корреляционное отношение Y к |
X; xy |
выборочное |
корреляционное |
|
отношение X к Y. |
|
|
|
|
Выборочным корреляционным отношением Y к X называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:
|
межгр |
|
|
|
|
|
|
|
|
|
|
y x |
. |
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
общ |
|
|
|
y |
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Свойства выборочного корреляционного отношения |
|
||||||
1. Корреляционное отношение удовлетворяет неравенству 0 |
1. |
||||||
73

2.Если 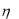 0, то признак Y с признаком X корреляционной зависимостью не связан.
0, то признак Y с признаком X корреляционной зависимостью не связан.
3.Если  1, то признак Y связан с признаком X функциональной зависимостью.
1, то признак Y связан с признаком X функциональной зависимостью.
4.Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции: 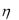
 rВ .
rВ .
Пример 2
Выборочно обследовано 15 объектов недвижимости по величине жилой площади объектов X (кв. футах) и стоимости объектов Y (тыс. долл.). Результаты представлены в таблице:
X |
Y |
|
|
521 |
26,0 |
|
|
661 |
31,0 |
|
|
694 |
37,4 |
|
|
743 |
34,8 |
|
|
787 |
39,2 |
|
|
825 |
38,0 |
|
|
883 |
39,6 |
|
|
920 |
31,2 |
|
|
965 |
37,2 |
|
|
1011 |
38,4 |
|
|
1047 |
43,6 |
|
|
1060 |
44,8 |
|
|
1079 |
40,6 |
|
|
1164 |
41,8 |
|
|
1298 |
45,2 |
|
|
По данным исследования
требуется:
1.В прямоугольной системе координат построить точечную диаграмму рассеивания признаков X и Y и сделать предположение о виде корреляционной связи.
2.Используя показательную модель составить уравнения регрессии Y на X и X на Y,
построить их графики.
74
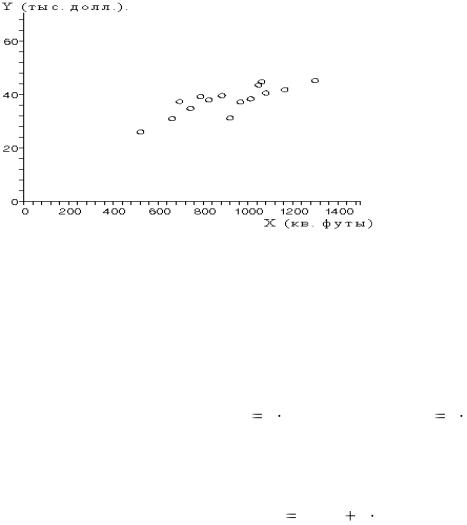
Решение
1.Для построения диаграммы рассеивания нанесём на координатную плоскость XOY точки с координатами (xi,yi), i=1,…,15.
По виду графика выдвинем гипотезу о нелинейной корреляционной зависимости признаков Х и Y и используем показательную модель для составления уравнений регрессии.
X |
Y |
Ln(X) |
Ln(Y) |
|
|
|
|
521 |
26 |
6,255 |
3,258 |
|
|
|
|
661 |
31 |
6,493 |
3,433 |
|
|
|
|
694 |
37,4 |
6,542 |
3,621 |
|
|
|
|
743 |
34,8 |
6,610 |
3,549 |
|
|
|
|
787 |
39,2 |
6,668 |
3,668 |
|
|
|
|
825 |
38 |
6,715 |
3,637 |
|
|
|
|
883 |
39,6 |
6,783 |
3,678 |
|
|
|
|
920 |
31,2 |
6,824 |
3,44 |
|
|
|
|
965 |
37,2 |
6,872 |
3,616 |
|
|
|
|
1011 |
38,4 |
6,918 |
3,648 |
|
|
|
|
1047 |
43,6 |
6,953 |
3,775 |
|
|
|
|
1060 |
44,8 |
6,966 |
3,802 |
|
|
|
|
1079 |
40,6 |
6,983 |
3,703 |
|
|
|
|
1164 |
41,8 |
7,059 |
3,732 |
|
|
|
|
1298 |
45,2 |
7,168 |
3,811 |
|
|
|
|
2. В показательной модели уравнение регрессии имеет вид:
y c xb |
|
( x c yb ). |
|
Прологарифмируем |
обе |
части |
|
данного |
|
равенства |
|
Ln( y) Ln(c) |
b Ln(x) . |
Для |
|
нахождения |
коэффициентов |
||
полученного |
|
уравнения |
|
применим обычную |
линейную |
||
регрессию |
для |
зависимой |
|
переменной |
|
Ln( y) |
и |
независимой Ln(x) .
Произведём необходимые расчёты.
75

Ln(x)
15 |
|
|
|
|
|
Lni |
(x) |
6,255 |
6,493 6,542 ... 6,983 7,059 7,168 |
|
|
i 1 |
|
6,788 |
|||
|
|
|
|
||
n |
|
|
|
15 |
|
|
|
|
|
||
Ln( y)
15 |
|
|
|
|
|
Ln j |
( y) |
|
|||
j 1 |
|
|
3,258 3,433 3,621 ... 3,703 3,732 3,811 |
3,625 |
|
n |
15 |
||||
|
|||||
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ln2 |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
6,2552 6,4932 6,5422 |
... 6,9832 |
7,0592 |
7,1682 |
|
|||
Ln2 (x) |
|
|
||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
46,129 |
||||
|
n |
|
|
15 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ln2j |
( y) |
|
|
|
|
|||||
|
|
|
j 1 |
|
|
|
|
3,2582 3,4332 ... |
3,7322 |
3,8112 |
|
|||
Ln2 ( y) |
|
|
|
13,164 |
||||||||||
|
|
n |
|
15 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Ln(x)  Ln( y)
Ln( y)
15 |
|
|
|
|
|
Lni (x) |
Ln j |
( y) |
|
||
i, j 1 |
|
|
|
6,255 3,258 6,493 3,433 6,542 3,621 |
... |
n |
|
15 |
|||
|
|
||||
7,059 |
3,732 |
7,168 |
3,811 |
24,636 |
|
… |
|
|
|
|
|
|
15 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ln( x) |
Ln2 |
(x) |
(Ln(x))2 |
46,129 |
(6,788)2 |
0,234 , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ln( y) |
|
Ln2 |
( y) |
(Ln( y))2 |
13,164 |
(3,625)2 |
0,147 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Выборочный коэффициент корреляции, таким образом, выглядит так:
|
|
|
|
|
|
|
|
|
|
|
|
|
rв |
|
Ln(x) Ln( y) |
|
Ln(x) Ln( y) 24,636 6,788 3,625 |
0,828 . |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
Ln( y) |
0,234 |
0,147 |
|
||||||||
|
|
Ln( x) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Подставим найденные значения в уравнение регрессии Ln(y) на Ln(x):
|
|
|
|
|
Ln( y) |
|
|
rв |
Ln( y) |
|
|
|
|||
Ln( y) |
|
Ln( y) rв |
|
Ln(x) |
Ln(x) , |
|
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Ln( x) |
|
|
Ln( x) |
|
|
|
|
|||
Ln( y) |
3,625 |
0,828 |
0,147 |
6,788 |
0,828 |
0,147 |
|
Ln(x) , |
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
0,234 |
|
|
|
|
0,234 |
|
|
|||
Ln( y) |
0,104 |
0,518 |
Ln(x) . |
|
|
|
|
|
|
|
|||||
76
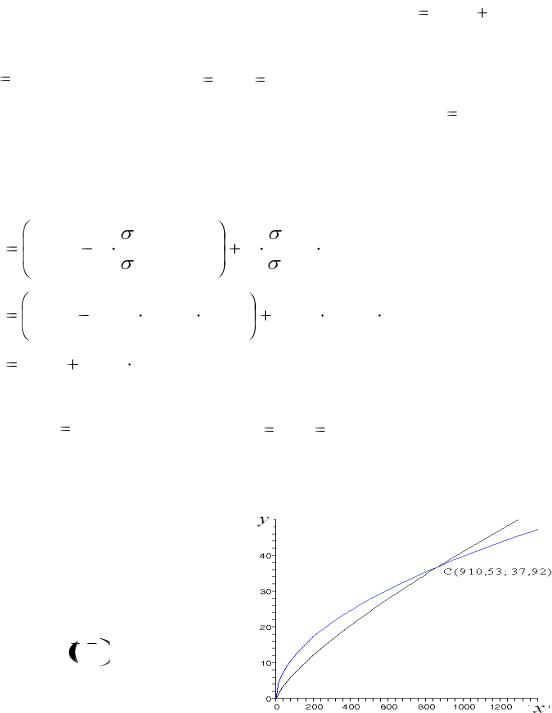
Сопоставляя полученный результат с уравнением Ln( y) Ln(c) bLn(x)
делаем вывод, что коэффициент b в показательной модели равен 0,518, а Ln(c) 0,104 , следовательно с e0,104 1,11.
Таким образом, уравнение регрессии Y на X примет вид: y 1,11 x0,518 .
x0,518 .
Аналогичные вычисления проведём для уравнения регрессии Ln(x) на
Ln(y).
|
|
|
|
|
Ln( x) |
|
|
rв |
Ln( x) |
|
|
|
|||
Ln(x) |
|
Ln(x) rв |
|
Ln( y) |
Ln( y) , |
|
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Ln( y) |
|
|
Ln( y) |
|
|
|
|
|||
Ln(x) |
6,788 |
0,828 |
0,234 |
3,625 |
0,828 |
0,234 |
|
Ln(x) |
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
0,147 |
|
|
|
|
0,147 |
|
|
|||
Ln(x) |
1,995 |
1,322 |
Ln( y) |
|
|
|
|
|
|
|
|||||
Делаем вывод, что коэффициент b в показательной модели составляет 1,322 , а Ln(c) 1,995, следовательно, с e1,995 7,352 .
Таким образом, уравнение регрессии X на Y примет вид: x = 7,352  y1,322.
y1,322.
Построим графики найденных уравнений регрессии (рис. 6).
На рисунке точка пересечения линий регрессии имеет
координаты x, y . В нашем примере С(910,53; 37,92).
Рис. 6
Рассмотрим решение данной задачи средствами Excel.
1.Заносим статистические данные на лист Excel в диапазон ячеек А2:В16.
2.Рассчитаем значения в столбцах Ln(X) и Ln(Y). Для этого:
77
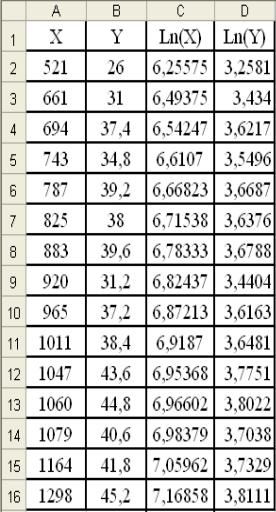
–устанавливаем курсор в ячейку С1 и вводим текст Ln(X) (в ячейке D1 вводим текст Ln(Y));
–устанавливаем курсор в ячейку С2, обращаемся к Мастеру функций и находим функцию LN→OK;
–в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Число и мышью выделяем ячейку А2→OK;
–удерживая правой кнопкой мыши, скопируем формулу во все ячейки столбца С;
–аналогично рассчитаем значения Ln(Y) в ячейках D2:D16;
–сравните полученные результаты с образцом:
3.Составим уравнение регрессии
Ln(Y) на Ln(X). Для того чтобы запустить в работу инструмент
Регрессия, необходимо:
– выполнить команду Сервис → Анализ данных (если надстройка
Пакет анализа не подключена → выполнить команду Сервис → Надстройки → установить флажок в поле Пакет анализа,
затем команду Сервис→Анализ данных);
− в открывшемся диалоговом окне Регрессия зададим несколько параметров:
78
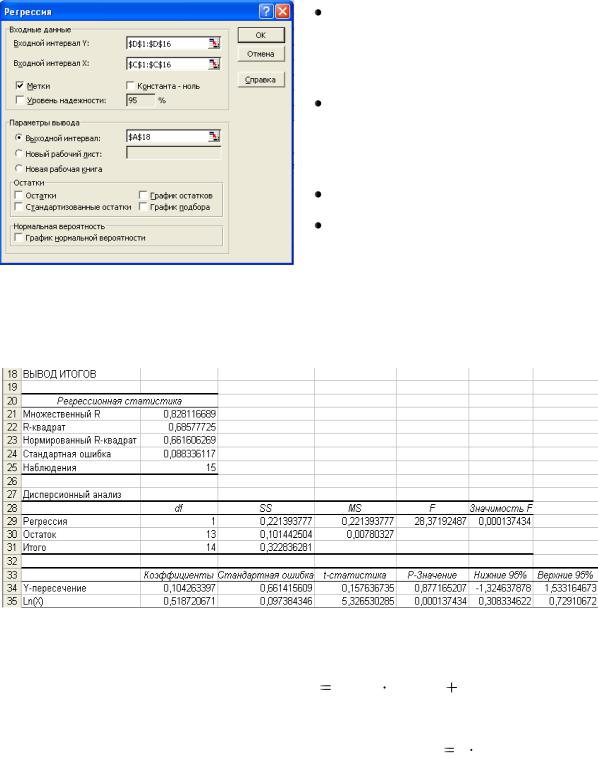
в поле Входной интервал Y
укажем диапазон с входными данными D1:D16;
в поле Входной интервал X
укажем диапазон с входными данными C1:C16;
отметим флажок Метки;
в позицию Выходной интервал
укажем ячейку А18.
– после того, как все необходимые параметры заданы, щелкаем по кнопке ОК – Excel выводит расчёты по регрессионному анализу.
Вывод: |
|
|
|
Уравнение регрессии имеет вид Ln(Y ) |
0,518 Ln( X ) |
0,104 . |
|
4. Для нахождения уравнения |
регрессии y |
c xb |
выполним |
следующее: |
|
|
|
–устанавливаем курсор в ячейку B36, обращаемся к Мастеру функций и находим функцию EXP→OK;
–в открывшемся диалоговом окне Аргументы функции устанавливаем курсор в поле Число и мышью выделяем ячейку B34→OK;
79

– полученное число 1,11 есть коэффициент с |
в уравнении y |
c xb . |
|
Таким образом, уравнение регрессии выглядит y 1,11 |
x0,518 . |
|
|
5. Аналогично получим уравнение |
регрессии |
Ln(X) |
на Ln(Y). |
Вывод:
Уравнение регрессии имеет вид Ln( X ) 1,322  Ln(Y ) 1,995 , а искомое уравнение x c
Ln(Y ) 1,995 , а искомое уравнение x c  yb выглядит так: x = 7,352
yb выглядит так: x = 7,352  y1,322.
y1,322.
Множественная корреляция
Множественная корреляция  это исследование связи между несколькими признаками. Пусть Z линейно зависит от X и Y, тогда уравнение линейной множественной регрессии имеет вид:
это исследование связи между несколькими признаками. Пусть Z линейно зависит от X и Y, тогда уравнение линейной множественной регрессии имеет вид:
z a1x a2 y a0 .
Теснота линейной корреляционной связи признака Z с X и Y
оценивается с помощью выборочного совокупного коэффициента
корреляции:
|
r 2 |
2r |
r |
r |
yz |
r 2 |
|
R |
xz |
xy |
xz |
|
yz |
. |
|
|
1 |
r 2 |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
xy |
|
|
|
|
80
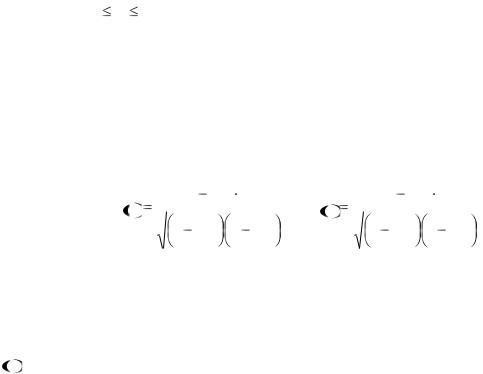
При этом 0 R 1 и при приближении R к единице теснота линейной связи Z с X и Y увеличивается.
Следующей задачей множественной корреляции является задача − оценить влияние на Z отдельно признака X и отдельно признака Y. Это осуществляется при помощи выборочных частных коэффициентов
корреляции:
rxz y |
|
rxz rxy |
z yz |
|
; |
ryz x |
|
ryz |
rxy |
rxz |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 r 2 |
1 r 2 |
|
1 r 2 |
|
1 r |
2 |
|||||||
|
|
xy |
yz |
|
|
|
|
xy |
|
xz |
||||
Первый коэффициент оценивает тесноту линейной корреляционной связи между Z и X, когда Y остается постоянным. Теснота связи между Z и Y (при постоянной X) оценивается вторым коэффициентом корреляции
.
Эти коэффициенты имеют те же свойства, что и обыкновенный выборочный коэффициент корреляции.
Пример 2
В таблице приведены результаты выборочного обследования двадцати семей по величине накопленных денежных средств Y (у.е.), суммарного дохода X1 (у.е.) и общей оценке имущества X2 (у.е.).
Y |
X1 |
X2 |
3 |
40 |
60 |
6 |
55 |
36 |
5 |
45 |
36 |
3,5 |
30 |
15 |
1,5 |
30 |
90 |
2 |
40 |
55 |
1 |
20 |
35 |
2,5 |
45 |
50 |
2,3 |
42 |
45 |
2,8 |
40 |
47 |
4 |
45 |
50 |
5 |
55 |
40 |
6 |
55 |
38 |
4,5 |
50 |
48 |
5 |
53 |
48 |
3,5 |
30 |
19 |
3,5 |
25 |
25 |
4 |
40 |
35 |
5 |
50 |
45 |
6 |
55 |
30 |
81
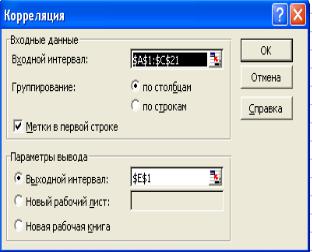
Необходимо:
1.Рассчитать и проанализировать матрицу парных коэффициентов корреляции.
2.Составить уравнение множественной регрессии У = f(X1, X2).
Решение
1.Заносим статистические данные на лист Excel в диапазон ячеек
А2:С21.
2.Вычислим матрицу парных коэффициентов корреляции. Для того необходимо:
–выполнить команду Сервис → Анализ данных → Корреляция→ ОК;
–в открывшемся диалоговом окне Корреляция зададим несколько параметров:
 в поле Входной интервал укажем диапазон с входными данными
в поле Входной интервал укажем диапазон с входными данными
А1:C21;
 в разделе Группирование поставим флажок по столбцам;
в разделе Группирование поставим флажок по столбцам;
 установим флажок Метки;
установим флажок Метки;
 установим переключатель в позицию Выходной интервал, укажем ячейку Е1.
установим переключатель в позицию Выходной интервал, укажем ячейку Е1.
– после задания всех необходимых параметров, щёлкаем по кнопке ОК – Excel выводит матрицу коэффициентов корреляции.
82
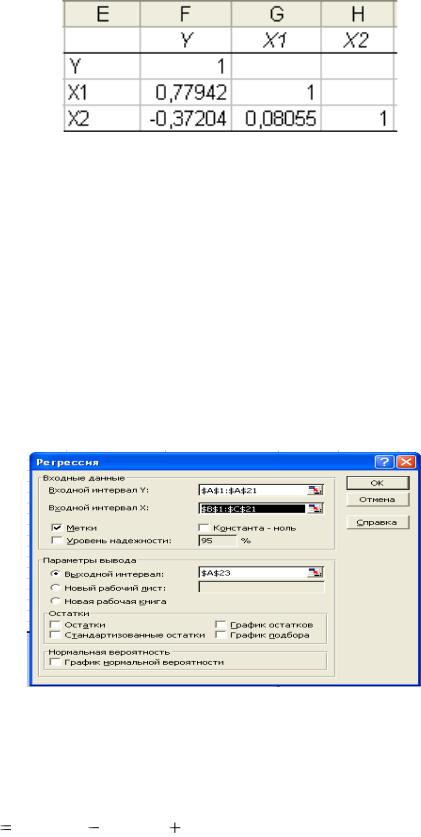
Вывод: |
|
|
|
|
Так как |
ryх = 0,779 и |
ryх |
2 |
= - 0,372, то связь между результирующим |
|
1 |
|
|
признаком Y и факторами X1 и X2 согласно шкале Чеддока оценивается как высокая и умеренная соответственно.
3.Составим уравнение множественной регрессии. Для этого:
–выполним команду Сервис → Анализ данных → Регрессия → ОК;
–в диалоговом окне Регрессия зададим несколько параметров по образцу:
После того, как необходимые параметры заданы, щёлкаем по кнопке
ОК. В полученном окне приведены коэффициенты уравнения множественной регрессии. Таким образом, искомое уравнение имеет вид: y 0,114  x1 0,04
x1 0,04  x2 0,692 .
x2 0,692 .
83
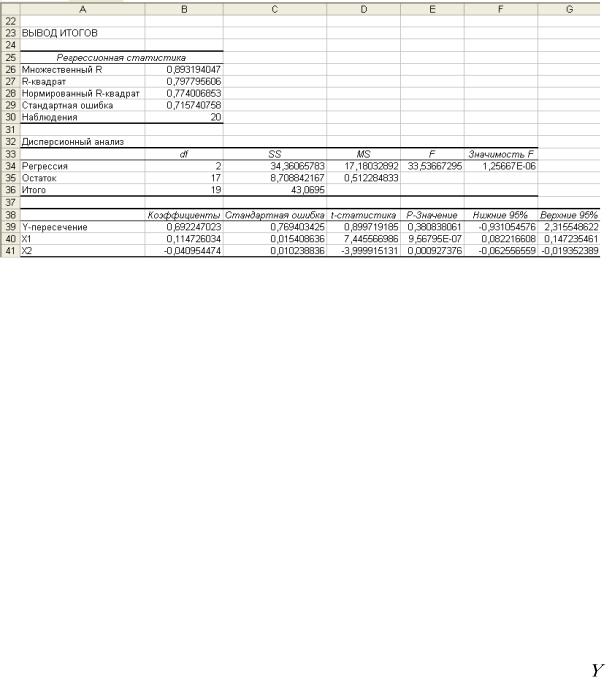
УПРАЖНЕНИЯ 1. В таблице приведены статистические данные о полугодовых
объёмах валового внутреннего продукта РФ (Y, млрд руб.) и соответствующих объемах суммарных инвестиций в основной капитал (I, млрд руб.), в реальном выражении.
Y |
152,99 |
166,50 |
131,25 |
158,73 |
132,69 |
149,00 |
131,97 |
148,82 |
115,87 |
I |
26,52 |
31,80 |
19,26 |
28,04 |
17,80 |
27,41 |
16,69 |
25,95 |
15,32 |
|
|
|
|
|
|
|
|
|
|
Y |
110,06 |
86,48 |
110,79 |
105,24 |
130,21 |
122,25 |
145,78 |
128,05 |
153,02 |
I |
17,52 |
8,31 |
15,48 |
14,02 |
27,96 |
17,61 |
29,54 |
16,11 |
26,54 |
|
|
|
|
|
|
|
|
|
|
Требуется:
а) оценить тесноту линейной корреляционной связи;
б) составить линейные уравнения регрессии  на I и I на , построить их графики.
на I и I на , построить их графики.
2. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей Х и стоимостью ежемесячного обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей.
Х |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
13 |
16 |
15 |
20 |
19 |
21 |
26 |
|
24 |
30 |
32 |
30 |
35 |
34 |
40 |
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
84 |
|
|
|
|
|
|
|
|
Требуется:
а) рассчитать выборочный коэффициент корреляции и проверить его значимость при α = 0,05; б) составить уравнение регрессии на Х и построить его график.
3. Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе города. Для этого он наугад выбирает 15 зданий, из имеющихся 1500 и получает следующие данные.
Общая |
Количество |
Количество |
Время |
Оценочная |
площадь |
офисов |
входов |
эксплуатации |
цена |
(Х1 ) |
(Х2) |
(Х3) |
(Х4) |
(Y) |
2310 |
2 |
2,0 |
20 |
142000 |
|
|
|
|
|
2333 |
2 |
2,0 |
12 |
144000 |
|
|
|
|
|
2356 |
3 |
1,5* |
33 |
151000 |
|
|
|
|
|
2379 |
3 |
2,0 |
43 |
150000 |
|
|
|
|
|
2402 |
2 |
3,0 |
53 |
139000 |
|
|
|
|
|
2425 |
4 |
2,0 |
23 |
169000 |
|
|
|
|
|
2448 |
2 |
1,5 |
99 |
126000 |
|
|
|
|
|
2471 |
2 |
2,0 |
34 |
142000 |
|
|
|
|
|
2494 |
3 |
3,0 |
23 |
169000 |
|
|
|
|
|
2517 |
4 |
4,0 |
55 |
149000 |
|
|
|
|
|
2540 |
2 |
3,0 |
22 |
158000 |
|
|
|
|
|
2563 |
3 |
2,0 |
33 |
166000 |
|
|
|
|
|
2586 |
4 |
3,0 |
66 |
150000 |
|
|
|
|
|
2609 |
2 |
1,5 |
14 |
161000 |
|
|
|
|
|
2632 |
2 |
5,0 |
5 |
163000 |
|
|
|
|
|
* "Полвхода" (1/2) означает вход только для доставки корреспонденции.
Составить уравнение множественной регрессии Y(X1, X2, X3, X4) для оценки цены офисного здания в заданном районе.
85
2.5. Дисперсионный анализ
Дисперсионный анализ (analysis of variance) – статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, а также для последующего планирования аналогичных экспериментов.
Дисперсионный анализ позволяет изучать зависимость изменения одной количественной переменной от изменения одной или нескольких независимых количественных или качественных переменных.
Зависимые переменные в дисперсионном анализе называются
результирующим признаком или откликом. Независимые переменные –
факторами.
Условия применения дисперсионного анализа в статистических исследованиях:
1.Генеральные совокупности, из которых формируются выборки, должны быть нормально распределены.
2.Выборки должны быть независимы.
3.Дисперсии генеральных совокупностей должны быть равны.
Однофакторный дисперсионный анализ (one-way analysis of
variance, One-Way ANOVA) – метод дисперсионного анализа, в котором изучается влияние единственного фактора на результирующий признак.
Пусть из генеральной совокупности отобрана выборка объёма nТ. Выборочные данные разбиты на k групп (число уровней фактора), по n наблюдений в каждой группе. Тогда математическая модель однофакторного дисперсионного анализа имеет вид
xij = μ + ai + εij , i (1, k) ,
где xij – j-е наблюдение в i-й группе; μ – общая генеральная средняя;
86
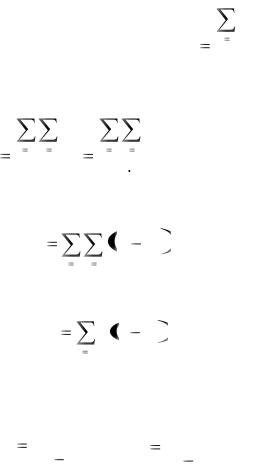
ai – отклонение средних в i-й группе от общей средней за счёт влияния фактора;
εij – случайные ошибки наблюдений.
Тогда однофакторный дисперсионный анализ позволяет проверить гипотезу о том, что влияние фактора на отклик отсутствует, т.е. Н0: а1 =
а2 = … = ак = 0.
Алгоритм однофакторного дисперсионного анализа
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xij |
|
1. |
Вычислить выборочную среднюю i-й группы |
xi |
j |
1 |
. |
|||||||||||||||||
|
|
|||||||||||||||||||||
|
n |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Вычислить общую выборочную среднюю |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
k |
n |
|
|
|
k |
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
xij |
|
|
|
xij |
|
|
|
|
|
|
|
|||
|
|
|
|
|
i 1 |
j |
1 |
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
||||
|
x |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
nT |
|
k |
n |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. |
Вычислить сумму квадратов внутригрупповых отклонений |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
n |
|
|
|
2 . |
|
|
|
|
|
||||
|
|
|
|
SSE |
|
|
|
xij |
|
xi |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|||
4. |
Вычислить сумму квадратов межгрупповых отклонений |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
2 . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
SSTR |
|
n xi |
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
||
5. |
Рассчитать средние квадраты, разделив SSE и SSTR на |
|||||||||||||||||||||
соответствующее число степеней свободы |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
MSE |
|
|
|
SSE |
, MSTR |
|
SSTR |
. |
|
|
|||||||||||
|
|
|
n |
k |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Рассчитать наблюдаемое значение критерия Фишера |
|
|
|||||||||||||||||||
|
|
|
|
|
Fнабл = |
|
MSTR |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
MSE |
|
|
|
|
|
|
|
|
|
|
||
7. Результаты вычислений представить в виде следующей таблицы:
87
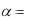
Источник |
Сумма |
Степени |
Средние |
F-статистика |
||
вариации |
квадратов |
свободы |
квадраты |
|
|
|
|
|
|
|
|
|
|
Межгрупповая |
SSTR |
df1=k – 1 |
MSTR |
F= |
MSTR |
|
|
|
|
|
MSE |
||
Внутригрупповая |
SSE |
df2=nT – k |
MSE |
|||
|
|
|
|
|
|
|
Общая |
SST |
df=nT – 1 |
|
|
|
|
|
|
|
|
|
|
|
8.По таблице значений критерия Фишера при заданном уровне значимости α найти критическое значение критерия Fкр=F(α, k–1, nT–k).
9.Сравнить Fнабл и Fкр. Если Fнабл< Fкр, следовательно, нет оснований отвергнуть нулевую гипотезу о равенстве средних, т.е. изменение
отклика не зависит изменения фактора. В противном случае нулевая гипотеза отвергается, т.е. результирующий признак зависит от изменения фактора модели.
Пример 1
В таблице приведены средние цены (у.е.) моделей легковых подержанных автомобилей, имеющих одинаковое техническое состояние, в пунктах продаж Москвы и Минска за восемь месяцев. Зависит ли средняя цена автомобиля от местонахождения пункта продаж (Минск, Москва)?
Мecяцы |
Стоимость модели, |
у.е. |
|
|
Минск |
|
Москва |
1 |
5 |
|
6,8 |
2 |
3,1 |
|
4,1 |
3 |
2,3 |
|
5 |
4 |
4,1 |
|
5,1 |
5 |
5,3 |
|
7,2 |
6 |
2,8 |
|
4,2 |
7 |
3,4 |
|
5,4 |
8 |
3,8 |
|
5,4 |
Решение
Предположим, что средняя цена автомобиля (отклик) не зависит от местонахождения пункта продаж (фактор). Выдвигаем нулевую гипотезу Н0: средние цены автомобилей в пунктах продаж Москвы и Минска совпадают. Проверим выдвинутую гипотезу при уровне значимости
0,05 согласно предложенному алгоритму.
88

1. Найдем выборочные средние в группах
|
|
|
|
5 |
3,1 ... |
3,8 |
|
|
6,8 |
4,1 |
... 5,4 |
|
|
|||||
x1 |
|
|
|
|
|
|
|
3,725 , |
x2 |
|
|
|
|
5,4. |
|
|||
|
8 |
|
|
|
|
|
8 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. Находим общую выборочную среднюю |
|
|
||||||||||||||||
|
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xij |
(5 ... |
3,8 6,8 ... |
5,4) |
|
|
|
|
||||||
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|||||||||
x |
|
4,56 . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
nT |
|
|
|
|
16 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Вычислим сумму квадратов внутригрупповых отклонений |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SSE |
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
5 3,725 2 ... |
3,8 |
3,725 2 |
6,8 |
5,4 2 |
... 5,4 5,4 2 |
16,215 . |
||||||||
4. Вычислим сумму квадратов межгрупповых отклонений |
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
SSTR |
n xi |
|
x |
8 3,7 |
4,56 2 |
5,4 |
4,56 2 |
11,222 . |
|
|||||||||
i1
5.Рассчитаем средние квадраты внутри и межгрупповых отклонений
MSE |
|
SSE |
16,215 |
1,158 , MSTR |
SSTR |
11,222 |
11,222 . |
|
|||
|
|
|
|
|
|
|
|
|
|||
|
nT k |
(16 2) |
k 1 |
(2 |
1) |
|
|||||
|
|
|
|
|
|||||||
6. |
Рассчитаем |
наблюдаемое |
значение |
|
критерия |
Фишера |
|||||
Fнабл= |
MSTR |
= |
11,222 |
9,689 . |
|
|
|
|
|
||
|
|
1,158 |
|
|
|
|
|
||||
|
MSE |
|
|
|
|
|
|
||||
7. Результаты вычислений представим в виде таблицы: |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||
Источник |
|
|
|
Сумма |
Степени |
Средние |
F-статистика |
||||
вариации |
|
|
|
квадратов |
свободы |
квадраты |
|
|
|
||
|
|
|
|
|
|
|
|
||||
Межгрупповая |
|
SSTR=11,21 |
k – 1=1 |
MSTR=11,22 |
F= |
MSTR |
9,66 |
||||
|
|
|
|
|
|
|
|
|
MSE |
||
Внутригрупповая |
|
SSE=16,23 |
nT k =14 |
MSE=1,158 |
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общая |
|
|
|
SST=27,44 |
nT –1=15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8. Найдём критическое значение критерия |
|
|
|
|
|||||||
|
|
|
|
Fкр=F(α, k–1, nT–k)=F(0,05; 1; 14)=4,6. |
|
|
|
||||
89
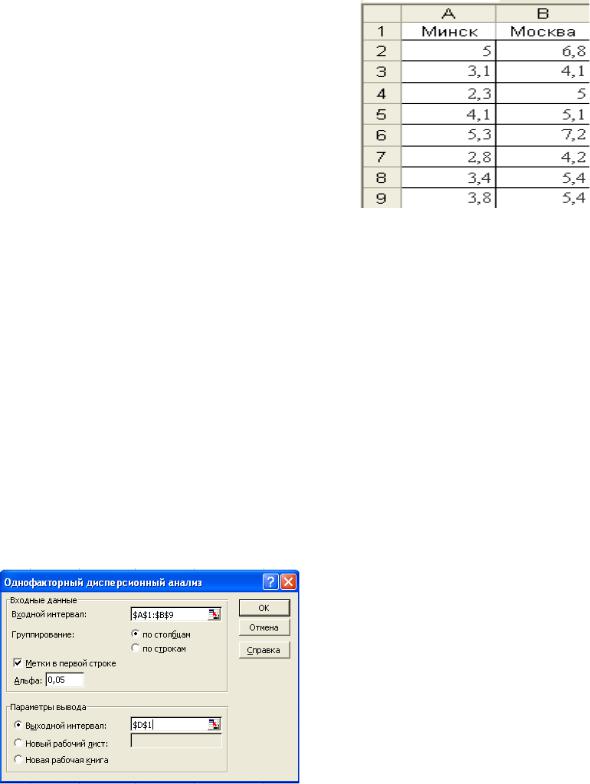
9. Так как Fнабл=9,66 > Fкр,=4,6, следовательно, нулевая гипотеза о равенстве средних отклоняется. Таким образом, средняя стоимость автомашин зависит от местонахождения пункта продаж.
Рассмотрим решение данной задачи средствами Excel.
1.Заносим статистические данные на лист Excel, как показано на рисунке.
2.Надстройка Пакет анализа
содержит инструмент Однофакторный дисперсионный анализ, с помощью которого Еxcel производит выполнение однофакторного дисперсионного анализа.
Для того чтобы запустить в работу инструмент Однофакторный дисперсионный анализ, необходимо:
–выполнить команду Сервис → Анализ данных (если надстройка Пакет анализа не подключена → выполнить команду Сервис → Надстройки → установить флажок в поле Пакет анализа, затем команду Сервис → Анализ данных);
–в открывшемся диалоговом окне Анализ данных выберем инструмент
Однофакторный дисперсионный анализ → ОК;
–в открывшемся диалоговом окне определим несколько параметров:
 в поле Входной интервал
в поле Входной интервал
укажем диапазон с входными данными А1:В9;
 в разделе Группирование
в разделе Группирование
установим флажок по столбцам, так как изначально
90

исходные данные введены в столбцы А и В (флажок по строкам устанавливают в случае расположения исходных данных в строках);  в поле Альфа введите уровень значимости (в нашем случае 0,05);
в поле Альфа введите уровень значимости (в нашем случае 0,05);
 флажок Метки устанавливают, если первая строка исходного диапазона содержит название полей – в нашем случае − да;
флажок Метки устанавливают, если первая строка исходного диапазона содержит название полей – в нашем случае − да;  с помощью переключателя Параметры вывода, определим, куда
с помощью переключателя Параметры вывода, определим, куда
должны быть помещены выходные данные – установим переключатель в позицию Выходной интервал, в поле укажем ячейку D1;
– после того, как все необходимые параметры заданы, щелкаем по кнопке ОК – Excel выводит все расчёты по однофакторному дисперсионному анализу.
3. Таблица дисперсионного анализа содержит все расчёты, произведённые нами вручную. В графе Итоги приведены общие описательные статистики по каждой группе: число элементов в группе (Счёт), сумма элементов в группе (Сумма), среднее значение и дисперсия в каждой группы (Среднее, Дисперсия).
Выводы:
1. Наблюдаемое значение критерия Фишера Fнабл=9,689 (ячейка Н11) больше критического значения Fкр=4,6 (ячейке J11), следовательно, гипотеза о независимости средней цены автомобиля от пункта продаж отвергается.
91
2. Р-значение в ячейке I11 составляет 0,007 и не превышает заданного уровня значимости α = 0,05, следовательно, гипотеза о равенстве средних отклоняется. Таким образом, средняя стоимость автомашин зависит от местонахождения пункта продаж.
Двухфакторный дисперсионный анализ (two-way analysis of variance, Two-Way ANOVA) – модель дисперсионного анализа, которая описывает влияние двух факторов, а также эффект взаимодействия этих факторов на исследуемый показатель.
Математическая модель линейного двухфакторного дисперсионного анализа имеет вид:
xijk =μ+ai+bj+ (ab)ij+εijk, , |
|
|
|
|
где xijk – значение изучаемого признака; |
|
|
|
|
μ – генеральная средняя; |
|
|
|
|
|
|
|
|
|
аi – эффект, обусловленный влиянием i-го уровня фактора А, i |
(1, I ) ; |
|||
|
|
|
|
|
bj – эффект, обусловленный влиянием j-го уровня фактора B, j |
(1, J ) ; |
|||
(ab)ij – эффект, обусловленный взаимодействием двух факторов А и В;
εijk – возмущение, обусловленное влиянием неучтённых факторов.
92
Тогда двухфакторный дисперсионный анализ позволяет проверить три гипотезы:
H0A : все аi = 0, т.е. влияние фактора А на отклик отсутствует;
H0B : все bj = 0, т.е. влияние фактора B на отклик отсутствует;
H0AB : все (аb)ij = 0, т.е. пересечение факторов (их совместное влияние на отклик) отсутствует.
Отклонение какой-либо из этих гипотез означает, что изменение результирующего показателя обусловлено влиянием соответствующего фактора.
Таким образом, в случае двухфакторного дисперсионного анализа полная дисперсия, обуславливающая изменчивость признака в серии опытов, раскладывается на составляющие её дисперсии, обусловленные варьированием факторов, ошибкой эксперимента и действием неучтённых факторов. Изменчивость в двухфакторном анализе можно представить в виде следующей схемы.
SST=SSA+SSB+SSAB+SSE
Алгоритм двухфакторного дисперсионного анализа
1. Вычислить средние выборочные в группах i и j
|
xijk |
|
xijk |
|
|
xi |
j, k |
; x j |
i,k |
. |
|
JK |
IK |
||||
|
|
|
93
|
|
|
|
|
|
|
|
|
|
|
|
|
xijk |
|
|
|
|
||||
2. |
Вычислить общую выборочную среднюю |
x |
|
i, j,k |
|
|
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
IJK |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xijk |
|
|
|
|
3. |
Вычислить выборочные средние k-й группы |
xij |
k |
1 |
; |
|
|
|
|||||||||||||
|
K |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Вычислить суммы квадратов отклонений: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
I |
|
|
x 2 , SSB |
|
J |
|
x 2 , |
|
|
|
|
|||||
|
|
|
SSA |
JK |
xi |
IK |
|
x j |
|
|
|
|
|
||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
||
|
|
SSAB K |
|
xij |
x |
xi x j |
2 , SSE |
|
|
|
xijk xij |
2 . |
|
||||||||
|
|
|
|
i, j |
|
|
|
|
|
|
|
i, j,k |
|
|
|
|
|
|
|
||
5. |
Рассчитать средние квадраты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
MSA |
SSA |
; MSВ |
|
SSB |
|
; |
MSAB |
|
|
SSAB |
; |
|
MSE |
|
SSE |
; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(I 1) |
|
(J 1) |
|
|
I 1 (J 1) |
|
|
|
|
|
IJ K 1 |
|
|||||||
6. Наблюдаемые значения критерия Фишера определяем по формулам:
FнаблА = MSAMSE , FнаблВ = MSBMSE , FнаблАВ = MSABMSE .
7. Результаты вычислений представить в виде следующей таблицы
Источник |
Сумма |
|
Степени |
Средние |
|
F-статистика |
вариации |
квадратов |
|
свободы |
квадраты |
|
|
Главные эффекты |
SSA+SSB |
|
I–1+J–1 |
MSA+MSB |
|
|
Фактор A |
SSA |
|
I–1 |
MSA |
|
FA |
Фактор В |
SSB |
|
J–1 |
MSB |
|
FB |
Эффект |
SSAB |
|
(I–1)(J–1) |
MSAB |
|
FAB |
пересечения |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ошибки |
SSE |
|
IJ (K–1) |
MSE |
|
FЕ |
Итого |
SST |
|
IJK–1 |
|
|
|
8. По таблице |
значений |
критерия Фишера находим |
критические |
|||
значения критерия
94

F А =F(α, I–1, IJ∙(K–1)), |
F В =F(α, J–1, IJ∙(K–1)), |
кр |
кр |
FкрАВ =F(α, (I–1)∙(J–1), IJ∙(K–1)).
9.Сравнить Fнабл и Fкр:
▪если FнаблА < FкрА , то нет оснований отвергнуть нулевую гипотезу H0A , следовательно, все средние, образованные за счёт фактора А равны;
▪если FнаблВ < FкрВ , то нет оснований отвергнуть нулевую гипотезу H0B , следовательно, все средние, образованные за счёт фактора В равны;
▪если FнаблАВ < FкрАВ , то нет оснований отвергнуть нулевую гипотезу
H0AB , следовательно, все средние, образованные за счёт фактора А равны.
Пример 2
Рекламная компания в целях исследования эффективности своей рекламы размещает два рекламных ролика: один на косметическую продукцию, второй на спортивные товары на телевидении в рабочие и выходные дни. Случайным образом отбираются 16 потенциальных клиентов и делятся на 4 группы. После просмотра ролика каждого покупателя просят оценить эффективность рекламы по двадцатибалльной шкале. В таблице приведены баллы, выставленные каждым клиентом.
Реклама |
Рабочий день |
Выходной день |
Спортивные |
6 |
15 |
товары |
10 |
18 |
|
11 |
14 |
|
9 |
16 |
Косметическая |
8 |
19 |
продукция |
|
|
|
13 |
20 |
|
12 |
13 |
|
10 |
17 |
95

Необходимо выяснить, влияет ли вид рекламируемой продукции и тип дня просмотра рекламы, а также эффект взаимодействия между этими двумя переменными на оценки потенциальных покупателей.
Решение
Предположим, что эффективность рекламы (отклик) не зависит ни от вида рекламируемой продукции (фактор А), ни от дня просмотра рекламы (фактор В), ни от совместного влияния этих факторов.
Выдвигаем нулевые гипотезы:
H0A : эффективность рекламы не зависит от вида продукции;
H0B : эффективность рекламы не зависит от дня просмотра;
 H0AB : совместное влияния факторов на эффективность рекламы отсутствует.
H0AB : совместное влияния факторов на эффективность рекламы отсутствует.
Проверим выдвинутые гипотезы при уровне значимости 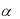 0,05 согласно предложенному алгоритму.
0,05 согласно предложенному алгоритму.
Фактор А (вид рекламируемой продукции) имеет два уровня (I=2). Фактор В (день показа видеоролика) имеет также два уровня (J=2). Каждая группа опрошенных включает четыре потенциальных клиента (К=4).
1. Находим выборочные средние i-й группы по формулам:
|
|
x1 jk |
6 10 11 9 15 18 14 16 |
|
|
|
|||
xi 1 |
j, k |
12,375 |
, |
||||||
|
|
|
|
|
|
||||
|
JK |
2 4 |
|||||||
|
|
|
|
|
|||||
|
|
x2 jk |
8 13 12 10 19 20 13 17 |
|
|
||||
xi 2 |
|
j, k |
14 . |
|
|||||
|
|
|
|
|
|
|
|
||
|
JK |
2 4 |
|
|
|||||
|
|
|
|
|
|||||
Находим выборочные средние j-й группы по формулам:
96

|
|
xi1k |
6 |
10 |
11 |
9 8 13 12 10 |
|
|
|
|||
x j 1 |
|
i, k |
|
9,875 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
IK |
|
|
|
|
|
2 4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
xi 2k |
15 |
18 |
14 |
16 19 20 13 17 |
|
|
||||
x j 2 |
i, k |
16,5 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
IK |
|
|
|
|
|
2 4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
2. Находим общую выборочную среднюю
|
xijk |
6 10 11 ... 20 13 17 |
|
||
x |
i, j,k |
13,1875 . |
|||
|
|
|
|||
IJK |
2 2 4 |
||||
|
|
||||
3. Находим выборочные средние k-й группы по формулам:
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x11k |
6 |
10 |
11 |
9 |
|
|
x12k |
15 |
18 |
14 |
16 |
|
|
|
|||||
|
x11 |
|
k 1 |
9 , x12 |
k 1 |
|
|
15,75 , |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
K |
|
|
4 |
|
|
|
K |
|
|
|
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x21k |
8 |
13 |
12 |
10 |
|
|
|
x22k |
|
|
19 |
20 |
13 |
17 |
|
||||||
x21 |
k 1 |
|
|
|
10,75 , x22 |
|
k 1 |
|
|
17,25 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
K |
|
|
|
|
4 |
|
|
|
K |
|
|
|
|
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. Вычислим суммы квадратов отклонений:
SSA |
JK |
xi |
x 2 |
2 |
4 (12,375 |
13,1875)2 |
14 13,1875 2 |
10,5625 , |
||
|
|
i |
|
|
|
|
|
|
|
|
SSB |
IK |
x j |
x 2 |
2 |
4 |
(9,875 |
13,1875)2 |
(16,5 13,1875)2 |
175,5625, |
|
|
|
j |
|
|
|
|
|
|
|
|
SSAB |
K |
x |
x |
x |
x |
2 |
|
|
|
|
|
|
ij |
|
i |
|
j |
|
|
|
|
|
|
i, j |
|
|
|
|
|
|
|
|
4 |
9 13,1875 |
12,375 |
|
9,875 2 |
... 17,25 |
13,1875 14 16,5 2 |
0,0625, |
|||
97

SSE |
x |
x |
2 |
( 6 |
9 2 ... |
(15 15,75)2 ... (8 10,75)2 ... |
|
ijk |
ij |
|
|
|
|
|
i, j, k |
|
|
|
|
|
(19 |
17,25)2 |
... |
(17 |
17,25)2 ) |
66,25. |
|
5. Рассчитаем средние квадраты, разделив SSА, SSB, SSAB и SSE на соответствующее число степеней свободы:
MSA |
SSA |
10,5625 |
10,5625, |
|
MSВ |
|
SSB |
175,5625 |
175,5625 |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
(I 1) |
2 1 |
|
|
(J |
1) |
2 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
MSAB |
|
|
SSAB |
0,0625 |
|
|
0,0625 , |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
I 1 (J 1) |
(2 1) |
(2 |
1) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
MSE |
|
SSE |
66,25 |
|
|
5,52 . |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
IJ K 1 |
2 2 |
4 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. Наблюдаемые значения критерия Фишера определяем по формулам:
|
F А |
= |
MSA |
=10,5625/5,52=1,913, |
F В |
= |
MSB |
=175,5625/5,52=31,8, |
||||||||
|
|
|||||||||||||||
|
набл |
|
MSE |
|
|
|
|
|
|
набл |
|
|
MSE |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
F АВ |
= |
MSAB |
=0,0625/5,52=0,011. |
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
набл |
|
MSE |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. Результаты вычислений представим в виде следующей таблицы: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Источник |
|
Сумма |
Степени |
|
|
Средние |
|
F-статистика |
|||||||
|
вариации |
|
квадратов |
свободы |
|
|
квадраты |
|
|
|||||||
|
Гл. эффекты |
|
SSA+SSB |
I–1+J–1=2 |
|
|
MSA+MSB |
|
FA+B |
|||||||
|
Фактор A |
|
SSA=10,5625 |
|
I–1=1 |
|
|
MSA=10,56 |
|
FA = 1,913 |
||||||
|
Фактор В |
|
SSB=175,562 |
|
J–1=1 |
|
|
MSB=175,56 |
|
FВ = 31,8 |
||||||
|
Эффект |
|
SSAB=0,0625 |
(I–1)(J–1)=1 |
|
|
MSAB=0,062 |
|
FAВ = 0,011 |
|||||||
|
пересечения |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ошибки |
|
SSE=66,25 |
IJ (K–1)=12 |
|
|
MSE=5,52 |
|
|
|||||||
|
Итого |
|
SST= 252,437 |
IJK–1=15 |
|
|
|
|
|
|
||||||
8. По |
таблице значений |
критерия Фишера находим |
критические |
|||||||||||||
значения критерия: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
FкрА =F(α, I–1, IJ∙(K–1)) = F(0,05;1;12)=4,74, |
|
|||||||||||
|
|
|
|
FкрВ =F(α, J–1, IJ∙(K–1)) = F(0,05;1;12)= 4,74, |
|
|||||||||||
98
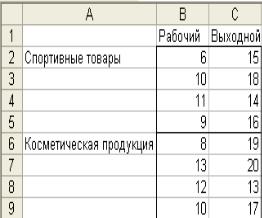
FкрАВ =F(α, (I–1)∙(J–1), IJ∙(K–1)) = F(0,05;1;12)=4,74.
9.Сравниваем Fнабл и Fкр:
▪т.к. FнаблА < FкрА , то нет оснований отвергнуть нулевую гипотезу H0A , следовательно эффективность рекламы не зависит от вида рекламируемой продукции;
▪т.к. FнаблВ > FкрВ , то нулевую гипотезу H0B отвергаем, следовательно,
эффективность рекламы зависит от дня её демонстрации;
▪ т.к. FнаблАВ < FкрАВ , то нет оснований отвергнуть нулевую гипотезу H0AB , следовательно, совместное влияния факторов на эффективность рекламы отсутствует.
Рассмотрим решение данной задачи средствами Excel.
1. Заносим статистические данные на лист Excel, как показано на рисунке.
2. Надстройка Пакет анализа
содержит |
инструмент |
Двухфакторный дисперсионный
анализ.
Для того чтобы запустить в работу инструмент Двухфакторный дисперсионный анализ, необходимо:
–выполнить команду Сервис → Анализ данных;
–в открывшемся диалоговом окне Анализ данных выберем инструмент
Двухфакторный дисперсионный анализ → ОК;
–в открывшемся диалоговом окне Двухфакторный дисперсионный анализ
определим несколько параметров:
99
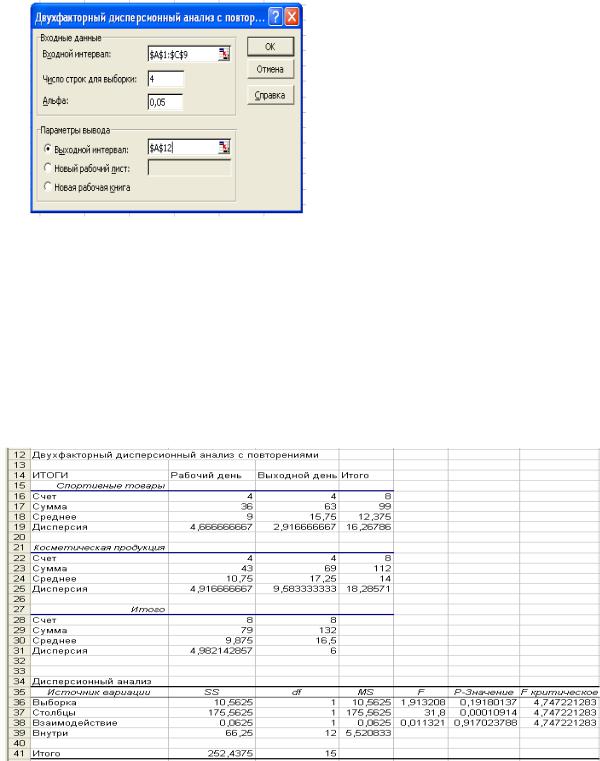
 в поле Входной интервал
в поле Входной интервал
укажем диапазон с входными
данными А1:С9;
 в поле Число строк для выборки введем число
в поле Число строк для выборки введем число
объектов в каждой подгруппе
(в нашем случае клиентов 4);
 в поле Альфа введите уровень значимости (в нашем случае 0,05);
в поле Альфа введите уровень значимости (в нашем случае 0,05);
 с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим
с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим
переключатель в позицию Выходной интервал, в соответствующем
поле укажем ячейку А12;
– после того как все необходимые параметры заданы, нажимаем ОК.
Выводы:
1. Сравнивая полученные наблюдаемые и критические значения критериев Фишера, делаем заключение о том, что эффективность рекламы зависит от дня её демонстрации и не зависит от прочих приведённых факторов.
100

2. Р-значения: рА = 0,191> α=0,05 , рВ = 0,0001< α=0,05 и рАВ = 0,917>
α=0,05 свидетельствуют о том, что нулевые гипотезы H0A и H0AB не отклоняются и гипотезу H0B следует отклонить.
УПРАЖНЕНИЯ
1. Автомобильная компания имеет тридцать два торговых представительства по продажам своих автомобилей. Каждое из них работает согласно выбранному плану:
 План А – работа с клиентами через интернет-магазин;
План А – работа с клиентами через интернет-магазин;
 План В – продажа автомобилей в элитных автосалонах города;
План В – продажа автомобилей в элитных автосалонах города;
 План C – поиск покупателей по объявлениям в газете;
План C – поиск покупателей по объявлениям в газете;  План Г – торговля через банк в кредит.
План Г – торговля через банк в кредит.
Продажи автомобилей, (у.е.)
План А |
План В |
План С |
План Г |
360 |
390 |
440 |
310 |
400 |
450 |
430 |
430 |
320 |
540 |
380 |
460 |
440 |
530 |
400 |
430 |
350 |
460 |
410 |
360 |
410 |
420 |
350 |
490 |
440 |
350 |
370 |
460 |
420 |
390 |
370 |
480 |
Выяснить, оказывает ли влияние план работы представительства на уровень продаж.
2. В таблице приведены данные о месторасположении гостиниц города и степени заполняемости их в определённый период времени. Необходимо выяснить, влияет ли расстояние от центра города на степень заполняемости гостиниц.
Расстояние |
|
|
Заполняемость, % |
|
|
|||
|
|
|
|
|
|
|
|
|
до 3 км |
92 |
98 |
|
89 |
97 |
|
90 |
94 |
|
|
|
|
|
|
|
|
|
от 3 до 5 км |
90 |
86 |
|
84 |
91 |
|
83 |
82 |
|
|
|
|
|
|
|
|
|
свыше 5 км |
87 |
79 |
|
79 |
85 |
|
73 |
77 |
|
|
|
|
|
|
|
|
|
101
Библиографический список
1.Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. – М. : ЮНИТИ, 1998.
2.Гельман В. Я. Практикум по математике на компьютере. − СПб. :
СПИГ, 2001.
3.Гмурман В. Е. Теория вероятностей и математическая статистика. 
М. : Высшая школа, 2001.
4.Додж М., Стинсон К. Эффективная работа: Microsoft Excel 2002. −
СПб. : Питер, 2003.
5.Ежова Л. Н. Эконометрика. Начальный курс с основами теории вероятностей и математической статистики : учеб. пособие. –
Иркутск : Изд-во БГУЭП, 2002.
6.Колемаев В. А., Калинина В. Н. Теория вероятностей и математическая статистика : учебник. – М. : ЮНИТИ - ДАНА, 2003.
7.Кремер Н. Ш. Теория вероятностей и математическая статистика. –
М. : ЮНИТИ, 2000.
8.Пикуза В., Геращенко А. Экономические и финансовые расчёты в
Excel : самоучитель. − СПб. : Питер, 2002.
9.Эддоус М., Стэнсфилд Р. Методы принятия решений. М. : Аудит,
ЮНИТИ, 1997.
10.Экономическая информатика / ред. П. В. Конюховский, Д. Н.
Колесов. − CПб . : Питер, 2000.
11.Keller, Gerald, Brian Warrack, and Henry Bartel. Statistics for Management and Economics. 3rd ed. Belmont, Calif.: Duxbury, 1994.
12.Mendenhall, William, James E. Reinmuth, and Robert J. Beaver. Statistics for Management and Economics. 7th ed. Belmont, Calif.: Duxbury, 1993.
13.Menzefricke, Ulrich. Statistics for Managers. Belmont, Calif.: Duxbury,
1995.
102
ПРИЛОЖЕНИЕ
|
|
Критические точки распределения |
2 |
|
|||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
Уровень значимости α |
|
|
|||
степеней |
0,01 |
|
0,025 |
|
0,05 |
0,95 |
|
0,975 |
0,99 |
свободы |
|
|
|
|
|
|
|
|
|
1 |
6,6 |
|
5,0 |
|
3,8 |
0,039 |
|
0,00098 |
0,00016 |
2 |
9,2 |
|
7,4 |
|
6,0 |
0,103 |
|
0,051 |
0,020 |
3 |
11,3 |
|
9,4 |
|
7,8 |
0,352 |
|
0,216 |
0,115 |
4 |
13,3 |
|
11,1 |
|
9,5 |
0,711 |
|
0,484 |
0,297 |
5 |
15,1 |
|
12,8 |
|
11,1 |
1,15 |
|
0,31 |
0,554 |
6 |
16,8 |
|
14,4 |
|
12,6 |
1,64 |
|
1,24 |
0,872 |
7 |
18,5 |
|
16,0 |
|
14,1 |
2,17 |
|
1,69 |
1,24 |
8 |
20,1 |
|
17,5 |
|
15,5 |
2,73 |
|
2,18 |
1,65 |
9 |
21,7 |
|
19,0 |
|
16,9 |
3,33 |
|
2,70 |
2,09 |
10 |
23,2 |
|
20,5 |
|
18,3 |
3,94 |
|
3,25 |
2,56 |
11 |
24,7 |
|
21,9 |
|
19,7 |
4,57 |
|
3,82 |
3,05 |
12 |
26,2 |
|
23,3 |
|
21,0 |
5,23 |
|
4,40 |
3,57 |
13 |
27,7 |
|
24,7 |
|
22,4 |
5,89 |
|
5,01 |
4,11 |
14 |
29,1 |
|
26,1 |
|
23,7 |
6,57 |
|
5,63 |
4,66 |
15 |
30,6 |
|
27,5 |
|
25,0 |
4,26 |
|
6,26 |
5,23 |
16 |
32,0 |
|
28,8 |
|
26,3 |
7,96 |
|
6,91 |
5,81 |
17 |
33,4 |
|
30,2 |
|
27,6 |
8,67 |
|
7,56 |
6,41 |
18 |
34,8 |
|
31,5 |
|
28,9 |
9,39 |
|
8,23 |
7,01 |
19 |
36,2 |
|
32,9 |
|
30,1 |
10,1 |
|
8,91 |
7,63 |
20 |
37,6 |
|
34,2 |
|
31,4 |
10,9 |
|
9,59 |
8,26 |
21 |
38,9 |
|
35,5 |
|
32,7 |
11,6 |
|
10,3 |
8,90 |
22 |
40,3 |
|
36,8 |
|
33,9 |
12,3 |
|
11,0 |
9,54 |
23 |
41,6 |
|
38,1 |
|
35,2 |
13,1 |
|
11,7 |
10,2 |
24 |
43,0 |
|
39,4 |
|
36,4 |
13,8 |
|
12,4 |
10,9 |
25 |
44,3 |
|
40,6 |
|
37,7 |
14,6 |
|
13,1 |
11,5 |
26 |
45,6 |
|
41,9 |
|
38,9 |
15,4 |
|
13,8 |
12,2 |
27 |
47,0 |
|
43,2 |
|
40,1 |
16,2 |
|
14,6 |
12,9 |
28 |
48,3 |
|
44,5 |
|
41,3 |
16,9 |
|
15,3 |
13,6 |
29 |
49,6 |
|
45,7 |
|
42,6 |
17,7 |
|
16,0 |
14,3 |
30 |
50,9 |
|
47,0 |
|
43,8 |
18,5 |
|
16,8 |
15,0 |
103
