5571

ОГЛАВЛЕНИЕ

Введение

1.Простые проценты

2.Сложные проценты

3.Сила процента

4.Учет инфляции и налогообложения

5.Потоки наличности

6.Ренты

7.Уравнение стоимости

8.Варианты контрольных работ

9.Библиографический список

2

ВВЕДЕНИЕ

Внастоящее время при переходе к рыночной экономике все возрастающую роль в экономической жизни государства играет страховое дело. В странах с развитой экономикой западного типа страхование давно переросло рамки обычного дела, бизнеса и

кнастоящему времени представляет собой основу инфраструктуры, главный стабилизирующий фактор экономики. Действительно, страхование и перестрахование как отдельных граждан так и всевозможных структурных единиц банковского дела и бизнеса приводит к абсолютному выравниванию риска между всеми членами общества и, следовательно, к исчезновению в конечном счете риска как такого.

Существенную роль в страховом деле, финансах и бизнесе играют актуарии. Традиционно актуарии вовлекались главным образом в сферу страхования жизни и пенсий. В этих сферах присутствует долговременная перспектива, инвестиции играют главную роль, природа финансовых рисков такова, что математические модели могут дать о них ценные сведения. Благодаря глубокому пониманию финансовых механизмов страхования, актуарии играют доминирующую роль в управлении страховыми компаниями.

Актуарии также активно действуют в области финансов и инвестиций, будь то управление инвестиционным портфелем, исследование и дублирование управления фондами и брокерами фондовой биржи, измерение и мониторинг инвестиционного исполнения, управление взаимосвязью между доходами и расходами или анализ современных финансовых инструментов.

Актуарии применяются в других областях, таких как персональное финансовое планирование, оценка персонального ущерба (включая потерю дохода или пенсионных прав) в случае судебных процессов, экспертиза планов размещения капитала, корпоративное планирование, оценка промышленных рисков и управление.

Актуарная наука состоит из трех основных разделов:

1. Финансовая математика или теория процентных ставок.

2. Демографическое прогнозирование.

3. Оценка рисков.

Впервой части настоящего пособия (темы 1-7) будут исследоваться методы исчисления процентов и расчеты, связанные с простыми, сложными и непрерывными процентными ставками. Будут рассматриваться задачи как для отдельных разовых платежей, так и их последовательностей (потоков наличности, финансовых рент).

Во второй части пособия (темы 8-11) будут рассмотрены методология построения тарифов, а также методики ценообразования в страховании жизни, в пенсионном страховании и массовых рисковых видах страхований. Завершится пособие обсуждением методов оценки и управления предпринимательскими рисками.

1.ПРОСТЫЕ ПРОЦЕНТЫ

3

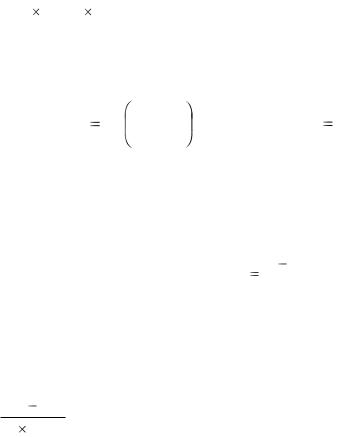
следующих соображения.

Во-первых, в схеме простых процентов происходит непрерывное накопление капитала, тоесть величина t в формуле (1.3) может принимать любые положительные значения (не обязательно целые).

Во-вторых, величины i и t должны быть представлены в одних и тех же единицах: если процентная ставка измеряется в единицах 1 в год, то единица времени - год, если берется квартальная процентная ставка, то время измеряется в кварталах и т.д.

Пример 1.1. Найти сумму простых процентов по кредиту в 500£ на 75 дней при i~8,5% в год.

Решение. Так как дана годовая процентная ставка, то время необходимо измерить в годах, то есть t = 75/365 лет. Тогда по формуле (1.2) сумма простых процентов равна:

5 = 500 0,085 75/365 = 8,73£

Иногда полезно переводить процентные ставки из одной единицы измерения в другую. Для этого достаточно сделать переход к другим единицам измерения времени. Так, например, если дана годовая процентная ставка i (1/год), то месячная процентная

Если дана, например, квартальная ставка i(1/квартал), то годовая равна: i1 = i(1:1/4года) = 4i (1/год).

В некоторых задачах требуется найти процентную ставку. Для этого достаточно воспользоваться формулой (1.3)

Пример 1.2. В погашение кредита в 200£ через месяц должно быть уплачено 210£. Найти простую процентную ставку в год.

Решение.

Здесь А = 210£, Р - 200£, t.= 1месяц. Пользуясь формулой (1.4), получим.

i= 210 200 = 0,05.

1 200

Исходя из указанных единиц измерения i - это месячная процентная ставка, то есть i =

0,05 (1/месяц)

Тогда годовая процентная ставка

1.3.Текущая стоимость

Впредыдущем разделе мы искали накопленную стоимость начального капитала при простых процентах. Рассмотрим обратную задачу: найти начальную стоимость Р по известному накопленному капиталу А. Из формулы (1-3) находим

5

В формуле (1.5) начальный капитал Р носит название текущей стоимости капитала А. Нетрудно заметить, что текущая стоимость зависит от процентной ставки и от периода времени.

Пример 1.3. Найти текущую стоимость суммы 600£, уплачиваемой через 4,5 года, при простой процентной ставке 1) 12 % в год, 2) 3 % в полугодие.

Решение.

Пример 1.4. Требуются суммы 350£ и 500£ соответственно через 3 и 5 лет. Требуется найти сумму, которую следует инвестировать для получения этих сумм. Предполагается, что процентная ставка равна 7 % в год.

Решение: Обозначим через Р искомую сумму. Пусть А1 = 350£, A2 = 500£, t1 = 3, t2 = 5, i = 0,07. Рассмотрим два варианта решения.

1. Через t1 лет инвестированная сумма даст накопленную стоимость

Решая уравнение (1.6), найдем

( ₤ ).

Два различных способа приводят к разным результатам. Какой из способов ошибочен?

6

Ошибочность первого способа заключается в том, что мы вышли за рамки простых процентов. На втором этапе были взяты проценты от процентов, то есть были использованы сложные проценты. Для того чтобы, оставаться в рамках простых процентов, уравнение (1.6) нужно изменить, а именно:

Решая это уравнение, получи

Первый способ решения задачи, приводящий к уравнению (1.6), соответствует реальной ситуации, когда через 3 года счет закрывается, и сразу же открывается новый.

1.4. Простой дисконт

Примep 1.5. Пусть за 3 года начальный капитал 1000£ вырос до 1300£. Найдем простую годовую процентную ставку

В процентном исчислении простая годовая процентная ставка равна 10 %. Рассмотрим процентную ставку нового типа, когда прирост капитала учитывается как доля от накопленной суммы. В этом случае мы придем к так называемой простой дисконтной или учетной ставке (сокращенно простой дисконт). Обозначим простой дисконт символом

d, тогда, по определению,

где А - накопленный капитал; Р - начальный капитал. В данном случае мы называем Р текущей или дисконтированной стоимостью капитала А, и А - накопленной стоимостью капитала Р. В данном примере

d = 1300 1000 = 0, 077. 3 1300

то есть годовая учетная ставка равна 7, 7 %.

Найдем соотношение между учетной и процентной ставками. Из формулы (1.8) следует:

7

Экономический смысл равенства (1.10) состоит в том, что учетную ставку можно рассматривать как текущую стоимость процентной ставки, то есть дисконт - это процент уплачиваемый вперед.

Пример 1.6. Дисконтировать 900£ за 7 месяцев при простой процентной ставке 10 % в год.

Решение. Найдем текущую стоимость суммы 900£:

Пример 1.7. Дисконтировать 600£ за 4 месяца при учетной ставке 9% в год. Найти процентную ставку.

то есть годовая процентная ставка равна 9,3 %.

Примером применения простых процентов служат долговые обязательства, то есть письменные обязательства уплатить указанную сумму в указанный срок.

Пример 1.8. Обязательство

Пусть это обязательство продается до срока платежа 2 октября 1987 г. и дисконтируется по учетной ставке 9,5% в год. Определить

1)цену продажи,

2)норму прибыли г-на А,

3)норму прибыли банка,

4)дату продажи с оптимальной нормой прибыли г-на А,

5)дату покупки с оптимальной нормой прибыли банка.

Решение. При сроке погашения обязательства t = 60 дней от времени продажи до срока платежа 31 октября остается t1 = 29 дней.

Номинальная стоимость Р0 = 2000£, процентная ставка i = 0,11, фактическая

8

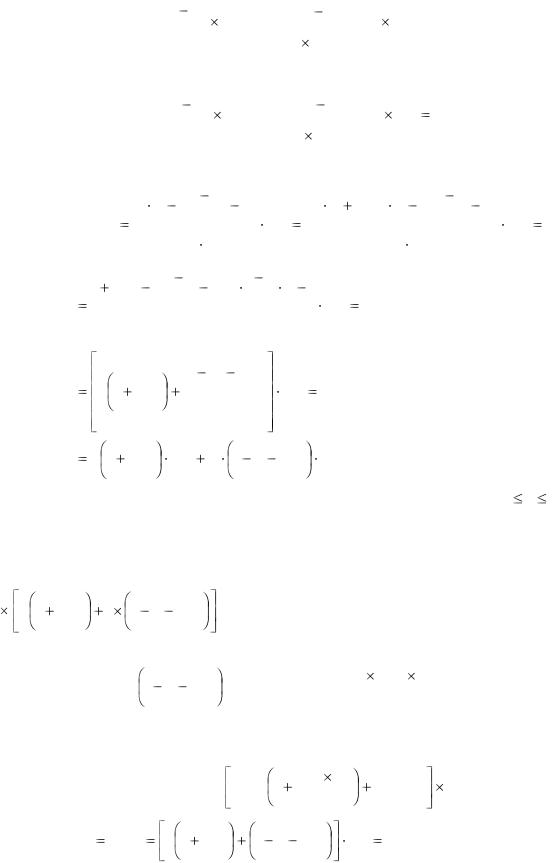
2. Норма прибыли г-на А:

Вывод: ценную бумагу в данном случае выгоднее продать сразу после заключения сделки, так как норма прибыли к концу срока уменьшается в 8 раз.

9

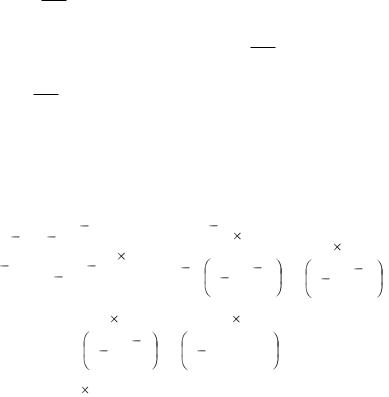
2.Пусть i – d – 365idt = 0 .

Вэтом случае СА(х) постоянна: СА (х) = d(1+ 365it ) .

3.Пусть i –d – 365idt = 0

В этом случае СA(X) возрастает: max C(x) = CA (t), min CA(x) = CA (1).

,

5. Исследуем норму прибыли банка:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Как вычисляются процентные деньги в схеме простых процентов?

2.Как определяются операции наращения и дисконтирования в схеме простых процентов с процентной ставкой?

3.Как определяется учетная ставка и в чем заключается ее экономический

смысл?

4.Какие соотношения связывают учетную и процентную ставки?

2.СЛОЖНЫЕ ПРОЦЕНТЫ

2.1.Понятие сложных процентов

2.2.Номинальные процентные ставки

2.3.Коэффициенты накопления

2.1.Понятие сложных процентов

Простые проценты имеют ограниченное практическое применение. Пусть по некоторому типу сберегательного счета выплачиваются простые проценты по ставке i в год. Предположим, что эти проценты гарантируются в течении двух лет, а счет можно закрыть в любое время. Пусть вкладчик открывает в некоторый момент счет с начальным вкладом Р, через год закрывает его и по формуле простых процентов получает сумму А = P(1 + i). Затем открывает новый счет с суммой А, которая через год дает сумму А1 = Р (1

10