
5540
.pdf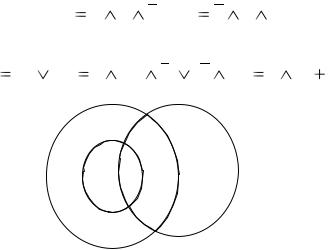
Можно составить обратную задачу, т.е. по известной диаграмме (рисунок 2.9) находить отвечающее ей компактное аналитическое выражение. Для этого заштрихованные области представим в виде конституент:
С1 a b c, C2 a b c.
Искомое выражение получается при объединении этих конституент: x C1 C2 b ((a c) (a c)) b (a c).
а
C2
c C1
b
Рисунок 2.9 – Обратная задача
Позиция конструктивистов состоит в том, что в математической логике каждое тождество должно получить своё убедительное обоснование, т.е. не должно быть никаких аксиом – утверждений без доказательств.
Задача 2.1. Представьте в явном виде булеву функцию, заданную таблицей:
a |
b |
c |
f(a, b, c) |
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
0 |
1 |
1 |
1 |
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
Задача 2.2. Используя СДНФ, найдите булеву функцию, принимающую значение 1 на следующих наборах переменных, и только на них:
f(1, 0, 1) = f(0, 1, 0) = f(1, 1, 1) = 1.
41

Задача 2.3. Ниже приведены логические функции. Максимально упростите функции, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощённое выражение с исходным.
а) (a c) (a b) (b c) (a b) (c b);
б) (a c) (a b) (b c) (a b) (b c).
Задача 2.4. Аналитическим способом докажите справедливость нижеприведённых тождеств. Затем с помощью диаграмм Эйлера – Вена и с помощью таблицы истинности подтвердите справедливость этого
доказательства. |
|
|
|
1) a (b c) |
a | (b | c); |
||
2) (a b c) |
(a b c) (a b) (b c) (c a); |
||
3) (a b) (a | b) |
a b; |
||
4) a b (a b) |
(b a); |
||
5) a ((b |
a) |
b) |
0; |
6) (a | b) |
(b c) |
b c. |
|
Задача 2.5. Ниже приведены диаграммы Эйлера – Вена. Представьте заштрихованные и отдельно не заштрихованные области максимально компактными аналитическими выражениями, в которых бы использовалось минимальное количество логических операций и букв. С этой целью сначала выразите все заштрихованные области через конституенты – конъюнкты, а незаштрихованные – через конституенты – дизъюнкты, и только после этого приступайте к упрощению совершенных форм (результаты проверьте на таблицах истинности).
1. |
|
|
2. |
|
|
А |
В |
|
|
|
|
|
|
|
|
|
С |
В А |
С |
|
|
|
|
42
Глава 3. ЛОГИКА ВЫСКАЗЫВАНИЙ
3.1 Классическая логика
Умение правильно рассуждать необходимо в любой области человеческой деятельности: науке и технике, юстиции и дипломатии, планировании народного хозяйства и военном деле. Но, хотя это умение исходит к древнейшим временам, логика, т. е. наука о том, какие формы рассуждений правильны, возникла лишь немногим более двух тысяч лет тому назад. Она была развита в IV веке до н.э. в работах великого древнегреческого философа Аристотеля, его учеников и последователей. Аристотель исследовал различные формы суждений и их комбинации, ввёл понятие силлогизма, т.е. рассуждения, в котором из заданных двух суждений выводится третье. Примером силлогизма может служить такое рассуждение: «Все млекопитающие имеют скелет. Все киты – млекопитающие. Следовательно, все киты имеют скелет». Ту же форму имеет силлогизм «Все квадраты ромбы, все ромбы – параллелограммы. Следовательно, все квадраты – параллелограммы». В общем виде этот силлогизм имеет форму: «Все a есть b; все b есть с. Следовательно, все а есть с». А вот пример силлогизма неправильной формы: «Все квадраты – ромбы. Некоторые ромбы имеют острый угол. Некоторые квадраты имеют острый угол». Хотя оба утверждения, из которых был сделан вывод, истинны, сам вывод о существовании квадратов с острым углом ложен. Значит, силлогизм, имеющий форму: «Все а есть b, некоторые b есть с. Значит, некоторые а есть с», может привести и к ложным выводам. Аристотель выделил четыре типа суждений:
 общеутвердительные – «Все а есть b»;
общеутвердительные – «Все а есть b»;
 частноутвердительные – «Некоторые а есть b»;
частноутвердительные – «Некоторые а есть b»;
 общеотрицательные – «Все а не есть b»;
общеотрицательные – «Все а не есть b»;
 часноотрицательные – «Некоторые а не есть b».
часноотрицательные – «Некоторые а не есть b».
Для проверки правильности силлогизмов можно использовать метод, основанный на теории множеств. Суждения, из которых строятся силлогизмы, являются на самом деле высказываниями о множествах.
43
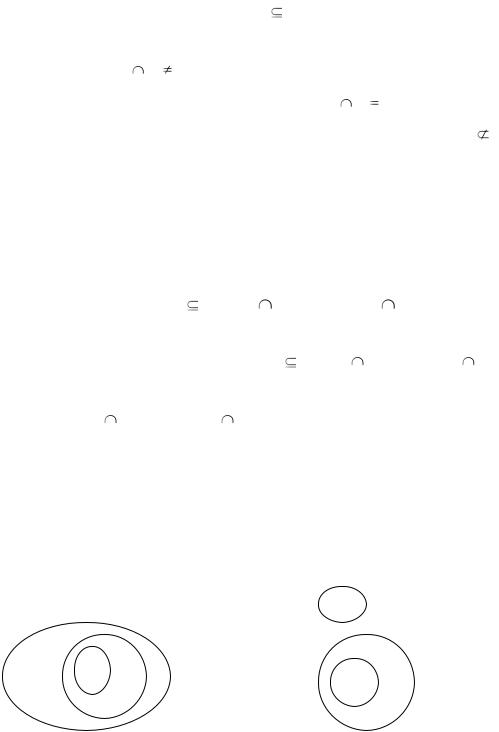
Например, утверждая, что «Все а есть b», мы говорим, что множество А всех а – подмножество множества В всех b, А В. Утверждая, что «Некоторые а есть b», мы говорим, что пересечение множеств А и В непусто (предполагаем,
что А и В непусты), А |
В |
Ø. Утверждение «Ни одно а не является b» |
||
говорит, что А и В |
не |
пересекаются, т.е. А |
В |
Ø, а утверждение |
«Некоторые а не являются b» – что А не есть подмножество В, т.е. А В . |
||||
Поскольку множества можно изображать |
в |
виде геометрических |
||
фигур, логические рассуждения тоже изображаются геометрически. Например, рисунок 3.1 поясняет, что «Если все а есть b, а все b есть с, то все а есть с» (если А  В и В
В и В  С, то А
С, то А  С). Рисунок 3.2 служит для пояснения силлогизма «Если все а есть b и ни одно b не является с, то ни одно а не является с» (если А В и В С = Ø, то А С = Ø). А рисунок 3.3 а) поясняет, почему не годится силлогизм «Все а есть b, некоторые b есть с. Значит, некоторые а есть с», хотя А В и В С
С). Рисунок 3.2 служит для пояснения силлогизма «Если все а есть b и ни одно b не является с, то ни одно а не является с» (если А В и В С = Ø, то А С = Ø). А рисунок 3.3 а) поясняет, почему не годится силлогизм «Все а есть b, некоторые b есть с. Значит, некоторые а есть с», хотя А В и В С  Ø, но А С может быть и пустым множеством. Впрочем, на рисунке 3.3 б) показан случай, когда А
Ø, но А С может быть и пустым множеством. Впрочем, на рисунке 3.3 б) показан случай, когда А  В и В С
В и В С  Ø, и А С
Ø, и А С  Ø, т.е. некоторые а есть с. Это показывает, что неправильно построенное рассуждение не обязательно приводит к ложному выводу: случайно может оказаться так, что вывод будет истинным. Но логика считает допустимым только такие формы рассуждений, которые гарантируют истинный результат во всех случаях, когда исходные утверждения истинны.
Ø, т.е. некоторые а есть с. Это показывает, что неправильно построенное рассуждение не обязательно приводит к ложному выводу: случайно может оказаться так, что вывод будет истинным. Но логика считает допустимым только такие формы рассуждений, которые гарантируют истинный результат во всех случаях, когда исходные утверждения истинны.
|
|
|
С |
С |
|
В |
В |
|
А |
||
|
|
А |
|
|
|
|
Рисунок 3.1 – Логическое |
Рисунок 3.2 – Логическое |
рассуждение |
рассуждение |
44
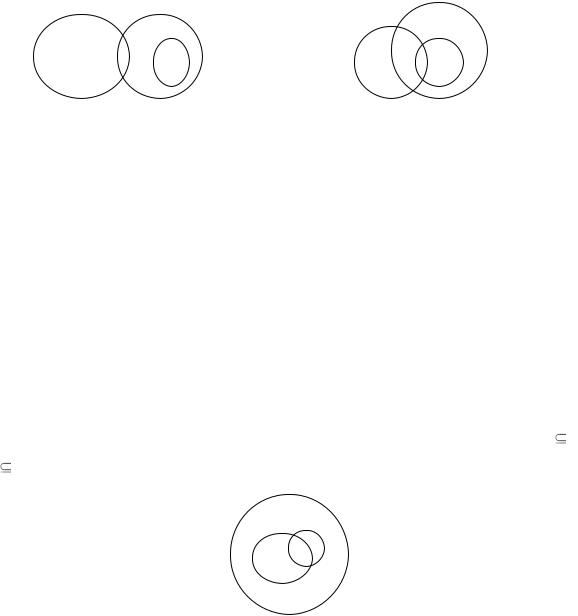
С |
В |
|
В |
С |
|
||
|
А |
А |
|
|
|
а) |
б) |
|
Рисунок 3.3 – Логические рассуждения |
Пример 3.1. Для следующего рассуждения постройте его буквенную форму и проверьте с помощью диаграмм Эйлера – Вена, правильна ли эта форма: «Если всех хищников можно приручить и всех львов можно приручить, то все львы хищники».
Решение. Обозначим через а – хищника, через b – животное, которое можно приручить, через с – льва. Буквенная форма рассуждения имеет вид: «Если все а являются b и все с являются b, то все с являются а».
Обозначим через А, В и С множества, элементами которых, соответственно, являются а, b и с. Тогда условие примера имеет вид: А В,
СВ. На диаграмме Эйлера – Венна (рисунок 3.4) это выглядит так:
В
С
А
Рисунок 3.4 – Диаграмма Эйлера – Венна
Из диаграммы видно, что могут быть такие элементы с из множества С, которые не принадлежат множеству А. Значит рассуждение неправильное.
Задача 3.1. Нарисуйте диаграммы Эйлера – Венна, иллюстрирующие суждения:
а) все а являются b;
б) некоторые а являются b; в) ни одно а не является b;
г) некоторые а не являются b.
45
Задача 3.2. Проанализируйте рассуждения, приведённые ниже. Какие из этих рассуждений имеют правильную форму? В каких из них истинны посылки? В каких из них истинны заключения? Можно ли из ложных посылок путём правильных рассуждений получить истинное заключение?
1.Все писатели – деятели искусства. Некоторые деятели искусства – талантливые люди. Значит, некоторые писатели талантливы.
2.Все люди смертны. Все люди – живые существа. Значит, все живые существа смертны.
3.Все кошки являются рыбами, у всех рыб – четыре ноги. Значит, у кошки четыре ноги.
4.Некоторые позвоночные являются млекопитающими, и некоторые позвоночные являются лягушками. 3начит, некоторые лягушки – позвоночные.
Однако использование диаграмм Эйлера – Венна затруднительно в сложных случаях. Чтобы облегчить проверку и преобразование сложных цепочек рассуждений, было создано особое буквенное исчисление. Оно получило название алгебры логики или математической логики. Основы математической логики были заложены в XVII веке великим немецким математиком Г. Лейбницем (1646 – 1716 гг.). В середине ХIХ века ирландский математик и логик Джордж Буль (1815 – 1864 гг.) своими трудами положил начало формированию математической (символической) логики как научной дисциплины. Современная символическая логика для анализа дедуктивных рассуждений строит особые логические системы; одна из них называется логикой высказываний, другая – логикой предикатов. Рассмотрим принципы построения логики высказываний. Логика высказываний – это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и отвлекаясь от внутренней структуры суждений.
3.2 Высказывания
В логике высказыванием называют любое утверждение, относительно которого имеет смысл говорить, что оно либо истинно, либо ложно.
46

Высказывания могут быть выражены с помощью слов, а также математических, химических и прочих знаков. Например:
–«Все люди смертны» (истинное высказывание);
–«2 + 6 > 8» (ложное высказывание).
Не каждый набор слов и даже не каждое утверждение являются высказыванием. Например, восклицательные и вопросительные предложения высказываниями не являются. Не являются высказываниями пословицы и поговорки, а также определения. Определения не могут быть истинными или ложными, они лишь фиксируют принятое использование терминов. Не являются высказываниями и предложения «Он сероглаз» или «х2 – 4х + 3 = 0» – в них не указано, о каком человеке идёт речь или для какого числа х верно равенство х2 – 4х + 3 = 0.
Утверждения должны быть чёткими и однозначно понимаемыми. Эта цель достигается использованием высказываний и логических связок, позволяющих из существующих высказываний формировать другие высказывания. Существует пять логических связок: частица не и союзы
…и…; …или…; если…, то…; … тогда и только тогда, когда… .
Высказывания, сформированные без использования логических связок, называются элементарными (простыми) высказываниями.
Высказывания, сформированные с использованием логических связок, называются сложными (составными) высказываниями.
Высказывания обозначаются прописными буквами латинского алфавита: A, B, C, D, … или строчными буквами латинского алфавита: a, b, c, d, … .
Каждая логическая связка имеет для обозначения свой собственный символ и производит логическую операцию над высказываниями: отрицание, конъюнкцию, дизъюнкцию, импликацию, эквиваленцию. Естественно, они определяются на основе введённых ранее соответствующих булевых функций с учётом чисто логической специфики.
1. A (читается не A) обозначает высказывание, противоположное высказыванию A и называется отрицанием высказывания A. Данное высказывание истинно, когда A ложно и ложно, когда A истинно.
47

Вопрос: как выглядит отрицание высказывания «число 6 делится на 2»?
2. A B (читается A и B) обозначает высказывание, истинное только тогда, когда A и B оба истинны и называется конъюнкцией высказываний A и B.
Например, пусть А – высказывание «Число 5 больше 2», и В – высказывание «Число 5 меньше 10». Каждое из них истинно.
Высказывание А |
В в данном примере – это предложение «Число 5 |
|||
больше 2 и меньше 10». Такое высказывание истинно. |
||||
3. A |
B |
(читается A или B) обозначает высказывание, истинное |
||
тогда, когда истинно хотя бы одно из высказываний A и B (или оба) и |
||||
называется дизъюнкцией высказываний A и B. |
|
|||
Например, пусть А – высказывание «Число 28 делится на 7», и В – |
||||
высказывание «Число 28 делится на 2». Тогда А |
В есть высказывание |
|||
«Число 28 делится на 7 или на 2». Это высказывание истинно. |
||||
4. A |
B (читается если A, то B) обозначает высказывание, истинное |
|||
во всех случаях, кроме того, когда A истинно, а B ложно, и называется |
||||
импликацией высказываний A и B. |
|
|||
5. A |
B |
(читается A тогда и только тогда, когда B) обозначает |
||
высказывание, |
истинное только тогда, когда A и B оба истинны или оба |
|||
ложны, и называется эквиваленцией высказываний A и B.
Например, пусть А – высказывание «Число 28 делится на 2», и В – высказывание «Число 28 чётное». Тогда А ↔ В есть высказывание «Число 28 делится на 2 тогда и только тогда, когда, оно чётное». Это высказывание истинное.
В обыденной речи союз «или» имеет два различных значения – разделительное и неразделительное. Например, если сказать: «Завтра в 12 часов дня я буду в клубе или на катке», то не может быть, чтобы оба обещания оказались выполнены: человек не может быть одновременно в двух местах. Здесь союз «или» разделительный. Но если сказать: «Я буду в клубе завтра в 12 часов дня или в 6 часов вечера», то отнюдь не исключено, что сбудется и то, и другое – человек может посетить клуб дважды в один и тот же день. Здесь тоже союз понимается в
48

неразделительном смысле. Чтобы устранить эту неопределённость, условились в логике использовать лишь неразделительное «или».
Логический союз «и» не обязательно должен представляться через грамматический союз «и». Союзы «а» и «но» по смыслу часто совпадают с союзом «и», поэтому они используются в сложных конъюнктивных предложениях.
Однако языковая ситуация может стать такой, что союз «и» перестаёт играть роль конъюнкции:
«Ему стало страшно и он убил человека», «Он убил человека и ему стало страшно».
Здесь некоммутативность двух простых предложений очевидна, поскольку мы имеем дело со скрытой импликацией, когда одно простое предложение обусловливает другое.
Наглядное представление о сочетаниях истинности или ложности первоначальных высказываний и высказываний, полученных из них в результате проведения логических операций, позволяют получить таблицы истинности. В них в строках даются все возможные сочетания значений истинности первоначальных высказываний, и для каждого из этих сочетаний даётся значение истинности для высказывания, полученного в результате логических операций над первоначальными высказываниями. Истинность высказывания обозначается цифрой 1 (или буквой И), ложность – цифрой 0 (или буквой Л).
В случае если высказывание образовано логическими операциями из
n первоначальных высказываний, таблица истинности будет иметь 2 n строк.
Приведём сводную таблицу истинности для рассмотрения логических операций (таблица 3.1). Поскольку отрицание содержит одно первоначальное высказывание А, то его таблица истинности содержит
21 2 строки (в сводной таблице в лишних строках прочерки). Остальные операции содержат два первоначальных высказывания A и B,
следовательно, их таблицы истинности содержат 22 4 строки.
49

Таблица 3.1 – Сводная таблица истинности
A |
B |
|
A |
A B |
A B |
A B |
A B |
|
|
|
|
|
|
|
|
0 |
0 |
|
– |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
– |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
Указание: несмотря на то что всем логическим связкам соответствуют слова русского языка, логический смысл истинности логических операций отличается от смыслового значения этих слов в русском языке. Нахождение значения истинности каждой логической операции возможно только согласно её определению и соответствующей таблице истинности по значениям истинности первоначальных высказываний, входящих в эту логическую операцию.
Например, дано высказывание: если 9 чётное число, то 2 делитель 9. A B ; A = 0 (ложно) B = 0 (ложно). По определению импликации
A B = 1 (истинно).
Пример показывает, как ошибочные (ложные) предпосылки при правильно проведённых логических рассуждениях приводят к ошибочным (ложным) выводам.
В общем случае элементарные высказывания, входящие в логическую операцию, могут не иметь между собой смысловой связи с точки зрения грамматики. Полученное сложное высказывание также не будет иметь грамматического смысла. Нас интересует исключительно логический смысл полученного сложного высказывания.
С точки зрения математической логики каждое ложное высказывание отождествляется не с ошибочным отождествлением действительности, а с пустым множеством. Соответственно, каждое истинное высказывание отождествляется с непустым множеством элементов, чья физическая природа не принимается во внимание.
Например, дано высказывание: Если погода жаркая, то уголь белый.
50
