
5514
.pdfМинистерство образования и науки Российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
Е. А. Мясников
М. Ф. Тиунчик
ЧИСЛЕННЫЕ МЕТОДЫ
Учебное пособие
Часть 1
Хабаровск 2013
1
УДК 519. 95
ББК В 1
М 99
Мясников Е. А. Численные методы. Часть 1 : учеб. пособие / Е. А. Мясников, М. Ф. Тиунчик. – Хабаровск : РИЦ ХГАЭП, 2013. − 80 с.
Учебное пособие предназначено для бакалаврантов и магистрантов экономических вузов всех направлений и профилей подготовки, изучающих отдельными дисциплинами линейную алгебру и математический анализ. В нём рассматриваются только численные методы решения математических и прикладных задач указанных дисциплин. Настоящая первая часть посвящена методам линейной алгебры. Кроме того, приведены основные требования к численным методам, их роли и назначению; кратко описаны действия с приближёнными величинами.
Рецензенты:
Р. В. Намм, доктор физ.-мат. наук, профессор, гл. научный сотрудник ВЦ ДВО РАН
С. В. Соловьёв, доктор физ.-мат. наук, профессор кафедры прикладной математики ТОГУ
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
©Мясников Е. А., Тиунчик М. Ф., 2013
©Хабаровская государственная академия экономики и права, 2013
2
§ 1. Основные сведения о численных методах 1.1 . Приближённые методы и их назначение
Методы решения математических задач можно условно разделить на точные (аналитические) и приближенные (численные). При решении точными методами ответом обычно служит формула для вычисления неиз-
вестных элементов(чисел, функций). |
|
|
|
|||||
Так, |
корни |
уравнения |
|
4x2 |
|
3x 2 0 находят |
подстановкой |
|
a 4, b |
3, c 2 в известную формулу |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x1,2= |
b |
|
b2 4ac |
|
, |
|
|
|
|
2a |
|
|
|||
|
|
|
|
|
|
|
||
правая часть которой представляет собой элементарную функцию пара-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метров a, b, c . При этом получают два решения |
x |
|
3 41 |
и x |
|
3 41 |
. |
|||||||
|
|
|
|
1 |
|
|
8 |
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для дифференциального уравнения y |
a2 y |
|
ekx при a 0 также суще- |
|||||||||||
ствует точное решение, а именно функция |
|
|
|
|
|
|
|
|
|
|
|
|||
y x C cos ax |
C |
|
sin ax |
|
|
|
ekx . |
|
|
|
|
|
||
|
k 2 |
|
a2 |
|
|
|
|
|
||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Решение называют точным (аналитическим), если формула, его выражающая, есть элементарная функция. Однако понятие точности здесь достаточно условно. Даже в теоретической задаче элементарные функции в произвольной точке, как правило, можно найти лишь приближённо. Так, 
 41, ln 10 , arcsin 0,8 − бесконечные непериодические дроби. Любая попытка записать их в виде чисел приводит к округлению и, следовательно, к потере точности.
41, ln 10 , arcsin 0,8 − бесконечные непериодические дроби. Любая попытка записать их в виде чисел приводит к округлению и, следовательно, к потере точности.
Если же математическая задача служит моделью реального процесса, входные данные модели всегда измеряются неточно и подстановка их в точную формулу погрешность не исправит.
Кроме того, не каждую математическую задачу можно решить точно. Например, нет общей формулы для корней уравнения ln x kx b при b 0 , поскольку эти корни нельзя выразить через элементарные функции от параметров k и b. Корни можно найти графически или постепенным уточнением, причём параметры k, b должны быть заранее известны.
3
1 |
|
|
|
|
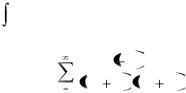
Другой пример: интеграл sin x2 dx |
можно вычислить с какой угодно |
|||
0 |
|
|
|
|
|
|
|
1 n |
|
точностью, представив в виде ряда |
|
|
|
, но нельзя найти по |
n 0 |
|
2n 1 ! 4n 3 |
||
формуле Ньютона-Лейбница, так как первообразная для функции sin( x2 ) не выражается в виде элементарной функции. Эта задача также допускает лишь приближённое решение.
При численном (приближённом) решении выполняется конечная последовательность арифметических операций с числами, а непрерывные переменные заменяются дискретными, принимающими значения с некоторым шагом. Так, приближённое вычисление определённого интеграла сводится к выполнению операций над значениями функции в различных точках отрезка.
Ответом при численном решении служит или число, найденное путём приближений с необходимой точностью, или таблица чисел − значений искомой функции в разных точках, и лишь иногда – формула для вычисления функции. Причём в любом случае и значения, и формулы приближённые.
Широкое применение численных методов объясняется не только отсутствием или сложностью точных формул для решения некоторых математических задач, но еще и особенностями постановки и решения прикладных задач. Работу с любой задачей, имеющей отношение к действительности, можно разделить на несколько этапов.
1-й этап − построение предметной модели. Задача ставится в терминах проблемной области (экономики, космонавтики, управления и т.п.). Выясняются объекты исследования, связи между ними, факторы, влияющие на эти связи.
2-й этап − построение математической модели. Связи описываются математически − формулами, уравнениями, системами.
3-й этап − составление алгоритма решения. Математическая модель сводится к строгой последовательности задач, и решение каждой задачи служит входными данными для другой.
4
4-й этап − реализация алгоритма, обычно в виде компьютерной программы; тестирование и отладка.
5-й этап − решение задачи при помощи полученной программы и анализ результатов.
На каждом этапе возможен, а фактически всегда происходит, возврат к предыдущим шагам, необходимость которого очевидна из описания этапов.
Уже на 1-м этапе в решении задачи появляются погрешности, связанные с отбрасыванием многочисленных факторов. Не все факторы, влияющие на решение, могут быть известны, а учёт известных может весьма усложнить задачу. Иногда учёт фактора почти не отражается на результатах, иногда многое меняет, причём что именно произойдёт в конкретном случае, предсказать трудно.
Математическая модель (на 2-м этапе) ещё более отдаляет задачу от реальности, так как формулы упрощают зависимость.
Допускает ли задача математическое решение по точным формулам выясняется именно на 3-м этапе. Однако погрешности, возникшие на 1-м и 2-м этапах, делают бессмысленным такое решение, поскольку точность приближённого метода обычно намного выше, чем точность модели и точность входных данных. В прикладной задаче входные данные – это или результаты измерений, или ограниченная выборка сведений. Кроме того, точное решение часто не оправдывает себя как очень длинное и громоздкое (например, вычисление интегралов), а быстрота решения важна в режиме реального времени (управление полетом, обслуживание и т.д.).
На 4-м этапе возникают и накапливаются ошибки округления, связанные с конечностью разрядной сетки компьютера. Для многих практических задач эти ошибки несущественны, но там, где происходит до нескольких трлн операций (в метеорологии, астрономии, космонавтике и т.п.) и при этом нужна высокая точность, возможность работать с большим числом точных цифр очень важна.
Наконец, если результат решения задачи − значение, используемое в практических целях (например, объём средств, распределяемых между объектами), то на 5-м этапе также возникнут погрешности, поскольку большинство реальных величин, даже непрерывных теоретически, в жизни
5

меняется дискретно (зарплата начисляется с каким-то шагом, продукты пакуются в ящики и т.п.)
Таким образом, решение любой прикладной задачи связано с многочисленными упрощениями, округлениями, погрешностями, на фоне которых ошибки приближённого решения математической части не так существенны.
С точки зрения численных методов, при решении математической задачи погрешности бывают трёх типов:
1)неточности входных данных;
2)погрешности приближённого метода;
3)ошибки округления.
Уточнение входных данных − задача специалистов проблемной области, но теория ЧМ (численных методов) указывает, как ошибки в данных отражаются на результатах. Подробно изучены погрешности 2-го типа, известны формулы их оценки при решении математических задач. Правильное округление результатов − также важный практический вопрос, знание которого ускоряет решение.
1.2. Общие требования к численным методам решения задач
Основное требование, предъявляемое к вычислительному методу или алгоритму − требование точности, что никак не противоречит идее ЧМ. Требование означает, что метод должен давать решение задачи с любой заранее указанной точностью за конечное число действий. Так, для специалиста по ЧМ нет смысла в формуле
|
1 |
1 |
|
1 |
|
( |
1)n 1 |
||
ln2 =1 |
|
|
|
|
|
... |
|
|
... , |
|
|
|
|
|
|
|
|||
|
2 |
3 |
4 |
|
|
n |
|||
поскольку для её применения надо выполнить бесконечное число действий. Однако запись
ln 2 1 |
1 |
|
1 |
|
1 |
... |
1 n 1 |
с погрешностью |
1 |
|
2 |
3 |
4 |
n |
n 1 |
||||||
|
|
|
||||||||
вполне законна, поскольку указывает, что для достижения точности
необходимо найти сумму n слагаемых, где n 1 |
1 |
|
|
|
Во избежание недоразумений заметим, что в ЧМ под возрастанием (повышением) точности понимают уменьшение погрешности вычислений,
6

а бесконечная точность равносильна нулевой погрешности (и то, и другое теоретически недостижимо). Повысить точность в 10 раз − значит в 10 раз уменьшить погрешность, то есть ещё одну цифру в записи ответа сделать заслуживающей внимания ("верной"). Подробнее этот момент изложен в § 2.
Понятие точности означает принципиальную возможность получить решение с любой точностью, но в силу ограниченных, хотя и постоянно растущих возможностей компьютера, завышенные требования могут привести к недопустимо большому времени счёта. Отсюда возникает требова-
ние реализуемости алгоритма.
Так, решение системы уравнений по формулам Крамера − хороший тренировочный пример при обучении программиста, но соответствующий алгоритм не подходит для реальной экономической задачи с пятизначным числом уравнений и тем более для задачи, решаемой в режиме реального времени.
С реализуемостью связано понятие экономичности, когда из нескольких алгоритмов предпочтительнее тот, что позволяет достичь необходимой точности за меньшее число действий. Так, метод Гаусса универсален и позволяет решить систему 1000-го порядка примерно за 8 млрд операций, но для распространённых в экономике систем с разреженными матрицами (когда большинство коэффициентов равны 0 или близки к 0) лучше подойдёт метод прогонки, решающий ту же систему с той же точностью примерно за 20 тыс операций.
Безаварийность алгоритма связано с конечностью чисел, обрабатываемых компьютером, и относится скорее к области программирования. При умножении больших чисел может произойти переполнение, и результат с точки зрения компьютера станет бесконечным. Наоборот, произведение слишком малых чисел часто обращается в 0 и происходит полная потеря результатов, заметить которую очень сложно.
Пусть, например, компьютер может работать с числами от 10 50 до 1050 , а надо перемножить 10 30,10 40,1035 и 1060 . Попытка умножения в указанном порядке приведёт к получению 0, поскольку 10 3010 40 10 70 . Умножение в обратном порядке ведёт к переполнению: 10351060 1095 . Допусти-
мый порядок: 10 30103510 401060 1025 или 10 30106010 401035 1025 .
7

Алгоритм устойчив, если погрешности округления не накапливаются в процессе вычислений, неустойчив при их неограниченном возрастании, и условно устойчив, если погрешность нарастает по степенному закону, т.е. получается устойчивость при некоторых ограничениях на объём вычислений. Например, вычисление последовательности yi 1 ayi устойчиво при a 1 и неустойчиво при a 1. Приведение определителей к треугольному виду условно устойчиво, и для повышения точности проводят вычисления с несколькими запасными цифрами. Условно устойчивы некоторые методы решения систем уравнений.
Требования предъявляются не только к методам решения, но и к самим задачам. Основное из них − требование корректности. Задача поставлена корректно, если:
1)она разрешима при любых допустимых входных данных;
2)решение единственно;
3)малое изменение входных данных ведёт к малому изменению ре-
шения.
Последнее условие означает непрерывность решения по входным данным, т.е. устойчивость задачи. Например, приближённое интегрирование корректно для любой ограниченной функции. Система уравнений некорректна, если её определитель близок к 0, что следует хотя бы из формул Крамера. Некорректно также численное дифференцирование, особенно при большой погрешности аргументов.
Почти все численные методы решения задач можно условно разде-
лить на сеточные и итерационные.
Первые методы или дают решение в виде таблично заданной функции, как, например, при численном решении задачи Коши на отрезке; или используют такую таблицу для получения результата, как при интегрировании по квадратурным формулам.
Вторая группа методов сводится к подбору некоторого начального решения с последующим уточнением. Так решают нелинейные уравнения или системы, находят корни из чисел.
Несколько в стороне стоят задачи приближения функции и родственные им, когда решением служат коэффициенты полинома, получае-
8
мые по точным формулам. Однако при поиске полиномов возникают вспомогательные задачи, решаемые указанными методами − системы уравнений, интегралы и т.д.
Отметим важнейшие типы задач, решаемых в курсе ЧМ:
1)нелинейные функциональные уравнения с одним неизвестным;
2)системы линейных алгебраических уравнений;
3)системы нелинейных уравнений (необязательно алгебраических);
4)приближение функций;
5)интегрирование и дифференцирование функций;
6)интегрирование дифференциальных уравнений и систем Повышение точности, уменьшение числа действий, сокращение за-
нимаемой памяти и связанная с этими противоречащими друг другу задачами оптимизация алгоритмов многие годы были важнейшими вопросами в ЧМ, особенно во время первых ЭВМ. Сейчас появилось множество пакетов прикладных программ (ППП), позволяющих быстро решать многие задачи, не думая о возникающих вычислительных сложностях и даже о самих алгоритмах (в приложении указаны некоторые возможности распространённого пакета EXCEL по решению типовых задач и вопросы, остающиеся открытыми).
Решение практических задач стало доступно не только профессиона- лу-математику, но и специалисту в проблемной области. Тем не менее, знание основных методов решения задач, представление о достигаемой при этом точности и способах её оценки позволяют создавать собственные программы с высокими возможностями и оценивать результаты их работы.
Утверждение же, что ЧМ наряду с методами оптимизации устарели, бессмысленно, поскольку именно на этих дисциплинах основаны все прикладные пакеты.
В пособии принята следующая схема изложения:
1) задача, её смысл и актуальность указаны с точки зрения математи-
ки;
2)приводится общая схема действий и формулы решения;
3)приведён пример с комментариями;
4)предложен удобный способ записи решения.
9

При изучении примеров следует помнить, что почти все результаты вычислений приближённые, поэтому равенства выполнены с точностью до приведённых десятичных знаков.
§ 2. Действия с приближёнными величинами 2.1. Погрешности приближений
Пусть х – точное значение некоторой величины, а а – её приближённое значение. Запись х ≈ а означает, что число х приближённо равно числу
а.
Если а < х, то а называют приближённым значением числа х с недостатком, если a > x, то a называют приближенным значением числа x с избытком.
Разность
а = х – а
между точным и приближённым значениями величины называют погрешностью приближения. Число а может быть как положительным, так и отрицательным. Модуль разности точного и приближённого значений ве-
личины называется абсолютной погрешностью приближения и обозна-
чается Δ, т.е.
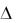
 х а .
х а .
Абсолютная погрешность и есть характеристика приближения к неизвестной величине х. Если точное значение величины неизвестно, то эта характеристика представляет лишь теоретический интерес. Поэтому целесообразно ввести оценку абсолютной погрешности.
Предельной абсолютной погрешностью приближения называется
такое число а > 0, что |
|
|
|
|
|
х а |
|
а . |
(2.1) |
|
|
|||
Последнее неравенство равносильно неравенствам |
||||
а – а ≤ х ≤ а + |
а. |
|||
Это значит, что а – а будет приближённым значением х с недостатком, а а + а – приближённым значением х с избытком. При этом применяют запись
х = а ± а
и говорят, что а есть приближённое значение х с точностью до а.
10
