
5358
.pdf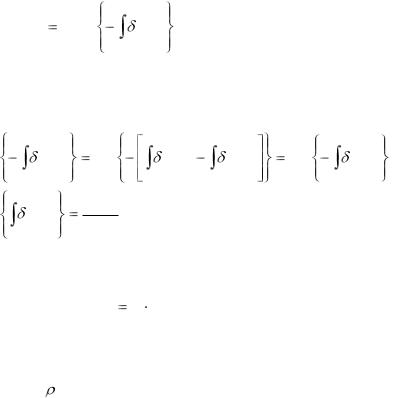
5.3.Оценка текущей стоимости потока наличности
Впредыдущем разделе была выведена формула текущей стоимости в начальный момент времени t0. Поставим более общую задачу: найти текущую стоимость на любой момент t и найти простую формулу,
позволяющую произвести перерасчет текущей стоимости с момента t1 на момент t 2 .
Рассмотрим моменты времени t1 и t2, причём не обязательно t2 больше t1.
Определение. Стоимостью А на момент времени t1 суммы С, выпла-
чиваемой в момент времени t2, называется: а) накопление С на срок от t2 до t1 при t1 > t2;
б)дисконтированная стоимость на момент t1 суммы С, выплачиваемой в момент времени t2, если t2 > t1.
В обоих случаях эта величина А находится по формуле
|
t2 |
|
А С exp |
(t)dt . |
(5.7) |
|
t1 |
|
Воспользуемся теперь свойствами интеграла и показательной функции:
t2
exp (t)dt
t1
t1
exp (t)dt
0
t2 |
|
t1 |
|
t2 |
exp |
(t)dt |
(t)dt |
exp |
(t)dt ; |
0 |
|
0 |
|
0 |
V (t2 ) .
V (t1 )
Тогда формула (5.7) примет вид: |
|
|
|
|
A C |
V (t |
2 ) |
. |
(5.8) |
V (t1 ) |
|
|||
|
|
|
||
Найдём текущую стоимость на момент t(1) заданного потока наличности
(заданы С и норма (t)).
Для этого достаточно воспользоваться формулой (5.6) и формулой (5.8),
где t1=t(1):
42
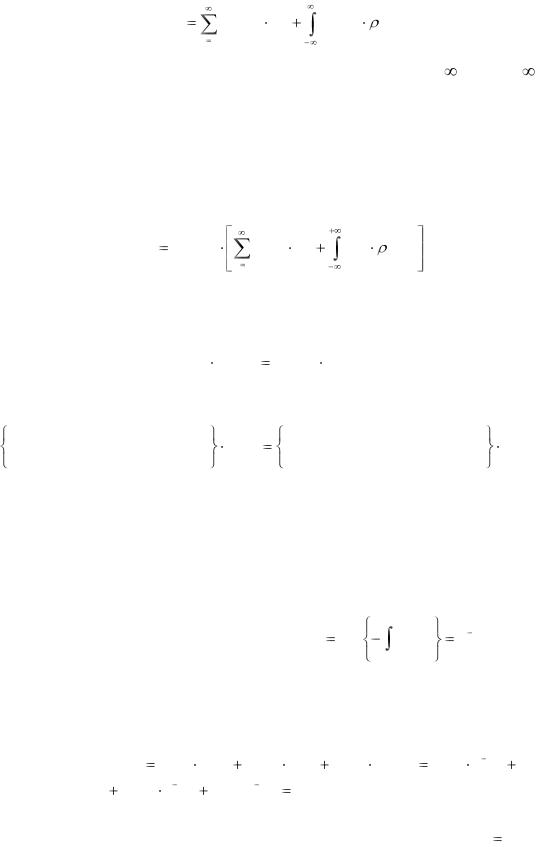
|
A(t (1) ) |
|
V (t j ) |
C |
|
V (t) |
(t)dt. |
|
|
(5.9) |
|
|
|
j |
|
|
|
|
|||
|
j 1 V (t (1) ) |
V (t (1) ) |
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
В формуле |
(5.9) интегрирование |
ведётся от – |
до + , |
так |
как |
|||||
учитываются все платежи при t < t(1) и при t > t(1). |
|
|
|
|||||||
Рассмотрим |
теперь |
другой фиксированный момент |
времени |
t(2) |
и |
|||||
найдём текущую стоимость данного потока на момент t(2). По аналогии с формулой (5.9) будем иметь
A(t (2) ) |
1 |
V (t j ) C j V (t) (t)dt . |
|
(5.10) |
||
|
|
|
|
|||
V (t (2) ) |
|
|
||||
|
j 1 |
|
|
|
||
Сравнивая формулы (5.9) и (5.10), получим |
|
|
||||
|
A(t (1) ) V (t (1) ) |
A(t (2) ) V (t (2) ). |
|
(5.11) |
||
Равенство (5.11) символически можно изобразить следующим образом: |
||||||
стоимость потока наличности |
V (t1 ) |
стоимость потока наличности |
V (t2 ). |
(5.12) |
||
на момент t1 |
|
|
на момент t 2 |
|
||
|
|
|
|
|
||
Пример 5.2. Бизнесмен должен уплатить 1 000 у.д.е. 1 января 1986 г. 2
500 у.д.е. 1 января 1987 г. и 3 000 у.д.е. 1 июля 1987 г. Полагая силу процента постоянной и равной 0,06 в год, найти стоимость этих платежей на а) 1 января 1984 г., б) 1 марта 1985 г.
t
Решение. Найдём вначале V(t): V (t) exp 0,06dt e 0,06t .
0
Воспользуемся формулой (5.9), полагая t(1)= 0, т.е. за нулевую точку отсчёта взяв 1 января 1984 г.:
A(O) |
1 000 V (2) 2 500 V (3) 3 000 V (3,5) 1 000 e 0,12 |
2 500 |
e 0,18 3 000e 0,21 5 406,86 у.д.е. |
б) воспользуемся формулой (5.11), полагая t(1) = 0, t (2) |
14 |
, А(0) = 5 |
|
||
12, |
|
|
406,86:
43

A(t (2) ) 5 406,86 |
1 |
|
5406,86 |
|
1 |
|
|
|
5 798,89 у.д.е. |
|
|
|
|
|
|
|
|
|
|||
14 |
|
|
0,06 |
14 |
||||||
|
|
|
|
|
||||||
|
|
|
е |
|
|
|
|
|||
|
V ( ) |
|
|
12 |
|
|||||
|
|
|
|
|
|
|
|
|||
|
12 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
Пример 5.3. Найти накопленную стоимость через 10 лет десяти еже-
дневных выплат в размере 1 000 у.д.е, если первая выплата производится в момент t = 0. Сила процента определяется формулой Студли с параметрами р = 0,076 961; r = 0,5; s = 0,121 890.
Решение. Найдём текущую стоимость потока на момент t = 0:
0
A(O) 1 000  V (i).
V (i).
i 0
Сделаем перерасчёт, исходя из формулы (5.11):
|
1 000 |
0 |
||
A(10) |
V (i). |
|||
|
|
|||
V (10) |
||||
|
i 0 |
|||
В случае формулы Студли величина V(t) находится из равенства (3.26):
V (t) |
2 |
(1,22) t |
1 |
|
(1,06) t . |
|
3 |
3 |
|||||
|
|
|
||||
Выполнив расчёты, получим А(10) = 22 622 у.д.е.
5.4. Процентный доход
Рассмотрим задачу, когда инвестор не накапливает капитал, но снимает проценты, оставляя начальную сумму Р неизменной. Пусть вначале инвестор желает получать доход в конце каждого единичного момента времени с фактической процентной ставкой, равной i. В этом случае процентный доход в единицу времени равен рi.
Рассмотрим более сложную ситуацию, когда инвестор вкладывает капитал Р в начальный момент t0 и желает получать проценты до момента времени t в конце каждого интервала длительностью h, где
h = |
t t0 |
, |
n – целое число. Тогда в конце j-гo интервала инвестор будет |
|
n |
||||
|
|
|
получать доход
44

j S P  h
h  ih (t0 ( j i)h), 1
ih (t0 ( j i)h), 1 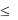 j n .
j n .
Здесь ih (t0 jh) – номинальная процентная ставка на интервале времени от
t0 + (j – 1) до t0 +jh. Сумма S процентного дохода к моменту t будет равна
n |
|
|
(5.13) |
|
S P |
hih (t0 |
jh). |
||
|
||||
j |
1 |
|
|
|
Пусть теперь нам дана сила процента |
t . В этом случае равенство |
|||
(5.13) можно записать в терминах ( t ). |
|
|||
Для этого в (5.13) достаточно перейти к пределу при h → + 0, вос-
пользоваться определением (3.1) для |
t и определением определённого |
интеграла: |
|
|
t |
S(t) P |
( y)dy. |
|
t0 |
Тогда, по определению, норма выплат процентного дохода (t) равна (t) |
|
= =S'(t) = P ( t ), а текущая стоимость на момент процентного дохода от to до t по формуле (5.5) равна
|
|
|
|
t |
|
|
|
|
|
|
A(t) |
P |
|
|
( у)V ( у)dy, |
(5.14) |
|||
|
|
|
|
t0 |
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
(5.15) |
|
V (t) |
exp |
( y)dy . |
|
|
|||||
|
|
|
|||||||
|
|
t0 |
|
|
|
|
|
|
|
Преобразуем формулу (5.14): |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
(5.16) |
A(t) P V ( y)dy |
PV ( y) |
|
t |
|
P(V (t |
0 |
) V (t)). |
||
|
|
|
|||||||
|
|
|
|
t |
0 |
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
так как V(t0) = 1то формула (5.16) принимает вид |
|
||||||||
|
А(t) P 1 V (t) . . |
|
|||||||
45
Найдём текущую стоимость капитала. Так как инвестируемый капитал все время постоянен (процентный доход как бы непрерывно вытекает из банка), то его текущая стоимость А1 (t) равна А1(t) = PV(t).
Тогда сумма текущих стоимостей суммы процентов A(t) и капитала A1
(t) равна первоначальному капиталу A(t) A1 (t) P 1 V (t) PV (t) P, что и должно быть, исходя из интуитивных представлений.
PV (t) P, что и должно быть, исходя из интуитивных представлений.
Интересно отметить, что текущая стоимость суммы процентов A(t)
стремится к Р при t , так как V(t) 0. Теоретически это означает, что
хотя инвестор никогда и не изымает капитал Р, но через достаточно большое время он его получает в виде процентов.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.На какие типы подразделяются потоки наличности?
2.Какими показателями определяется непрерывный поток наличности?
3.Как определяется современная стоимость для дискретных и непрерывных потоков наличности?
4.Каким образом осуществляется пересчёт текущей стоимости потока наличности с одного момента времени на другой?
5.Каким образом вычисляется процентный доход как непрерывный поток наличности, а также его современная стоимость?
6.РЕНТЫ
6.1.Понятие ренты.
6.2.Простая рента пренумерандо.
6.3.Простая рента постнумерандо.
6.4.Общая рента.
46
6.1. Понятие ренты
Финансовые ренты, или аннуитеты, представляют собой частный случай потоков наличности, когда денежные суммы являются поло-
жительными и следуют друг за другом через равные промежутки времени.
Интервал времени между двумя последовательными денежными суммами носит название периода ренты. Существует чрезвычайно большое число рентных схем.
Если денежные суммы (платежи) равны между собой, то рента называется постоянной. Если платежи не равны между собой, то рента называется переменной. В этом случае задается закон изменения платежей.
Ренты различаются также по моменту выплаты платежей. Если платежи происходят в конце каждого периода, то такие ренты назы-
ваются приведёнными, или пренумерандо. Если платежи осуществляются в конце периода, то ренты называются обычными, или постнумерандо.
На практике эти ренты встречаются наиболее часто.
Ренты также подразделяются на верные и условные. Верные ренты предполагают безусловную выплату всех денежных сумм, например, при погашении кредита. Платежи при условных рентах носят вероятностный характер, например, пенсионные платежи, когда время окончания ренты является случайной величиной. Пенсионные ренты также подразделяются на немедленно начинающиеся и отсроченные.
Кроме того, ренты задаются в различных схемах наращения капитала
(простые, сложные и непрерывные проценты).
В настоящем разделе будет рассматриваться схема сложных процентов и простейшие случаи постоянных рент.
47
6.2. Простая рента пренумерандо
Рассмотрим приведённую ренту, или ренту пренумерандо. В качестве периода ренты Т примем одну единицу времени, то есть Т = 1. В качестве схемы наращения капитала примем сложные проценты с процентной ставкой i в единицу времени. Обычно в качестве единицы времени принимается 1 год, такая рента называется простой годовой рентой.
Найдём современную стоимость данной ренты, если срок ренты со-
ставляет п единиц времени, размер каждого платежа равен R. Поток платежей, описывающий ренту, запишем в форме таблицы (таблица 6.1).
Таблица 6.1 – Поток платежей ренты пренумерандо
С1 = |
С 2 = |
… |
С n = |
R |
R |
|
R |
|
|
|
|
t1 = 0 |
t 2 = |
… |
t n = n |
|
R |
|
–1 |
|
|
|
|
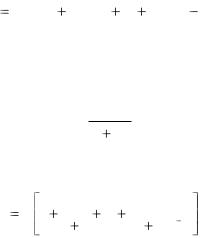
Согласно формуле (5.4), стоимость ренты определяется равенством
A(0) RV (0) RV (1) ... RV (n 1).
В случае сложных процентов дисконтирующий множитель V(t), t –
целое, определяется равенством
V (t) = (1 1i)t .
(6.1)
(6.2)
Подставляя равенство (6.2) в (6.1), получим
A(0) R 1 |
1 |
... |
1 |
. |
(6.3) |
|
|
|
|||
i 1 |
(1 i)(n 1) |
|
Выражение, стоящее в правой части равенства (6.3), представляет собой сумму геометрической прогрессии. Напомним читателю, что гео-
метрической прогрессией называется последовательность а, аq, ..., аqп.
48

При этом сумма Sn первых n + 1 членов геометрической прогрессии определяется равенством
Sn 1 a aq aq 2 ...aq n |
a |
1 |
q n 1 |
. |
(6.4) |
|
|
1 |
q |
|
|||
|
|
|
|
|||
В данном случае a = R, знаменатель прогрессии q задаётся формулой
q |
|
1 |
|
. |
(6.5) |
1 |
i |
|
|||
Равенство (6.3) с учётом формул (6.4) и (6.5) принимает вид
|
1 |
|
|
1 |
|
(6.6) |
||
A(0) R |
(i |
1)n |
|
. |
||||
|
|
|
||||||
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
1 |
i |
|
|
||||
После упрощения формулу (6.6) можно представить в виде:
A(0) R |
1 (1 i) n |
(1 i). |
(6.7) |
i |
|
||
|
|
|
Формулу для современной стоимости простой в единицу времени ренты пренумерандо обычно представляют в форме стандартного меж-
дународного обозначения:
A(0)=R än┐, än┐ = |
1 (i 1)n |
(1 i). |
(6.8) |
i |
|
||
|
|
|
Символ än┐ – общепринятое международное обозначение современной стоимости простой ренты пренумерандо с единичными платежами.
Аналогично можно найти накопленную стоимость А(п) данной ренты на момент времени t = п. Первый член ренты за n единиц времени даёт наращение R(1 + i)n, второй член за n-1 единиц – R(1 + i)n-1 и т.д.,
последний член даёт за 1 единицу времени наращение R(1 + i).
Тогда
A(n) R(1 i)n R(1 i)n 1 ... R(1 i). |
(6.9) |
Суммируя ряд (6.9) по формуле (6.4), получим
49
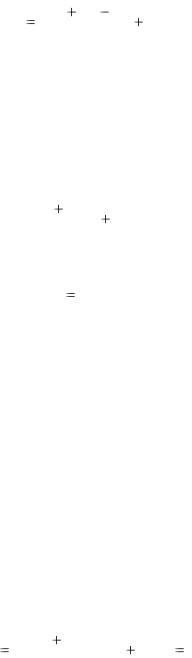
A(n) R |
(1 i)n |
1 |
(1 i). |
(6.10) |
|
i |
|
|
|
||
|
|
|
|
|
|
Накопленную стоимость (6.10) можно получить, пользуясь равен-
ством (5.11). Для этого достаточно равенство (6.7) умножить на ве-
личину (1 + i)n.
Если ввести общепринятое обозначение
|
(1 i)n |
|
|
(1 i), |
|
sn ┐= |
|
|
|
i |
|
то наращенную стоимость можно определить равенством
A(n) Rsn ┐. |
(6.10) |
|
|
Пример 6.1. Клиент банка вкладывает ежегодно в начале каждого года сумму 100 у.д.е. При годовой процентной ставке 8% найти наращение капитала за 10 лет.
Решение. Поток платежей, описывающий отношения клиента и банка,
представляет собой простую годовую ренту пренумерандо, где R = 100, п
= 10, i = 0,08. Накопление капитала на банковском счету клиента к моменту времени t = п представляет собой накопленную стоимость А(п)
данной ренты. Следовательно, в соответствии с формулой (6.10)
наращение капитала за 10 лет определяется равенством
A(10) 100 |
(1 |
0,08)10 |
(1 0,08) 1564,55у.д.е. |
|
0,08 |
||
|
|
|
Пример 6.2. Банк, владеющий участком земли стоимостью 35 000
у.д.е., сдаёт его в аренду фермеру сроком на 10 лет. Определить размер арендного платежа, который производится в начале каждого года,
начиная с даты заключения договора аренды, если годовая банковская процентная ставка равна 9% в схеме сложных процентов.
Решение. Представим поток платежей, описывающий финансовые отношения банка и фермера, в виде таблицы (таблица 6.2).
50
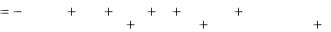
Таблица 6.2 – Поток финансовых отношений фермера и банка
–3500 + |
R |
R |
… |
R + |
|
|
|
|
|
t1 = 0 |
t2 = 1 |
t3 = 2 |
|
t10 = 9 |
Таблица 6.2 составлена со стороны банка, то есть в начальный момент времени банк отдаёт 35 000 у.д.е. (в таблице эта сумма берётся со знаком
"минус") и затем получает арендные платежи в течение 10 лет, а в начале
10-го года получает назад £35 000 (цена земли). Здесь предполагается,
что цена земли при землепользовании не уменьшается. Метод определения регулярного платежа базируется на принципе эквивалентности финансовых обязательств сторон. Этот принцип мате-
матически можно сформулировать как равенство нулю современной стоимости потока наличности, описывающего финансовую операцию.
Данный принцип базируется на интуитивном понятии равенства сторон,
участвующих в сделке, а именно равенстве доходов и расходов одной стороны или, что то же самое, равенстве доходов обеих сторон.
Арифметическое равенство доходов и расходов здесь не годится, так как не учитывается время поступления и расходования денег.
Чтобы объединить факторы времени и денег в формулировании ра-
венства сторон, экономисты договорились привлекать операцию дис-
контирования потока наличности, базирующуюся на математической эквивалентности денег в рамках той или иной схемы наращения капитала.
Принцип финансовой эквивалентности сторон является общепринятым и служит базой расчётов аналогичных задач финансового менеджмента,
будь то ренты, кредитные расчёты, лизинговые операции, ипотеки,
оценка инвестиционных проектов и т.д.
Итак, найдём современную стоимость данного потока наличности на дату заключения договора:
A(0) |
35 000 R(1 |
1 |
... |
1 |
35 000 |
1 |
. |
|
|
|
|
|
|||||
1 i |
(1 i)9 |
_(1 i)9 |
||||||
51
