
5358
.pdf
3.Какой вид имеют соотношения, связывающие номинальные процентные ставки и силу процента, и в чем их экономический смысл?
4.В чём смысл введения в практику силы процента,
определяемой формулой Студли?
4. УЧЁТ ИНФЛЯЦИИ И НАЛОГООБЛОЖЕНИЯ
Процесс инфляции – это обесценивание денег, то есть когда за опре-
делённую совокупность товаров нужно уплатить большую сумму денег,
чем раньше, например, месяц или год назад. Инфляция – это процесс,
который в некотором смысле является обратным наращению капитала. Но как измерить и как её учесть при наращении капитала? Пусть, например, 1 литр молока стоил 12 рублей в начале прошлого года, а в начале следующего стоит 15 рублей. Цена товара возросла в 1,25 раза. Обычно рассматривают не один товар, а набор товаров и услуг, называемый
"рыночной корзиной". Если P(t) – цена рыночной корзины на момент времени t, a P b – цена рыночной корзины в базовом периоде, то величина
J p |
(t) |
P(t) |
(4.1) |
Pb |
|
||
|
|
|
указывает, во сколько раз изменилась цена, и носит название индекса цен.
Темпом инфляции за период Т называют относительное изменение индекса цен за этот период:
hT |
J p (T ) J p (O) |
|
J p (T ) |
1, |
(4.2) |
|
|
|
|
||
J p (O) |
|
J p (O) |
|
||
|
|
|
|
32
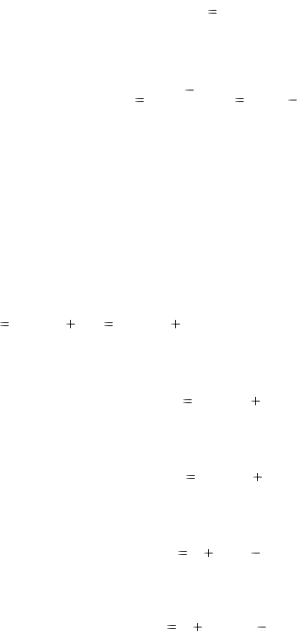
где Jp(0), JP(T) – индекс цен в начале и в конце периода. Величину ht
можно выразить через цену рыночной корзины, представив индекс
J p (0) по формуле (4.1) в виде:
J p |
(O) |
P(O) |
. |
(4.3) |
Pb |
|
|||
|
|
|
|
Подставляя (4.1) и (4.3) в (4.2), получим:
hT |
P(T ) P(O) |
|
P(T ) |
1. |
(4.4) |
P(O) |
|
P(O) |
|
||
|
|
|
|
Из формулы (4.4) следует равенство
(4.5)
которое напоминает наращение денежных сумм по схеме простых про-
центов. Аналогично Jp(T) = Jp(0)(1+hT). Индекс JP(T) является исходным для вычисления индекса в следующем периоде:
J |
p |
(2T ) |
J |
p |
(T )(1 |
h ) |
J |
p |
(O)(1 |
h )2 . |
|
|
|
|
T |
|
|
T |
Через т периодов индекс цен будет равен
J |
p |
(mT ) |
J |
p |
(O)(1 |
h )m . |
(4.6) |
|
|
|
|
T |
|
Темп инфляции за период тТ, по определению, находится из равенства
J p (mT ) |
J p (O)(1 |
hm T ) |
(4.7) |
Из равенств (4.6) и (4.7) следует, что |
|
|
|
h |
(1 h )m |
1. |
(4.8) |
m T |
T |
|
|
На основании формулы (4.8) можно найти hТ:
h |
(1 h |
)1/ m |
1. |
(4.9) |
T |
m T |
|
|
|
Из формулы (4.6) следует, что возрастание индекса цен соответствует закону наращения капитала по сложным процентам.
33
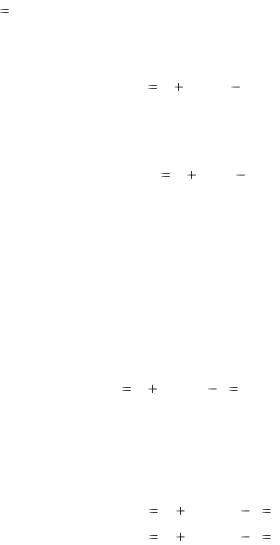
|
Предположим, что известен темп инфляции за |
1 |
часть года, то есть |
||||||||||
|
m |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
и T |
1 |
|
. Тогда годовой темп инфляции h, согласно (4.8), определяется |
||||||||
|
|
|
|||||||||||
1/ m |
|
m |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
равенством |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
h |
(1 |
h |
)m |
1, |
|
(4.10) |
||
|
|
|
|
|
|
|
1/ m |
|
|
|
|
||
|
а темп инфляции за период |
|
1 |
|
– равенством |
|
|
||||||
|
|
m |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
h |
(1 |
|
h)1/ m |
1. |
|
(4.11) |
||
|
|
|
|
|
1/ m |
|
|
|
|
|
|
|
|
Соотношения (4.10) и (4.11) являются аналогами соотношений между эквивалентными процентными ставками.
Пример 4.1. Месячный темп инфляции равен 3 %. Найти: а) годовой, б)
полугодовой; в) квартальный темп инфляции.
Решение. Согласно формуле (4.10), годовой темп инфляции равен
h (1 0,03)12 1 0,42(42%).
Аналогично по формуле (4.11) находятся полугодовой и квартальный темпы инфляции:
h |
(1 |
0,42)1/ 2 |
1 |
0,19(19%), |
1/ 2 |
|
|
|
|
h |
(1 |
0,42)1/ 4 |
1 |
0,09(9%). |
1/ 4 |
|
|
|
|
Рассмотрим денежную сумму S при t = 0 и t = Т в условиях инфляции.
Если Р(0) и Р(Т) – цены рыночной корзины при t = 0 и t= = Т, то цена при t = Т увеличилась по сравнению с ценой при t = 0 в Р(Т)/Р(0) раз,
а соответственно реальная ценность денежной суммы S- покупательная способность – уменьшилась в то же число раз, равное, согласно формуле
(4.5), величине 1 + hT.
Обычно покупательную способность С денежной суммы S соотносят с этой суммой в каждый момент времени t по формуле
34

|
S(t) |
(4.12) |
|
С(t) |
|
. |
|
J p (t) |
|
||
На основании (4.12) покупательную способность денежной суммы можно сравнить в различные моменты времени. Например, для t = 0 и t = Т
имеем
C(T ) |
|
S(t) |
1 |
|
S(t) |
||
|
|
|
|
|
|
|
. |
C(O) |
|
S(O) J p (T ) / J p (O) |
S(O)1 hT |
||||
Если денежная сумма S(t) не претерпевает процесса наращения по
какой-либо схеме, то S(T) = S(0) и, следовательно, |
С(Т ) |
|
1 |
, |
|
С(0) |
1 hT |
||||
|
|
||||
покупательная способность уменьшилась в 1 + hT раз. Пусть сумма S(0)
за время Т наращивается по закону простых процентов с процентной ставкой iT. Тогда S(T) =S(O)(1+i T ) и
С(Т ) |
1 |
iT |
. |
(4.13) |
|
|
|
|
|
||
С(0) |
1 |
hT |
|
||
Равенство (4.13) можно записать в виде
С(Т ) С(О) |
|
1 |
iT |
. |
(4.14) |
1 |
hT |
|
|||
|
|
|
|||
Формула (4.14) показывает изменение покупательной способности денег с учётом инфляции при темпе hT и наращения по простым процентам при процентной ставке iT. Введём реальную процентную ставку (или реальную доходность) rT по формуле
С(T ) |
C(T ) C(O) |
. |
(4.15) |
C(O) |
|
||
|
|
|
Величина rT определяет доходность операции инвестирования в схеме простых процентов при учёте инфляции. Из формул (4.14) и (4.15)
следует соотношение
rT |
|
1 |
iT |
1 |
|
1 |
hT |
||||
|
|
||||
35

или
r |
iT |
hT |
. |
(4.16) |
|
|
|
||
T |
1 |
hT |
|
|
|
|
|
Если период Т равен одному году, то нижний индекс у переменных опускают: h — годовой темп инфляции, i – годовая процентная ставка, rT- –
реальная годовая ставка доходности.
Формула (4.16) опровергает распространённое заблуждение, что ре-
альная ставка доходности равна разности процентной ставки и темпа инфляции.
Пример 4.2. Определить реальную годовую ставку доходности, если годовая процентная ставка 30%, а месячный темп инфляции составляет
2%.
Решение. Найдём вначале по формуле (4.10) годовой темп инфляции:
h (1 0,02)12 1 0,27(27%).
На основании формулы (4.16) можно записать r = |
|
i |
h |
или |
|||||
1 |
h |
||||||||
|
|
|
|
|
|
||||
r |
0,3 |
0,27 |
0,02(2%). |
Обычно инвестор задаётся минимальной |
|||||
|
|
||||||||
1 |
0,27 |
||||||||
|
|
|
|
|
|
|
|||
приемлемой для себя реальной процентной ставкой r, называемой барьерной ставкой, и затем по формуле (4.17) находит минимальную процентную ставку i, начиная с которой имеет смысл инвестировать средства. Искомая величина i определяется равенством
i r h(1 r). |
(4.18) |
Формула (4.18) носит название формулы Фишера. Величина h(1 + r) из формулы (4.18) называется инфляционной премией.
Пример 4.2. Пусть барьерная ставка равна 10%. При годовом темпе инфляции 24% найти минимальную приемлемую процентную ставку инвестирования.
Решение. Согласно формуле (4.18), имеем
36
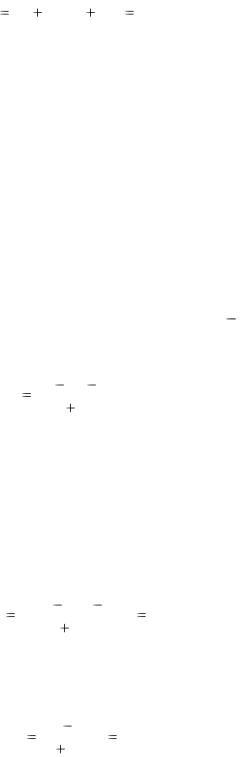
i 0,1 0,24(1 0,1) 0,36(36%).
Исчислим теперь реальную ставку доходности с учётом инфляции и
налогообложения. Пусть ставка налога на прибыль равна f. Тогда при заданной годовой процентной ставке i начальный капитал Р даёт прибыль iР, налог с которой равен сумме iPf. Таким образом, чистая прибыль (за вычетом налога), равна величине iР(1-f). Из последнего выражения следует, что фактическая процентная ставка if с учётом налогообложения определяется равенством
if = i(1 – f). |
(4.19) |
|||
Подставляя в равенство (4.17) вместо i величину i /1 |
f , получим |
|||
реальную годовую ставку доходности: |
|
|||
r |
i(1 |
f ) h |
|
(4.20) |
1 |
h |
|
||
|
|
|||
с учётом инфляции и налога на прибыль.
Пример 4.3. Определить реальную ставку доходности при годовой процентной ставке 50%, годовом темпе инфляции 36% и ставке налога на прибыль 20%.
Решение. Согласно формуле (4.20),
r |
0,5(1 |
0,2) |
0,36 |
0,03(3%). |
|
|
|
||
1 |
0,36 |
|
||
|
|
|
Если бы налог не учитывался, то реальная процентная ставка равнялась бы
r |
0,5 |
0,36 |
0,10(10%). |
|
|
|
|||
1 |
0,36 |
|||
|
|
Таким образом, даже двадцатипроцентный налог на прибыль снизил реальную ставку доходности более чем в три раза. Этот факт объясняется тем обстоятельством, что налог взимается с номинального дохода, а не с реального.
Из равенства (4.20) можно найти номинальную процентную ставку i:
37
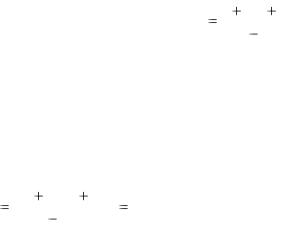
i |
r h(1 r) |
. |
(4.21) |
1 f |
|
||
|
|
|
Пример 4.4. При барьерной ставке 10% годовых, годовом темпе ин-
фляции 30% и налоге на прибыль 25% найти фактическую процентную ставку инвестирования.
Решение. Согласно формуле (4.21) имеем
i |
0,1 |
0,3(1 |
0,1) |
0,57(57%). |
|
|
|
|
|
||
|
1 |
0,25 |
|
||
|
|
|
|
||
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.С помощью какого основного показателя оценивается процесс обесценения денег?
2.Каким соотношением связаны темпы инфляции за различные периоды времени?
3.Каким образом реальная процентная ставка за период времени связана с темпом инфляции и простой процентной ставкой наращения капитала?
4.В чём заключается экономическое содержание формулы Фишера?
5.Каким образом вычисляется реальная процентная ставка с учётом налогообложения?
5. ПОТОКИ НАЛИЧНОСТИ
5.1.Понятие потоков наличности.
5.2.Текущая стоимость потока наличности.
5.3.Оценка текущей стоимости потока наличности.
5.4. Процентный доход.
38
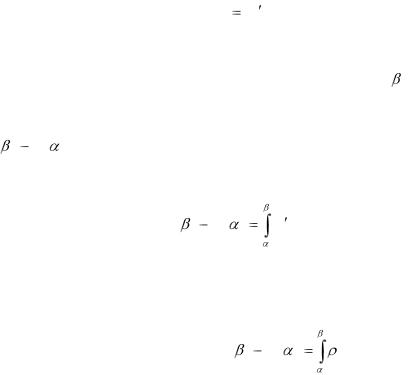
5.1. Понятие потоков наличности
Во многих задачах теории сложных процентов требуется найти те-
кущую стоимость серии будущих выплат (или поступлений). Эти выплаты носят название потоков наличности.
Потоки наличности подразделяются на дискретные и непрерывные.
Под дискретными понимают такие потоки, в которых выплаты (или поступления) денег происходят в фиксированные, отделённые друг от друга интервалами, моменты времени t. Число этих моментов времени может быть как конечными, так и бесконечными.
Иногда удобно рассматривать непрерывные потоки наличности, ко-
торые являются хорошей математической моделью частых выплат,
например, еженедельных пенсий. Непрерывные потоки в момент времени t
характеризуются нормой выплат p(t) в единицу времени.
Функция p(t) определяется следующим образом. Обозначим через Ф(t)
сумму выплат от нулевого момента времени до момента t. Тогда, по определению,
(5.1)
Другими словами, норма выплат – это скорость изменения суммы выплат. Рассмотрим интервал времени от а до . Из экономического смысла функции Ф(t) следует, что сумма выплат в этом интервале равна
Ф ( ) Ф( ) .
Пользуясь определением интеграла, запишем
Ф( ) Ф( ) Ф (t)dt. |
(5.2) |
|
Подставляя в формулу (5.2) формулу (5.1), получим
Ф( ) Ф( ) (t)dt. |
(5.3) |
39

5.2. Текущая стоимость потока наличности
Рассмотрим вначале дискретный поток. Пусть в моменты времени tj
производятся выплаты Cj . Тогда текущая стоимость на момент времени t = 0 этого потока равна
|
w |
|
A(0) |
C j V (t), |
(5.4) |
|
j 1 |
|
где функция V(t) определяется формулой (3.22). В формуле (5.4) w может равняться и бесконечности, тогда нужно потребовать, чтобы ряд в правой части (5.4) сходился.
Рассмотрим непрерывный поток |
наличности с нормой выплат (t). |
|
Рассмотрим интервал времени от t |
до t + t. Тогда сумма выплат равна |
|
t t |
|
|
Sdt |
∆ t. |
|
t
Текущая стоимость этой суммы на момент времени t = 0 равна V ∆t.
Суммируя эту текущую стоимость по всем малым интервалам в пределах от t = 0 до t = Т и заменяя сумму интегралом, получим текущую стоимость потока наличности:
T |
(5.5) |
|
|
A V (t) (t)dt. |
|
t |
|
В формуле (5.5) может быть Т = . Если одновременно имеются как
дискретный, так и непрерывный потоки наличности, то общая текущая стоимость находится по формуле
A(O) |
V (t j )C j |
V (t) (t)dt. |
(5.6) |
|
|||
|
j 1 |
0 |
|
40
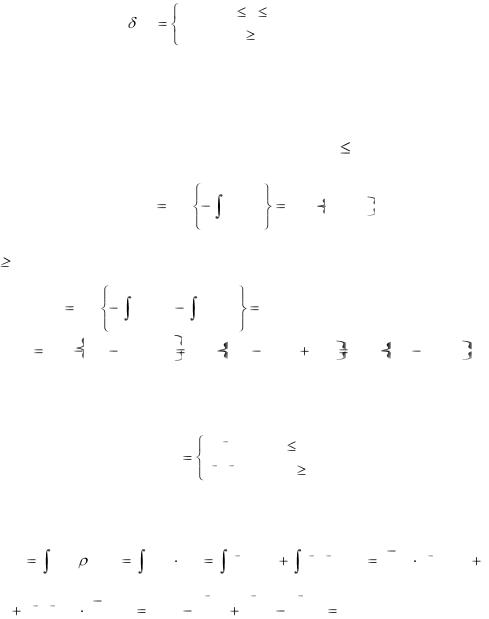
Замечание. Выше предполагалось, что все выплаты являются по-
ложительными, однако можно рассмотреть отрицательные выплаты, то есть когда имеются доходы и расходы. В этом случае чистая текущая стоимость определяется как разность положительного и отрицательного потоков наличности.
Пример 5.1. Пусть |
(t) |
0,04, |
0 |
t 10, |
|
0,03, |
t |
10. |
|||
|
|
Найти V(t) и затем найти текущую стоимость непрерывного потока наличности за 15 лет при норме 1 в год, начиная с момента t = 0.
Решение. По формуле (3.22) найдём V(t) при 0 |
t < 10: |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (t) |
|
exp 0,04dt |
|
|
exp |
0,04t . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При t 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (t) |
exp |
0,04dt |
|
0,03dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
0,4 |
|
0,03t |
|
t |
exp |
0,4 |
0,03t |
0,3 |
exp 0,1 |
0,03t . |
|||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (t) |
|
e 0,04 , |
0 |
|
t 10, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
e 0,1 0,03t , |
|
|
t |
10. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найдём текущую стоимость: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
15 |
|
|
|
|
15 |
|
|
|
10 |
|
|
|
|
15 |
|
|
|
|
1 |
|
|
|
||
A V (t) |
|
(t)dt |
|
V (t) |
1dt |
e 0,04t dt |
|
|
e 0,1 |
003t dt |
|
e 0,04t |
10 |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,04 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
e |
0,1 0,03t |
|
1 |
|
|
|
|
1 |
|
е 0,4 |
|
е 0,4 |
|
|
е |
0,55 |
|
|
11,35 у.д.е. |
|
|
||||
|
15 |
|
|
|
|
|
|||||||||||||||||||
|
0,03 |
|
10 |
0,04 |
0,04 |
0,03 |
|
0,03 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
41
