
5220
.pdf
11
|
|
|
|
y lim |
y |
|
lim |
f (x |
x) |
f (x) |
. |
|
|
|
|
|
x |
|
x |
|
|||||
|
|
|
|
|
x 0 |
x 0 |
|
|
||||
|
|
|
|
Основные правила дифференцирования |
||||||||
Если С – постоянное число, |
U |
U x ,V |
V x |
– функции, имеющие |
||||||||
производные, тогда: |
|
|
|
|
|
|
|
|
|
|||
C |
0 |
|
|
|
(I); |
|
|
|
|
|
||
U |
V |
U |
V |
|
(II); |
|
|
|
||||
C U |
C U |
(III); |
|
|
|
|||||||
U V |
U V |
UV |
|
(IV); |
|
|
|
|||||
U |
|
U V |
UV |
|
(V). |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
V |
|
V |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Если у = f(u), U = φ (х) – дифференцируемые функции от своих аргументов, то производная сложной функции y=f[(φ(x)] существует и равна произведению данной функции по промежуточному аргументу на производную этого аргумента по независимой переменной х, т.е.
|
|
|
|
|
y f (U ) U |
(VI). |
|
|
|
|
|
Формулы дифференцирования основных функций |
|||
1. |
x n |
n x n 1 . |
|
|
|||
2. |
a x |
a x ln a a 0, a 1 . |
|
||||
3. |
e x |
e x . |
|
|
|||
4. |
loga x |
1 |
a 0, a |
1 . |
|||
|
|
|
|
||||
|
|
|
x ln a |
||||
|
|
|
|
|
|
|
|
5. |
ln x |
|
1 |
. |
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
||
6. |
sin x |
|
cos x . |
|
|
||
7. |
cos x |
|
|
|
sin x . |
|
|

12
8. |
tgx |
1 |
|
x |
|
k . |
|
|
|
|
|
||||
|
2 |
|
2 |
||||
|
|
cos |
x |
|
|||
|
|
|
|
|
|||
9. |
ctgx |
1 |
|
|
|
|
x |
|
k . |
|||
|
|
|
|
|
|
|
||||||
sin 2 |
|
|||||||||||
|
|
x |
|
|
|
|
||||||
10. |
arcsin x |
|
|
|
|
1 |
|
|
1 x 1 . |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
1 |
|
|
x 2 |
|||||||||
|
|
|
|
|
|
|
|
|||||
11. |
arccos x |
|
|
|
|
1 |
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
x 2 |
|||||
12. |
arctgx |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
||||
13. |
arcctgx |
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
x 2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1. Найти производные функций: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
a) y |
sin cos 5x ; |
|
b) y |
3 x e3x 5 ; |
c) |
y |
arctg |
. |
|||||||||
|
|
|
|
||||||||||||||
|
1 |
x 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
а) функцию |
можно |
представить в |
виде |
U |
cos 5x . |
Поэтому на |
||||||||||
основании формулы (VI)
y cosU U
cosU U  cos cos 5x
cos cos 5x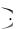 cos 5x
cos 5x
 5sin 5x
5sin 5x  cos cos 5x ;
cos cos 5x ;
b) данная функция представляет произведение двух функций, поэтому на
основании формулы (IV)
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
e3x 5 3e3x |
|
|
|||||
y |
x 3 |
e3x 5 x 3 |
e3x 5 |
3 |
x 3 |
||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
|
e3x |
5 |
3e3x 3 |
|
|
e3x |
5 9e3x |
|
x |
|
e3x 9x |
1 |
5 |
; |
|
|
|||||||||
|
x |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
33 x 2 |
|
|
|
|
|
3 3 x 2 |
|
|
|
|
|
3 3 x 2 |
|
|
||||||||||
2x
c)пусть U 2 . Получим y arctgU . По формулам (V) и (VI)
1 x

13
y |
|
1 |
U |
|
1 |
|
|
|
|
2x 1 x 2 |
|
2x 1 x 2 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
1 U 2 |
|
|
|
2x |
2 |
|
|
|
|
1 x 2 2 |
|
1 2x 2 |
|
x 4 |
4x 2 |
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 2 |
|
|
|
|
|||
|
|
|
|
1 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 1 x 2 |
2x 2x |
|
|
1 x 2 2 |
|
|
2 2x 2 |
|
4x 2 2 2x 2 |
|
2 1 x 2 |
2 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 x |
2 2 |
|
|
1 2x 2 |
|
x 4 |
2 |
2 |
|
1 x |
2 2 |
1 |
x |
2 2 |
|
1 x 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
||||||
Определение 2. Дифференциалом функции у=f(x) называется главная, линейная относительно x часть приращения функции, равная произведению производной на приращение независимой переменной:
dy  f
f  x
x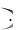 x .
x .
Дифференциал независимой переменной равен приращению этой переменной,
т.е. dx 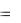 x . Итак, дифференциал функции равен произведению её производной на дифференциал аргумента: dy f
x . Итак, дифференциал функции равен произведению её производной на дифференциал аргумента: dy f 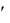 x
x dx .
dx .
Для определения полного дифференциала функции Z=f(x,y) необходимо ввести
понятие частной производной нескольких переменных.
Величина  f x
f x  x, y
x, y  y
y f x, y
f x, y называется полным приращением функции в точке (х,у). Если задать только приращение аргумента х или только приращения аргумента у, то полученные приращения функции соответственно:
называется полным приращением функции в точке (х,у). Если задать только приращение аргумента х или только приращения аргумента у, то полученные приращения функции соответственно:
x Z f x |
x, y |
|
f x, y и |
y Z |
f x, y |
|
y |
f x, y |
||||||
называются частными. |
|
|
|
|
|
|
|
|
|
|||||
Определение 3. Частной производной от функции Z |
|
f |
x, y по |
|||||||||||
независимой переменной х называется конечный предел |
||||||||||||||
Z x |
lim |
x Z |
|
lim |
|
f x |
x, y |
f x, y |
, |
|
||||
x |
|
|
x |
|
|
|||||||||
|
x |
0 |
x |
0 |
|
|
|
|
|
|
||||
вычисленный при постоянном у. |
|
|
|
|
|
|||||||||
Частной производной по у называется конечный предел |
|
|||||||||||||
Z y |
lim |
y Z |
|
lim |
f x, y |
y |
f x, y |
|
, |
|
||||
y |
|
y |
|
|
|
|||||||||
|
y |
0 |
y |
0 |
|
|
|
|
|
|
||||
вычисленный при постоянном х.
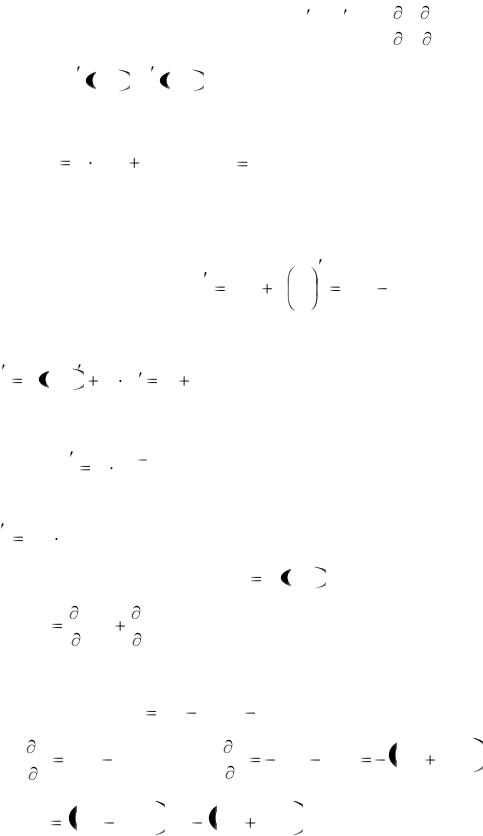
14
Обозначается частная производная так: |
Z x |
, Z y |
|
или |
|
Z |
Z |
|
|||||||||
, |
|
|
|
|
|
, |
|||||||||||
x, |
y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
или f x |
x, y , f y |
x, y . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2. Найти частные производные функций: |
|
|
|||||||||||||||
a) Z x ln y |
y |
; |
b) Z x y |
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение: |
а) при |
|
нахождении частной |
производной |
по х будем |
||||||||||||
рассматривать у как величину постоянную. |
Получим: |
|
|
|
|
|
|
||||||||||
|
|
|
|
Z x ln y |
y |
1 |
|
ln y |
|
y |
. |
|
|
||||
|
|
|
|
x |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично, дифференцируя по у, считаем х постоянной величиной, т.е.
Z y |
|
x ln y |
|
1 |
y |
|
|
|
x |
|
1 |
; |
|
|
|
|
|
||||
|
|
x |
|
|
|
y |
x |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b) |
при фиксированном |
у имеем степенную функцию от х. Таким |
||||||||||||||||||
образом, |
Z x |
|
y |
x y |
1. |
|
|
|
|
|
|
|
|
|
|
||||||
При |
фиксированном |
|
х |
функция |
является |
показательной |
относительно у и |
||||||||||||||
Z y |
|
x y ln x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Полный дифференциал функции Z |
f x, y |
вычисляется по формуле |
|||||||||||||||||||
|
dZ |
|
|
Z |
dx |
|
Z |
dy . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|||||
|
|
Пример 3. |
Найти полный дифференциал функции |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
Z x 4 |
5x 2 y 2 y3 ; |
|
|
|
|||||||||
|
|
Z |
4x3 |
10xy |
|
|
|
|
Z |
5x 2 |
6 y 2 |
5x 2 |
6 y 2 ; |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
y |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dZ |
|
|
4x3 |
10xy |
dx |
|
5x 2 |
6 y 2 dy . |
|
|
||||||||||

15
Общая схема исследования функций и построения графиков
Для полного исследования функции и построения её графика рекомендуется
использовать следующую схему:
1)найти область определения функции;
2)найти точки разрыва функции и вертикальные асимптоты (если они существуют);
3)исследовать функцию на чётность (нечётность) и на периодичность (для тригонометрических функций);
4)найти экстремумы и интервалы монотонности функции;
5)определить интервалы выпуклости (вогнутости) и точки перегиба;
6)исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;
7)найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Исследование функции проводится одновременно с построением её графика.
|
Пример. |
|
Исследовать функцию |
y |
x 4 |
2x 2 |
5 и |
построить |
её |
|||||
график. |
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Область определения |
|
; |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Функция непрерывна во всей её области определения. Следовательно, |
|||||||||||||
нет ни точек разрыва, ни вертикальных асимптот. |
|
|
|
|
|
|||||||||
3. |
Функция чётная, так как |
f |
x |
f x |
: |
|
|
|
|
|
||||
f |
x |
x 4 |
|
2 x 2 |
5 x 4 |
2x 2 |
|
5 f x . |
|
|
|
|||
График функции симметричен относительно оси ординат. |
|
|
||||||||||||
4. |
Экстремумы и интервалы монотонности. |
|
|
|
|
|
||||||||
y |
4x3 |
4x |
4x x 2 |
1 . |
Из |
уравнения |
4x x 2 |
1 |
0 |
получим |
три |
|||
критические точки: |
x1 |
1, |
x2 |
0, |
x3 |
1. Исследуем характер критических |
||||||||
точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0 ; 1), (1; + ∞).

16
На интервалах (-∞; -1) и (0; 1) функция |
убывает, на интервалах |
(-1 ; 0) и |
|||
(1 ; +∞) – возрастает. При |
переходе |
через критические точки |
|
x1 = -1 и х3 = |
|
1 производная меняет знак с минуса на плюс, следовательно, |
в этих точках |
||||
функция имеет минимум. |
ymin f |
1 |
4; ymin f 1 4 . |
При переходе |
|
через критическую точку х = 0 производная меняет знак с плюса на минус.
Следовательно, в |
этой точке |
функция имеет максимум уmax=ƒ(0)=5. |
|
|||||||||||||||||||||||||
5. Интервалы выпуклости и точки перегиба. |
|
|||||||||||||||||||||||||||
y |
|
4x3 |
|
4x |
|
12x 2 |
|
|
4 4 3x 2 |
1 . Из уравнения 4 3x 2 1 |
0 |
|||||||||||||||||
получим |
x1 |
1 |
|
|
0,57 |
|
|
и |
x2 |
1 |
|
0,57 . Определяем знак |
второй |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
3 |
|
3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
производной в каждом из интервалов: |
|
|
|
|
|
|||||||||||||||||||||||
|
; |
|
1 |
|
|
, |
|
|
1 |
|
; |
1 |
|
, |
|
1 |
|
; |
|
|
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3 |
|
|
|
|
|
3 |
|
3 |
|
3 |
|
|
|
|
|
|
||||||||||
Таким |
образом, |
кривая, |
вогнутая |
на |
интервалах |
; |
1 |
и |
1 |
|
; |
и |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
3 |
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
выпуклая на интервале |
|
|
|
|
|
|
1 |
; |
1 |
|
|
, а x |
1 |
|
, x |
|
1 |
|
|
– точки перегиба. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
1 |
|
|
|
|
3 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
2 |
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y |
f |
x |
f |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
4,4 ; |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
1 |
|
|
|
3 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y2 |
f x2 |
|
f |
1 |
|
|
|
|
|
4,4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. Наклонная асимптота имеет вид у = kx + b, если существуют конечные |
||||||||||||||||||||||||||||||||||||||||||||
пределы: k |
lim |
|
f x |
|
|
|
b |
|
|
lim |
f |
x |
k x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
, |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
17 |
|
|
|
k |
lim |
x 4 |
2x 2 |
5 |
lim (x3 |
2x |
5 |
) |
. |
|||
|
|
|
|
|
|
|
||||||
|
x |
x |
|
|
|
x |
|
x |
|
|||
Таким образом, функция не имеет наклонных асимптот. |
||||||||||||
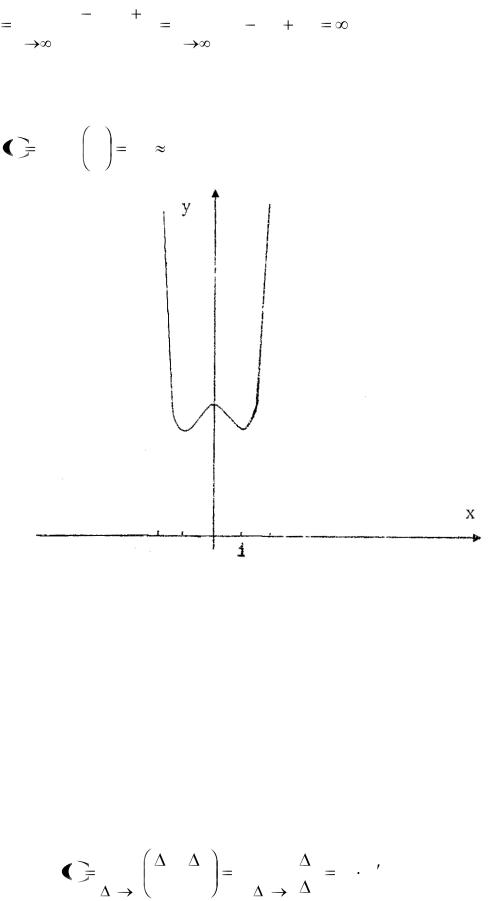
7. Дополнительные точки, уточняющие график: |
|
|||||||||||
f 2 |
13; f |
3 |
|
|
89 |
|
5,6 . Построим график функции: |
|||||
2 |
|
16 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
Применение понятия производной в экономике.
Эластичность функции
Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции.
Определение. Эластичностью функции Ех(у) называется предел отношения относительного приращения функции у к относительному приращению переменной х при ∆х → 0
Ex y |
lim |
y |
: |
x |
|
x |
lim |
y |
|
x |
y . |
(1) |
y |
x |
|
y |
x |
|
y |
||||||
|
x 0 |
|
|
x 0 |
|
|
|

18
Эластичность функции показывает приближенно, на сколько процентов
изменится функция у = f (х) при изменении независимой переменной х на 1%.
Эластичность функции применяется при анализе спроса и потребления. Если
эластичность спроса (по абсолютной величине) |
|
Ex |
|
y |
1, |
то спрос считают |
||||||||||||||||||
|
Ex y |
|
1- |
|
|
|
Ex |
y |
|
|
1– |
|
||||||||||||
эластичным, если |
|
нейтральным, |
если |
|
|
неэластичным |
||||||||||||||||||
относительно цены |
(или дохода). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 1. Рассчитать эластичность функции y |
|
|
x 2 |
3x |
1 и найти |
|||||||||||||||||||
значение показателя эластичности для х = 3. |
По формуле (1) эластичность |
|||||||||||||||||||||||
функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E x y |
|
x |
y |
|
|
|
x |
|
|
2x |
3 |
|
x 2x |
|
3 |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
x |
3x |
1 |
|
|
|
|
|
x |
3x |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть х=3, тогда |
Ex 3 |
y |
1,42 . |
Это |
означает, |
|
что |
|
если |
независимая |
||||||||||||||
переменная возрастет на 1%, то значение |
|
зависимой |
|
переменной |
||||||||||||||||||||
увеличится на 1,42 %. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2. Пусть функция спроса у относительно |
цены |
х |
имеет вид |
|||||||||||||||||||||
y a e 2x , где а |
– постоянный коэффициент. |
Найти значение |
показателя |
|||||||||||||||||||||
эластичности функции спроса при цене х = 3 ден.ед. Рассчитаем эластичность функции спроса по формуле (1)
Ex |
y |
x |
y |
|
x |
|
|
2a e |
2x |
2x . |
|
|
|
|
|
||||||
y |
a |
e |
2x |
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
Полагая х=3 ден.ед., получим |
Ex 3 y |
|
|
6 . Это означает, что при цене х=3 |
||||||
ден.ед. повышение цены на 1% вызовет снижение спроса на 6%, т.е. спрос эластичен.
Интегралы
Определение. Функция F(x) называется первообразной функцией для функции
ƒ(х) на промежутке X, если в каждой точке х этого промежутка
F/ (x) = f(x).

19
Если функция f(x) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причём все первообразные содержатся в выражении
F(x) + С, где С – произвольная постоянная.
Определение. Совокупность всех первообразных функции f(x) на промежутке
X называется неопределённым интегралом от функции f(x) и обозначается  f x dx, т.е.
f x dx, т.е.  f x dx F x
f x dx F x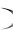 C .
C .
Свойства неопределённого интеграла
1. |
Если a – постоянная величина, то a f |
x dx a |
f x dx . |
|||||||||||||
2. |
|
f1 x |
|
f 2 x |
|
f3 x dx |
f1 x dx |
f 2 x dx |
f3 x dx . |
|||||||
3. |
d[ f x dx] |
f x dx . |
|
|
|
|
|
|||||||||
4. |
|
f |
x dx |
|
|
|
f |
x . |
|
|
|
|
|
|||
5. |
dF x |
|
F x |
C . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Таблица основных интегралов |
|
||||
1. |
0 |
dx |
C . |
|
|
|
|
|
|
|
|
|
||||
2. |
dx |
x |
|
C . |
|
|
|
|
|
|
|
|
|
|||
3. |
|
x k dx |
|
x k |
1 |
|
C |
k |
1, k const . |
|
|
|||||
|
|
k |
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
|
dx |
ln |
|
x |
|
C . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
a x |
|
|
|
|
|
|
|
|
|
||
5. |
a x dx |
|
|
|
C |
|
a |
0, a |
1 . |
|
|
|||||
|
ln a |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
e x dx e x |
C . |
|
|
|
|
|
|
||||||||
7. |
sin xdx |
|
|
cos x |
C . |
|
|
|
|
|||||||
8. |
cos xdx |
|
|
sin x |
C . |
|
|
|
|
|
||||||
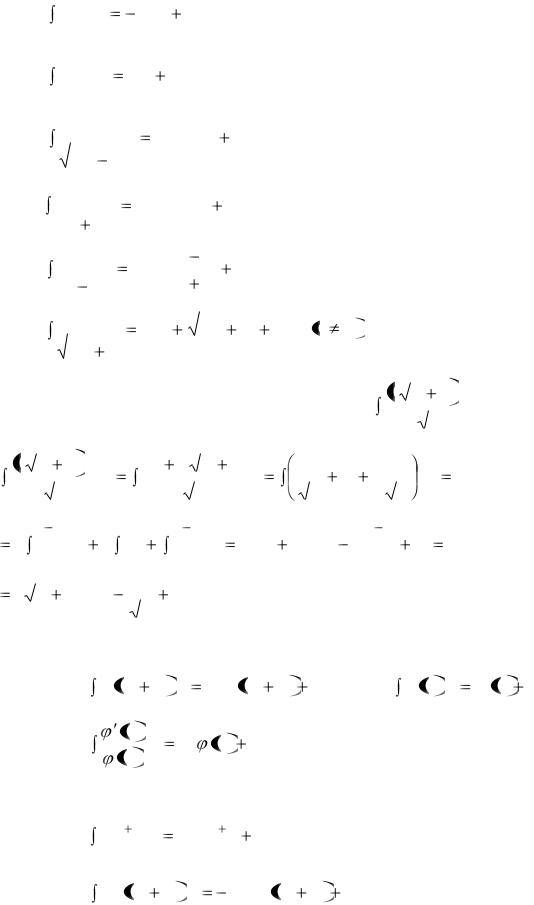
20
9. |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
ctgx |
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
sin |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10. |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
tgx |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11. |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin |
x |
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
a |
2 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12. |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
1 |
|
arctg |
x |
|
|
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
x |
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
13. |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
1 |
|
|
ln |
|
x |
|
|
|
|
|
|
a |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x2 |
|
a2 |
|
|
|
|
|
|
2a |
x |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
x |
|
|
|
|
|
|
|
|
x 2 |
|
a |
|
|
C |
|
|
a |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x 2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
Найти |
|
|
|
|
интеграл |
|
|
2 |
|
|
|
x |
1 |
dx . |
Решение: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
x |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
4x 4 |
|
x 1 |
dx |
|
4 |
|
|
|
|
|
4 |
|
1 |
|
|
|
|
dx |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
x |
x |
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
4 x 2 dx 4 |
|
|
|
x 2 dx 8x 2 |
4 ln |
|
x |
|
2x 2 |
|
|
|
C |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8 x |
|
|
|
|
4 ln |
x |
|
|
|
|
|
|
|
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таблицу интегралов можно расширить, если применить формулы:
а) |
|
f ax |
b dx |
|
|
|
1 |
F ax b |
C , |
если f x dx F x C ; |
||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) |
|
|
dx |
|
ln |
|
|
x |
|
|
|
C . |
|
|
||||
|
|
x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2. Найти интегралы. |
|
|
|
|||||||||||||||
а) |
e |
4x 5 |
dx |
|
1 |
e |
4x |
5 |
|
C ; |
|
|
||||||
|
|
4 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
sin 3x |
2 dx |
|
|
|
|
1 |
cos 3x |
2 |
C ; |
||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
