
5066
.pdf
11
Систему привели к системе с базисом:
|
|
|
11x2 |
|
x4 |
10, |
|
|
x1 |
9x2 |
|
|
8, |
|
|
|
|
x3 |
|
0. |
|
||||||
Базисное решение |
X |
(8, 0, 0, -10) не является опорным. |
||||
Пример 2. Дана каноническая система: |
|
|||||
|
|
x1 |
x2 |
|
3x5 |
2, |
|
|
3x1 |
|
x4 |
x5 |
1, |
|
|
|
x3 |
|
2x5 |
3, |
где x2 , x3 , x4 – базисные неизвестные, свободные члены неотрицательны. Если свободные неизвестные x1 , x5 прировнять к нулю, то получим
базисное неотрицательное решение, которое называется опорным. Итак, X1 (0; 2; 3;1; 0) – опорное решение.
Для нахождения других опорных решений выполняем операцию однократного замещения, при этом:
1)разрешающий столбец выбираем так, чтобы в нем оказался хотя бы один положительный элемент;
2)разрешающую строку выбираем по наименьшему Ө, который равен отношению свободных членов к положительным элементам разрешающего столбца.
Б |
x1 |
x2 |
x3 |
x4 |
x5 |
bi |
Ө |
|
|
|
|
|
|
|
|
x2 |
1 |
1 |
0 |
0 |
-3 |
2 |
2/1=2 |
x4 |
3 |
0 |
0 |
1 |
1 |
1 |
1/3 |
x3 |
0 |
0 |
1 |
0 |
-2 |
3 |
- |
|
|
|
|
|
|
|
|
x2 |
0 |
1 |
0 |
-3 |
-10/3 |
5/3 |
|
x1 |
1 |
0 |
0 |
1/3 |
1/3 |
1/3 |
|
x3 |
0 |
0 |
1 |
0 |
-2 |
3 |
|
X2 (1/ 3; 5 / 3; 3; 0; 0) – опорное решение.
Можно найти и другие опорные решения, например, в качестве разрешающего столбца можно выбрать столбец соответствующий x5 .
Решить системы методом Жордана – Гаусса. Если система имеет множество решений, найти базисное.

|
|
|
|
|
|
12 |
|
|
|
|
|
1. |
x1 |
x2 2x3 1, |
|
2. |
5x1 |
4x2 |
6x3 |
0, |
|
||
3x1 4x2 |
4x3 |
5. |
|
2x1 |
x2 |
3x3 |
2. |
|
|||
|
2x1 |
x2 |
3x3 |
x4 |
1, |
|
5x1 |
2x2 |
x3 |
5, |
|
3. 4x1 |
2x2 |
5x3 |
3x4 |
3, |
4. |
x1 |
x2 |
x3 |
1, |
|
|
|
4x1 |
2x2 |
3x3 |
5x4 |
5. |
|
x1 |
x2 |
x3 |
3. |
|
|
x1 |
x2 |
x3 |
4, |
|
|
3x 2 y |
z |
1, |
|
|
5. |
x1 |
2x2 |
3x3 |
0, |
|
6. 6x 5 y 4z |
2, |
|
|||
|
2x1 |
|
2x3 |
3. |
|
|
9x 8 y 7z |
3. |
|
||
|
x1 |
2x2 |
3x3 |
4x4 |
13, |
|
x1 |
2x2 |
2x3 |
3x4 |
1, |
7. |
x1 |
|
x3 |
2x4 |
1, |
8. |
6x1 |
3x2 |
3x3 |
x4 |
9, |
3x |
4x |
5x |
|
11, |
7x |
x |
x |
2x |
8, |
||
|
1 |
2 |
3 |
|
|
|
1 |
2 |
3 |
4 |
|
|
5x1 |
6x2 |
7x3 |
2x4 |
19. |
|
3x1 |
9x2 |
9x3 |
10x4 |
12. |
Найти все опорные решения следующих систем.
|
x1 |
|
2x4 |
2x5 |
4, |
|
3x1 |
|
|
x4 |
|
1, |
|
|
|
x1 |
|
2x3 |
x5 |
3, |
|||||
9. |
|
x3 |
3x4 |
x5 |
5, |
10. |
|
|||||
|
x2 |
x3 |
|
5, |
||||||||
|
x2 |
|
|
x5 |
2. |
|
|
|||||
|
|
|
|
x1 |
|
|
x3 |
|
x6 4. |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
2x1 |
3x3 |
x4 |
6, |
|
x1 |
2x2 |
x3 |
|
10, |
||
11. |
|
x2 |
x3 |
4, |
12. |
|
||||||
|
4x2 |
x3 |
x4 |
5. |
||||||||
|
3x1 |
|
x3 |
x5 |
2. |
|
||||||
|
|
|
|
|
|
|
|
|
||||
13. |
x1 |
x2 |
x3 |
|
3, |
14. |
x2 |
|
2x3 |
x4 |
2, |
|
2x1 |
x2 |
|
x4 |
4. |
x1 |
|
3x3 |
x4 |
3. |
|||
|
x1 |
|
2x4 |
x5 |
1, |
|
x1 |
|
|
x4 |
3x5 |
18, |
15. |
|
x3 |
x4 |
2x5 |
2, |
16. |
x2 |
|
3x4 |
x5 |
14, |
|
|
x2 |
|
2x4 |
3x5 |
11. |
|
|
x3 |
|
x4 |
3 x5 |
2. |

13
3. ГРАФИЧЕСКИЙ МЕТОД
Графически решаются задачи в стандартной форме, содержащие не более двух переменных; задачи общего вида, в системе ограничений которых не более двух свободных неизвестных.
Рассмотрим примеры.
Пример 1. Решить графически задачу линейного программирования.
Z 3x1 x2 max
x1 |
x2 |
2, |
5x1 |
x2 |
5, |
x1 |
x2 |
8, |
x1 |
|
6, |
x1 |
0, x2 |
0. |
Строим область решений системы ограничений. Для этого последовательно определяем области решений каждого неравенства.
Чтобы найти область решений первого неравенства, строим граничную прямую x1 x2 2 , которая делит плоскость на две полуплоскости, а затем, испытывая какую-либо точку (проще О(0;0)), определяем полуплоскость, точки которой удовлетворяют неравенству. Точка О(0;0) не удовлетворяет неравенству x1 x2 2 , следовательно, область решений неравенства не включает начала координат. Отмечаем область стрелками.
Решаем аналогично остальные неравенства, находим общую область решений, удовлетворяющую всем неравенствам.

14
Областью решений системы неравенств является многоугольник
АВСДЕМ. Так как решения удовлетворяют условиям x1 |
0, x2 0 , область |
решений называется допустимой областью решений задачи. |
|
В этой же системе координат строим целевой |
вектор n (3,1) , |
перпендикулярный к линиям уровня Z 3x1 x2 . Строим перпендикулярно вектору линию уровня и, перемещая ее параллельно самой себе в направлении вектора n , определим крайнюю точку области, в которой Z примет наибольшее значение.
В решаемой задаче максимальное значение Z будет достигнуто в точке Е. Определяем координаты этой точки:
x1 |
x2 |
8, |
Е(6; 2), |
x1 |
6, |
|
|
|
|
||
Zmax |
3 6 |
2 20 . |
|
Пример 2. Решить графически:
Z 2x1 4x2 x3 5x4 max
x1 |
x2 |
x3 |
x4 |
5, |
x1 |
x2 |
x3 |
3x4 |
7, |
x j |
0, j |
1,...,4. |
|
|
Приводим систему к системе с базисом:
Б |
|
x1 |
x2 |
|
x3 |
x4 |
bi |
|
|
1 |
1 |
|
1 |
1 |
5 |
|
|
1 |
1 |
|
-1 |
3 |
7 |
x1 |
|
1 |
1 |
|
1 |
1 |
5 |
|
|
0 |
0 |
|
-2 |
2 |
2 |
x1 |
|
1 |
1 |
|
2 |
0 |
4 |
x4 |
|
0 |
0 |
|
-1 |
1 |
1 |
|
x1 |
x2 |
2x3 |
4, |
|
|
|
|
|
|
x3 |
x4 1. |
|
|
|
Перейдем от канонической системы к стандартной, отбрасывая в уравнениях базисные переменные.

15
x2 2x3 4, x3 1.
Исключаем базисные переменные из выражения для функции Z
x1 |
4 |
x2 |
2x3 , |
x4 |
1 |
|
x3 , |
Z 8 2x2 4x3 |
4x2 |
x3 |
5 5x3 13 2x2 2x3 . |
Решаем графически задачу:
Z 13 2x2 2x3 max x2 2x3 4,
x3 1, x2 0, x3 0.
Максимальное значение функции Z достигается в точке А(4;0):
Zmax 13 8 21.
Найдем оптимальное значение x1 , x4 :
x1 |
4 4 0, |
x4 |
1. |
Ответ: Zmax 21, X (0, 4, 0,1) .
Решить графически следующие задачи линейного программирования:
1. Z x1 |
x2 |
max |
2. Z x1 x2 |
max |
|
x1 |
2x2 |
10, |
2x1 |
x2 |
2, |
x1 |
2x2 |
2, |
x1 |
x2 |
5, |
2x1 |
x2 |
10, |
x1 |
2x2 |
2, |
x1 |
0, x2 |
0. |
x1 |
0, x2 |
0. |

3. |
Z |
5x1 |
|
3x2 |
min |
|
3x1 |
|
2x2 |
6, |
|
|
2x1 |
|
3x2 |
6, |
|
|
x1 |
|
x2 |
4, |
|
|
4x1 |
|
7x2 |
28, |
|
|
x1 |
0, x2 |
0. |
||
5. |
Z |
7x1 2x2 min |
|||
|
5x1 |
|
2x2 |
3, |
|
|
|
x1 |
|
x2 |
1, |
|
|
3x1 |
|
x2 |
3, |
|
2x1 |
|
x2 |
4, |
|
|
x1 |
0, x2 |
0. |
||
7. |
Z |
2x1 |
x2 |
min |
|
|
7x1 |
|
5x2 |
28, |
|
|
5x1 |
|
4x2 |
7, |
|
|
|
x1 |
|
2x2 |
5, |
|
x1 |
0, x2 |
0. |
||
9. |
Z |
7x1 |
x2 |
min max |
|
x1 x2 3, 5x1 x2 5, x1 5x2 4, x1 4, x2 4.
11. Z x1 |
3x2 |
min |
x1 |
x2 |
3, |
4x1 |
x2 |
4, |
3x1 |
2x2 |
24, |
5x1 |
4x2 |
20, |
|
x2 |
6, |
x1 |
0, x2 |
0. |
16
4. Z |
x1 |
2x2 |
min |
2x1 |
x2 |
14, |
|
3x1 |
2x2 |
9, |
|
3x1 |
4x2 |
27, |
|
x1 |
0, x2 |
0. |
|
6. Z |
x1 |
x2 |
max |
x1 |
2x2 |
4, |
|
5x1 |
2x2 |
10, |
|
4x1 |
3x2 |
12, |
|
7x1 |
4x2 |
28, |
|
x1 |
0, x2 |
0. |
|
8. Z |
x1 |
x2 |
max |
3x1 |
x2 |
8, |
|
x1 |
2x2 |
6, |
|
x1 |
x2 |
3, |
|
x1 0, x2 0.
10. Z |
2x1 |
2x2 |
max |
||
3x1 |
2x2 |
6, |
|||
|
x1 |
|
x2 |
3, |
|
|
x1 |
|
|
3, |
|
|
|
x2 |
5, |
|
|
|
x1 |
0, x2 |
0. |
|
|
12. Z |
7x1 |
2x2 |
max |
||
|
x1 |
x2 |
5, |
|
|
2x1 |
3x2 |
6, |
|
||
3x1 |
|
x2 |
3, |
|
|
|
x1 |
|
x2 |
2, |
|
|
x1 |
|
x2 |
3, |
|
x1 |
0, x2 |
0. |
|
||

17
13. Z |
4x1 |
3x2 |
x4 |
x5 |
max |
14. Z |
x1 |
2x3 x5 |
min |
|||
x1 |
x2 |
x3 |
x4 |
x5 |
5, |
2x1 |
x2 |
x3 |
1, |
|||
x1 |
3x2 |
x4 |
13, |
|||||||||
|
x2 |
x3 |
x4 |
|
x5 |
2, |
||||||
|
|
4x1 |
x2 |
x5 |
26, |
|||||||
|
|
x3 |
x4 |
x5 1, |
||||||||
|
|
x1 |
3x2 |
|
x6 0, |
|||||||
x j |
0, |
j |
1,...,5. |
|
|
|
||||||
|
|
x j |
0, |
j |
1,...,6. |
|
||||||
|
|
|
|
|
|
|
|
|||||
15. Изготовление продукции двух видов требует использования сырья трех видов. Запасы сырья, норма расхода и прибыль от реализации единицы продукции приведены в таблице:
Вид |
Запас |
|
Норма расхода |
|
сырья |
сырья |
P1 |
|
P2 |
S1 |
120 |
3 |
|
2 |
S 2 |
40 |
1 |
|
0 |
S3 |
30 |
0 |
|
1 |
|
|
|
|
|
Доход от реализации одного изделия |
3 |
|
2 |
|
Составить план производства, обеспечивающий наибольшую прибыль.
16. Человек должен потреблять в сутки некоторое количество питательных веществ. Их содержание в разных видах пищи приведено в таблице:
|
|
Виды пищи |
||
Питательные |
Норма |
|
|
|
А |
Б |
|||
вещества |
|
|||
|
|
|
||
Жиры |
10 |
1 |
5 |
|
Белки |
12 |
3 |
2 |
|
Углеводы |
16 |
2 |
4 |
|
Стоимость 1 усл. ед. вида |
2 |
3 |
||
пищи |
|
|||
|
|
|
||
Составить диету наименьшей стоимости при условии, что организм должен получить минимальную суточную норму питательных веществ.
4. СИМПЛЕКСНЫЙ МЕТОД
Если система ограничений основной задачи каноническая, то задачу линейного программирования можно решить симплексным методом.
Пример 1. Решим задачу симплекс-методом:

|
18 |
|
Z x1 |
6x2 |
max |
x1 |
x2 |
6, |
x1 |
2x2 |
4, |
2x1 |
x2 |
4, |
x1 |
0, x2 |
0. |
Преобразуем стандартную задачу в основную, добавляя к левым частям ограничений балансовые переменные. Целевая функция при этом не изменится.
Z x1 |
6x2 |
|
max |
|
|
x1 |
x2 |
|
x3 |
6, |
|
x1 |
2x2 |
|
|
x4 |
4, |
2x1 |
x2 |
|
|
x5 |
4, |
|
|
|
|
|
|
x j |
0, j |
1,5. |
|
||
Получим каноническую задачу. Неизвестные x3 , x4 , x5 – базисные, x1 , x2 – свободные. Можно записать исходное опорное решение: X 0; 0; 6; 4; 4 .
Составим симплексную таблицу:
Cj |
Базис |
0 |
C1=1 |
C2=6 |
C3=0 |
C4=0 |
C5=0 |
θ |
|
базиса |
ai 0 |
x1 |
x2 |
x3 |
x4 |
x5 |
|||
|
|
||||||||
0 |
x3 |
6 |
1 |
1 |
1 |
0 |
0 |
6 |
|
0 |
x4 |
4 |
1 |
-2 |
0 |
1 |
0 |
- |
|
0 |
x5 |
4 |
-2 |
1 |
0 |
0 |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
Z = |
0 |
-1 |
-6 |
0 |
0 |
0 |
|
|
0 |
x3 |
2 |
3 |
0 |
1 |
0 |
-1 |
2/3 |
|
0 |
x4 |
12 |
-3 |
0 |
0 |
1 |
2 |
- |
|
6 |
x2 |
4 |
-2 |
1 |
0 |
0 |
1 |
- |
|
|
Z = |
24 |
-13 |
0 |
0 |
0 |
6 |
|
|
1 |
x1 |
2/3 |
1 |
0 |
1/3 |
0 |
-1/3 |
|
|
0 |
x4 |
14 |
0 |
0 |
1 |
1 |
1 |
|
|
6 |
x2 |
16/3 |
0 |
1 |
2/3 |
0 |
1/3 |
|
|
|
Z = |
98/3 |
0 |
0 |
13/3 |
0 |
5/3 |
|
Cj – коэффициенты целевой функции. При х1 коэффициент C1=1, при х2 – C2=6, неизвестные х3, х4, х5 отсутствуют в целевой функции, следовательно их коэффициенты равны нулю. В первом столбце таблицы записываются коэффициенты целевой функции, соответствующие базисным неизвестным второго столбца таблицы.

19
Алгоритм симплекс-метода
1.Записываем данную задачу в исходную симплекс-таблицу.
2.Если все элементы оценочной строки симплексной таблицы неотрицательны, то исходный план является оптимальным.
3.Если в оценочной строке содержится отрицательный элемент, над которым в таблице нет положительных элементов, то целевая функция не ограничена сверху и задача не имеет решения.
4.Если над каждым отрицательным элементом оценочной строки в соответствующем столбце есть хотя бы один положительный элемент, то можно перейти к лучшему плану.
С этой целью:
а) выбираем в исходной таблице разрешающий столбец. Это столбец, соответствующий наименьшей отрицательной оценке. Пусть это столбец, соответствующий переменной xp ;
б) выбираем разрешающую (q-тую) строку из условия
aq0 |
min |
ai0 |
, |
a |
|
0, |
(i 1,2,..., m); |
|
aqp |
aip |
ip |
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
в) элемент aqp – разрешающий;
г) элементы разрешающей строки делим на разрешающий элемент; д) элементы остальных строк вычисляем по правилу «прямоугольника»; е) элементы оценочной строки также вычисляются по правилу
нахождения оценок. Эту формулу можно использовать в качестве контроля вычислений.
Правило нахождения оценок
Оценка для хj равна сумме произведений элементов данного столбца на соответствующие элементы первого столбца (Сj-базисные) минус Сj данного столбца (коэффициент над хj).
Например, в первой части таблицы оценка при х2 равна:
1 0
0 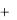 2
2  0 1
0 1 0 6
0 6 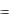 6 ,
6 ,
в третьей части таблицы оценка при х3 равна:
1/ 3 1 1
1 1 0 2 / 3
0 2 / 3 6 0 13/ 3.
6 0 13/ 3.
Значение целевой функции при данном базисе подсчитывается по правилу нахождения оценок. Так, в третьей части таблицы
2 / 3 1 14
1 14 0 16/ 3
0 16/ 3 6 0 98/ 3.
6 0 98/ 3.
При решении задачи на максимум опорный план будет оптимальным, если все оценки будут неотрицательными. Исходный опорный план

20
X 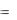 0; 0; 6; 4; 4
0; 0; 6; 4; 4 не будет оптимальным, т.к. оценки при х1 и х2 – отрицательные.
не будет оптимальным, т.к. оценки при х1 и х2 – отрицательные.
По наименьшей отрицательной оценке выбираем разрешающий столбец (столбец х2). Можно перейти к лучшему опорному плану методом однократного замещения, если в этом столбце есть хотя бы один положительный элемент. В нашем примере это условие выполняется. Теперь необходимо выбрать разрешающую строку.
Разрешающую строку определяем по наименьшему θ, равному отношению свободных членов ( ai 0 ) к соответствующим положительным
элементам разрешающего столбца. В разрешающем столбце х2 два положительных элемента. Находим отношения:
a10 : a12 |
6 :1 |
6, |
a30 : a32 |
4 :1 |
4. |
Наименьшим отношением является |
отношение a30 : a32 , следовательно, |
|
a32 =1 – разрешающий элемент. Неизвестное х2 входит в базис вместо х5. Т.о. посредством преобразования однократного замещения мы перешли к лучшему опорному плану X 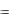 0; 4; 2;12;0 , при котором Z 24 . Но этот план также не является оптимальным, т.к. при х3 оценка отрицательная. В третьей части таблицы получен оптимальный план (нет отрицательных
0; 4; 2;12;0 , при котором Z 24 . Но этот план также не является оптимальным, т.к. при х3 оценка отрицательная. В третьей части таблицы получен оптимальный план (нет отрицательных
оценок): X опт. 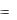 2 / 3;16/3;0;14; 0 , Zmax 98/ 3.
2 / 3;16/3;0;14; 0 , Zmax 98/ 3.
Замечание 1. Оценки и значение целевой функции, начиная со второй части таблицы, следует для контроля считать и по правилу нахождения оценок, и по правилу прямоугольника.
Замечание 2. Если в столбце с отрицательной оценкой нет положительных элементов, то задача оптимального решения не имеет, а целевая функция на множестве допустимых решений неограниченна
( Z 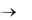 ).
).
Замечание 3. Если требуется найти минимум функции
Z |
c1 x1 |
c2 x2 |
... |
cn xn , |
то можно перейти к задаче максимизации функции |
||||
Z1 |
Z |
c1 x1 c2 x2 |
... |
cn xn max . |
Замечание 4. Признаком альтернативного оптимума задачи является наличие нулевой оценки при свободном неизвестном оптимальной таблицы. В задаче с альтернативным оптимумом необходимо найти
