
4927
.pdf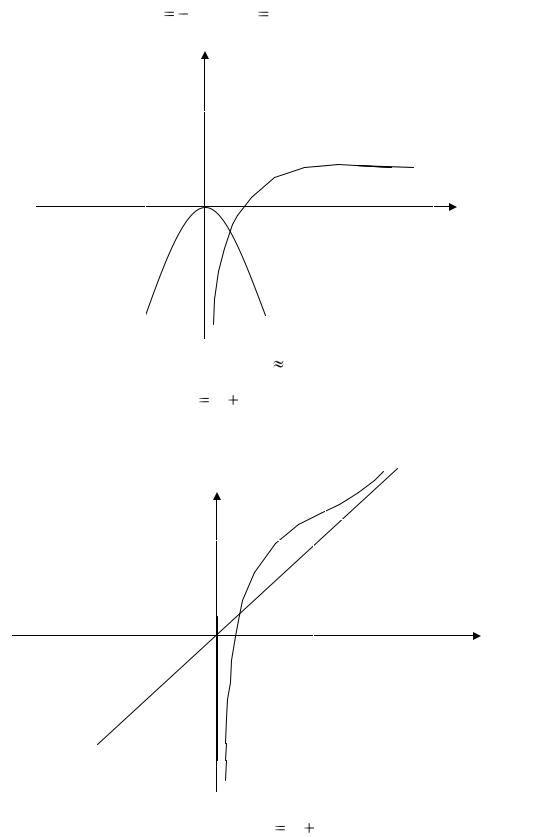
11
Решим это уравнение графически. Построим в прямоугольной системе
координат графики функций |
y |
x 2 и y |
2 |
ln x . |
|
1 |
|
|
у
|
|
|
y2 = lnx |
0 |
1 |
|
х |
|
|
K |
|
|
|
|
|
|
|
|
|
y1 = -x2 |
Получили точку К, |
абсцисса этой точки x |
0,6 , поэтому искомая точка |
|||
пересечения графика |
функции |
y x |
|
ln x |
с осью Ох будет иметь |
|
|
||||
|
x |
||||
|
|
|
|
|
|
координаты (0,6; 0), обозначим эту точку В(0,6; 0). |
|||||
График функции изображен на рис. 3. |
|
|
|
||
|
|
|
у |
A |
|
O |
х |
B
y = x
Рис. 3. График функции y x |
ln x |
. |
|
||
|
x |
|
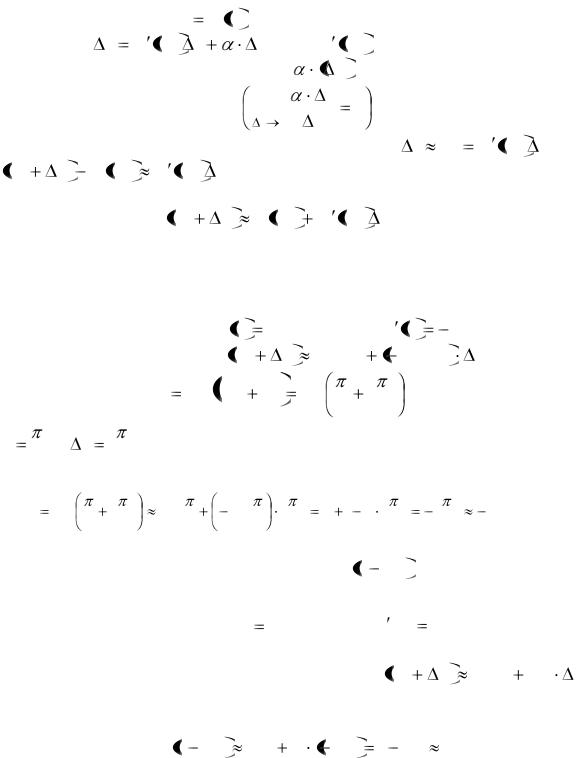
12
2. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛА
|
Приведем основные формулы, которые используются в |
||||||||||||||
приближенных вычислениях с помощью дифференциала. |
|
|
|
||||||||||||
|
Если |
функция |
y |
f x |
дифференцируема |
в |
точке |
х0, |
то |
её |
|||||
приращение |
y |
f x0 |
x |
|
x , где |
f |
x0 |
- производная функции в |
|||||||
точке х0, ∆х – приращение аргумента, |
|
x - бесконечно малая величина |
|||||||||||||
более высокого порядка чем ∆х |
lim |
|
x |
0 . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
||
|
Отсюда следует |
приближенное |
равенство |
y |
dy f |
x0 |
x |
или |
|||||||
f x0 |
x |
f x0 |
f x0 |
x. |
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, справедливо приближенное равенство |
|
|
|
|||||||||||
|
|
|
f x0 |
x |
f x0 |
f |
x0 |
x . |
|
(2.1) |
|
|
|
||
Данное равенство тем точнее, чем меньше ∆х.
|
Пример 1. Вычислить приближенно Cos 91°. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим функцию f |
x |
|
cos x , найдем f |
|
|
x |
|
|
|
|
sin x . |
|
|
||||||||||||||||||||||||
Согласно равенству (2.1), Cos x0 |
|
|
|
x cos x0 |
|
|
|
|
sin x0 |
x . |
|
|
||||||||||||||||||||||||||
Учитывая, что Cos 91 |
cos 90 |
1 |
|
|
cos |
|
|
|
|
|
|
, |
возьмем |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|||||
x0 |
|
и x |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда имеем конечный результат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Cos 91 |
cos |
|
|
|
|
|
|
cos |
|
|
sin |
|
|
|
|
|
|
|
0 ( 1) |
|
|
|
|
|
|
|
|
|
|
|
0,017 . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
180 |
|
|
2 |
|
|
2 |
|
180 |
|
|
|
|
180 |
|
|
|
180 |
|
|
|
|
|||||||||||||
|
Пример 2. Вычислить приближенно ln e |
0,1 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим функцию f (x) |
|
ln x , найдем |
|
f |
(x) |
|
|
1 |
. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||
|
Согласно |
|
|
|
|
равенству |
|
|
(2.1), |
|
|
|
ln x0 |
|
|
|
x |
ln x0 |
1 |
x . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За х0 возьмем е, за ∆х – (-0,1), тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ln e |
0,1 |
ln e |
1 |
|
|
0,1 |
1 |
0,1 |
0,963. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
e |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример 3. В результате наблюдений было установлено, что размер |
|||||||||||||||||||||||||||||||||||||
вклада |
клиента |
Сидорова |
в |
|
|
банке |
|
изменяется |
по |
закону |
||||||||||||||||||||||||||||

|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
15x3 |
2x2 |
3x |
11, |
где |
х |
– время в месяцах. |
Найти |
приблизительно |
||||||||
размер вклада через 3,008 месяца. |
|
|
|
|
|
|
|
|
||||||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся приближенной формулой |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
T |
f (x0 ) |
f (x0 ) x , |
|
|
|
|||
где |
Т – |
вклад; |
х0 |
|
= |
3; |
∆х |
= |
0,008; |
T |
f (3) f |
(3) 0,008; |
||||
f (x) 45x 2 |
4x 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда размер вклада примерно равен: |
|
|
|
|
|
|
|||||||||
|
T |
15 |
33 |
2 |
32 |
3 |
3 |
11 |
(45 |
32 |
4 |
3 |
3) |
0,008 |
410,168. |
|
3. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ НА ОТРЕЗКЕ
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего
значений функции на промежутке Х. |
|
|
|
|
Для отыскания наибольшего и наименьшего значений на |
отрезке |
|
рекомендуется пользоваться следующей схемой: |
|
|
|
1. |
Найти производную f (x) . |
|
|
2. |
Найти критические точки функции, в которых |
f (x) 0 |
или не |
существует.
3.Найти значения функции в критических точках, входящих в отрезок, а
также на концах заданного отрезка и выбрать из них наибольшее fнаиб = М и наименьшее fнаим = m.
|
Пример 1. Найти |
наибольшее и наименьшее значения функции |
||||||
y |
|
2x |
на отрезке [0;2]. |
|||||
|
|
|||||||
1 x 2 |
||||||||
|
|
|
|
|
|
|||
|
Решение |
|
|
|
|
|||
|
f (x) |
2 1 x 2 2x 2x 2 2x 2 |
||||||
1. |
|
|
|
|
. |
|||
1 x 2 2 |
|
1 x 2 2 |
||||||
2. |
f (x) |
0, откуда критические точки х1 = 1; х2 = -1. |
||||||
3. |
Критическая точка х2 |
= -1 не принадлежит [0;2]. Значения функции в |
||||||
критических точках и на концах отрезка |
f 0 |
0 , f 1 1 и f 2 |
4 |
. |
|
5 |
|||||
|
|
|
|
||
Итак, M fнаим f (1) 1, m fнаим |
f (0) |
0 . |
|
|
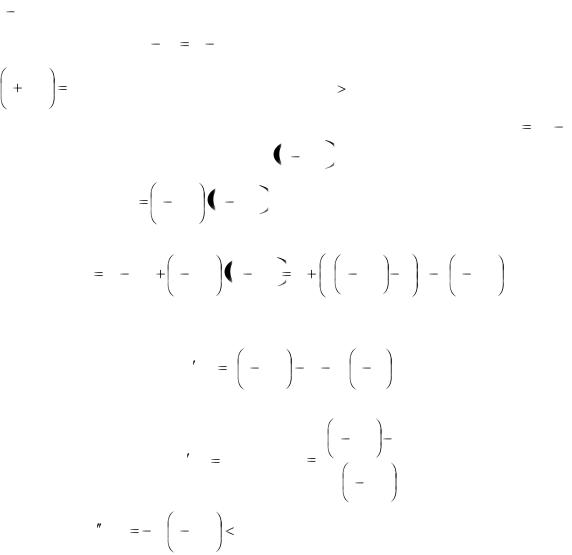
14
Для решения текстовой задачи на нахождение наибольшего (наименьшего) значения функции следует исходя из её условия: выбрать независимую переменную, установить границы ее изменения (промежуток изменения) и выразить исследуемую величину через эту переменную как функцию. Затем проводится исследование этой функции на экстремум и по известному правилу находится наибольшее (наименьшее) значение. Результат анализируется на основании данных задачи.
Пример 2. Капитал в 1 млрд руб. может быть размещен в банке под 50% годовых или инвестирован в производство, причем эффективность вложения в производство ожидается в размере 100%, а издержки задаются квадратичной зависимостью. Прибыль облагается налогом в р%. При каких значениях р вложение в производство является более эффективным, нежели чистое размещение капитала под проценты в банке?
Решение. Пусть х (млрд руб.) инвестируется в производство, тогда (1 х) - размещаются под проценты в банк. Размещенный капитал через год
станет равным 1,5(1 |
x) |
3 |
|
|
3 x , а капитал, вложенный в производство, - |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x 1 |
|
100 |
2x . Издержки составят ax2 , где a |
0 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
100 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Тогда прирост денежной массы от вложения в производство C 2x ax2 . |
|||||||||||||||||||||||||||||
Так как налог на прирост равен |
2x |
ax2 |
|
p |
|
, то прибыль от вложения в |
||||||||||||||||||||||||
100 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
производство Q(x) |
1 |
|
p |
2x ax2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Общая сумма прибыли через год определяется функцией |
|
||||||||||||||||||||||||||||
|
|
|
Q(x) |
3 3 x 1 |
|
|
p |
|
|
2x ax2 |
3 |
2 1 |
|
|
p |
|
|
3 |
x a 1 |
|
p |
x2 . |
||||||||
|
|
|
100 |
|
|
100 |
|
2 |
100 |
|||||||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
|
Найдем максимальное значение этой функции на отрезке [0;1]. |
|||||||||||||||||||||||||||||
|
Вычислим производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
Q (x) 2 1 |
p |
3 |
|
2a 1 |
p |
х. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
100 |
|
2 |
|
x |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приравняем ее к нулю и найдем значение х:
|
|
|
|
|
2 1 |
p |
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Q (x) |
0 при |
x |
100 |
|
|
2 |
. |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
0 |
|
|
p |
|
|
|
|||
|
|
|
|
|
2a 1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
100 |
|
|
|
|||||
Так как Q (x0 ) 2a 1 |
|
p |
0 , то х0 – точка максимума. |
||||||||||
|
|
||||||||||||
100 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
15 |
Теперь |
найдем значение р, если x0 [0;1] . Решив неравенство |
||||
0 2 1 |
|
p |
3 |
1, получим р<25. |
|
|
|
|
|
||
100 |
|
2 |
|||
Таким образом, если р>25, то выгоднее ничего не вкладывать в производство и разместить весь капитал в банк. Если р<25, то прибыль А больше, если деньги будут инвестированы в производство.
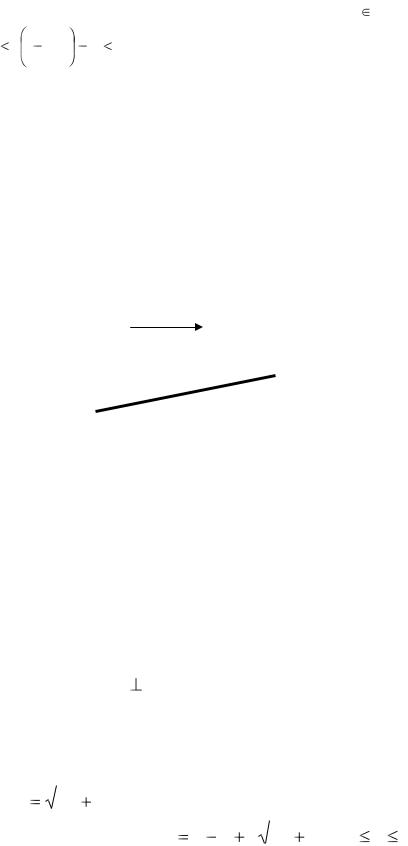
Пример 3. По прямой АВ (см. рис.4) проходит железнодорожный путь. В стороне на расстоянии s от пути находится пункт С, из которого следует перевести груз в пункт А. Предположим, что из пункта С можно добраться по прямой до произвольной точки железной дороги.
|
В |
х |
М |
r – x |
А |
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
С
Рис. 4
По какой трассе следует перевезти груз из пункта С до железной дороги, а затем по железной дороге до пункта А, чтобы транспортные расходы были минимальными, если известно, что издержки по перевозке 1 тонны груза автотранспортом в 3 раза выше, чем издержки при перевозке по железной дороге на такое же расстояние, а также если транспортные расходы пропорциональны расстоянию? Вычислить минимальные транспортные издержки по полученной трассе.
Решение
Проведем [CB] [BA]. Пусть |ВА| = r. Предположим, что мы перевозим груз автотранспортом от С до М – какого-либо пункта на железной дороге. Введем обозначение |ВМ| = х.
Если груз необходимо перевезти по железной дороге на расстояние r от
пункта |
В, |
то путь по железной |
дороге составит r-x. Так как |
|||||
|
|
|
|
|
|
|
|
|
|
CM |
|
s 2 |
x 2 , транспортные расходы составляют: |
||||
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y r x 3 s 2 |
x 2 , 0 x r . |
||
Найдем, при каком значении х транспортные расходы будут минимальными. Для этого найдем наименьшее значение полученной выше функции на отрезке [0;r].
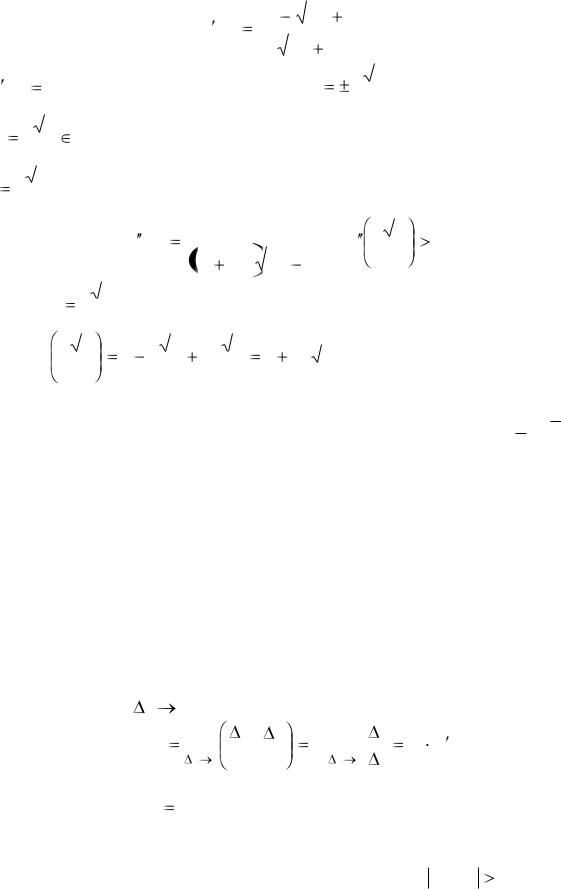
16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
3x |
|
|
|
s 2 |
x 2 |
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 2 |
|
|
|
x 2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f |
(x) |
|
|
0, откуда критические точки |
x |
|
|
|
|
|
|
|
s |
2 |
, но из этих точек лишь |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
s |
2 |
|
|
|
[0; r] , |
|
поэтому |
|
экстремум |
функции |
может |
|
быть только при |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
|
s |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3s 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y (x) |
|
|
|
|
|
|
|
|
|
|
|
|
; |
y |
s 2 |
0 |
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
2 |
x |
2 |
|
s |
2 |
|
|
x |
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
т.е. при x |
|
|
s 2 |
|
функция транспортных расходов имеет минимум. Найдем |
||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
s |
2 |
|
|
|
|
|
|
|
s 2 |
|
|
9s |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
его |
|
y |
|
|
|
|
|
r |
|
|
|
|
r |
|
|
2s |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно, транспортные расходы минимальны, если груз перевозят на автотранспорте до пункта М, расположенного на расстоянии 14 s
 2 от пункта В.
2 от пункта В.
4. ПРИМЕНЕНИЕ ПОНЯТИЯ ПРОИЗВОДНОЙ В ЭКОНОМИКЕ. ЭЛАСТИЧНОСТЬ ФУНКЦИИ
Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции.
Эластичностью функции Ex ( y) называется предел отношения относительного приращения функции у к относительному приращению
переменной х при x |
0: |
|
|
|
|
|
|
|
|
|
|
|
Ex ( y) |
lim |
y |
: |
x |
|
x |
lim |
y |
|
x |
y . |
(4.1) |
y |
x |
|
y |
x |
|
y |
||||||
|
x 0 |
|
|
x 0 |
|
|
|
Эластичность функции показывает приближенно, на сколько процентов изменится функция y f (x) при изменении независимой переменной х на
1%.
Эластичность функции применяется при анализе спроса и потребления. Если эластичность спроса (по абсолютной величине) Ex ( y) 1, то спрос

|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
||
считают эластичным, |
|
если |
|
Ex ( y) |
|
1 - нейтральным, если |
|
Ex ( y) |
|
1 - |
|||||||||||
|
|
|
|
|
|||||||||||||||||
неэластичным относительно цены (или дохода). |
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 1. Рассчитать эластичность функции |
y |
x 2 |
|
3x |
|
1 и найти |
|||||||||||||||
значение показателя эластичности для х = 3. |
|
|
|
|
|
|
|
|
|
||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По формуле (4.1) эластичность функции |
|
|
|
|
|
|
|
|
|
||||||||||||
Ex ( y) |
|
x |
|
y |
|
|
|
x |
2x 3 |
x 2x |
3 |
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x 2 |
3x 1 |
x 2 |
|
|
|
|
|
|
|
|||||||
|
|
y |
|
|
3x 1 |
|
|
|
|
||||||||||||
Пусть х = 3, тогда Ex 3 ( y) 1,42 . Это означает, что если независимая
переменная возрастает на 1%, то значение зависимой переменной увеличится на 1,42%.
Пример 2. Пусть функция спроса у относительно цены х имеет вид y a  e 2x , где а – постоянный коэффициент. Найти значение показателя
e 2x , где а – постоянный коэффициент. Найти значение показателя
эластичности функции спроса при цене х = 3 ден.ед. Решение.
Рассчитаем эластичность функции спроса по формуле (4.1)
Ex ( y) |
x |
y |
x |
|
2a e |
2x |
2x . |
|
|
|
|
|
|||||
y |
a e |
|
2x |
|
||||
|
|
|
|
|
|
|||
Полагая х = 3 ден.ед., получим Ex |
3 ( y) 6 . Это означает, что при цене |
|||||||
х = 3 ден.ед. повышение цены на 1% вызовет снижение спроса на 6%, т.е. спрос эластичен.
Пример |
3. Функция спроса относительно дохода имеет вид |
s 4 1,2r |
0,44r 2 . Как изменится спрос, если доход увеличивается от |
100 у.е. до 150 у.е.?
Решение. Найдем эластичность спроса относительно дохода по
формуле |
|
|
|
|
|
Er (s) |
r |
s |
r |
|
(0,88r 1,2) . |
|
4 1,2r |
0,44r 2 |
|||
|
s |
|
|||
Oпределим значение эластичности, если доход равен r = 100 у.е.
E100 (s) 1,972%.
Так как доход увеличился на |
150 |
1 100% 50% |
, то, очевидно, спрос |
||
|
|
||||
100 |
|||||
|
|
|
|||
увеличится на 50 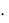 1,972% 98,6% .
1,972% 98,6% .
18
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ. ПРАВИЛА ИХ ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ
При выполнении индивидуального задания надо придерживаться указанных ниже правил.
1.Индивидуальное задание выполнять в тетради, оставляя поля для замечаний рецензента.
2.На обложке тетради должны быть написаны фамилия студента, его инициалы, название дисциплины и номер варианта.
3.В работу должны быть включены все задачи, указанные в задании. Индивидуальное задание, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
4.Решение задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номер задачи.
5.Перед решением каждой задачи надо выписать полностью её условие. Если несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
6.После получения отрецензированной работы студент должен исправить в ней все отмеченные рецензентом ошибки и недочеты. В связи с этим следует оставить в конце тетради чистые листы для работы над ошибками. Вносить исправления в текст работы ее рецензирования запрещается.
7.В случае незачета выполнить работу над ошибками, и сдать на повторную проверку.
Вариант индивидуального задания студент выбирает в соответствии со своим порядковым номером в журнале преподавателя.
19
Варианты индивидуальных заданий
Номер |
|
Номера задач контрольного задания |
|
|||
варианта |
|
|
|
|
|
|
1 |
1 |
|
31 |
61 |
|
91 |
2 |
2 |
|
32 |
62 |
|
92 |
3 |
3 |
|
33 |
63 |
|
93 |
4 |
4 |
|
34 |
64 |
|
94 |
5 |
5 |
|
35 |
65 |
|
95 |
6 |
6 |
|
36 |
66 |
|
96 |
7 |
7 |
|
37 |
67 |
|
97 |
8 |
8 |
|
38 |
68 |
|
98 |
9 |
9 |
|
39 |
69 |
|
99 |
10 |
10 |
|
40 |
70 |
|
100 |
11 |
11 |
|
41 |
71 |
|
101 |
12 |
12 |
|
42 |
72 |
|
102 |
13 |
13 |
|
43 |
73 |
|
103 |
14 |
14 |
|
44 |
74 |
|
104 |
15 |
15 |
|
45 |
75 |
|
105 |
16 |
16 |
|
46 |
76 |
|
106 |
17 |
17 |
|
47 |
77 |
|
107 |
18 |
18 |
|
48 |
78 |
|
108 |
19 |
19 |
|
49 |
79 |
|
109 |
20 |
20 |
|
50 |
80 |
|
110 |
21 |
21 |
|
51 |
81 |
|
111 |
22 |
22 |
|
52 |
82 |
|
112 |
23 |
23 |
|
53 |
83 |
|
113 |
24 |
24 |
|
54 |
84 |
|
114 |
25 |
25 |
|
55 |
85 |
|
115 |
26 |
26 |
|
56 |
86 |
|
116 |
27 |
27 |
|
57 |
87 |
|
117 |
28 |
28 |
|
58 |
88 |
|
118 |
29 |
29 |
|
59 |
89 |
|
119 |
30 |
30 |
|
60 |
90 |
|
120 |

20
ЗАДАЧИ
1-30. Исследовать функцию и построить её график.
1. |
a) y |
|
x 2 |
|
5 |
3 |
|
. |
|
|
|
|
|
|||
125 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
a) y 32x 2 x 2 |
1 3 . |
|
|
||||||||||||
3. |
a) y x 1 2 x 2 4 . |
|
|
|||||||||||||
4. |
a) y |
3x |
|
x3 . |
|
|
|
|
|
|||||||
5. |
a) y |
1 x |
2 |
|
|
x |
4 |
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
a) y |
|
x 2e |
x2 . |
|
|
|
|
|
|||||||
7. |
a) y |
|
1 |
|
x |
3 |
|
|
1 |
x |
2 |
5 |
. |
|||
3 |
|
|
2 |
|
6 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
8. |
a) y |
e2x |
|
x2 . |
|
|
|
|
|
|||||||
9. |
a) y |
1 |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
10. a) y |
|
x3 |
3x 2 . |
|
|
|
||||||||||
11. a) y |
|
ln x 2 |
1 . |
|
|
|
|
|||||||||
b) y |
x5 |
|
|
8 |
|
. |
|
|
|
|
|||||
|
|
x 4 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b) y |
|
|
|
|
x3 |
|
|
|
. |
|
|
|
|
||
|
|
x |
3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|||||
b) y |
|
|
x |
|
1 2 |
|
. |
||||||||
|
|
x |
|
1 3 |
|
||||||||||
b) y |
|
|
a |
|
|
x 3 |
|
. |
|||||||
|
|
a |
|
|
2x |
||||||||||
b) y |
|
|
x |
|
|
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
x3 |
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
b) y |
x3 |
|
|
3x |
. |
||||||||||
|
x 2 |
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
b) y |
|
x3 |
|
|
1 |
. |
|
|
|
|
|||||
|
|
4x |
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b) y |
x 2 |
|
|
5 |
|
. |
|
|
|
|
|||||
|
x |
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
b) y |
|
1 |
|
4x 2 . |
|||||||||||
|
|
|
|
||||||||||||
|
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
e x b) y x .
b) y x2 1 . x2
