Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4747

.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

729.62 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования «Хабаровская государственная академия экономики и права»

Кафедра математики и математических методов в экономике

Е.А. Мясников

ПРАКТИКУМ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ

Часть 1

Хабаровск 2012

УДК 51 (075.8)

ББК 11

М 99

Мясников Е. А. Практикум по математическому анализу. Часть 1 : учеб. пособие / Е. А. Мясников. – Хабаровск : РИЦ ХГАЭП, 2012. – 100 с.

Содержание пособия соответствует государственным образовательным стандартам дисциплин «Математика» и «Математический анализ» для бакалаврантов 1-го курса обучения. Предназначено для самостоятельных и аудиторных практических занятий. Включает общие схемы решения задач, образцы решения примеров разной сложности, задания для самостоятельной работы.

Составлено для бакалаврантов экономических вузов всех направлений подготовки, будет полезно студентам, обучающимся заочно, и всем, кто желает изучить или повторить курс математики самостоятельно.

Рецензенты:

А.Г. Зарубин, д-р физ.-мат. наук, профессор, зав. каф. прикладной математики и информатики ТОГУ;

В.Я. Прудников, канд. физ.-мат. наук, доцент каф. прикладной математики ДВГУПС.

Утверждено издательско-библиотечным советом академии

вкачестве учебного пособия

©Мясников Е.А., 2012

©Хабаровская государственная академия экономики и права, 2012

Предисловие

Цель пособия – помочь студентам 1-го курса освоить решение стандартных задач математического анализа.

Знание теории без практического применения в математике ценится невысоко, и серьёзное изучение её невозможно без систематической самостоятельной работы, основная часть которой – решение задач.

Сборники заданий по математике в основном создавались, когда преподаватель, составив вначале простейшие примеры, сам показывал решение, разбирал трудные вопросы и давал указания к домашней работе. Это было возможно при достаточном объёме аудиторных часов.

Теперь же, когда почти вся практическая работа выполняется студентами самостоятельно, особенности составления сборников приводят к тому, что студенты часто не знают, с чего начать работу – методы решения соседних задач могут существенно отличаться. По той же причине решение очередной задачи не помогает в выполнении следующей и потому быстро забывается. Кроме того, уровень первых же заданий нередко слишком высок, и студент переходит к более понятным дисциплинам.

Цель большинства задачников – научить студентов думать, однако такое умение (и не только в математике) предполагает знание простейших закономерностей и правил. Решение интересных и нестандартных задач невозможно без способности разбираться с простыми вопросами, доведённой до автоматизма.

В этом случае освоение сложной задачи сводится не к случайному поиску путей решения, а разбивается на последовательность стандартных действий, ни одно из которых не вызовет трудностей – пусть даже сам порядок действий окажется весьма необычен.

Пособие составлено по принципу постепенного усложнения. Изучение темы начинается с простых примеров, затем они усложняются, но в чём именно – обычно очевидно, чтобы разбираться именно с возникшей трудностью, а не начинать заново думать, на какую тему задача.

Каждый параграф имеет двухбуквенный код. Задачи, собранные под значком типа ИЧ1 или ОИ2, относятся к очередному вопросу темы. Если вопрос достаточно прост, под буквами перебираются возможные ситуации. Важные частные случаи нумеруются цифрами.

Задания даны «с запасом», и метод решения может стать вполне понятным до конца очередной группы примеров.

Образцы решения обычно даны перед заданием, если схема мало зависит от конкретного примера, и после задания – если надо показать отличия в методах.

Ответы, как правило, предложены там, где проверка требует большого времени, а сам ответ достаточно краток. Если же правильность решения или ошибка видны сразу (как при дифференцировании функций), проще обратиться к преподавателю или сверить ответы с группой.

Некоторые темы всё же не исчерпываются готовой схемой и предполагают предварительную работу на занятиях, с немедленным выяснением непонятных мест – например, построение графиков. Для них образцы решения не даны.

Там, где в изложении возникало противоречие между краткостью и строго-

стью	оформления, выбор сделан в пользу	первого.	Например, записи вида
y 2	2 3 5 правильнее читать как y 2 2	3 y 2	5 . Пособие не учебник,

преследует более скромные цели, и решение задач желательно совместить с изучением теории. В этом помогут разработки, выпущенные на кафедре МММЭ, доступные учебники, лекции собственного или любого другого преподавателя.

Впособии не предлагаются варианты заданий для самостоятельных и контрольных работ. Преподаватель, ведущий занятия, составит их намного удачнее, зная уровень подготовки группы, программу и темы, на которые следует обратить особое внимание. Тем не менее всегда можно составить задание в виде списка номеров задач.

Основная задача пособия по отношению к преподавателю – дать возможность спокойно и последовательно изложить теоретические сведения и показать практическое применение математики в специальности, а не отвлекаться на многочисленные способы решения задач, подобранных под конкретную тему.

В1-й части учтены темы математического анализа, входящие в программу 1-го семестра для бакалаврантов экономических вузов. В зависимости от направления подготовки часть тем можно оставить на факультативное изучение. Не включены темы «Применение производной в задачах оптимизации» и «Условный экстремум функции двух переменных», изложенные в [8].

Автор желает студентам успехов в изучении математического анализа и заранее благодарен за любые вопросы, замечания и сообщения о недостатках пособия. Высказать их можно по адресу: ХГАЭП, ауд. 511, кафедра МММЭ.

I.ЗАДАЧИ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ

§1. Линейная функция. Уравнение прямой. Парабола

Линейная функция	y	kx	b	называется также линейной зависимостью	или
линейной регрессией. Уравнение				y kx b подчёркивает, что y зависит от x,	а не
наоборот. Уравнение	Ax	By	C	0 , напротив, указывает на равноправие пере-

менных и применяется, когда линейная комбинация образует новую величину, например, производственные затраты.

Любая линия (не только прямая) пересекает ось абсцисс (ось OX), когда y 0 , а ось ординат (ось OY) – если x 0 . Поэтому для поиска точек пересечения линии с системой координат подставляем эти значения по очереди в уравнение линии, находим другую координату и тем самым – точку пересечения.

С точки зрения математического анализа запись y x

kx b точнее. Приня-

тая форма записи y

b связана с традициями аналитической геометрии.

ЛФ1. Отметьте точки в декартовой системе координат:

A 1; 0 ,

B 2; 0 , C

1; 0 ,

D 2; 0 ,

E 0,5; 0 ,

F 2,5; 0 ,

M 1 3; 0 ,

4 3; 0 ;

A 0;1 ,

B 0; 3 , C 0;

1 ,

D 0;

2 ,

E 0; 0,5 ,

F 0;1,5 ,

M 0;1 3 ,

N 0;

2 3 ;

A 1;1 , B 1; 1 , C 1;1 , D 1; 1 , E 2; 2 , F 2; 2 , M 2; 2 , N 2; 2 ;

A 2; 3 , B 3; 2 , C 2; 3 , D 3; 2 , E 2; 3 , F 2; 3 , M 3; 2 , N 3; 2 .

ЛФ2. Постройте прямые, параллельные осям координат:

а)

б)

в)

2 ;

г)

д)

1 3 ;

е)

0,5 ;

а)

б)

в)

2 ;

г)

д)

1 3 ;

е)

0,5 .

Как выглядят прямые x

0 и y

0 ?

ЛФ3. Постройте прямые, определив точки пересечения с осями координат:

а) x y 1;

б) x y 1;

в) x y

г) x y

1 ;

а) x y 2 ;

б) x y 2 ;

в) x y

2 ;

г) x y

2 ;

а) 2x y 4 ;

б) 2x y 4 ;

в) 2x y

г) 2x y

4 ;

а) x 2y 4 ;

б) x 2y 4 ;

в) x 2 y

г) x 2 y

4 ;

а) 2x 3y 6 ;

б) 2x 3y 6 ;

в) 2x 3y

6 ;

г) 3y 2x 6 ;

а) 3x 4y 24 ;

б) 4x 3y 24 ;

в) 3x 4 y 24 ;

г) 4x 3y 24 .

Пример 1. Построим прямую x

5 .

Если x

0 , то 0 y

откуда

5 и соответственно

5 . Значит, пря-

мая пересекает ось OY (на которой x

0 ) в точке y

5 .

Если же

0 , то x

5 ,

откуда x

5 . Поэтому прямая пересекает ось OX

(на которой y

0 ) в точке x

5 .

Отмечаем на оси OX точку

5 , на оси OY точку

5 и проводим пря-

мую, проходящую через эти точки.

Пример 2. Построим прямую 3x

7 y

42:

а) если x

0 , то 3 0

42, откуда 7y

42 и y

6 ;

б) если y

0 , то 3x

7 0

42 , откуда 3x

42 и x

14 .

Отмечаем на оси OX точку x

14 ,

на оси OY точку y

6 , и проводим прямую,

проходящую через точки.

ЛФ4. Постройте прямые, заданные уравнением с угловым коэффициентом:

1) а) y x ;

б) y

x ;

в) y x 1;

г) y x 1;

д) y 1 x ;

2) а) y 2x ;

б) y

2x ;

в) y 2x 1;

г) y 2x 1;

д) y 1 2x ;

3) а) y 3x ;

б) y

3x ;

в) y 3x 4;

г) y 3x 4 ;

д) y 4 3x ;

4) а) y

;

б) y

;

в) y

г) y

д) y 1

Пример 3. Построим прямую y

5 :

а) пусть x

0 , тогда y

2 0

5 . Отмечаем точку A 0; 5 ;

б) пусть x

2 , тогда y

5 1. Отмечаем точку B

2; 1 .

Прямая проходит через А и В (и продолжается в обе стороны).

Замечание. При слишком близких значениях x прямая получится неточно. Не следует также брать x, при которых получается большое (по модулю) значение y.

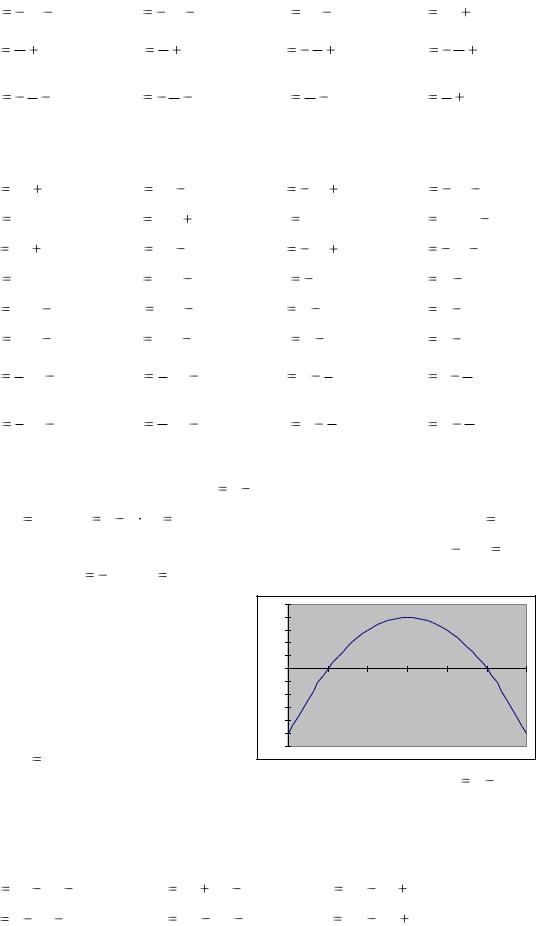
ЛФ5. Постройте прямые, обращая внимание на зависимость расположения прямой от знака и величины коэффициентов:

а) y 2x 3;

б) y 2x 3;

в) y 3

2x ;

г) y

2x 3;

д) y 3x 2 ;

3x 2 ;

ж) y 2 3x ;

з) y

3x 2 ;

а)

3x 4 ;

б) y 3x 4 ;

в)

3x ;

г) y

4 ;

д) y 4x 3;

3 ;

ж) y 3 4x ;

з)

4x 3;

а)

2x 1 ;

б) y 3x

в)

3x 1;

г)

2 ;

д) y

3x 1;

e) y

3x 2 ;

ж) y 3x 2 ;

з) y 3x 2;

4) а) y

б) y

в) y

1 ;

г) y

;

д) y

e) y

2 ;

ж) y

2 ;

з)

2 .

ЛФ6. Постройте параболы любым способом:

1) а) y x2

2 ;

б) y x2

2 ;

в) y

2 ;

г) y

x 2

2 ;

д) y

2x 2 ;

2x2

1 ;

ж) y

0,5x2 ;

з)

0,5x 2

2 ;

2) а) y x2

3 ;

б) y x2

3 ;

в) y

x 2

3 ;

г) y

3 ;

д) y

3x2 ;

3x2

2 ;

ж) y

0,5x2 ;

з)

0,5x2 ;

3) а) y 2x 2

4 ;

б) y 3x2

4 ;

в) y 4 2x 2 ;

г) y 4 3x2 ;

д) y 2x2

6 ;

e) y 3x2

6 ;

ж) y 6 2x 2 ;

з) y 6 3x2 ;

4) а) y

1 x2

2 ;

б) y

1 x2

в) y 2

1 x2 ;

г) y 1

1 x2

;

д) y

1 x2

3 ;

e) y

1 x2

2 ;

ж) y 3

1 x2

;

з) y 2

1 x2 .

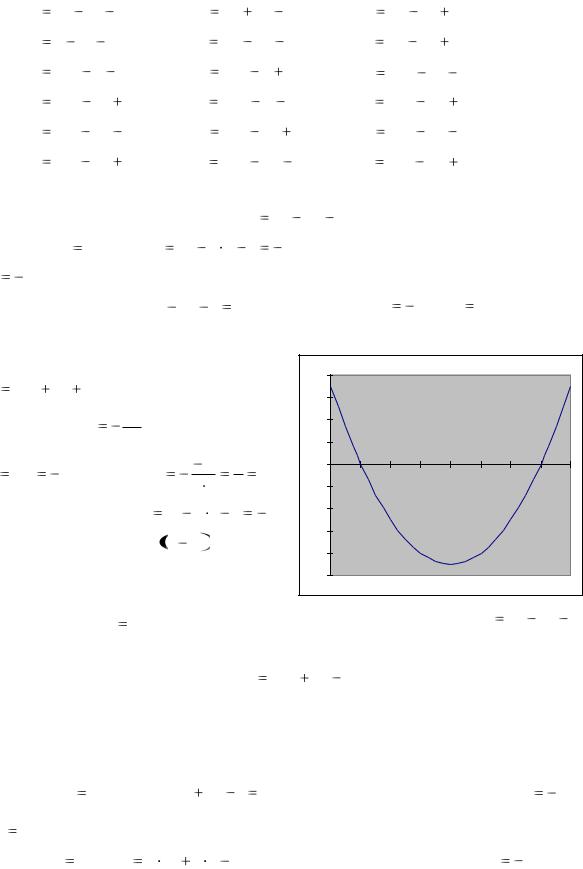
Пример 4. Построим параболу y

2x2 .

Если x

0 , то y

2 02

8 . Парабола пересекает ось OY в точке y

8 .

Чтобы найти точки пересечения с осью OX, решаем уравнение 8

2x2

0 ,

получаем точки x1

2 и x2

2 .

Перед квадратом стоит знак «–».

Значит, ветви направлены вниз.

В уравнении отсутствует линейное

слагаемое px,

поэтому вершина нахо-

-2 -3

-2

-1

-4

дится на оси OY. Общий вид параболы

-6

-8

дан на рисунке 1. Ось OY проходит че-

-10

-12

рез точку x

0 .

Рисунок 1 – Парабола y

2x2

ЛФ7. Постройте параболы, указав вершину и точки пересечения с осями ко-

ординат (если такие точки есть):

1) а) y x2

2x 8 ;

б) y x2

2x 8 ;

в) y 2x x2

8 ;

г) y 8 x2

2x;

д) x y 2

2 y 8 ;

е) x 2 y y 2

8 ;

2) а) y x2

3x 4 ;

б) y x 2

3x 4 ;

в) y 3x x 2

4 ;

г) y 4 x2

3x;

д) x y 2

3y 4 ;

е) x 3y y 2

4 ;

3) а) y 2x2

x 3 ;

б) y 2x2

x 3 ;

в) y 2x2

5x 3;

г) y 2x2

5x 3;

д) x 2 y 2

y 3 ;

е) x 2 y 2

5y 3 ;

4) а) y 3x2

2x 1;

б) y 3x2

2x 1;

в) y 3x2

4x 1 ;

г) y 3x2

4x 1;

д) x 3y 2

2 y 1;

е) x 3y 2

4 y 1.

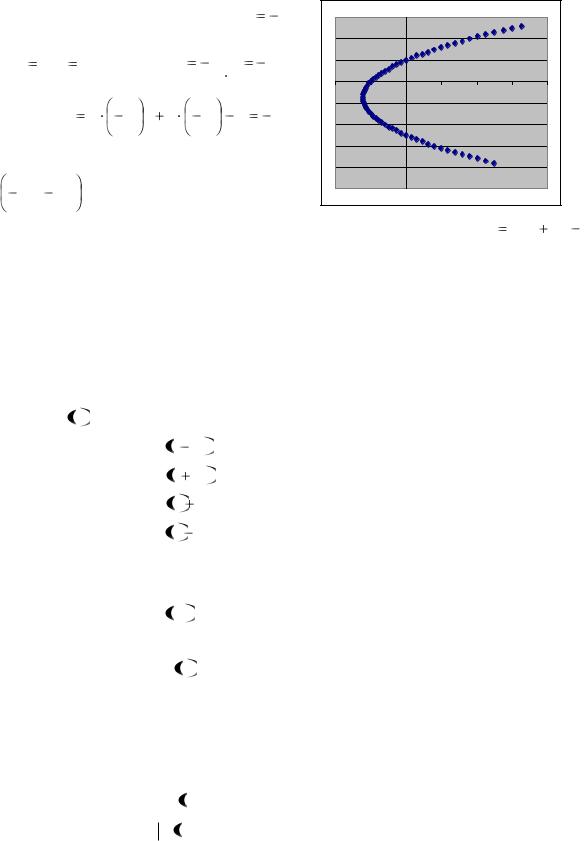
Пример 5. Построим параболу y

x 2

2x 8 .

Пусть x

0 , тогда y

8 . Парабола пересекает ось OY в точке

Решим уравнение x2

0. Получим точки x

2 и x

4 . В них пара-

бола пересекает ось OX.

Когда парабола задана уравнением

ax2

c , её вершина находится

по формуле

. В нашем случае

1, b

2 , поэтому x0

2 1 2

-2 -3

-2

-1

Соответственно,

2 1

9 ,

-4

и вершина – в точке M 1;

9 .

-6

-8

Ветви идут вверх – перед квадратом

-10

в уравнении стоит знак «+». Ось OY

проходит через x

0 (рисунок 2).

Рисунок 2 – Парабола y

x 2

Пример 6. Построим параболу x

2 y 2

5 .

Ветви направлены по горизонтали, поскольку x квадратично зависит от y.

При этом перед квадратом в уравнении стоит знак «+» и ветви идут в положи-

тельном направлении – вправо.

Пусть x	0 , тогда 2 y2	3y	5 0 . Решение уравнения – точки	y	5	и
Пусть x	0 , тогда 2 y2	3y	5 0 . Решение уравнения – точки	y		и
				1	2
					2
y2 1, в них парабола пересекает ось OY.
Если y	0 , то x 2 02	3 0	5 и парабола пересекает ось OX в x	5 .

	Вершину находим по формуле										y0				b

															2a
															2a
при a				2, b		3 , поэтому y0				3		3		.
при a				2, b		3 , поэтому y0			2		2	4		.
									2		2	4
При этом x0						2	3 2	3	3		5		49			.
При этом x0						2	4	3	4		5		8			.
							4		4				8
	Вершина параболы находится в точке
M		3	;		49	(рисунок 3).
M	4		;	8		(рисунок 3).
	4			8

		3
		2
		1
		0
-10	-5	-1 0	5	10	15	20
		-2
		-3
		-4
		-5
Рисунок 3 – Парабола x					2 y 2	3y	5

§ 2. Элементарные преобразования графиков

Пусть на некотором промежутке (интервале или отрезке) построен график функции f x . Тогда на основе этого графика:

1)	а) график функции	f	x	p получается сдвигом вправо на p единиц;
	б) график функции	f	x	p получается сдвигом влево на p единиц;
	в) график функции	f	x	P получается сдвигом вверх на P единиц;
	г) график функции	f	x	P получается сдвигом вниз на P единиц.
Эти преобразования называются сдвигом графика;
2)	а) график функции	f	kx	получается сжатием в k раз вдоль оси ОХ
	( в k раз приближается к оси OY);
	б) график функции Kf		x	получается растяжением в K раз вдоль оси OY

( в K раз отдаляется от оси ОХ).

Эти преобразования называются растяжением графика;

3) кроме того,

а) график функции 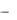f xполучается отражением от оси OX;

б) график функции f x получается отражением части, лежащей ниже оси ОХ, относительно этой оси. Затем график под осью ОХ удаляется. Часть, лежащая выше оси OX, не меняется.

Область определения функции (если таковой областью не служит вся числовая ось) меняется в случаях 1а, 1б и 2а; область значений – в остальных случаях.

ЭП1. Постройте график функции

x . При помощи элементарных преобра-

зований постройте графики функций

x .

x2 ;

а) f

x 1 2 ;

б) f

x 2 2 ;

в) f

г)

1 ;

д)

0,5x2 ;

е)

2x2 ;

ж)

x2 ;

з)

0,5x 2 ;

и)

2 x

1 2 ;

к)

2x2

1 ;

л)

x 2 2 ;

м)

0,5x2 ;

x ;

а) f1 x

x 2 ;

б) f2 x

x 2 ;

в) f3 x

x 2 ;

г) f4 x

1 ;

д) f5 x

x ;

е) f6 x

0,5

x ;

ж) f7 x

x ;

з) f8 x

2 x ;

и) f9 x

2 x 2 ;

к) f10 x

x 2 ;

л) f11 x

x 2 1 ;

м) f12 x

2 x 2 1;

cos x ;

а)

cos x

;

б)

cos x

;

в)

cos x

г) f4 x

cos x 1 ;

д) f5 x

2 cos x ;

е) f6 x

0,5cos x ;

ж)

cos x ;

з)

2 cos x ;

и)

2 cos x

;

к)

f10

cos x

;

л)

f11

2 cos x

м)

f12

2 cos x

1 ;

(правая ветвь);

а) f1 x

;

б) f2 x

;

в) f3 x

г) f4 x

д) f5 x

;

е) f6 x

;

ж) f7 x

;

з) f8 x

2 ;

и) f9 x

;

к) f10 x

;

л) f11 x

;

м) f12 x

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2022728.06 Кб24742.pdf
#
13.11.2022728.15 Кб54743.pdf
#
13.11.2022728.6 Кб34744.pdf
#
13.11.2022728.86 Кб14745.pdf
#
13.11.2022728.91 Кб34746.pdf
#
13.11.2022729.62 Кб04747.pdf
#
13.11.2022730.56 Кб14748.pdf
#
13.11.2022731.01 Кб24749.pdf
#
13.11.2022731.07 Кб14750.pdf
#
13.11.2022732.22 Кб14751.pdf
#
13.11.2022732.57 Кб24752.pdf