Аверянов САПР в електрофизике Ч.1 2011

дающих между собой чисел, каждое из которых можно записать в k

разрядную ячейку компьютера, равно 2k . Поэтому приходится вместо непрерывной совокупности случайных чисел с равномерным распределением в качестве исходной использовать дискрет-

ную совокупность 2k чисел с одинаковыми вероятностями появления любого из них.

Такое распределение иногда называют квазиравномерным, а генераторы, использующие физические способы генерирования, на-

зывают генераторами истинно случайных чисел. Однако следует отметить, что расхождения в параметрах распределений (равномерного и квазиравномерного) даже на 16-разрядной сетке сравнительно небольшое.

Если учесть, что оценить две основные характеристики равномерного распределения математического ожидания M и дисперсию σ можно, используя следующее соотношение [8]:

то можно получить табл. 3.1, в которой приводятся измерения значения дисперсии квазиравномерного распределения σζ в зависимости от разрядности сетки и относительная ошибка этого параметра (по отношению к точному значению σ).

Таким образом, уже на 15-ти разрядах ошибка в оценке дисперсии наблюдается в пятом знаке. Ошибка оценки математического ожидания и того меньше.

На первых вычислительных машинах в качестве генераторов истинно случайных чисел применялись специальные приставки, наиболее часто использующие либо радиоактивные источники, в которых за равные интервалы времени регистрировалось количество испускаемых частиц (четное z = 0 , нечетное z =1); либо шумы электронных ламп («белый» шум), в которых за равные промежутки времени регистрировались превышения колебаний напряжения

71

на аноде над номинальных значением и также четные превышения оценивались как z = 0 , а нечетные как z =1. В современных микропроцессорах «привязка» производится к внутренним процессам кристалла. Так, в процессорах x86 сообщалось, что уже у МП Pentium II появился генератор истинно случайных чисел. Основным недостатком генераторов истинно случайных чисел считается невозможность воспроизведения одинаковых последовательностей чисел, т.е. повторяемости одной и той же последовательности, что бывает очень важным свойством генератора в процессе проектирования. Второй способ получения случайных последовательностей связан с генерацией так называемых псевдослучайных чисел непосредственно на вычислительной машине с помощью специальных алгоритмов.

Первый алгоритм для получения псевдослучайных чисел был предложен Дж. Нейманом. Он назывался методом срединного квадрата. Алгоритм этого метода чрезвычайно прост. Берется четырехзначное число, возводится в квадрат, выбираются четыре цифры из середины возведенного числа и эта процедура повторяется многократно. В качестве случайных чисел используются полу-

ченные числа, умноженные на 10 −4 , т.е. получаются числа в интервале [0, 1]. Но этот алгоритм не оправдал себя, поскольку алгоритм выдавал неравномерно большее число малых значений в получаемой последовательности.

В настоящее время разработано большое количество генераторов псевдослучайных чисел. Практически во всех наиболее распространенных языках программирования наряду с библиотеками элементарных функций включаются генераторы псевдослучайных чисел.

Однако наряду с очевидными достоинствами этих генераторов – возможность многократного воспроизведения одних и тех же последовательностей чисел, простота алгоритмов и способа их реализации, основным и весьма серьезным недостатком такого способа получения случайных чисел является ограниченность «запаса» псевдослучайных чисел. Имеется в виду повторяемость или цикличность (периодичность) в последовательности случайных чисел, которая наступает значительно раньше, чем генераторы истинно случайных чисел заполняют разрядную сетку компьютера. Точные, аналитические методы оценки периодичности, как правило, отсутствуют, тем более что большинство генераторов используют эвристические ал-

72

горитмы. В связи с этим большое значение приобретают методы экспериментальной проверки качества этих алгоритмов. Хотя проверять качество генераторов истинно случайных чисел также целесообразно из-за возможных сбоев в аппаратуре. Этот вопрос будет рассмотрен в дальнейшем. Предварительно необходимо коснуться методов статистической обработки получаемых случайных последовательностей, которая предваряет проверку их качества.

3. Понятие статистического ряда и гистограммы [7]. Наибо-

лее полное представление о последовательности случайных чисел дают их плотности распределения. Описание статистических последовательностей представляется статистическим рядом, а графически в виде гистограммы.

Предположим, что в нашем распоряжении результаты генерации случайной величины X. Разделим весь диапазон наблюдаемых значений X на интервалы (или разряды) и подсчитаем количество значений mi , приходящее на каждый интервал (разряд). Это число

разделим на общее число генерируемых чисел n и найдем частоту (вероятность), соответствующуюу данному разряду:

Pi* = mni .

Сумма частот должна быть равна единице, а их последовательность представляетсяввидетабл. 3.2, называемойстатистическимрядом.

Если случайное число попадает на границу интервала, то можно добавлять в каждый интервал по 1/2.

Число разрядов, из которых следует группировать статистический ряд, не должно быть слишком большим (при этом проявляются незакономерные колебания), при слишком малом числе разрядов распределения оцениваются слишком грубо.

Практика показывает, что в большинстве случаев рационально выбирать число разрядов 10–20. Размер случайной последовательности (количество случайных чисел) следует подбирать таким образом, чтобы в каждый подынтервал попадало не менее десяти чисел.

73

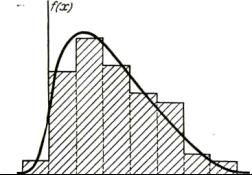
Статистический ряд оформляется графически в виде так называемой гистограммы (иногда в виде спектра или полигона) рис. 3.6. По оси абсцисс откладывают разряды, а по каждому из разрядов, как на основании строится прямоугольник, площадь которого равна частоте попадания случайной величины в данный разряд. Для построения гистограммы необходимо частоту каждого разряда разделить на его длину, а полученное число взять в качестве высоты прямоугольника. Из способа построения гистограммы следует, что полная площадь ее равна единицы.

Рис. 3.6. Гистограмма случайной величины распределений

Гистограмма является основным объектом оценки качества генераторов случайных (или псевдослучайных) последовательностей чисел, при использовании критериев согласия.

4. Критерии согласия [7]. Вопрос о качестве того или иного способа генерации случайных последовательностей равномерно распределенных чисел является одним из основных (если не основным) при проведении статистического моделирования.

Естественно, возникает вопрос: объясняются ли естественные расхождения между теоретическим распределением и полученной (статистической) гистограммой случайными обстоятельствами, связанными с ограниченным числом испытаний или они являются существенными и связаны с низким качеством способа генерации? Для ответа на этот вопрос служат так называемые «критерии согласия». Идея применения критериев согласия заключается в следующем.

74

На основании данного статистического материала нам предстоит проверить гипотезу H, состоящую в том, что случайная величина X подчиняется некоторому определенному закону распределения. Этот закон может быть задан в той или иной форме: например, в виде функции распределения F(x) или в виде плотности распределения

f (x) , или же в виде совокупности вероятностей pi , где pi – веро-

ятность того, что величина X попадет в пределы i-го разряда.

Так как из этих форм функция распределения F(х) является наиболее общей и определяет собой любую другую, будем формулировать гипотезу Н, как состоящую в том, что величина X имеет функцию распределения F(х).

Для того чтобы принять или опровергнуть гипотезу H, рассмотрим некоторую величину U, характеризующую степень расхождения теоретического и статистического распределений. Величина U может быть выбрана различными способами; например, в качестве U можно взять сумму квадратов отклонений теоретических вероят-

ностей Pi от соответствующих частот р*i или же сумму тех же

квадратов с некоторыми коэффициентами («весами»), или же максимальное отклонение статистической функции распределения F*(x) от теоретической F(x) и т.д. Допустим, что величина U выбрана тем или иным способом. Очевидно, это есть некоторая случайная величина. Закон распределения этой случайной величины зависит от закона распределения случайной величины X, над которой производились опыты, и от числа опытов п. Если гипотеза Н верна, то закон распределения величины U определяется законом распределения величины X (функцией F(x)) и числом п.

Допустим, что этот закон распределения нам известен. В результате данной серии опытов обнаружено, что выбранная нами мера расхождения U приняла некоторое значение и. Спрашивается, можно ли объяснить это случайными причинами или же это расхождение слишком велико и указывает на наличие существенной разницы между теоретическим и статистическим распределениями и, следовательно, на непригодность гипотезы H? Для ответа на этот вопрос предположим, что гипотеза Н верна, и вычислим в этом предположении вероятность того, что за счет случайных причин, связанных с недостаточным объемом опытного материала, мера

75

расхождения U окажется не меньше, чем наблюденное нами в опыте значение и, т.е. вычислим вероятность события: U ≥ u.

Если эта вероятность весьма мала, то гипотезу Н следует отвергнуть как малоправдоподобную; если же эта вероятность значительна, следует признать, что экспериментальные данные не противоречат гипотезе Н.

Возникает вопрос о том, каким же способом следует выбирать меру расхождения U. Оказывается, что при некоторых способах ее выбора закон распределения величины U обладает весьма простыми свойствами и при достаточно большом п практически не зависит от функции F(x). Именно такими мерами расхождения и пользуются в математической статистике в качестве критериев согласия.

Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый «критерий χ2» Пирсона.

Предположим, что произведено п независимых опытов, в каждом из которых случайная величина X приняла определенное значение. Результаты опытов сведены в k разрядов и оформлены в виде статистического ряда, о котором говорилось ранее (табл. 3.3).

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина X имеет данный закон распределения (заданный функцией распределения F(х) или плотностью f(х), см. рис. 3.6). Назовем этот закон распределения

теоретическим.

Зная теоретический закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов:

p1, p1, p1, ..., pk .

Проверяя согласованность теоретического и статистического распределений, будем исходить из расхождений между теоретиче-

скими вероятностями pi и наблюденными частотами p *i . Естест-

76

венно выбрать в качестве меры расхождения между теоретическим и статистическим распределениями сумму квадратов отклонений (pi*, …, pi), взятых с некоторыми «весами» сi:

k 2

U = ∑ci (pi* − pi ) .

i=1

Коэффициенты ci («веса» разрядов) вводятся потому, что в общем

случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Действительно, одно и то

же по абсолютной величине отклонение p* − pi может быть малозначительным, если сама вероятность pi велика, и очень заметным, если она мала. Поэтому естественно «веса» взять обратно пропорциональными вероятностям разрядов pi . Далее возникает

вопрос о том, как выбрать коэффициент пропорциональности. К. Пирсон показал, что если положить

ci = n , pi

то при больших n закон распределения величины U обладает весьма простыми свойствами: он практически не зависит от функции распределения F(x) и от числа опытов п, а зависит только от числа разрядов k, а именно: этот закон при увеличении п приближается к так называемому распределению* χ2.

* Распределением χ2 с r степенями свободы называется распределение суммы квадратов r независимых случайных величин, каждая из которых подчинена нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Это распределение характеризуется плотностью

∞

где Γ(α) = ∫tα−1e−t dt – неизвестная гамма-функция.

0

77

При таком выборе коэффициентов ci мера расхождения обычно обозначается χ2:

χ2 = n∑k ( pi* − pi )2 .

i=1 pi

Для удобства вычислений (чтобы не иметь дело с дробными величинами с большим числом нулей) можно ввести п под знак суммы

и, учитывая, что pi* = mni , где mi – число значений в i-м разряде,

привести предыдущую формулу к виду

U= χ2 = ∑k (mi −npi )2 .

i=1 npi

Распределение χ2 зависит от параметра r, называемого числом «степеней свободы» r, которое равно числу разрядов k минус число независимых условий («связей»), наложенных на частоты pi* .

Примерами таких условий могут 6ыть

k

∑pi* =1,

i=1

если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);

k

∑xi pi* = mx .

i=1

Если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое и статическое средние значения;

k

∑(xi −m*x )2 pi* = Dx ,

i=1

если требуем, кроме того, совпадения теоретической и статистической дисперсий и т.д.

Для распределения χ2 составлены специальные таблицы. Пользуясь этими таблицами, можно для каждого значения χ2 и числа степеней свободы r найти вероятность р того, что величина, распределенная по закону χ2, превзойдет это значение. В табл. 3.4 входами являются значение вероятности р и чисел степеней свободы r.

78

Числа, стоящие в таблице, представляют собой соответствующие значения χ2.

Распределение χ2 дает возможность оценить степень согласованности теоретического и статистического распределений. Будем исходить из того, что величина X действительно распределена по закону F(x). Тогда вероятность р, определенная по таблице, есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений будет не меньше, чем фактически наблюденное в данной серии опытов значение χ2. Если эта вероятность р весьма мала (настолько мала, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе H о том, что закон распределения величины X есть F(x). Эту гипотезу следует отбросить как неправдоподобную. Напротив, если вероятность р сравнительно велика, можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счет случайных причин. Гипотезу H о том, что величина X распределена по закону F(x), можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.

Таким образом, схема применения критерия χ2 к оценке согласованности теоретического и статистического распределений сводится к следующему:

1)определяется мера расхождения χ2 по формуле, приведенной ранее;

2)определяется число степеней свободы r как число разрядов k минус число наложенных связей s:

r = k − s ;

79

3) по r и χ2 с помощью табл. 3.5 определяется вероятность того, что величина, имеющая распределение χ2 с r степенями свободы, превзойдет данное значение χ2 (если эта вероятность весьма мала, гипотеза отбрасывается как неправдоподобная; если эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным).

Насколько мала должна быть вероятность р для того, чтобы отбросить или пересмотреть гипотезу, – вопрос неопределенный; он не может быть решен из математических соображений, так же как и вопрос о том, насколько мала должна быть вероятность события для того, чтобы считать его практически невозможным. На практике, если р оказывается меньшим чем 0,1, рекомендуется проверить эксперимент, если возможно – повторить его и в случае, если заметные расхождения снова появятся, пытаться искать более подходящий для описания статистических данных закон распределения.

Следует особо отметить, что с помощью критерия χ2 (или любого другого критерия согласия) можно только в некоторых случаях опровергнуть выбранную гипотезу H и отбросить ее как явно несогласную с опытными данными; если же вероятность р велика, то этот факт сам по себе ни в коем случае не может считаться доказательством справедливости гипотезы Н, а указывает только на то, что гипотеза не противоречит опытным данным.

С первого взгляда может показаться, что чем больше вероятность р, тем лучше согласованность теоретического и статистического распределений и тем более обоснованным следует считать выбор функции F(x) в качестве закона распределения случайной

величины. В действительности это не так. Допустим, например, что, оценивая согласие теоретического и статистического распре-

делений по критерию χ2, получили p = 0,99. Это значит, что с вероятностью 0,99 за счет чисто случайных причин при данном числе опытов должны были получиться расхождения большие, чем наблюденные. Мы же получили относительно весьма малые расхождения, которые слишком малы для того, чтобы признать их правдоподобными. Разумнее признать, что столь близкое совпадение теоретического и статистического распределений не является случайным и может быть объяснено определенными причинами, связанными с регистрацией и обработкой опытных данных (в частности, с весьма распространенной на практике «подчисткой» опыт-

80