2.4. Энтальпия

В XIX столетии американский физик Гиббс ввел в термодинамику сложную функцию вида

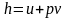, , (2.31)

которая была названа удельной энтальпией.

Энтальпия является функцией состояния, её величина определяется состоянием тела, поэтому изменение энтальпии h определяется только начальным и конечным состояниями тела. Таким образом, энтальпия  это параметр состояния, а её дифференциал является полным дифференциалом. Энтальпия произвольного количества вещества массой m: 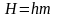, Дж.

Из выражения (2.31) следует .

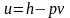Подставив это выражение в уравнение первого закона термодинамики (2.5), получим , ,

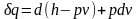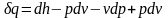. (2.32)

Формула (2.32) − еще одно аналитическое выражение первого закона термодинамики.

При p =const vdp = 0,  q_p = dh. В то же время q_p = c_pdT

 см. уравнение (2.32). Следовательно, .

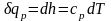Проинтегрировав выражение c_pdT = dh

от 0 до t и условно приняв, что при нормальных условиях (t = 0^оС, p = 760 мм рт. ст.), h_о = 0, получим

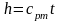. (2.33)

Удельная энтальпия численно равна количеству теплоты, которую нужно подвести к 1 кг вещества для нагревания его от нуля до заданной температуры при постоянном давлении. Из выражения q_p = dh = c_pdt

после интегрирования получим 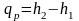, (2.34)

или 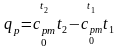. (2.35)

Следовательно, 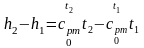. (2.36)

Формулой (2.34) удобно пользоваться в теплотехнических расчётах, так как значения энтальпии, как и теплоемкостей, даны в таблицах термодинамических свойств веществ.

2.5. Энтропия идеального газа

Кроме удельной внутренней энергии и энтальпии в термодинамике существует еще одна функция состояния, которая называется удельной энтропией. Ее обозначают символом s, единица измерения  . Энтропия произвольного количества вещества массой m:  S = sm, Дж/К. (2.37)

Дифференциал удельной энтропии является полным дифференциалом и определяется из выражения

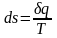, (2.38)

где q  функция процесса: q – неполный дифференциал. Умножив q на интегрирующий множитель 1/Т, получим полный дифференциал ds. Из формулы (2.38) следует 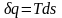(2.39)

или 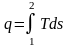^. (2.40)

Сравнивая формулу (2.39) с аналитическим выражением работы изменения объема l = p·dv

– см. уравнение (2.1), видим, что для передачи энергии в форме деформационной работы нужна разность давлений, для передачи энергии в форме теплоты нужна разность температур, что деформационная работа совершается только при изменении удельного объема, теплота подводится (отводится) только при изменении энтропии. Можно также сказать, что энтропия в равновесных процессах изменяется только в результате подвода (отвода) теплоты.

Следовательно, энтропия – физическая величина, изменение которой является признаком обмена энергией в форме теплоты в равновесных процессах.

Значение энтропии для заданного состояния определяется интегрированием выражения (2.38): 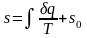, где s_o – константа интегрирования, которая не может быть определена с помощью первого и второго законов термодинамики.

Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:

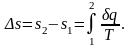
В любом процессе идеального газа du = c_vdT,

А q = Tds.

Подставим эти выражения в уравнение первого закона термодинамики (2.31):

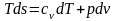
или 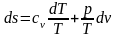. Из уравнения 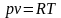следует, что .

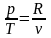Тогда .

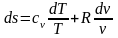После интегрирования получается: 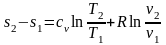. (2.41)

Чтобы выразить изменение энтропии через другие параметры состояния, запишем отношение уравнений Клапейрона для состояний 2 и 1:

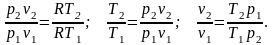
Подставив в уравнение (2.41) отношение 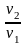, а затем 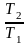, получим

;

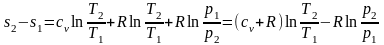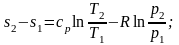(2.42)

;

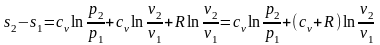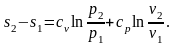(2.43)

Зависимости (2.41)–(2.43) показывают, что изменение энтропии идеального газа зависит от параметров начального и конечного состояний и не зависит от процесса. Поэтому 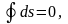то есть энтропия является параметром состояния, позволяющим исследовать процессы преобразования энергии.

Из выражения (2.39) следует:

- если ds > 0, то и q > 0 (теплота подводится);

- если ds < 0, то и q < 0 (теплота отводится).

Т

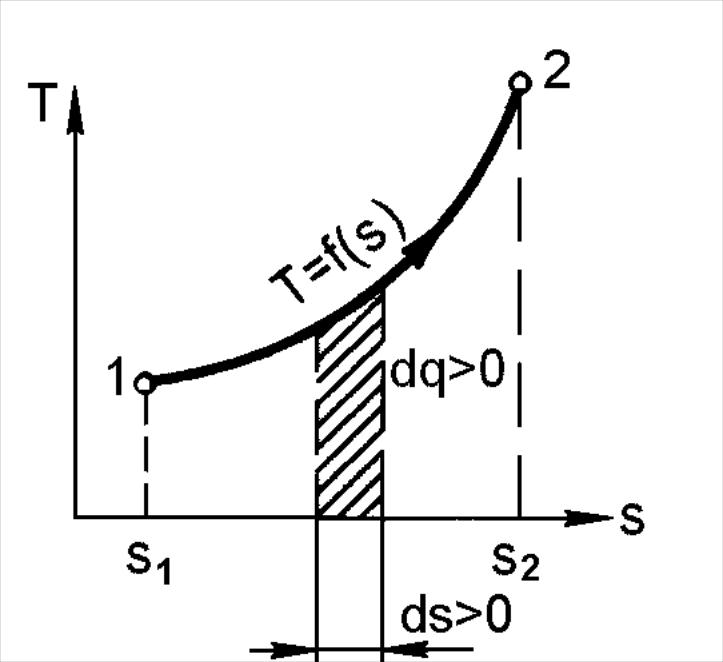
Рис. 2.8. Ts-диаграмма

идеального газа

аким образом, по изменению энтропии в обратимом процессе можно судить о направлении теплового потока между рабочим телом и окружающей средой. Ни один из ранее рассмотренных параметров состояния такой возможности не давал. Особенно важным является возможность использования энтропии при исследовании процессов с помощью диаграммы Ts.

В Ts-диаграмме так же, как и в pv-диаграмме, равновесное состояние термодинамической системы (рабочего тела) изображается точкой, а равновесный термодинамический процесс – линией (рис. 2.8).

В равновесном процессе q= Tds,

а 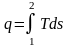– см. уравнения (2.38) и (2.40).

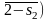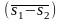Следовательно, площадь, ограниченная линией процесса , крайними ординатами и , отрезком оси абсцисс , описывается выражением

.

Поэтому Ts-диаграмма называется тепловой или энтропийной диаграммой.

Из изложенного видно, что теплота, как и работа, не является параметром состояния. Теплота, как уже отмечалось, является функцией процесса. Количество подведенной (отведенной) теплоты зависит от характера процесса, так как между заданными точками 1 и 2 можно провести разнообразные кривые (процессы), и площадь под этими процессами, а следовательно, и теплота q_1-2, будут иметь различные значения.

С помощью Ts-диаграммы можно определить не только теплоту, но и по характеру процесса на этой диаграмме  знак теплоты. Знаки элементарного количества теплоты и приращения энтропии совпадают. Следовательно, если ds > 0 (рис. 2.8), теплота подводится независимо от того, увеличивается или уменьшается температура.

Если же удельная энтропия уменьшается, то есть ds < 0, теплота отводится также, независимо от знака изменения температуры. Признаком подвода теплоты может служить только рост удельной энтропии, а признаком отвода – её уменьшение.