Лекция№2

Глава 2. Первый закон термодинамики

ДЛЯ ЗАКРЫТЫХ СИСТЕМ

2.1. Виды энергии

Первый закон термодинамики является частным случаем всеобщего закона сохранения и превращения энергии применительно к тепловым и механическим явлениям, протекающим в термодинамических системах и формулируемого как «Энергия не исчезает и не возникает вновь, она лишь переходит из одного вида в другой в различных физических, химических и других процессах».

Неотъемлемым свойством материи, является движение. Мерой движения является энергия. Тела при взаимодействии обмениваются количеством движения – энергией.

В термодинамике нас интересует преобразование тепловой энергии (теплоты) в механическую энергию (работу). Роберт Майер в 1842 году на основании опытов установил прямую пропорциональность между затраченной теплотой Q, Дж и полученной работой L, Дж

Q = L, Дж. (2.0)

Причём, в установленном соотношении Майера говорится не только об эквивалентности теплоты и работы, то есть о количественном постоянстве энергии, но и об изменении качества самой энергии, ведь происходят взаимопревращения различных форм движения.

Полная энергия газа Е состоит из внешней Е_внеш и внутренней U. Е= Е_внеш+ U

где Е_внеш – представляет собой энергию газа как единого целого и энергию газа в поле сил тяжести, Дж;

U – внутренняя энергия газа, Дж.

На практике удобнее пользоваться удельной внутренней энергией

.

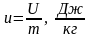Внутреннюю энергию можно представить в виде суммы

u_внутр=u_пост+u_вращ+u_колеб+u_взаим ,

где u_пост – энергия поступательного движения частиц (молекул);

u_вращ – энергия вращательного движения частиц (молекул);

u_колеб – энергия колебательного движения частиц (молекул);

u_взаим – энергия взаимодействия между молекулами (учитывается в реальных газах).

Сумма u_пост+u_вращ+u_колеб – представляет собой кинетическую составляющую внутренней энергии, а u_взаим – потенциальная составляющая внутренней энергии.

Поскольку кинетическая составляющая внутренней энергии определяется температурой газа, а потенциальная её составляющая при заданной температуре зависит ещё и от удельного объёма v или давления р (от v или р зависит расстояние между молекулами), то полная внутренняя энергия является функцией двух параметров. Такие величины являются термодинамическими параметрами состояния.

Кинетическая составляющая зависит от температуры, потенциальная – от давления. Следовательно:

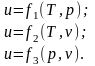
Внутренняя энергия идеального газа является функцией только температуры:

.

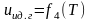Внутренняя энергия сложной системы равна сумме внутренних энергий отдельных её частей, то есть обладает свойствами аддитивности. Внутренняя энергия является функцией состояния, она определяется состоянием, в котором система находится в данный момент, ее изменение u в термодинамическом процессе не зависит от пути протекания процесса и определяется только начальным и конечным состоянием системы.

П

Рис. 2.1. Изменение

внутренней энергии

редположим, что тело из состояния 1 переходит в состояние 2 тремя различными термодинамическими процессами а, b, с (рис 2.1). При этом происходит изменение внутренней энергии на следующую величину:

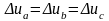
- в процессе а 

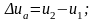
- в процессе b 

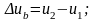
- в процессе с 

Таким образом, , или .

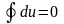Бесконечно малое изменение внутренней энергии du есть полный дифференциал внутренней энергии. Для идеального газа

,

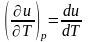так как u_ид.г. является функцией только температуры.

Энергия  это мера движения материи. При протекании термодинамических процессов тела, участвующие в этих процессах, обмениваются энергией. Передача энергии от одного тела к другому может происходить двумя способами.

Первый способ реализуется при непосредственном соприкосновении тел с различной температурой в результате обмена кинетической энергией между молекулами соприкасающихся тел, либо в результате переноса внутренней энергии тел путем электромагнитных волн (излучением). При этом энергия передается от более нагретого тела к менее нагретому.

Количество переданной энергии называется количеством теплоты, способ передачи энергии – передача в форме теплоты, или микрофизическая форма передачи энергии. Теплота обозначается символом Q. Единицей измерения является Дж и кратные величины. Удельное количество теплоты:

, .

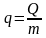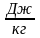Подведенную к телу теплоту принято считать положительной, отведенную от тела – отрицательной. Здесь и в дальнейшем при описании элементарного количества теплоты q вместо оператора d используется обозначение , так как элементарное количество теплоты не являются полным дифференциалом теплоты, в отличие от дифференциала внутренней энергии 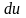, и его нельзя называть приращением теплоты.

Количество теплоты, участвующей в термодинамическом процессе, зависит от процесса перехода тела из начального состояния в конечное. Теплота передается только при наличии термодинамического процесса. Нет процесса  нет теплоты.

Второй способ передачи энергии связан с наличием силовых полей или внешнего давления. Передача энергии происходит либо при движении тела в силовом поле, либо в результате изменения объема под действием внешнего давления. В этом случае энергия передается в форме работы (макрофизическая форма передачи энергии). Количество переданной энергии в процессе называется работой.

Работа обозначается символом L, единица измерения работы − Дж и кратные величины. Удельная работа:

, .

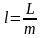При расширении газ (рабочее тело) совершает работу против внешних сил; при сжатии внешние силы совершают работу над газом (рабочим телом). Работу, совершаемую газом, принято считать положительной, работу, совершаемую над газом, – отрицательной.

Элементарное количество работы l, как и теплотыq, не является полным дифференциалом работы l, и его нельзя назвать приращением работы, поэтому вместо оператора d используется обозначение .

Допустим, в цилиндре с поршнем находится 1 кг рабочего тела (газа) под давлением р, площадь поршня  f. Газ, расширяясь, переходит из состояния 1 в состояние 2 (рис. 2.2). При этом поршень перемещается и совершается работа l.

При изменении объема на бесконечно малую величину dυ совершается элементарная работа δl, равная произведению действующей силы на путь её действия. Действующая сила – pf, путь действия – ds. Тогда 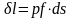, , 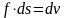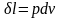. (2.1)

Формула (2.1) является аналитическим выражением работы изменения объема.

При переходе рабочего тела из состояния 1 в состояние 2 объем меняется от v₁ до v₂. Удельная работа, участвующая в процессе

. (2.2)

В

Рис. 2.2. Процесс 12 расширения рабочего тела в цилиндре с поршнем и совершенная им работа – площадь v₁12v₂v₁

pv-диаграмме площадь 12v₂v₁1 также равна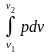 . Следовательно, в pv-диаграмме площадь, заключенная между кривой процесса 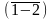крайними ординатам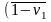и и 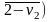и отрезком оси абсцисс 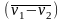, в определенном масштабе равна удельной работе процесса.

Д

Рис. 2.3. График зависимости

работы расширения от процесса

опустим, расширение газа происходит тремя разными процессами (а, b, с) при одних и тех же начальном (1) и конечном (2) состояниях (рис. 2.3). Площадь, изображающая работу под кривой а, больше, чем площадь, изображающая работу под кривой b. Площадь, изображающая работу под кривой b, больше, чем площадь, изображающая работу под кривой с.

Это значит, что l_а > l_b > l_с. То есть работа расширения, как и количество теплоты, зависит не только от начального и конечного состояний газа, но и от характера процесса перехода рабочего тела из одного состояния в другое. Работа не является параметром состояния. Работа связана с процессом. Нет процесса  нет работы.