

8.1. Правые и левые тройки векторов и системы координат. |
47 |
Лекция 8. Векторное произведение двух векторов: правые и левые тройки векторов и систем координат, геометрические свойства, алгебраические свойства, выражение векторного произведения в декартовой системе координат.
8.1.Правые и левые тройки векторов и системы координат.

 Определение.
Определение. 
 Три вектора называются упорядоченной тройкой (или про-
Три вектора называются упорядоченной тройкой (или про-
сто тройкой), если указано, какой из этих векторов является первым, какой - вторым и какой - третьим.
При записи тройки векторов мы всегда будем располагать эти векторы в порядке их следования. Так, запись bac означает, что первым элементом тройки является вектор b, вторым - вектор a и третьим - вектор c.

 Определение.
Определение. 
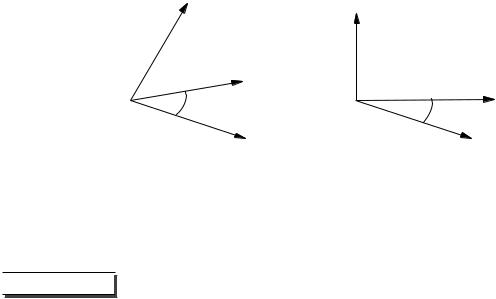
 Тройка не компланарных векторов abc называется правой (левой), если выполнено одно из следующих трех условий:
Тройка не компланарных векторов abc называется правой (левой), если выполнено одно из следующих трех условий:
1.если, будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки;
2.если после приведения к общему началу вектор c располагается по ту сторону от плоскости, определяемой векторами a и b, откуда кратчайший поворот от a к b кажется совершающимся против часовой стрелки (по часовой стрелке);
3.если, находясь внутри телесного угла, образованного приведенными к общему началу векторами a, b, c, мы видим поворот от a к b и от него к c совершающимся против часовой стрелки (по часовой стрелке).
Легко проверить, что условия 1, 2 и 3 эквивалентны между собой. Заметим также, что понятие правой и левой тройки теряет смысл для компланарных векторов.
Если две тройки векторов либо обе являются правыми, либо обе являются левыми, то говорят, что эти тройки одной ориентации. В противном случае говорят, что рассматриваемые две тройки противоположной ориентации.
Всего из трех векторов a, b и можно составить следующие шесть троек:
abc, bca, cab,
bac, acb, cba.
Тройки abc, bca, cab - правые, а bac, acb, cba - левые.
48
Пример:
c
c
b |
a |
|
|
a |
b |
|
Правая тройка векторов ABC. Левая тройка векторов ABC.
Рис. 10. Упорядоченные тройки векторов.
8.2. Векторное произведение двух векторов.

 Определение.
Определение. 
 Векторным произведением вектора на вектор b называ-
Векторным произведением вектора на вектор b называ-
ется вектор c, обозначаемый символом c = [ab] = a × b и удовлетворяющий следующим трем требованиям:
1)длина вектора c равна произведению длин векторов a и b на синус угла ϕ между ними , т. е. |c| = |[ab]| = |a| |b| SIN ϕ;
2)вектор c ортогонален к каждому из векторов a и b;
3)вектор c направлен так, что тройка векторов abc является правой.
Всоответствии с договоренностью, в качестве угла между векторами
берем тот угол ϕ, который не превосходит π. При этом всегда SIN ϕ > 0 и величина |c| неотрицательна. Из формулы |c| = |[ab]| = |a| |b| SIN ϕ следует также, что в случае коллинеарных векторов a и b определяемый вектор c = [ab] является нулевым.
Понятие векторного произведения широко используется в механике. Если вектор b изображает приложенную в некоторой точке M силу, а вектор a идет из некоторой точки O в точку M, то вектор c = [ab] представляет собой момент силы b относительно точки O.
8.3. Геометрические свойства векторного произведения.
Справедлива следующая теорема.
Теорема 8.1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Доказательство. 1). Необходимость вытекает из самого определения векторного произведения: для коллинеарных векторов a и b векторное произведение по определению равно нулю.

8.3. Геометрические свойства векторного произведения. |
49 |
2). Достаточность. Пусть векторное произведение [ab] равно нулю. Докажем, что векторы a и b коллинеарны. Прежде всего исключим тривиальный случай, когда хотя бы один из векторов a или b является нулевым (нулевой вектор имеет неопределенное направление, и его можно считать коллинеарным любому вектору). Если же оба вектора a и b ненулевые, то |a| > 0 и |b| > 0, и поэтому, из равенства [ab] = 0 и из формулы векторного произведения вытекает, что SIN ϕ = 0, т. е. векторы a и b коллинеарны.
Теорема 8.2. Длина (или модуль) векторного произведения [ab] равняется площади S параллелограмма, построенного на приведенных к общему началу векторах а и b.
Доказательство. Так как площадь параллелограмма равна произведению смежных сторон этого параллелограмма на синус угла между ними, то теорема непосредственно вытекает из формулы |c| = |[ab]| =
|a| |b| SIN ϕ.
Чтобы получить следствие из этой теоремы, введем понятие орта.

 Определение.
Определение. 
 Ортом произвольного ненулевого вектора с назовем единичный вектор, коллинеарный с и имеющий одинаковое с с направление.
Ортом произвольного ненулевого вектора с назовем единичный вектор, коллинеарный с и имеющий одинаковое с с направление.
Следствие из теоремы.
Если e - орт векторного произведения [ab], a S - площадь параллелограмма, построенного на приведенных к общему началу векторах а и b, то для векторного произведения [ab] справедлива следующая формула:
[ab] = Se.
Замечание. Из определений орта и векторного произведения вытекает, что тройка abe является правой (т.к. тройка ab[ab] является правой).
Следующее свойство устанавливает важную для дальнейшего формулу.
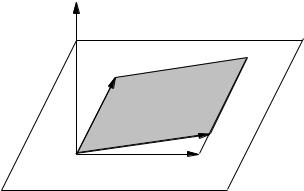
Теорема 8.3. Если с - какой-нибудь вектор, π - любая содержащая его плоскость, е - единичный вектор, лежащий в плоскости π и ортогональный к c, g - единичный вектор, ортогональный к плоскости π и направленный так, что тройка ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула
[ac] = прEa · |c|g. |
(8.1) |
Доказательство. Достаточно доказать, что векторы, стоящие в левой
иправой частях (8.1):
1)имеют одинаковую длину,
2)коллинеарны,
50
3) имеют одинаковое направление.
В силу соотношения |[ac]| = S, где S - площадь построенного на приведенных к общему началу векторах а и с параллелограмма. Длина вектора, стоящего в правой части (8.1), равна |c||прEa|, т. е. тоже равна S, т.к. если за основание указанного параллелограмма принять вектор c, то его высота h будет равна |прEa|.
|
g |
|
|
|
|
c |
|
|
|
|
a |
|
O |
|
e |
π |
|
h |
|
|
|
||
|
|
|
|
|
Рис. 11. К доказательстве теоремы 8.3 |
||
Коллинеарность векторов, стоящих в левой и правой частях (8.1), вытекает из того, что оба эти вектора ортогональны (см. рис. 11) к плоскости π (вектор [ас] в силу определения векторного произведения, а вектор |прEa| · |c|g в силу того, что вектор g по условию ортогонален к плоскости π).
Остается проверить, что векторы, стоящие в левой и правой частях (8.1), одинаково направлены. Для этого достаточно заметить, что векторы [ас] и g одинаково направлены (противоположно направлены), когда тройка acg является правой (левой), т. е. когда векторы а и е лежат по одну сторону от с (по разные стороны от с)) и проекция прEa является положительной (отрицательной), но это и означает, что векторы [ас] и прE · |c|g всегда одинаково направлены.
8.4. Алгебраические свойства векторного произведения.
Векторное произведение векторов обладает следующими четырьмя свойствами:
1.[ab] = - [ba] (свойство антиперестановочности сомножителей);
2.[(αa)b] = α[ab] (сочетательное свойство относительно числового множителя );
3.[(a+b)c] = [ac]+[bc] (распределительное свойство относительно суммы векторов );
4.[aa] = 0 для любого вектора а.
8.4. Алгебраические свойства векторного произведения. |
51 |
Убедимся в справедливости этих свойств.
Для доказательства свойства 1 положим c = [ab], d = [ba]. Если векторы а и b коллинеарны, то в силу определения векторного произведения c = d = 0, и свойство 1 доказано. Если же а и b не коллинеарны, то векторы с и d, во-первых, имеют одинаковую длину (в силу формулы для длины векторного произведения) и, во-вторых, коллинеарны (в силу того, что оба вектора c и d ортогональны к плоскости, определяемой векторами a и b). Но тогда либо c = d, либо c = - d. Если бы имела место первая возможность, то по определению векторного произведения обе тройки abc и bac оказались бы правыми, но это невозможно, т.к. эти тройки противоположной ориентации. Итак, с = - d, и свойство 1. полностью доказано.
Для доказательства свойства 2 положим c = [(αa)b], d = α[ab] и прежде всего исключим тривиальные случаи, когда вектор а коллинеарен b или когда а = 0. В этих случаях мы получим, что с = d = 0, и свойство 2 доказано. Пусть теперь векторы а и b не коллинеарны и α 6= 0. Докажем, что и в этом случае векторы с и d равны. Обозначим буквой ϕ угол между векторами а и b, а буквой ψ угол между векторами αa и b. По определению длины векторного произведения и произведения вектора на число можно утверждать, что |c| = |α||a||b| SIN ϕ, |d| = |α||a||b| SIN ψ. Учтем теперь, что могут представиться два случая: 1). ψ = ϕ (когда α > 0 и векторы a и αa направлены в одну сторону); 2). ψ = π − ϕ (когда α < 0 и векторы а и αa направлены в противоположные стороны. В обоих случаях SIN ϕ = SIN ψ и в силу формул |c| = |α||a||b| SIN ϕ, |d| = |α||a||b| SIN ψ, получаем |c| = |d|, т. е.векторы c
иd имеют одинаковую длину. Далее, очевидно, что векторы c и d коллинеарны, т.к. ортогональность к плоскости, определяемой векторами αa
иb, означает ортогональность и к плоскости, определяемой векторами a и b. Для доказательства равенства векторов c и d остается проверить, что эти векторы имеют одинаковое направление. Пусть α > 0 (α < 0) , тогда векторы а и αa одинаково направлены (противоположно направлены), и, стало быть, векторы [ab] и [(αab] также одинаково направлены (противоположно направлены), а это означает, что векторы d = α[ab] и c = [(αa)b] всегда одинаково направлены. Свойство 2. доказано.
Переходим к доказательству свойства 3. Рассмотрим отдельно два случая:
1)случай, когда векторы a, b и c компланарны;
2)случай, когда эти векторы не компланарны.
В первом случае векторы a, b и c, будучи приведены к общему началу, располагаются в одной плоскости, которую мы обозначим буквой π. Пусть e - единичный вектор, принадлежащий плоскости π и ортогональный к вектору c, a g - единичный вектор, ортогональный к плоскости π и такой, что тройка ecg является правой. Согласно теореме о свойствах векторного произведения
52
[ac] = прEa · |c|g, [bc] = прEb · |c|g,
[(a + b)c] = прEa + b · |c|g.
Свойство 3 непосредственно вытекает из последних трех формул и из линейного свойства проекции прEa + прEb = прEa + b.
Пусть теперь векторы a, b и c не компланарны. Так как три вектора [(a + b)c], [ac] и [bc] ортогональны к вектору c, то эти три вектора компланарны, а стало быть линейно зависимы. Но это означает, что найдутся такие числа α, β и γ, хотя бы одно из которых не равно нулю, так что справедливо равенство
α[(a + b)c] = β[ac] + γ[bc]. |
(8.2) |
Остается доказать, что α = β и α = γ. Докажем, например, что α = β. Для этого, пользуясь уже доказанным распределительным свойством скалярного произведения, умножим равенство (8.2) скалярно на вектор b и учтем, что произведение [bc]b равно нулю. В результате получим α[(a + b)c]b = β[ac]b. Поскольку векторы a, b и c не компланарны, произведение [ac]b не равно нулю, и для доказательства равенства α = β достаточно доказать равенство произведений [(a + b)c]b и [ac]b. Равенство абсолютных величин указанных произведений вытекает из того, что абсолютные величины этих векторов равны объемам двух параллелепипедов с равновеликими основаниями.
Равенство знаков указанных произведений вытекает из определения правой (левой) тройки: очевидно, что тройки acb и (a + b)cb одной ориентации. Равенство α = β доказано. Аналогично (посредством умножения (8.2) скалярно на вектор a доказывается равенство α = γ Свойство 3 полностью доказано.
Остается доказать свойство 4, утверждающее, что векторный квадрат любого вектора равен нулю, но это свойство непосредственно вытекает из определения векторного произведения и из того, что любой вектор a коллинеарен сам с собой.
Отметим, что свойства 2 и 3 сформулированы применительно к первому сомножителю векторного произведения. Аналогичные свойства справедливы и применительно ко второму сомножителю векторного произведения, т. е. можно утверждать, что
[a(αb)] = α[ab] и [a(b + c)] = [ab] + [ac]. |
(8.3) |
Доказанные свойства имеют фундаментальное значение. Они позволяют при векторном перемножении векторных многочленов выполнять действия почленно и производить сочетание числовых множителей (но при этом необходимо либо сохранять порядок векторных множителей, либо при изменении этого порядка менять знак на противоположный).

8.5. Векторное произведения в декартовых координатах. |
53 |
8.5. Векторное произведения в декартовых координатах.
Теорема 8.4. Если два вектора a и b определены своими декартовыми прямоугольными координатами
a = {x1, y1, z1}, b = {x2, y2, z2}, |
|
то векторное произведение этих векторов имеет вид |
|
[ab] = {yLz2 − y2z1, z1x2 − z2xL, x1y2 − x2y1}, |
(8.4) |
или
i j k
[ab] = |
x1 |
y1 |
z1 |
|
(8.5) |
|
x2 |
y2 |
z2 |
|
|
|
|
|
Раскрывая определитель (8.5), по элементам первой строки, получаем разложение вектора [ab] по базису i, j, k.
Доказательство. Составим из тройки базисных векторов i, j и k все возможные пары и для каждой из пар подсчитаем векторное произведение. Учитывая, что базисные векторы взаимно ортогональны, образуют правую тройку и имеют единичную длину, получим:
[ii] = 0, [ij] = k, [ik] = - j,
[ji] = - k, [jj] = 0, [jk] = i,
[ki] = j,
[kj] = -i, (8.6) [kk] = 0.
Далее, принимая во внимание, что a = x1i+ y1j+ z1k, b = x2i+ y2j+ z2k, получим
[ab] = x1x2[ii] + x1y2[ij] + x1z2[ik]
+y1x2[ji] + y1y2[jj] + y1z2[jk]
+z1x2[ki] + z1y2[kj] + z1z2[kk]
= (yLz2 − y2z1)i + (z1x2 − z2xL)j + (x1y2 − x2y1)k
Теорема доказана.
Следствие.
Если два вектора a = {x1, y1, z1} и b = {x2, y2, z2} коллинеарны, то координаты их пропорциональны, т. е.
x1 = y1 = z1 x2 y2 z2
Заметим, что в знаменателях последних равенств могут стоять нули. Чтобы обойти эту трудность, мы договоримся всякую пропорцию a/b = c/d понимать в смысле равенства ad = bc. Для доказательства следствия достаточно заметить, что из равенства нулю векторного произведения и из формулы (8.5) вытекают равенства
y1z2 = y2z1, z1x2 = z2x1, x1y2 = x2y1,
54
которые в силу сделанного выше замечания эквивалентны доказываемым пропорциям.
