

50 |
Оглавление |
Лекция 9. Линейная зависимость векторов (линейные комбинации двух, трех и четырех векторов). Проекция вектора на ось и ее свойства.
9.1. Линейная зависимость векторов
Вначале рассмотрим часто используемые понятия коллинеарности и компланарности векторов.
 Определение.
Определение.  Два вектора, параллельные одной и той же прямой, называются
Два вектора, параллельные одной и той же прямой, называются
коллинеарными.
 Определение.
Определение.  Три вектора, параллельные одной и той же плоскости, называются
Три вектора, параллельные одной и той же плоскости, называются
компланарными.
Нулевой вектор считается коллинеарным любому другому вектору. Нулевой вектор считается компланарным любой паре векторов.

 Определение.
Определение. 
 Выражение вида α1a1 +α2a2 +. . .+αnan, где αi; i = [1, n] - некоторые числа, называется линейной комбинацией векторов a1, a2, . . . an.
Выражение вида α1a1 +α2a2 +. . .+αnan, где αi; i = [1, n] - некоторые числа, называется линейной комбинацией векторов a1, a2, . . . an.

 Правило суммирования.
Правило суммирования. 
 В тех случаях, когда явная запись суммы некоторого числа слагаемых
В тех случаях, когда явная запись суммы некоторого числа слагаемых
нецелесообразна или невозможна, но известно, как зависит значение каждого из слагаемых от его номера, то мы будем использовать форму записи операции суммирования:
N
X
F (n) + F (n + 1) + . . . + F (N) = F (k),
k=n
где k - индекс суммирования, n - минимальное значение индекса суммирования, N - максимальное значение индекса суммирования и F (k) - общий вид слагаемого.
Используя данное соглашение о суммировании, линейную комбинацию α1a1 + α2a2 + . . . + αnan можно записать в виде
n |
|
X |
|
α1a1 + α2a2 + . . . + αnan = αiai. |
(9.1) |
i=1
Рассмотрим теперь определение важного понятия линейной зависимости системы векторов.

 Определение.
Определение. 
 Векторы a1, a2, . . . an называются линейно зависимыми, если суще-
Векторы a1, a2, . . . an называются линейно зависимыми, если суще-
|
n |
|
X |
ствует их нетривиальная линейная комбинация |
αiai такая, что |
|
i=1 |
n |
|
X |
|
αiai = 0. |
(9.2) |
i=1 |
|

9.1. Линейная зависимость векторов |
51 |

 Определение.
Определение. 
 Векторы a1, a2, . . . an называются линейно независимыми, если из
Векторы a1, a2, . . . an называются линейно независимыми, если из
n
X
условия αiai = 0 следует тривиальность линейной комбинации
i=1
n
X
αiai = 0, то есть, что α1 = α2 = . . . = αn.
i=1
Справедливы следующие утверждения:
Теорема 9.1. Один вектор линейно зависим тогда и только тогда, когда он нулевой.
Теорема 9.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Теорема 9.3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Рассмотрим подробно теорему 9.3, доказав предварительно следующее вспомогательное утверждение:
Лемма 9.3. Для линейной зависимости векторов a1, a2, . . . an необходимо и достаточно, чтобы один из них был линейной комбинацией остальных.
Доказательство. Докажем необходимость. Пусть векторы a1, a2, . . . an линейно
зависимы, тогда существуют числа α1, α2, . . . αn, одновременно не равные нулю,
n
X
такие, что αiai = 0. Для определенности можно считать, что α1 6= 0, но
тогда |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 = |
n |
− α1 |
ai |
(9.4) |
|
|
|
|||||
|
|
X |
|
αi |
|
|
|
|
|
|
|
|
|
|
|
i=2 |
|
|
|
|
что и доказывает необходимость. |
|
|
|
|
n |
|
|
|
|
|
|
|
|
Докажем достаточность. Пусть, для определенности a1 = |
X |
|||||
αiai, тогда |
||||||
i=2
n
X
(−1)a1 + αiai = 0, причем | − 1| + |α2| + . . . + |αn| > 0. То есть нетривиальная
i=2 |
|
линейная комбинация векторов a1, a2, . . . an равна нулевому вектору. |
|
Докажем теперь теорему 9.3. |
|
Доказательство. Докажем необходимость. Пусть три вектора a1, a2, a3 линейно зависимы, то есть существуют три, одновременно не равных нулю, числа
α1, α2, α3, таких, что α1a1 + α2a2 + α3a3 = 0. Тогда, по лемме 9.3 один из векторов есть линейная комбинация двух остальных и, значит, данные три век-
тора компланарны. Докажем достаточность в предположении, что векторы a1 и a2 неколлинеарны. Пусть даны три компланарных вектора a1, a2, a3. Перенесем эти векторы таким образом, чтобы их начала попали в одну точку. Через конец вектора a3 проведем прямые, параллельные векторам a1 и a2. При этом получим пару векторов b1 и b2 таких, что a3 = b1 + b2. (см. рис. 13). Поскольку вектор b1 коллинеарен вектору a1, а вектор b2 коллинеарен вектору a2, по теореме 9.2 получаем, что b1 = α1a1; b2 = α2a2, но, с другой стороны, имеем
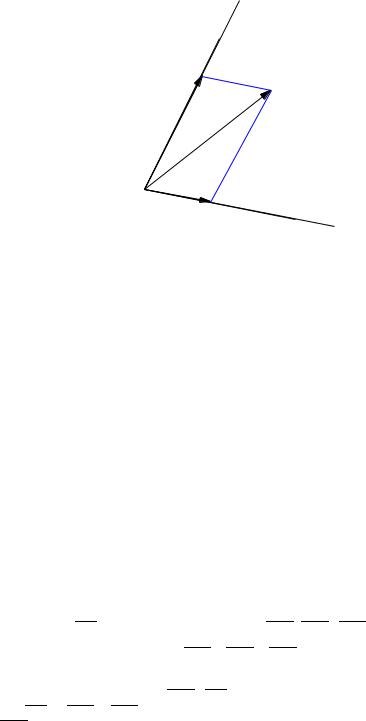
52 |
Оглавление |
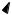 a1
a1
b1
a3
b2  a2
a2
Рис. 13. К доказательству теоремы 9.3
a3 = α1a1 + α2a2, и векторы a1, a2, a3 по лемме 9.3, линейно зависимы. Случай коллинеарных a1 и a2 рассматривается аналогично.
Рассмотрим теперь линейную зависимость четырех векторов.
Теорема 9.4. Любые четыре вектора линейно зависимы.
Доказательство. Прежде всего исключим случай, когда какая - нибудь тройка из указанных четырех векторов компланарна. Тогда в силу теоремы 9.3 указанная тройка векторов линейно зависима, а стало быть, и все четыре вектора линейно зависимы.
Остается рассмотреть случай, когда среди четырех векторов a1, a2, a3 и a4 никакая тройка векторов не компланарна (и, стало быть, нет ни одной пары коллинеарных векторов и ни одного нулевого вектора).
Приведем все четыре вектора a1, a2, a3 и a4 к общему началу O и проведем через конец вектора a4 плоскости, параллельные плоскостям, определяемым парами векторов a1a2, a1a3, и a2a3 (см. рис. 14). Точки пересечения указанных плоскостей с прямыми, на которых лежат векторы a1, a2 и a3 обозначим соответственно буквами A1, A2, A3. Существование указанных точек пересечения вытекает из того, что векторы a1, a2 и a3 не компланарны. Убедимся в том, что
вектор a4 = OD равен сумме трех векторов OA1, OA2и OA3, т. е. |
|
a4 = OA1 + OA2 + OA3. |
(9.5) |
Из правила параллелограмма сложения векторов и из параллелограмма OA3DE
(см. рис. 14) вытекает, a4 = OA3 +OE, а из параллелограмма OA2EA1 вытекает,
что OE = OA1 + OA2. Тем самым равенство 9.5 установлено. Так как вектор
OA1 коллинеарен ненулевому вектору a1 (с которым он лежит на одной прямой), то в силу теоремы 9.2 найдется вещественное число α1, такое, что
|
|
|
OA1 = α1a1. |
(9.6) |
|
|
9.2. Базис. Координаты вектора в базисе. |
53 |
|
|
|
|
D |
A3 |
|
a4 |
|
|
|
|
|
a3 |
A2 |
|
E |
|
|
||
|
|
|
|
a2 |
|
|
|
O |
a1 |
A1 |
|
|
Рис. 14. К доказательству теоремы 9.4 |
|
|
Аналогично вытекает существование вещественных чисел α2 и α3 таких, что
|
|
|
|
|
OA2 = α2a2, OA3 = α3a3. |
(9.7) |
|||
В результате получаем равенство
a4 = α1a1 + α2a2 + α3a3, |
(9.8) |
которое можно переписать в виде
α1a1 + α2a2 + α3a3 + (−1)a4 = 0. |
(9.9) |
Так как из четырех чисел α1, α2, α3, −1 одно заведомо отлично от нуля, то равенство (9.8) доказывает линейную зависимость векторов a1, a2, a3 и a4.
9.2. Базис. Координаты вектора в базисе.

 Определение.
Определение. 
 Базисом на прямой называется любой ненулевой вектор, принадле-
Базисом на прямой называется любой ненулевой вектор, принадле-

 Определение.
Определение. 


 Определение.
Определение. 

жащий этой прямой.
Базисом на плоскости называется любая упорядоченная пара линейно независимых векторов, принадлежащих этой плоскости. Базисом в пространстве называется любая упорядоченная тройка линейно независимых векторов.
Базис называется ортогональным, если образующие его векторы
попарно ортогональны (взаимно перпендикулярны).
Ортогональный базис называется ортонормированным, если обра-
зующие его векторы имеют единичную длину.
Базис, составленный из линейно независимых векторов a1, a2, a3, будем обозначать (a1, a2, a3) Ортогональный или ортонормированный базис будем обозначать как (e1, e2, e3).
54 |
Оглавление |
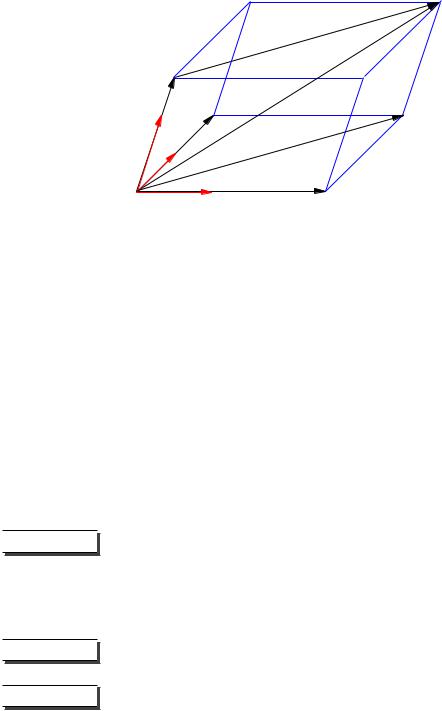
Теорема 9.5. Пусть дан базис (a1, a2, a3). Тогда любой вектор x может быть представлен, и притом единственным образом, в виде x = α1a1 + α2a2 + α3a3, где α1, α2, α3- некоторые числа.
Доказательство. Для доказательства совместим начала всех векторов a1, a2, a3 и x в точке O и проведем через конец вектора x плоскость, параллельную плоскости O, a1, a2 (рис. 15). Построим новые вектора y и z так, чтобы x = y+z,
a3
y
z
x
a2
O
a1
Рис. 15. К доказательству теоремы 9.5
a z и a3 были коллинеарны, тогда, в силу коллинеарности вектора z вектору a3, z = α3a3. Перенеся начало вектора y в точку O и рассуждая как при доказательстве теоремы 9.3, получим y = α1a1 + α2a3 и, следовательно,
x = α1a1 + α2a2 + α3a3. |
(9.10) |
что доказывает существование разложения. Докажем единственность разложения по базису. Пусть мы имеем
x = α1a1 + α2a2 + α3a3. |
(9.11) |
и предположим, что существует другая тройка чисел α01, α02, α03 таких, что
x = α10 a1 + α20 a2 + α30 a3. |
(9.12) |
Вычитая почленно эти равенства, получаем |
|
x = (α1 − α10 )a1 + (α2 − α20 )a2 + (α3 − α30 )a3 = 0. |
(9.13) |
где, в силу сделанного предположения о не единственности разложения,
|α1 − α10 | + |α2 − α20 | + |α3 − α30 | > 0. |
(9.14) |
Но это означает, что векторы α1, α2, α3 линейно зависимы и, следовательно, не могут быть базисом. Полученное противоречие доказывает единственность разложения.
Числа α1, α2, α3 - коэффициенты в разложении x = α1a1 + α2a2 + α3a3 называются координатами (или компонентами) вектора x в базисе (a1, a2, a3).
В координатном представлении операции с векторами имеют следующий вид:
9.3. Ортогональное проектирование. |
55 |
|
1. Два вектора x = α1a1 + α2a2 + α3a3 и y = β1a1 + β2a2 + β3a3 |
равны |
|
тогда и только тогда, когда равны их координатные представления: |
||
x = y, если α2 |
= β2 . |
(9.15) |
α1 |
= β1 |
|
|
|
|
α3 = β3
2.Координатное представление суммы двух векторов x = α1a1 + α2a2 + α3a3 и y = β1a1 +β2a2+β3a3 равно сумме координатных представлений слагаемых:
x + y = (β1 + α1)a1 + (β2 + α2)a2 + (β3 + α3)a3. |
(9.16) |
3.Координатное представление произведения вектора x = α1a1 + α2a2 + α3a3 на число λ равно произведению координатного представления вектора x на это число λ:
λx = (λα1)a1 + (λα2)a2 + (λα3)a3. |
(9.17) |
9.3. Ортогональное проектирование.
Прямую l, с расположенным на ней ненулевым вектором b, будем называть
осью.
Вектор b называется направляющим вектором оси l.
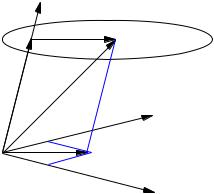
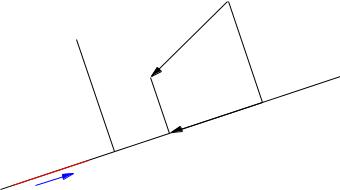
Пусть дана точка M , не лежащая на оси l, тогда основание перпендикуляра, опущенного из M на ось l точку M будем называть ортогональной проекцией точки M на ось.
M |
a |
l
прla
b  M e
M e
Рис. 16. Проекция точки и проекция вектора на ось
Примером оси может служить ось координат - прямая, проходящая через начало координат, направляющим вектором которой служит один из базисных векторов.
Ортогональной проекцией вектора a на ось l называется вектор прla, лежащий на оси l, начало которого есть ортогональная проекция начала вектора a на ось l, а конец - ортогональная проекция конца вектора a.
56 |
Оглавление |
Выполним нормировку направляющего вектора b, то есть заменим его на вектор
e = |
b |
(9.18) |
|b| |
и рассмотрим нормированный базис {e} на оси l (см. рис. 16).
Численным значением ортогональной проекции вектора a на ось l называется координата вектора прla а в базисе {e}.
Углом между ненулевыми векторами a и b называется величина наименьшего из двух углов, образуемых этими векторами при совмещении их начал.
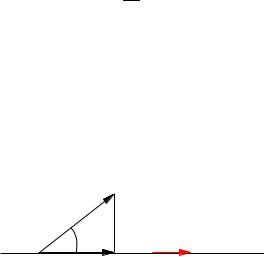
Численное значение ортогональной проекции вектора a на ось l обозначим как прla Из рис. 17 очевидно, что
прla = |a| cos ϕ, |
(9.19) |
где ϕ есть угол между a и e.
a
ϕ |
l |
|
прl a e
Рис. 17. Проекция вектора на ось
Свойства ортогональных проекций Проекция суммы двух векторов равна сумме проекций этих векторов.
Если вектор умножить на вещественное число, то его проекция также умножится на это число.
Проекция линейной комбинации векторов равна той же линейной комкомбинации проекций.
Справедливость этих свойств вытекает из определения операции ортогонального проектирования и правил действия с векторами.
Свойства численных значений ортогональных проекций:
прl(a1 + a2) = прl(a1) + прl(a2)
прl(α1a1) = α1прla1
прl(α1a1 + α2a2 + . . . + αnan =) = α1прla1 + α2прla2 + . . . + αnпрlan
Эти равенства следуют из свойств ортогональных проекций и свойств координат векторов.
