
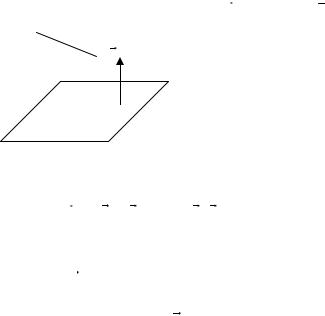
П : Аx + By + Cz + D = 0, П n = {A, B,C} ( n - нормаль к плоскости П )
l
n
П
рис 44.1 Возможные случаи взаимного расположения прямой и плоскости
l || П l n(т.е. a n ,или 0 = a n = Aα + Bβ + Cγ |
;) M0 П |
Aα + Bβ + Cγ = 0 |
||
Ax0 + By0 + Cz0 + D ≠ 0 |
||||
(44.1) |
|
|
|
|
l П l n ; M0 |
Aα + Bβ + Cγ = 0 |
|
|
|
П |
0 |
(44.2) |
|
|
|
Ax0 + By0 + Cz0 + D = |
|
|
|
l ∩ П (есть одна точка) l / n Aα + Bβ + Cγ ≠ 0 |
|
(44.3) |
|
|

Билет №27
Вопрос №1
Теорема Кронеккер-Капелли
13.1 Формулировка теоремы Кронеккер-Капелли
Теорема Кронеккер-Капелли: Для того, чтобы система линейных уравнений была совместна, необходимо и
достаточно, чтобы ранг её основной матрицы был равен рангу её расширенной матрицы.
|
|
a11x1 + a12 x2 +...+ a1n xn |
= b1 |
|
|
|
|
||||||||||
|
|
a21x1 + a22 x2 +...+ a2n xn |
= b2 |
|
|
|
(13.1) |
||||||||||
|
|
............................................. |
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x + a |
m2 |
x |
2 |
+...+ a |
mn |
x |
n |
= b |
|
|
|
|||
|
|
|
m1 1 |
|
|
|
|
|
|
m |
|
|
|
||||
a11 |
a12 ... |
a1n |
|
|
|
a11 |
|
a12 |
... |
a1n |
b1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 ... |
a2n |
|
|
|
a21 |
|
a22 |
... |
a2n |
b2 |
|
|||||
A = |
... |
... ... ... |
; |
|
|
B = |
... |
|
|
... ... ... ... |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
am2 ... |
|
|
|
|
|
|
|
|
|
am2 |
... |
amn |
|
|
|
am1 |
amn |
|
|
|
am1 |
|
bm |
||||||||||
13.2 Формулировка критерия определенности
Теорема (будет доказана в конце §19): Система линейных уравнений (13.1) определена (имеет единственное
решение) тогда и только тогда, когда ранг её матрицы равен рангу её расширенной матрицы и равен числу неизвестных.
|
|
13.3 Доказательство необходимости теоремы Кронеккер-Капелли |
||||||
(её достаточность будет доказана в конце §19) |
|
|
||||||
Отметим, что r(B)≥r(A), ибо если r(B)=k, то всякий M k+1 (B) = 0 . Но всякий M k+1 (A) |
является минором |
|||||||
матрицы В (ибо матрица А является частью матрицы В), и поэтому |
M k+1 (A) = M k+1 (B) = 0 . Поэтому по |
|||||||
лемме №2 из §11 r(А)≤k=r(В). |
|
|
|
|
||||
Итак, |
пусть |
r(А) ≠ r(В)=k |
(тогда |
|
r(А)<r(B)). Приведя матрицу |
В к ступенчатому |
виду, получим: |
|
a11' |
a12 ' |
... |
a1n ' |
b1' |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
a22 ' |
... |
a2n ' |
b2 ' |
|
|
|
|
... |
... |
... |
... |
... |
|
(под a ' будем обозначать преобразованные элементы матрицы А, а под |
||
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
... |
0 |
b(k 1) ' |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
нули |
|
0 |
|
|
|
|
bj ' – преобразованные элементы последнего столбца матрицы В).
При этом (k+1)-я строка матрицы В соответствует уравнению: 0 x1 + 0 x2 +...+ 0 xn = b(k+1) '≠ 0 , которое
противоречиво, и, следовательно, система (13.1) несовместна.
Итак, если r(A) ≠ r(B), то, система (13.1) несовместна, и поэтому для совместности системы линейных уравнений (13.1) должно быть выполнено r(А)=r(В).
Необходимость теоремы Кронеккер-Капелли доказана.
Вопрос №2
Смешанное произведение векторов и его свойство

|
|
|
|
27.1 Определение смешанного произведения |
|
|
|
|
R R |
Определение. Смешанным произведением векторов a,b,c называется величина |
||||
R |
R |
R |
R |
R |
(a |
,b,c)= [a |
× b] c |
(вектор [a ×b]-векторное произведение скалярно умножается на третий вектор c |
|
|
|
|
|
27.2 Геометрический смысл смешанного произведения |
|
R |
R |
R R |
|
Если (a,b,c)> 0, значит векторы a,b,c образуют правую систему (т.е. имеют такую же ориентацию, как
соответственно большой, указательный, и пальцы правой руки и её ладони)
R |
R |
R |
R |
Если (a,b,c)< 0, значит векторы |
a,b,c образуют левую систему (аналогично для пальцев и ладони |
||
левой руки).
R
a × b
В1
D1
С
A1
сB
с D
b
О
a A
|
|
|
|
|
|
|
Рис. 27.1 |
||
|
|
|
|
|
|
|
R |
R R |
|
|
|
|
|
|
|
|
|||
Абсолютная величина смешанного произведения |
(a,b,c) |
-это объём паралелепипида OADBCA1D1B1 |
|||||||
|
|
|
|
|
R |
R |
|
|
|
стороны которого составляют вектора |
a,b,c |
|
|
||||||
В самом деле по определению ( см. 23.6) |
|
|
|
|
|||||
R |
R |
R |
R |
R |
R |
(27.1) |
|
|
|
(a |
,b,c)= [a |
× b] c |
= [a × b] Пр a |
b c |
|
|
|
||
|
|
|
|
R |
R |
|
|
|
|
Однако первый множитель в правой части равенства (27.1) это площадь параллелограмма OADB (см условие 2)определения векторного произведения (§25.1, 25.1)т.е. площадь основания паралелелипипеда
R |
× b)опускаемый на |
OADBCA1D1B1 . Проекция третьей стороны паралелепипеда на перпендикуляр (a |
основание OADB (см. условие 1) (определение векторного произведения в начале параграфа 25) – это опущенная на OADB высота данного паралелепипеда. Поэтому их произведение-это объём паралелепипеда
27.3 Свойства смешанного произведения
R |
R |
R |
R R |
R |
|
|
1. (a,b,c )= -(b,a,c )-перестановка сомножителей меняет знак. |
||||||
R |
R |
R |
R |
|
|
|
(a,b,c)= −(a |
,c,b) |
|
||||
R |
|
R |
R |
|
R |
|
(a,b,c)= −(c |
,b,a) |
|
||||
R R |
R |
R |
R |
R |
R R |
R |
(a,b,c)= (b,c,a) |
= (c,a,b )- циклическая замена не меняет знак. |
|||||

R |
R |
|
R |
R |
R |
R |
R |
2. (a1 |
+ a |
2 ,b,c) = |
(a1 |
,b,c) + (a2 |
,b,c) |
||
R |
|
R |
R |
|
R |
|
|
3. (λa |
,b,c) = λ(a |
,b,c) |
|
|
|||
Эти свойства доказаны в конце §28 |
|
|
||
|
27.4Необходимое и достаточное условие компланарности трех векторов |
|||
R |
R |
R |
R |
|
Теорема {a |
,b,c}- компланарная тогда и только тогда когда (a,b,c)= 0 |
|
||
Доказательство: |
|
|
|
|
R |
R |
|
|
|
Если {a,b,c}компланарные , то паралелепипед OADBCA1D1B1 |
имеет нулевой объем |
(см. Рис 27.1)т.е. |
||
|
R R |
}= 0 , Справедливо рассуждение и в обратную сторону, что читателю предлагается |
||
получим , что {a,b,c |
||||
провести самостоятельно.
Вопрос №3
Угол между прямой и плоскостью. Условие их перпендикулярности
|
|
|
Заметим, что sin (l;П) = cos (l;n) = cos (a,n) (см. рис. 44.2) Поэтому (см. формулу (24.11)) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(a |
|
n) |
= |
|
|
Aα + Bβ + Cγ |
|
|
|
|
= cos( |
|
, |
|
|
|
) = cos(l |
|
) = sin(l Π) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n |
n |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
l |
|
|
|
|
n |
a |
|
n |
|
|
|
A2 + B2 + C2 α 2 + β 2 + γ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
Мы показали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aα + Bβ + Cγ |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(l;П) = arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(44.4) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
2 |
+ |
|
B |
2 |
+ C |
2 |
|
|
|
α |
2 |
+ β |
2 |
+ γ |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
П |
|
|
|
|
|
|
|
|
|
|
|
В частности |
l П l || n α = |
β |
= |
γ |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
B |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
рис 44.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44.3 Точка пересечения прямой и плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Если задано общее уравнение прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
A x + |
|
|
y + C z + D = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
L 1 |
|
1 |
1 |
|
1 |
|
|
|
|
|
|
(37.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
A2x + B2 y + C2z + D2 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
то для того, чтобы найти точку пересечения прямой L с плоскостью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
П : Ax+By+Cz+D=0 |
(36.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
надо уравнение плоскости П приписать к системе уравнений (37.3) задающих прямую линию L , и решить полученную систему из трёх линейных уравнений с тремя неизвестными. Решение этой системы и будет координатами точки пересечения прямой L и плоскости П .
Если прямая L задана каноническим уравнением |
x − x0 |
= |
y − y0 |
= |
z − z0 |
(40.2), |
|
α |
β |
γ |
|||||
|
|
|
|
то для нахождения точки пересечения этой прямой с плоскостью П , заданной уравнением (36.4), уравнение (40.2) целесообразно перевести в параметрическое уравнение той же прямой (см. §40).
x = x0 +αt |
|
y = y0 + βt |
(40.4) |
z = z0 + γt |
|
Далее в линейное уравнение (36.4) вместо x, y ,z подставляем их выражения через параметр t по формуле (40.4). Получим некоторое линейное уравнение относительно t. Решим данное уравнение (относительно t), и найденное t подставим в формулу (40.4)Полученные после подстановки в (40.4) величины x, y, z и будут координатами точки пересечения прямой L , заданной уравнением (40.2) или (40.4) и плоскостью
В качестве примера рассмотрим задачу о том, как из точек M (x , y , z ) на плоскость П , заданную
уравнением 36.4, опустить перпендикуляр (т.е. как найти проекцию точки M на плоскость П ), а также докажем формулу (39.1) расстояния от точки до плоскости.

Билет №28
Вопрос №1
Системы n линейных уравнений с n неизвестными их решение с помощью обратной матрицы
a11x1 + a12 x2 +...+ a1n xn |
= b1 |
|
|||||||||
a21x1 + a22 x2 +...+ a2n xn |
= b2 |
(7.1) |
|||||||||
............................................. |
|||||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
x + a |
n2 |
x |
2 |
+...+ a |
nn |
x |
n |
= b |
|
|
|
n1 1 |
|
|
|
n |
|
|||||
(Система (7.1): n-уравнений с n неизвестными) |
|
||||||||||
Соответствующее матричное уравнение имеет вид: A x = b |
|
|
|
(7.2) |
|
||||||
Если матрица системы А не вырождена, то у нее существует обратная матрица A−1 . Умножая обе части |
|||||||||||
уравнения (7.2) слева на матрицу A−1 , получим: A−1 (A x) = (A−1 A) x = A−1 b , т.е. |
|
||||||||||
|
|
|
x = A−1 × b |
|
|
(7.3) |
|||||
Мы показали, что справедлива теорема 7.1. Если матрица системы невырожденная, то система определена и её решение можно найти по формуле (7.3). Формула (7.3) даёт решение системы (7.1) с помощью обратной
матрицы.
|
|
x + 2y = 2 |
|
|
|
|
|
|
|
||||
Рассмотрим пример: |
|
|
|
|
. |
|
|
|
|
|
|
||
|
|
3x + 4y = −4 |
|
|
|
|
|
|
|||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
−1 |
|
Матрица системы: A = |
|
|
; тогда обратная матрица (см. пример в §5, п. 5.10): A |
|
|||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
−8 |
|
|
|
|
|
из (7.3) имеем: |
x |
= A |
−1 |
|
2 |
|
|
, т.е. |
x = –8; |
y =5 (умножение матрицы |
|||
|
|
|
|
|
= |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
− 4 |
|
|
5 |
|
|
|
|
|
предлагаем читателю провести самостоятельно).
Вопрос №2
= |
− 2 |
1 |
|
|
|
||
|
|
|
|
|
. Тогда |
||
|
|
1.5 |
− 0.5 |
|
|
|
|
|
|
|
|
|
|||
A |
−1 |
на столбец |
|
2 |
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4 |
Скалярное произведение векторов и его свойства
Определение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R R |
R R |
|
|
|
R |
|
|
R |
|
|
R |
|
|
R |
|
R R |
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a b = (a,b) |
= |
|
a |
|
× ПрaRb |
= |
|
a |
|
|
b |
|
cos(a,b) = |
|
b |
|
ПрbRa (23.6) – скалярное произведение |
|||
|
|
|
|
|||||||||||||||||
R R |
|
|
R |
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|||
|
|
aЧb |
|
|
aЧb |
|
|
|
|
|
||||||||||
a^b = arcos R |
|
|
R |
;Прb = |
|
|
|
R |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aЧb |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства скалярного произведения:
RR
5)a b = b a
R R R R
6) (a1 + a2 ) b = a1 b + a2 b
R R
7) (λa) b = λ(a b)
8) (a,a) ≥ 0;(a,a) = 0 a = 0
Величина (a,a) называется скалярным квадратом вектораa . По определению: |
||||||||||||
R |
R |
R |
2 |
R |
= |
R |
aR |
|
|
|
|
|
a a = |
a |
a |
a a |
|
|
|
|
|
||||
(23.9) |
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство 2-го свойства: |
|
|
|
|
||||||||
R |
R |
|
|
R |
R |
R |
R |
R |
R |
|
||
(a |
1 + a2 ) b = ПрbR |
(a1 |
+ a |
2 ) b = b ПрbR a1 |
+ b ПрbR a2 |
= a1 |
b + a2 |
b |
||||
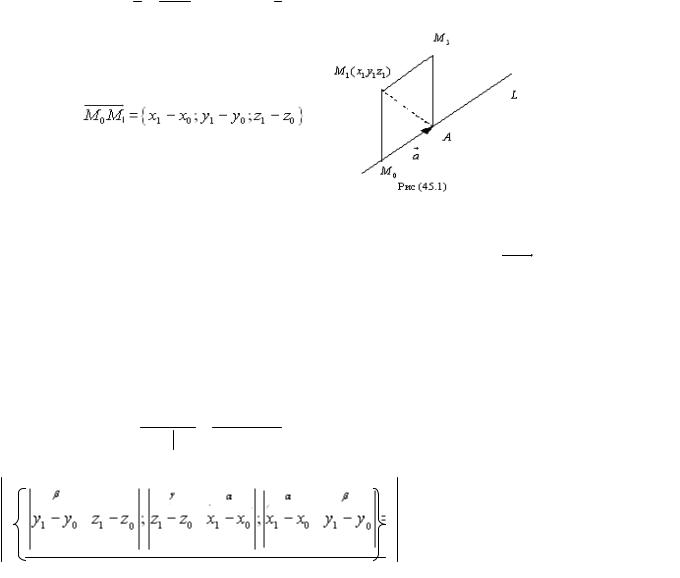
Доказательство 3-го свойства:
R |
R |
|
R |
|
ПрR |
R |
|
|
R |
|
|
R |
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(λ a) b = |
|
b |
|
(λa) = λ |
|
b |
|
ПрR (a) = λ(a |
|
b) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
Условие ортогональности 2-х векторов: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
R |
R |
|
|
|
R |
R |
= π |
|
|
|
|
R |
R |
R |
|
R |
|
|
|
R |
|
R |
b = 0 . |
Если a |
b a |
^b |
cos(a |
^b) = |
0 a |
b |
= 0 . Вывод a |
b a |
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вопрос №3 |
|
|
|
||||
Расстояние от точки до прямой в пространстве |
|
|
|
||||||||||||||||||||
Дано: точка M1(x1; y1; z1) и прямая L : |
x − x0 |
= |
|
y − y0 |
= |
z − z0 |
L M0 (x0 ; y0 ; z0 ) ( M0 -одна из |
||||||||||||||||
|
β |
γ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|||
точек на прямой L). L
 a = M0 A = {α;β;γ } ( a -направляющий вектор прямой L)
a = M0 A = {α;β;γ } ( a -направляющий вектор прямой L)
Расстояние от точки M1 до прямой L( ρ(M , L) ) совпадает с высотой ( hM0M1M2 A ) параллелограмма M0M1M2 A (см. рис
45.1), которая равна отношению площади ( SM0M1M2 A ) этого параллелограмма и длины основания M0 A. Далее у параграфов 25,26 и 24 (формула (24.10) имеем (см. также условие 2) векторное произведение.
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0M1 |
|
|
||||
p(M , L) = h |
|
|
= |
SM M |
M |
A |
= |
|
a |
|
= |
|||||
0M1M |
2 A |
0 |
R1 |
2 |
|
|
|
|
|
R |
|
|
||||
|
|
|
|
|
|
|
||||||||||
M |
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
γ
|a|
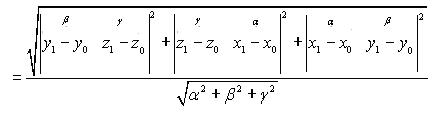 (45.1)
(45.1)
Билет №29
Вопрос №1
Формула Крамера
Рассмотрим систему:
a11 x1 + a12 x2 + ... + a1k−1 xk−1 + a1k xk + a1k+1 xk+1 + ... + a1n xn = b1 |
|
|
a21 x1 + a22 x2 + ... + a2k−1 xk−1 + a2k xk + a2k+1 xk+1 + ... + a2n xn |
= b2 |
|
............................................................................................... |
|
(8.1) |
|
|
|
an1 x1 + an2 x2 + ... + ank−1 xk−1 + ank xk + ank+1 xk+1 + ... + ann xn |
= bn |
|
|
|
|
|
a11 |
a12 |
... a1k−1 |
a1k |
a1k+1 |
... |
a1n |
|
||
|
|
= |
a21 |
a22 |
... a2k−1 |
a2k a2k+1 |
... |
a2n |
|
||||
|
|
|
|
... ... ... ... |
|
... |
|
... |
... ... |
|
|||
|
|
|
|
an1 |
an2 |
... ank−1 |
ank |
ank+1 |
... |
ann |
|
||
|
b1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
||
Заменим k-й столбец на столбец |
... |
свободных коэффициентов; |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn |
|
|
|
|
|
|
|
|
|
|
||
|
|
a11 a12 ... a1k−1 b1 |
a1k+1 ... |
a1n |
|
|
|||||||
|
|
|
|
||||||||||
получим определитель k |
= |
a21 a22 ... |
a2k−1 b2 |
a2k+1 ... |
a2n |
(k = 1, 2, …, n); |
|||||||
|
|
... ... ... |
... |
... |
|
... |
... ... |
|
|
||||
|
|
an1 an2 ... ank−1 bn |
ank+1 ... |
ann |
|
|
|||||||
|
умножим далее первое уравнение (8.1) на |
A1k ; |
|
|
|||||||||
|
|
|
|
|
2-е уравнение (8.1) на A2k ; |
|
|
|
|
||||
|
|
|
|
|
3-е уравнение (8.1) на |
A3k ; |
|
|
|
|
|||
|
|
|
|
|
|
…; |
|
|
|
|
|
|
|
|
|
|
|
|
n-ое уравнение (8.1) на |
Ank |
|
|
|
|
|||
и затем, суммируя уравнения системы (складываем по столбцам), получим:
(8.2)
(8.3)
(A1k a11 + A2k a21 + ...+ Ank an1 )x1 + (A1k a12 + A2k a22 |
+ ...+ Ank an2 )x2 + ...+ |
|
|
|||
+ (A1k a1k−1 |
+ A2k a2k−1 |
+ ...+ Ank ank−1 )xk−1 + (A1k a1k |
+ A2k a2k + ...+ Ank ank )xk |
+ |
(8.4) |
|
+ (A1k a1k+1 |
+ A2k a2k+1 |
+ ...+ Ank ank+1 )xk+1 + ... + (A1k a1n + A2k a2n + ...+ Ank ann )xn = |
||||
|
||||||
= b1 A1k + b2 A2k + ...+ bn Ank
Коэффициентом при xj в левой части уравнения (8.4) является сумма произведений элементов j-го столбца
определителя (j = 1, 2, …, n) на алгебраические дополнения k-го столбца, которые равны нулю, если j≠k (см. 12-е свойство определителя; §2) и самому определителю Δ, если j=k (см. 11-е свойство определителя; §2).
Правая же часть равенства (8.4) — разложение по k-му столбцу определителя |
k . Получим равенства: |
|||
xk = |
k |
(k = 1, 2, …, n) |
(8.5) |
|
Если Δ≠0, то поделив все равенства (8.5) на Δ, получим: |
|
|
|
|
xk |
= |
k |
|
(8.6) |
|
|
|||
Определение: Равенства (8.6), где k = 1, 2, …, n, называются формулами Крамера.

Отметим, что если Δ=0, а хотя бы одно из k ≠0, |
(8.7) |
то тогда k-е равенство в (8.5) будет противоречивым, и поэтому в этом случае система (8.1) несовместна.
x + y + z =1
На примере системы: 2x + 2y + 2z = 2 читателю предлагается самостоятельно доказать, что условие (8.7)
3x + 3y + 3z = 0
достаточно для несовместности системы (8.1), но для n ≥ 3 не является необходимым.
Вопрос №2
Вычисление скалярного произведения векторов через координаты сомножителей
24.1 Вычисление скалярного произведения через координаты сомножителей
Пусть |
|
= {a1,a2 ,a3} = a1i + a2 |
j + a3 k |
|
|
|
|
= {b1 ,b2 ,b3} = b1i + b2 |
j + b3 k |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
b |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
R |
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
R R |
|
R |
|
|
|
|
|
|
|
|
|
R R |
|
R |
|
|||||||||||||||
ab |
= (a1i |
+ a2 j |
|
+ a3k)(b1i |
|
+ b2 j + b3k) |
= a1i (b1i |
|
+ b2 j |
|
+ b3k) + a2 j(b1i + b2 j + b3k) + |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
R |
|
R |
|
|
|
|
R |
|
|
|
R |
|
|
|
|
|
R R |
|
|
|
|
|
R R |
|
|
|
|
|
|
|
R R |
|
|
|
|
|
|
R R |
|
R R |
R R |
|||||||||||||||
+ a3k(b1i |
+ b2 j |
|
+ b3k) = a1b1(i ,i ) + a1b2 (i , j) + a1b3 (i ,k) + a2b1( j,i ) + a2b2 ( j, j) + a2b3( j,k) + |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
R R |
|
|
|
|
|
|
|
R R |
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a3b1(k,i ) |
+ a3b2 (k, j) + a3b3 (k,k) = a1b1 + a2b2 |
+ a3b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
RR |
|
R |
|
2 |
|
|
RR |
|
R |
|
2 |
|
RR |
= |
|
R |
|
2 |
|
|
|
RR R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
R |
R R |
|
|
R |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Ибо 1= i i |
= |
|
i |
|
|
= jj = |
|
j |
|
|
= kk |
|
k |
|
|
и i j |
= jk |
= ki |
= 0 так как i |
j; j |
k;k i ; |
|
|||||||||||||||||||||||||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
+ a2 b2 |
+ a3 b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Тоесть ab = a1b1 |
(24.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24.2 Доказательство формулы |
|
a |
|
= |
|
a2 + a2 |
+ a2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
Пусть a={a a a }, тогда из(24.9) имеем |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
== |
|
aa = |
a2 + a2 + a2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
a |
|
(24.10) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24.3 Вычисление угла между векторами |
|
|
|
|||||||||||||||||||||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
+ a |
|
b |
|
|
|
+ a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R |
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a b = arccos |
|
R |
R |
= arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(24.11) |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
a2 + a2 |
+ a |
|
2 |
|
|
|
b2 + b |
|
2 + b3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
1 |
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
Смотрите формулы (23.6), (24.9), (24.10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
24.4 Проекция вектора a |
|
|
на ось, коллинеарную вектору b |
|
|||||||||||||||||||||||||||||||||||||||||
Смотрите формулы (23.6), (24.9), (24.10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
R |
|
|
|
|
|
+ a2b2 |
+ a3 |
|
|
|
|
|
|
||||
ПрRa = |
aRb |
|
= |
a1b1 |
|
b3 |
, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
b |
|
|
|
|
b |
|
|
|
|
b1 + b2 |
+ b3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
a1 b1 + a2b2 + a3b3 =0 |
|
|
|
||||||||||||||||||
формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
R |
R |
|
π |
|
|
|
R R |
|
|
R |
R |
R |
|
|
R |
> 0 (либо в этом случае |
||||||
a |
b |
< |
2 |
|
a1b1 |
+ a2 b2 |
+ a3b3 |
|||||||||||||||
|
|
R |
π |
|
|
|
R |
|
|
|
R |
|
|
|
R |
|
|
|
||||
|
R |
> |
|
|
|
R |
|
R |
|
R |
|
|
< 0 |
R |
b) |
|||||||
|
a b |
|
|
|
|
a b |
|
+ a |
2 |
b |
+ a |
3 |
b |
(здесь уже cos(a |
||||||||
|
|
|
|
|
2 |
1 |
1 |
|
2 |
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(24.12) |
|
(24.13) |
далее |
R |
b) > 0 ,далее формула (23.6)) |
|
cos(a |
||
< 0 , затем используем равенство (23.6)

Вопрос №3
Расстояние между скрещивающимися прямым
L1 : |
|
x − x1 |
= |
|
y − y1 |
= |
z − z1 |
|
L || a |
1 |
|
= {α |
β |
γ |
1 |
} |
|
L |
M |
1 |
(x |
1 |
y |
z |
1 |
) |
||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
α1 |
|
β1 |
|
|
|
γ 1 |
1 |
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
L2 : |
x − x2 |
= |
|
y − y2 |
= |
z − z2 |
|
|
= {α |
|
|
|
|
} |
|
|
|
|||||||||||||||
L || a |
2 |
1 |
β |
γ |
1 |
|
L2 |
M2 (x2 y2 z2 ) |
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
α2 |
|
β2 |
|
|
|
γ 2 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 = M1 A1 и a2 = M2 A2 - направляющие векторы прямых L1 и L2 , а M1 и M2 - некоторые из их точек.
Рассмотрим параллелепипед M1C1B1 A1M2 A2C2 B2 (см. рис. 46.1). Параллельные основания которого
M1C1B1 A1 и M2 A2C2 B2 проходят через прямые L1 и L2 . Тогда расстояние между L1 и L2 ( ρ(L1, L2 ) ) - это расстояние между вышеуказанными параллельными основаниями данного параллелепипеда, т.е. его
высота ( hM |
A |
|
C ), опущенная на основание M1C1B1 A1 , равна отношению объёма данного |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параллелепипеда (VM C |
|
|
A M A C |
|
B |
) к площади основания M1C1B1 A1 ( SM C |
|
A |
), т.е. далее из §25(свойство |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
1 |
|
|
2 |
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2) при определении векторного произведения, 26, 27 (см. чему равно абсолютная величина смешанного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
произведения), 28, 24(или формулы 21.2)) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − x1 |
|
y2 − y1 |
z2 − z1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UUURUUUU |
|
|
abs |
|
α1 |
|
|
β1 |
|
γ1 |
|
|
|
|
|||||||
|
|
|
|
|
= h |
|
|
|
|
|
|
|
|
= |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
= |
(a1 a2 ,M1 M2 ) |
= |
|
|
|
α |
|
|
|
β |
|
|
|
γ |
|
|
|
|
= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M C B A M A C B |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 1 1 2 2 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M A B C |
|
|
|
|
|
|
|
|
SM C B A |
|
|
|
|
|
|
|
|
a × a |
|
|
|
β1 |
γ1 |
|
|
γ1 |
α1 |
|
α1 |
|
β1 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β2 |
γ2 |
|
|
γ2 |
α2 |
|
α2 |
|
β2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x |
|
|
-x |
|
|
y |
|
|
-y |
|
|
|
z -z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
abs |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= |
|
|
1 |
γ |
1α2 |
2 |
|
|
|
|
1 |
|
β |
21 |
2 |
+ |
|
|
|
γ1 2 |
β |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
β 2 |
2 |
|
|
|
+γ |
2 |
|
|
α 2 |
|
|
α |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
