Волновая оптика

ВОЛНОВАЯ ОПТИКА.

План лекции:

1.Когерентность и интерференция света. Условия интерференционных максимумов и минимумов. Способы наблюдения интерференции. Просветление оптики.

2.Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля.

3.Дифракция Френеля на круглом отверстии и диске.

4.Дифракция Фраунгофера на одной щели и дифракционной решетке

5.Дифракционная решетка. Дифракция на пространственной решетке.

6.Естественный и поляризованный свет. Виды поляризации. Поляризаторы и

анализаторы. Закон Малюса. Степень поляризации.

7. Поляризация при отражении и преломлении света. Угол Брюстера и закон Брюстера. Вращение плоскости поляризации и сахариметрия. Двойное лучепреломление.

1.Когерентность и интерференция света. Условия интерференционных максимумов и минимумов. Время и длина когерентности. Способы наблюдения интерференции. Просветление оптики.

Вволновой оптике рассматриваются такие оптические явления, как интерференция, дифракция и поляризация, в которых проявляется волновая природа света. Волновая теория света основывается на принципе Гюйгенса (1678): каждая точка, до которой доходит волна, служит источником вторичных сферических волн,

аогибающая этих волн дает положение волнового фронта в следующий момент времени.

Принцип Гюйгенса объясняет распространение световых волн, описываемое законами геометрической оптики.

Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.

Степень согласованности называют степенью когерентности, чем лучше согласованность, тем выше степень когерентности.

1

Два колебательных или волновых процесса называют некогерентными, когда они не согласованы друг с другом.

Монохроматические волны ‒ неограниченные в пространстве волны одной фиксированной частоты и постоянной амплитуды - когерентны.

Интерференция света ‒ это сложение в пространстве двух или нескольких когерентных световых волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны.

Пусть в некоторую точку пространства М приходят от разных источников две монохроматические световые волны с циклической частотой со и с одинаковым направлением колебаний световых векторов 1 и 2. Согласно принципу суперпозиции образуется результирующая гармоническая волна

интенсивность световой волны пропорциональна квадрату амплитуды светового вектора, т. е. ~2.

В случае некогерентных волн разность фаз изменяется во времени слу-

чайным образом. Поэтому среднее по времени значение cos = 0 и интенсивность результирующего колебания в любой точке пространства равна сумме

интерференция в этом случае отсутствует.

В случае суперпозиции когерентных волн разность фаз постоянна во времени и интенсивность результирующего колебания определяется как

2

где 1 и 2 – геометрические длины путей первой и второй волны, которые соответственно распространяются в средах с показателями преломления 1 и 2.

Таким образом, при сложении когерентных волн результирующая интенсивность в одних точках пространства будет больше суммы интенсивностей взаимодейст-

вующих волн (интерференционные максимумы), в других ‒ меньше суммы ин-

тенсивностей взаимодействующих волн (интерференционные минимумы).

Условие интерференционного максимума:

если оптическая разность хода волн равна четному числу полуволн в ва-

кууме (целому числу длин волн), то колебания, возбуждаемые обеими волнами в точке , будут происходить в фазе

где – целое число (порядок интерференции). В точках пространства, в кото-

рых наблюдаются интерференционные максимумы, разность фаз когерентных волн равна четному числу :

Условие интерференционного минимума:

если оптическая разность хода волн ∆ равна нечетному числу полуволн в ва-

кууме, то образуются интерференционные минимумы

При этом разность фаз когерентных волн равна нечётному числу :

Реальные источники не дают строго монохроматического света. В неза-

висимых источниках свет излучается атомами, каждый из которых испускает свет лишь в течение ~10−8с. Только в течение этого времени волны, испускаемые атомом, имеют постоянные амплитуду и фазу колебаний. Независимые когерентные источники возможно получить, используя лазеры.

Немонохроматический свет можно представить в виде совокупности сменяющих друг друга коротких гармонических импульсов излучаемых атомами ‒ волновых цугов.

В качестве количественной меры степени когерентности световых колебаний,

не зависящей от способа измерения интерференционной картины используются следующие величины:

1)временя когерентности ‒ средняя продолжительность одного волнового цуга ког. Если при наложении волновых полей временной сдвиг между ними мал по сравнению с ког, то может быть получена четкая интерференционная картина. Иначе при ког интерференционная картина наблюдаться не будет. Величина ког также ограничивает время измерения интерференционной картины.

2)Длина когерентности (длина цуга) – это расстояние, на которое пере-

мещается волна за время когерентности. В вакууме длина когерентности равна

4

3)Длине когерентности соответствует максимально возможный порядок интерференции , начиная с которого полосы исчезают:

где – длина волны; ∆ – ширина спектрального интервала интерферирующе-

го света. Величина ⁄∆ характеризует степень монохроматичности света.

Общий принцип получения когерентных световых волн таков: волну, из-

лучаемую одним источником света, разделяют некоторым способом на две части,

которые достигают точки наблюдения по разным путям. В результате между ними возникает разность хода.

Методы наблюдения интерференции:

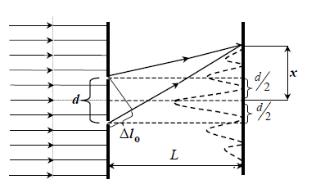
1. Метод Юнга. Непрозрачный экран с двумя щелями, равноудалёнными от оси на расстояние d/2, освещают монохроматической плоской световой волной,

исходящей от удалённого источника. Согласно принципу Гюйгенса-Френеля щели,

будучи расположенными на одном волновом фронте, сами являются источниками когерентных световых волн, которые могут интерферировать. В результате интерференции волн, исходящих от щелей, на втором экране, расположенном параллельно первому на расстоянии L, можно наблюдать чередующиеся тёмные и светлые полосы (совокупность этих полос называют интерференционной картиной).

Рисунок 2 ‒ Метод Юнга

5

В случае, если источник света немонохроматический, то интерференционная картина представляет собой набор чередующихся окрашенных полос.

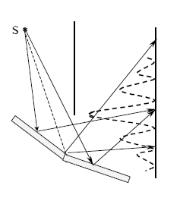
2. Метод Френеля. Свет от источника S падает расходящимся пучком на два плоских зеркала, распложенных относительно друг друга под углом, немного меньшим 180о. Лучи, отражённые зеркалами, взаимно когерентны и поэтому могут интерферировать. Интерференционную картину наблюдают на экране, расстояние от которого до разных точек зеркал, различно, что и обусловливает постепенное изменение оптической разности хода между интерферирующими лучами.

Рисунок 3 ‒ Метод Френеля

3. Интерференция света в тонких плёнках (метод Ньютона). В природе часто можно наблюдать радужное окрашивание тонких плёнок (масляные плёнки на воде, мыльные пузыри, крылышки насекомых, оксидные плёнки на металлах и т.п.),

возникающее в результате интерференции света, отражённого двумя поверхностями плёнки. Падающий на пластинку пучок, отражаясь от её обеих поверхностей,

расщепляется на два когерентных пучка, которые и интерферируют в отражённом свете.

4. Метод Ллойда заключается в получении мнимого изображения источника света с помощью специального однослойного зеркала.

Просветление оптики. Объективы оптических приборов содержат большое количество линз. Даже незначительное отражение света каждой из поверхностей

6

линз (около 4 % падающего света) приводит к тому, что интенсивность прошедшего пучка света значительно уменьшается. Кроме того, в объективах возникают блики и фон рассеянного света, что снижает эффективность оптических систем. В

призменном бинокле, например, суммарная потеря светового потока достигает

~50%. Но на границах сред можно создать такие условия, когда интенсивность света, прошедшего через оптическую систему, будет максимальна.

Отметим, что обычно просветление оптики выполняют для средней (желто-

зеленой) области видимого спектра. Как следствие, в отраженном свете объективы кажутся пурпурными из-за смешения красного и фиолетового цветов. Современные технологии синтеза оксидных пленок (например золь-гель- методом) позволяют создавать на основе элементов структуры металл-оксид-полупроводник новые просветляющие, защитные покрытия в оптоэлектронике.

При интерференции многих волн яркость интерференционной картины является периодической, но не гармонической функцией оптической разности хода интерферирующих лучей. Благодаря этому многолучевая интерференция получила важные практические применения в спектроскопии, метрологии. Например, для спектрального анализа света широко применяется явление резкой зависимости яркости интерференционной картины от δ.

Явление интерференции широко применяется в оптической технике и производстве: контролируется качество линзовых систем, создаются светофильтры,

высококачественные зеркала, просветляющие покрытия для оптических деталей. В

рефрактометрии с целью определения показателей преломления жидких, твердых или газообразных веществ интерференция света используется для точного измерения расстояний и углов. С помощью рефрактометров в физической химии устанавливают состав и структуру веществ, в фармацевтической промышленности контролируют состав и качество продуктов.

2. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля

7

Дифракцией света называется огибание светом препятствий, встречающихся на его пути, или в более широком смысле ‒ любое отклонение распространения света от законов геометрической оптики. В результате дифракции свет проникает в область геометрической тени. Распределение интенсивности света на экране,

получаемое вследствие дифракции, называется дифракционной картиной.

Принцип Гюйгенса не объясняет явления дифракции. Французский физик О.

Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции (1815). Это позволило рассматривать дифракционные явления на основе принципа Гюйгенса-Френеля. Приближенность решений задач с помощью данного принципа состоит в том, что при этом не рассматриваются реальные граничные условия электродинамики Максвелла.

Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции

(сложения) когерентных вторичных волн, излучаемых вторичными (фиктивными)

источниками - бесконечно малыми элементами любой замкнутой волновой поверхности, охватывающей источник S. В рамках волновой теории с помощью этого принципа описывают и объясняют механизм распространения электромагнитных волн, в частности световых.

Рассмотрим в произвольной точке амплитуду световой волны,

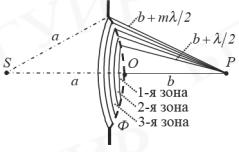
распространяющейся в однородной среде из точечного источника . Обозначим через расстояние от вершины волновой поверхности до точки , рис. 1.

Рисунок 1‒ Зоны Френеля

8

Согласно принципуГюйгенса-Френеля заменим действие источника дей-

ствием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из

(поверхность сферы с центром и радиусом ).

Разобьем волновую поверхность Ф на зоны Френеля - кольцевые зоны такого размера, чтобы колебания, возбуждаемые двумя соседними зонами в точке ,

происходили в противофазе. Тогда расстояния от краев зоны до должны отличаться на ⁄2, где – длина волны в той среде, в которой распространяется волна.

Тогда, обозначив амплитуды колебаний от 1-й, 2-й, ... -й зон Френеля через 1, 2, … , (при этом 1 > 2 > 3 >. ..), получим амплитуду результи-

рующего колебания: = 1 − 2 + 3 − 4+. ..

При таком разбиении волновой поверхности на зоны оказывается, что амплитуда колебания от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон: = (−1 + +1)/2.

Учтем, что при 1 1 . Можно показать, что результирующая амплитуда в точке будет равна

= √ +

При = = 10см и = 500нм радиус первой зоны 1 = 0,158мм.

3. Дифракция Френеля на круглом отверстии и диске

9

Дифракция Френеля (дифракция в сходящихся лучах) – это дифракция,

осуществляемая в случае, когда на препятствие падает сферическая волна, а дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, и

представляет собой «дифракционное изображение» препятствия.

Дифракция на круглом отверстии.

Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути препятствие с круглым отверстием . Дифракционная картина наблюдается на экране Э, параллельном плоскости отверстия и находящемся от него на расстоянии , рис. 2, а.

Амплитуда света в точке экрана Э будет равна

где знак «плюс» берется для случая, когда отверстие открывает нечетное

число зон Френеля, а знак «минус» – для четного .

Дифракционная картина будет иметь вид чередующихся темных и светлых колец с центром в точке (если нечетное, то центральное кольцо будет светлым

(рис. 2, б), если четное, то - темным (рис. 2, в)).

Шириной дифракционного максимума на экране называется расстояние между двумя ограничивающими его дифракционными минимумами.

Если диаметр отверстия велик, так что 1⁄2, то дифракционной кар-

тины на экране не будет.

Дифракция на диске. Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути диск диаметром , рис.3, а. Диск закрывает первые т зон Френеля. Амплитуда колебания в точке равна

10