КМ МО-317 Ибрагимова. ЛР2

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ИНФОРМАТИКИ И РОБОТОТЕХНИКИ

КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И КИБЕРНЕТИКИ

		УТВЕРЖДАЮ Проректор университета по научной работе ФИО
		"___" ______________ _______г.
Лабораторная работа № 2 «Генерирование случайных процессов»
по предмету: КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Преподаватель			А. Ф. Валеева
Исполнитель			К.Б. Ибрагимова
Уфа - 2021

ЗАДАНИЕ

Реализовать два алгоритма генерации случайных процессов: пуассоновский однородный и пуассоновский неоднородный. Проверить каждый на основе полученных данные по критерию согласия К. Пирсона принадлежность исследуемой случайной переменной пуассоновскому закону распределения.

Ход работы

1. Реализуем генерирование однородного пуассоновского процесса

Входные данные:

T – время окончания процесса

λ – значение интенсивности

Выходные данные:

S – массив значений времен событий процесса в возрастающем порядке

I – число событий, которые произойдут к моменту времени T

Алгоритм

1. Вводим входные данные.

2. Инициализируем значение начального времени t.

3. Инициализируем массив S значений времен событий процесса.

4. Генерируем случайное число u на отрезке [0,1].

5. Задаем значение начального времени t по формуле:

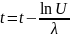
6. Если t > T, то:

   1. Заносим t в массив S значений времен событий процесса.

7. Иначе возвращаемся к шагу 4.

8. Считаем число событий, которые произойдут к моменту времени T.

2. Реализуем генерирование неоднородного пуассоновского процесса

Входные данные:

T – время окончания процесса

λ – значение интенсивности

Промежуточные данные:

λ(t) – функция интенсивности

Выходные данные:

S – массив значений времен событий процесса в возрастающем порядке

I – число событий, которые произойдут к моменту времени T

Алгоритм

1. Вводим входные данные.

2. Инициализируем значение начального времени T.

3. Инициализируем массив S значений времен событий процесса.

4. Генерируем случайное число U на отрезке [0,1].

5. Задаем значение начального времени t по формуле:

6. Если t > T, то:

   1. Генерируем случайное число U2 на отрезке [0,1].

   2. Если :

      1. Заносим t в массив S значений времен событий процесса.

7. Иначе возвращаемся к шагу 4.

8. Считаем число событий, которые произойдут к моменту времени T.

3. Далее реализуем проверку по критерию 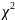число событий в интервале времени заданного пуассоновского процесса пуассоновскому распределению

Входные данные:

T – время окончания процесса

λ – значение интенсивности

N – количество испытаний

Промежуточные данные:

λ(t) – функция интенсивности

Выходные данные:

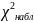– подсчитанное значение критерия согласия Пирсона

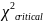– критическое значение критерия согласия Пирсона при α = 0,05.

Алгоритм проверки:

1. Получим входные данные

2. Инициализируем массив frequencies частот числа событий в интервале времени:

3. Считаем частоты числа событий на интервале времени длины T.

4. Вычисляем число групп выборки s.

5. Находим выборочное среднее mean.

6. Зададим оценку параметра значением выборочного среднего.

7. Инициализируем массив theoryFrequencies теоретических частот числа событий в интервале времени.

8. Вычисляем теоретические частоты числа событий в интервале времени по формуле:

9. Вычисляем по формуле:

10. Сравним и табличное значение при α = 0.05 и степенью свободы k = s – 2.

11. Если , то гипотеза о принадлежности числа событий на интервале времени длины T заданного пуассоновского процесса пуассоновскому распределению принимается.

12. Иначе не принимается.

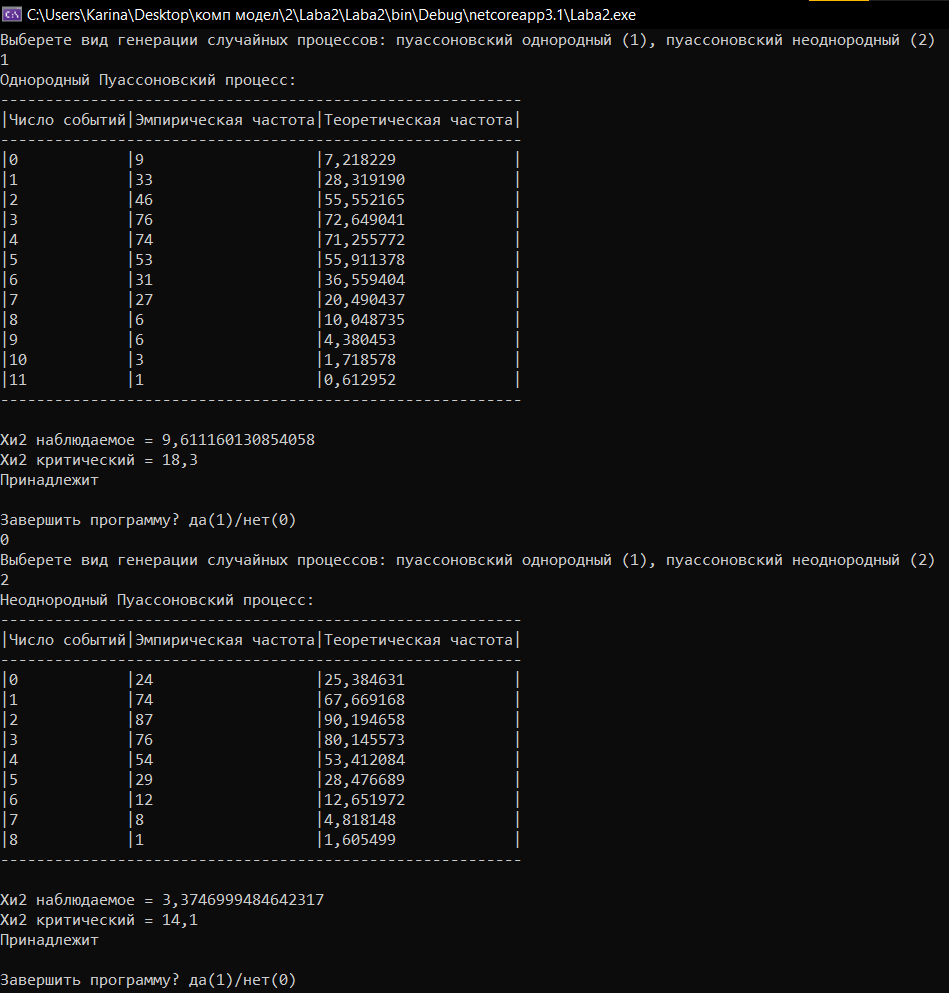
результат работы программы

ЛИСТИНГ ПРОГРАММЫ

using System;

using System.Collections.Generic;

using System.Linq;

namespace KM_2

{

class Program

{

static double FunctionIntensity(double t)

{

return 1 + (1 / (t + 2));

}

static List<double> PoissonProcessUniform(int T, double lambda)

{

Random rnd = new Random();

//текущее время

double t = 0;

List<double> S = new List<double>();

double U = rnd.NextDouble();

t = t - (Math.Log(U) / lambda);

while (!(t > T))

{

S.Add(t);

U = rnd.NextDouble();

t = t - (Math.Log(U) / lambda);

}

return S;

}

static List<double> PoissonProcessNonuniform(int T, double lambda)

{

var rnd = new Random();

double t = 0;

var S = new List<double>();

double U = rnd.NextDouble();

t = t - (Math.Log(U) / lambda);

while (!(t > T))

{

double U2 = rnd.NextDouble();

var p = FunctionIntensity(t) / lambda;

if (U2 <= p)

{

S.Add(t);

}

U = rnd.NextDouble();

t = t - (Math.Log(U) / lambda);

}

return S;

}

static double Factorial(int x)

{

if (x < 2)

return 1;

var result = 1;

for (var i = 1; i <= x; i++)

{

result *= i;

}

return result;

}

static void CheckPoisson(List<int> frequencies, int experiments)

{

var chi2Criticals = new double[] {

3.8, 6, 7.8, 9.5, 11.1, 12.6, 14.1, 15.5, 16.9, 18.3,

19.7,21,22.4,23.7,25,26.3,27.6,28.9,30.1,31.4

};

// величина разбития

var s = frequencies.Count;

// считаем выборочное среднее

double mean = 0;

for (int i = 0; i < s; i++)

{

mean += frequencies[i] * i;

}

mean /= experiments;

// оценочная интенсивность

var lambdaTheory = mean;

// теоретические частоты

var theoryFrequencies = new List<double>();

for (int i = 0; i < s; i++)

{

var pi = Math.Exp(-lambdaTheory) * Math.Pow(lambdaTheory, i) / Factorial(i);

theoryFrequencies.Add(pi * experiments);

}

// хи квадрат

double chi2 = 0;

for (int i = 0; i < s; i++)

{

chi2 += Math.Pow(frequencies[i] - theoryFrequencies[i], 2) / theoryFrequencies[i];

}

// степени свободы

var k = s - 2;

// вывод таблицы

Console.WriteLine("----------------------------------------------------------");

Console.WriteLine(String.Format("|{0,13}|{1,20}|{2,21}|", "Число событий", "Эмпирическая частота", "Теоретическая частота"));

Console.WriteLine("----------------------------------------------------------");

for (int i = 0; i < s; i++)

{

Console.WriteLine(String.Format("|{0,-13}|{1,-20}|{2,-21:f6}|", i, frequencies[i], theoryFrequencies[i]));

}

Console.WriteLine("----------------------------------------------------------");

Console.WriteLine();

Console.WriteLine($"Хи2 наблюдаемое = {chi2}");

Console.WriteLine($"Хи2 критический = {chi2Criticals[k - 1]}");

Console.WriteLine(chi2 <= chi2Criticals[k - 1] ? "Принадлежит" : "Не принадлежит");

}

static void Main(string[] args)

{

int exit = 0;

do

{

//Console.Write("Введите момент времени T = ");

//int T = int.Parse(Console.ReadLine());

//Console.Write("Введите параметр интенсивности lambda = ");

//double lambda = double.Parse(Console.ReadLine());

//Console.Write("Введите количество испытаний N = ");

//int N = int.Parse(Console.ReadLine());

int T = 2; double lambda = 2; int experiments = 365;

Console.WriteLine("Выберете вид генерации случайных процессов: пуассоновский однородный (1), пуассоновский неоднородный (2)");

int flag = int.Parse(Console.ReadLine());

switch (flag)

{

case 1:

Console.WriteLine("Однородный Пуассоновский процесс:");

var frequencies1 = new List<int>();

for (int i = 0; i < experiments; i++)

{

var I = PoissonProcessUniform(T, lambda).Count;

//дозаполняем массив нулями

if (frequencies1.Count <= I)

{

frequencies1.AddRange(Enumerable.Repeat(0, I - (frequencies1.Count - 1)));

}

frequencies1[I] += 1;

}

CheckPoisson(frequencies1, experiments);

Console.WriteLine();

Console.WriteLine("Завершить программу? да(1)/нет(0)");

exit = int.Parse(Console.ReadLine());

break;

case 2:

Console.WriteLine("Неоднородный Пуассоновский процесс:");

var frequencies2 = new List<int>();

for (int i = 0; i < experiments; i++)

{

var I = PoissonProcessNonuniform(T, lambda).Count;

if (frequencies2.Count <= I)

{

// дозаполняем массив нулями

frequencies2.AddRange(Enumerable.Repeat(0, I - (frequencies2.Count - 1)));

}

frequencies2[I] += 1;

}

CheckPoisson(frequencies2, experiments);

Console.WriteLine();

Console.WriteLine("Завершить программу? да(1)/нет(0)");

exit = int.Parse(Console.ReadLine());

break;

default:

Console.WriteLine("Default case");

break;

}

} while (exit == 0);

}

}

}

Вывод

В ходе лабораторной работы были получены навыки генерации однородных и неоднородных пуассоновских процессов. Также были получены навыки проверки по критерию согласия принадлежность числа событий на интервале времени пуассоновского процесса пуассоновскому закону распределения.