10. Отношения между понятиями.

Равнозначности (тождества) - Каждый круг охватывает объем понятия, а сами понятия символически обозначаются буквами. Так, приведенный пример равнозначности понятий графически выглядит следующим образом:

Пересечение (перекрещивание) — такое отношение, которое характеризует частичное совпадение объемов понятий, но при этом ни одно из них не входит полностью в объем другого.

Подчинение (субординация) — такое отношение, когда объем одного понятия полностью входит в объем другого. При этом более широкое по объему понятие является подчиняющим (родовым), а менее широкое по объему — подчиненным (видовым). Родовидовые отношения лежат в основе многих логических операций с понятиями (обобщение, ограничение, определение и деление).

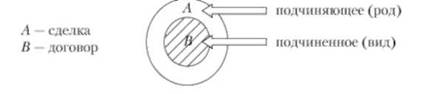
• Несовместимые понятия имеют также три вида отношений.

Соподчинение (координация) — такое отношение, которое свидетельствует, что в родовое понятие входит не одно, а два или более однопорядковых видовых понятий.

Противоположность (контрарность) — такое отношение, в котором находятся понятия, одно из которых содержит некоторые признаки, а другое эти признаки отрицает, замещая их исключающими признаками. Другими словами, объемы противоположных понятий разделены объемом некоторого третьего понятия. Слова, выражающие противоположные понятия, называются антонимами ("черный" — "белый"). Сумма объемов противоположных понятий не исчерпывает объема родового понятия. Между понятиями "черный" и "белый" может быть понятие, отражающее любой другой цвет: зеленый, красный и т.д.

Противоречие (контрадикторность) — такое отношение, в котором находятся понятия, одно из которых содержит некоторые признаки, а другое отрицает эти же признаки, не замещая их никакими другими признаками. Объемы двух противоречащих понятий составляют в сумме весь объем рода, видами которого они являются.

Знание разновидностей понятий, а также отношений между ними служит основой для уяснения операций с понятиями, для изучения других форм мышления

11. Определение понятий и виды определений. Приемы, сходные с определением.

Определение – это логическая операция, раскрывающая основное содержание понятия путем перечисления входящих в него признаков.

Цель определения – отличить предмет, отражаемый понятием, от сходных с ним предметов, установить точное значение слова или выражения. Приведем пример: Студент – учащийся высшего учебного заведения. «Студент» – определяемое понятие, а «учащийся высшего учебного заведения» – определяющее понятие.

Классификация:

реальные и номинальные (по цели)

1) Реальные определения относятся к самому предмету и отвечают на вопрос: что этот предмет из себя представляет? Реальное определение опирается на существенные признаки самого предмета.

Например: «Улика – доказательство виновности обвиняемого в совершенном преступлении».

2) Номинальные определения относятся к имени предмета. Они отвечают на вопрос: что обозначает тот или иной термин? С помощью номинальных определений вводятся новые понятия, задается смысл новых терминов, приводится истолкование, интерпретация уже известных терминов.

явные и неявные (по способу раскрытия содержания понятия)

1) Явными называются определения, в которых указываются признаки, присущие определенному предмету. Такие определения имеют форму равенства:

Наиболее распространенным способом явного определения является определение через ближайший род и видовое отличие.

Например: Виктор Гюго – французский писатель (род), написавший роман «Отверженные» (видовое отличие).

Еще один вид явного определения – генетическое определение – определение, в котором видовым признаком является способ происхождения, создания, конструирования предмета.

Пример: «Окружность есть замкнутая линия, образованная вращением радиуса определенной длины вокруг неподвижной точки в некоторой плоскости».

Операциональное определение – вид явного определения, в котором видовым признаком является указание на операцию, помогающую распознать те или иные предметы.

Пример: «Кислота – это жидкость, окрашивающая лакмусовую бумажку в красный цвет».

2) Неявные определения. В неявных определениях выявляются отношения, в которых находится определяемый предмет с другими предметами в определенном контексте.

К числу неявных относятся:

• аксиоматические определения, используемые в математике. В таких определениях термин определяется путем указания той совокупности аксиом, в которой он содержится. Так как аксиомы – это истинные суждения о предметах некоторой предметной области, то термин, входящий в эти аксиомы, получает свое значение. Так, в геометрии Евклида неявно определяются такие понятия, как «точка», «прямая», «плоскость».

• индуктивные определения – также всем хорошо известны из математики. Примером такого определения является определение натурального числа.

• контекстуальные определения - определение в котором некоторый контекст использования определяемого понятия приравнивается к другому контексту, не включающему определяемое понятие. Мы используем контекстуальные определения, например, во время беседы, – если встречается незнакомое слово, то мы пытаемся понять его значение, исходя из контекста беседы.

Приемы, сходные с определением

Кроме определений, существуют также широко распространенные операции, сходные с определением (но определением не являющиеся), такие как: описание, характеристика, сравнение, различение и так называемое «остенсивное определение».

Задача описания состоит в том, чтобы наиболее точно и полно указать признаки предмета (события, места, где оно произошло, лица и т. д.).

Описание играет важную роль в следственной практике, например, при осмотре места преступления. Следователь, составляющий протокол осмотра, должен стремиться к наиболее полному описанию, фиксируя не только то, что явно связано с событием, но и то, что может быть, а может и не быть с ним связано.

Характеристика состоит в указании отличительных, характерных признаков конкретного предмета, человека, события. К характеристике часто прибегают в судебных речах, например, характеризуя личность обвиняемого или жертвы.

Сравнение может рассматриваться как художественный прием, заключающийся в том, что один предмет сравнивается с другим, сходным с ним в определенном отношении. Этот прием применяется для образной характеристики предмета.

Приведем примеры: «Юрист, который изучает логику, но не применяет ее, подобен крестьянину, который пашет, но не сеет» (народная мудрость).

Остенсивное определение – определение путем прямого указания на предмет, входящий в объем данного понятия. Остенсивные определения сопровождают нас на протяжении всей нашей жизни. Ребенка обучают языку, показывая ему на предметы: «Смотри, это птичка!».