Лабораторная работа № 3 законы ома и кирхгофа для цепи постоянного тока

Запустите программу. Выберите «Электричество и магнетизм» и «Цепи постоянного тока». Нажмите вверху внутреннего окна кнопку с изображением страницы.

Цель работы:

знакомство с компьютерным моделированием цепей постоян-ного тока;

экспериментальное подтверждение законов Ома и Кирхгофа.

Краткие сведения из теории

Силы тока, по определению, это заряд, перенесённый за едини-цу времени, т.е.:

I ^dq_dt .

Закон Ома для участка цепи: величина (сила) тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике:

I _R¹ U ,

где R – сопротивление проводника.

Резистором называется устройство, обладающее заданным по-стоянным сопротивлением.

Напряжение на резисторе U _R IR .

18

Закон Ома для неоднородного участка цепи:

_I 1 2 ^E12 _,

R

где ₁ и ₂ – потенциалы концов участка;

E₁₂ – ЭДС, действующая на данном участке цепи.

Закон Ома для замкнутой цепи:

I ^E_R ,

где E – суммарная ЭДС, действующая в цепи;

R – суммарное сопротивление всей цепи.

Разветвлённой цепью называется электрическая цепь, имеющая узлы. Узлом называется точка, в которой сходится более чем два про-водника. Ток, текущий к узлу, принято считать положительным, а ток, текущий от узла, – отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходя-щихся в узле, равна нулю I_k 0 .

Второе правило Кирхгофа: в каждом из замкнутых контуров, которые можно мысленно выделить в данной разветвлённой цепи, ал-гебраическая сумма падений напряжения равна алгебраической сумме ЭДС:

Ik Rk Ek .

При анализе разветвлённой цепи следует обозначать с одним индексом ток, протекающий по всем последовательно соединённым элементам от одного узла до другого. Направление каждого тока вы-бирается произвольно.

При составлении уравнений второго правила Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным (как вам удобно) направлением обхода:

1. Ток принято считать положительным, если он совпадает с на-правлением обхода, и отрицательным, если он направлен против это-го направления;

2. ЭДС считается положительной, если её действие (создавае-мый ею ток) совпадает с направлением обхода.

Количество уравнений первого правила Кирхгофа должно быть на одно меньше количества узлов в данной цепи. Количество незави-симых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные кон-туры.

19

Методика и порядок измерений

В данной лабораторной работе исследуется модель простейшей разветвлённой электрической цепи, состоящей из трёх источников ЭДС, подключённых параллельно к одному резистору (нагрузке).

Внимательно рассмотрите рисунок 3.1, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.

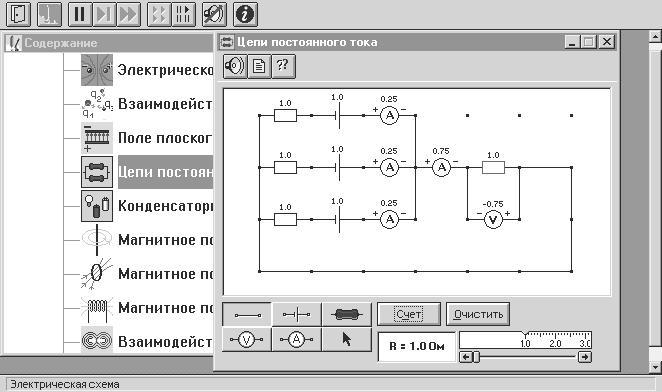
Рис. 3.1. Разветвлённая электрическая цепь

Нарисуйте в конспекте эквивалентную схему цепи, распологая источники один под другим и учитывая наличие внутреннего сопро-тивления у каждого источника. Укажите знаки ЭДС, направления то-ков в каждом участке и направления обхода каждого замкнутого кон-тура. Составьте систему уравнений для нахождения токов в каждом участке.

Соберите на экране заданную эквивалентную цепь. Для этого сначала щёлкните левой кнопкой мыши над кнопкой ЭДС в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Ориентируйтесь на рисунок схемы.

Щёлкните левой кнопкой мыши в рабочей части экрана, где бу-дет расположен первый источник ЭДС. Переместите маркер мыши вниз на одну клетку и снова щёлкните левой кнопкой под тем местом, где расположился первый источник. Там появится второй источник ЭДС. Аналогично разместите и третий источник.

Разместите далее последовательно с каждым источником рези-стор, изображающий его внутреннее сопротивление (нажав предвари-тельно кнопку R в нижней части экрана) и амперметр (кнопка А там же).

20

Затем расположите резистор нагрузки и последовательно соединён-ный с ним амперметр. Под нагрузкой расположите вольтметр, изме-ряющий напряжение на нагрузке.

Подключите соединительные провода. Для этого нажмите кноп-ку провода внизу экрана, после чего переместите маркер мыши в ра-бочую зону схемы. Щёлкните левой кнопкой мыши в точке, где про-ходит провод.

Установите значения параметров для каждого элемента. Для этого щёлкните левой кнопкой мыши на кнопке со стрелкой. Затем щёлкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удер-живая её в нажатом состоянии, меняйте величину параметра и уста-новите числовое значение, равное взятому из таблицы 3.1, для вашей бригады.

Таблица 3.1

Значения ЭДС и внутреннего сопротивления источников (не перерисовывать)

Бригада	1	2	3	4	5	6	7	8
E1 , E2 , E3 , В	3,7,-2	4,-3,-8	3,6,-4	6,-2,-8	-6,5,8	5,8,-4	-4,6,-7	8,-4,6
R1 , R2 , R3 ,Ом	2,1,1	1,3,1	2,1,2	1,1,2	2,1,1	1,2,1	1,1,2	1,3,1

Установите сопротивления резистора нагрузки R 1 Ом. Измерь-те значения всех токов и напряжения на нагрузке (щёлкнув мышью по кнопке «Счёт») и запишите их в таблицу 3.2. Меняя сопротивление R , повторите измерения параметров и заполните таблицу 3.2.

Таблица 3.2

Результаты измерений

R, Ом	I1 , A	I2 , A	I3 , A	I , A	U , В
1
2
3
4
5
6

21

Обработка данных и анализ результатов

1. Запишите для вашей цепи решение системы уравнений для всех токов в общем виде.

2. Рассчитайте значения всех токов для каждого сопротивления нагрузки и запишите в таблицу 3.3.

	Результаты расчёта		Таблица 3.3
I1 , A	I2 , A	I3 , A	I, A

3. Постройте график экспериментальной зависимости падения напряжения U от тока I на нагрузке.

4. Сформулируйте выводы по графику.

Контрольные вопросы

1. Что такое электрический ток?

2. Дайте определение величины (силы) тока.

3. Дайте определение разности потенциалов (напряжения).

4. Напишите формулу, связывающую приращение потенциалов и напряжение.

5. Что такое резистор?

6. Напишите формулу для сопротивления последовательно со-единённых резисторов.

7. Напишите формулу для сопротивления параллельно соеди-нённых резисторов.

8. Напишите закон Ома для участка цепи. Сравните его с зако-ном Ома в дифференциальной (локальной) форме.

9. Какой участок цепи называется неоднородным?

22

10. Запишите закон Ома для неоднородного участка цепи.

10. Какими характеристиками описывается источник ЭДС?

10. Сформулируйте первый закон Кирхгофа. Какое свойство за-ряда он отражает?

11. Запишите формулу для первого закона Кирхгофа.

10. Сформулируйте второй закон Кирхгофа.

10. Запишите формулу для второго закона Кирхгофа.

10. Что такое узел электрической цепи?

10. Что такое полная электрическая цепь?

Лабораторная работа № 4 МАГНИТНОЕ ПОЛЕ ПРОВОДНИКА И ВИТКА С ТОКОМ

Запустите программу. Выберите «Электричество и магнетизм» и «Магнитное поле прямого тока». Нажмите вверху внутреннего окна кнопку с изображением страницы.

Цель работы:

знакомство с моделированием магнитного поля от различных источников;

экспериментальное подтверждение закономерностей для маг-нитного поля прямого провода и кругового витка (контура) с током;

экспериментальное определение величины магнитной посто-янной.

Краткие сведения из теории

Магнитным полем называется то, что существует в области про-странства, в которой на электрически нейтральный проводник с током действует сила, называемая магнитной. Источником магнитного поля является движущаяся электрически заряженная частица (заряд), кото-рая создаёт также и электрическое поле.

Если вблизи одной движущейся заряженной частицы (заряда № 1) будет находиться вторая движущаяся с такой же скоростью V заря-женная частица (заряд № 2), то на второй заряд будут действовать

23

две силы: электрическая (кулоновская)	FЭЛ и магнитная сила
			FМ , ко-
V		2
торая будет меньше электрической в		раз, где c – скорость света
	c

в вакууме.

Практически для любых проводов с током выполняется принцип квазинейтральности. Несмотря на наличие и движение заряженных частиц внутри проводника, любой (не слишком малый) его отрезок имеет нулевой суммарный электрический заряд. Поэтому между обычными проводами с током наблюдается только магнитное взаи-модействие.

Магнитная индукция – характеристика силового действия маг-

нитного поля на проводник с током, векторная величина, обозначае-

мая символом B .

Линии магнитной индукции – линии, в любой точке которых вектор индукции магнитного поля направлен по касательной.

Анализ взаимодействия движущихся зарядов с учётом эффектов

теории относительности (релятивизма) даёт выражение для индук-

ции dB магнитного поля, создаваемого элементарным отрезком dL c током I , расположенным в начале координат (закон Био – Савара –

Лапласа):

dB ₄ ⁰_r^I₂ dL, e_r ,

где r – радиус-вектор точки наблюдения;

e_r – единичный радиус-вектор, направленный в точку наблюде-

ния; ₀ – магнитная постоянная.

Магнитное поле подчиняется принципу суперпозиции: индук-ция магнитного поля нескольких источников является суммой индук-ций полей, создаваемых независимо каждым источником:

BСУМ Bi . i

Циркуляцией магнитного поля называется интеграл по некото-рому контуру от скалярного произведения индукции магнитного поля на элемент контура:

Г_B BdL .

L

24

Закон циркуляции магнитного поля: циркуляция магнитного по-ля по замкнутому контуру L₀ пропорциональна суммарному току,

пронизывающему поверхность S(L₀ ) , ограниченную этим контуром L₀ :

Г0B BdL 0 I j .

L₀ j

Закон Био – Савара – Лапласа и принцип суперпозиции магнит-ного поля позволяют получить многие другие закономерности, в ча-стности индукцию магнитного поля прямого бесконечно длинного проводника с током:

2. 0 ^I _.

2 r

Линии магнитной индукции поля прямого проводника с током представляют собой концентрические окружности, лежащие в плос-костях, перпендикулярных проводнику, с центрами, расположенными на его оси.

Индукция магнитного поля на оси кругового контура (витка) ра-

диуса R с током I на расстоянии r			от центра:
	0		pm	,
B	2
		(R2 r 2 )3 / 2

где p_m ISe_n – магнитный момент витка площадью S ; e_n – единичный вектор нормали к поверхности витка.

Соленоидом называется длинная прямая катушка с током. Вели-чина индукции магнитного поля вблизи центра соленоида меняется очень мало. Такое поле можно считать практически однородным.

Из закона циркуляции магнитного поля можно получить форму-лу для индукции магнитного поля в центре соленоида:

B ₀ In ,

где n – число витков, приходящихся на единицу длины соленоида.

Методика и порядок измерений

Рассмотрите внимательно рисунки 4.1–4.3, изображающие ком-пьютерные модели. Найдите на них все основные регуляторы и поле эксперимента. Зарисуйте необходимое в конспект.

25

Рис. 4.1. Магнитное поле прямого тока

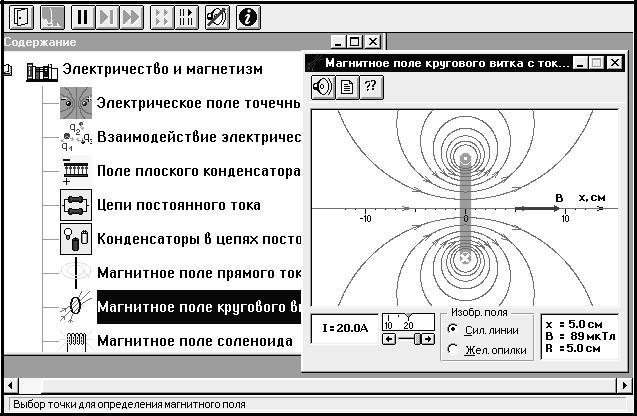
Рис. 4.2. Магнитное поле кругового тока

26

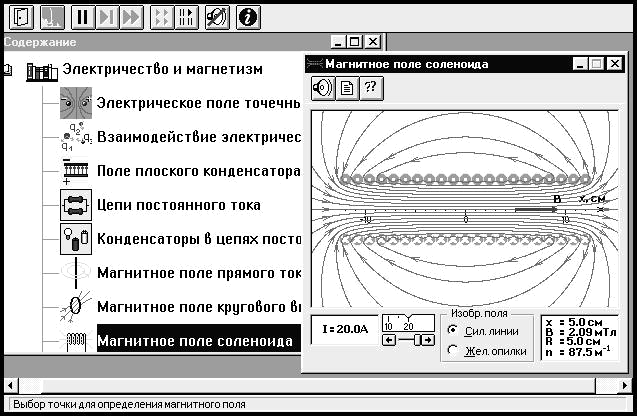
Рис. 4.3. Магнитное поле соленоида

Эксперимент 1

1. Запустите, дважды щёлкнув мышью, эксперимент «Магнит-ное поле прямого тока». Наблюдайте линии индукции магнитного по-ля прямого провода.

2. Зацепив мышью, перемещайте движок регулятора тока. За-фиксируйте величину тока, указанную в таблице 4.1, для вашей бри-гады.

				Таблица 4.1
Значения величины тока (не перерисовывать)
Бригады	I1	I2	I3		I4
1 и 5	5	10	15		20
2 и 6	-5	-10	-15		-20
3 и 7	-15	-10	5		10
4 и 8	-20	-15	-10		5

3. Перемещая мышью «руку» вблизи провода, нажимайте левую кнопку мыши на расстояниях r до оси провода, указанных в табли-це 4.2. Значения r и B занесите в таблицу 4.2. Повторите измерения

для трёх других значений тока из таблицы 4.1.

27

		Результаты измерений				Таблица 4.2
r 10 2 , м	1		2		...		10
1
r , м-1
B1 , Тл
B2 , Тл
B3 , Тл
B4 , Тл

Эксперимент 2

1. Закройте окно эксперимента 1, нажав кнопку в правом верх-нем углу внутреннего окна. Запустите, дважды щёлкнув мышью, экс-перимент «Магнитное поле кругового витка с током». Наблюдайте линии индукции магнитного поля кругового витка (контура).

2. Зацепив мышью, перемещайте движок регулятора тока. За-фиксируйте величину тока, указанную в таблице 4.1 для вашей бригады.

3. Перемещая мышью «руку» по оси витка, нажимайте левую кнопку мыши на расстояниях r до оси витка, указанных в табли-

це 4.3. Значения r и B занесите в таблицу 4.3. Повторите измерения для трёх других значений тока из таблицы 4.1.

					Результаты измерений		Таблица 4.3
	r 10 2 , м			1	2	...	10
1			м-3
		3

_(R ² _r³ ₎2

B₁ , Тл

B₂ , Тл

B₃ , Тл

B₄ , Тл

Эксперимент 3

1. Закройте окно эксперимента 2, нажав кнопку в правом верх-нем углу внутреннего окна. Запустите, дважды щёлкнув мышью, экс-перимент «Магнитное поле соленоида». Наблюдайте линии индукции магнитного поля соленоида.

2. Зацепив мышью, перемещайте движок регулятора тока. За-фиксируйте величину тока, указанную в таблице 4.1, для вашей бри-гады.

28

3. Перемещая мышью «руку» по оси соленоида, нажимайте ле-вую кнопку мыши на расстояниях r до оси соленоида, указанных в таблице 4.4. Значения r и B занесите в таблицу 4.4. Повторите изме-

рения для трёх других значений тока из таблицы 4.2.

Таблица 4.4

Результаты измерений

r 10 2 , м	1	2	...	10
B1 , Тл
B2 , Тл
B3 , Тл
B4 , Тл

Обработка данных и анализ результатов

1. Вычислите и запишите в таблицы 4.2–4.4 значения для второй

строки.

2. Постройте на одном листе графики зависимости индукции магнитного поля B прямого провода с током от обратного расстоя-

ния (¹_r) .

3. Постройте на втором листе графики зависимости индукции магнитного поля B на оси витка с током от куба обратного расстоя-

ния		1	.
		3
	(R2	r3 )2

4. На третьем листе постройте графики зависимости индукции магнитного поля на оси соленоида от расстояния до его центра.

5. По тангенсу угла наклона графиков на первых двух листах

определите постоянную,

используя формулы 0

2 (B)

для перво-

I

1

2

(B)

( r )

го чертежа и

0

– для второго (площадь витка

IS

(

1

)

(R2 r 2 )3 / 2

19. R² ).

    6. Вычислите среднее значение магнитной постоянной.

    7. Для магнитного поля соленоида при каждом токе определите протяжённость r области однородности, в которой индукция меня-ется не более чем на 10 % от максимальной. Вычислите среднее зна-чение области однородности.

    8. Запишите ответы и проанализируйте ответ и графики.

29

Контрольные вопросы

1. Что такое магнитное поле?

2. Назовите источники магнитного поля.

3. Какие силы действуют между движущимися зарядами?

4. Во сколько раз магнитная сила меньше электрической для двух движущихся точечных электрических зарядов?

5. Сформулируйте определение квазинейтральности проводов с током.

6. Какие силы и почему действуют между проводами с током?

7. Дайте определение линии индукции магнитного поля. Зачем их рисуют?

8. Запишите закон Био – Савара – Лапласа. В чём он похож на закон Кулона?

9. Сформулируйте принцип суперпозиции для магнитного поля. 10. Дайте определение циркуляции магнитного поля.

11. Сформулируйте и запишите формулу закона циркуляции магнитного поля.

12. Сформулируйте и запишите формулу для магнитного поля прямого провода с током.

13. Как выглядят линии индукции магнитного поля прямого про-вода с током?

14. Сформулируйте и запишите формулу для магнитного поля на оси кругового витка (контура) с током.

15. Что такое магнитный момент витка с током?

16. Какую форму имеет линия индукции, проходящая через центр витка с током?

17. Что такое соленоид и для чего он используется? 18. Чему равно магнитное поле в центре соленоида?

19. Является ли магнитное поле внутри соленоида точно одно-родным?

20. Как определить протяжённость области однородности маг-нитного поля внутри соленоида, если задана точность?

Лабораторная работа № 5 ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ

Запустите программу. Выберите «Электричество и магнетизм» и «Электромагнитная индукция». Нажмите вверху внутреннего окна кнопку с изображением страницы. Необходимое запишите в свой конспект. Закройте внутреннее окно, нажав кнопку с крестом справа вверху этого окна.

30

Цель работы:

знакомство с моделированием явления электромагнитной ин-дукции;

экспериментальное подтверждение закономерностей элек-тромагнитной индукции.

Краткие сведения из теории

Элементарным магнитным потоком dФ_B через физически малый

элемент поверхности площадью dS называется скалярное произведе-ние вектора индукции магнитного поля B на вектор нормали n к дан-ному элементу поверхности и на площадь dS :

dФ_B (Bn)dS .

Магнитным потоком Ф_B через поверхность площадью S назы-

вается сумма всех элементарных потоков через все элементы этой по-верхности (интеграл по поверхности):

Ф_B BdS .

S

Анализируя свойства интеграла в правой части данного соотно-шения, можем получить условия, когда для определения потока не

требуется интегрирование.

Простейший вариант: потока нет ( Ф_B 0), если: 1) B = 0 или

2) вектор магнитной индукции направлен по касательной к поверхно-

сти в любой её точке ( B n ).

Второй вариант: поток есть произведение индукции на площадь Ф_B BS , если (Bn) const , т.е. одновременно выполняются два усло-

вия: вектор индукции направлен по нормали и имеет одну и ту же ве-личину в любой точке поверхности.

Индукцией называется явление возникновения одного поля (на-пример, электрического) при изменении другого поля (например, маг-нитного).

Электромагнитной индукцией называется явление возникнове-ния электрического поля при изменении магнитного поля.

Закон электромагнитной индукции: циркуляция электрического поля по замкнутому контуру Г_0E пропорциональна быстроте измене-

ния потока магнитного поля Ф_B через замкнутую поверхность S₀ (L₀ ) , ограниченную контуром L₀ , по которому рассчитана циркуляция. Ма-тематически:

31

Г_0E ^ФB , t

где знак «–» соответствует правилу Ленца.

В расшифрованном виде EdL			BdS			.
L0	t		S ( L0 )

Врезультате электромагнитной индукции возникает электриче-ское поле с ненулевой циркуляцией. Поле с ненулевой циркуляцией называется вихревым.

Если в таком поле находится проводящее вещество, то в веще-стве возникает вихревой электрический ток, величина которого про-порциональна напряжённости вихревого электрического поля. Такие токи называются токами Фуко.

Если проводящее вещество имеет форму замкнутого контура, тогда циркуляция электрического поля в нём определяет ЭДС, которая в случае электромагнитной индукции называется ЭДС индукции – _инд .

Закон электромагнитной индукции для проводящего контура имеет вид:

_инд ^ФВ . t

Ток, который в этом случае появляется в контуре, называется индукционным.

Используя закон Ома для полной цепи, получим выражение для тока индукции:

i_инд ^инд_R ,

где R – сопротивление контура.

Если имеется замкнутый контур с переменным током, тогда магнитное поле с изменяющимся потоком создаётся собственным то-ком в этом контуре, и в соответствии с законом электромагнитной индукции в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции _{самоинд} .

Явлением самоиндукции называется возникновение ЭДС само-индукции при протекании по проводнику переменного тока.

Закон самоиндукции:

самоинд ^L _dt^{di ,}

где L – индуктивность проводника.

32

Обработка данных и анализ результатов

В данной лабораторной работе используется компьютерная мо-дель, в которой изменяющийся магнитный поток возникает в резуль-тате движения проводящей перемычки по параллельным проводни-кам, замкнутым с одной стороны.

Эта система изображена на рисунке 5.1. Проводящая перемычка движется со скоростью V по параллельным проводам, замкнутым с одной стороны. Система проводников расположена в однородном магнитном поле, индукция которого равна B и направлена перпенди-кулярно плоскости, в которой расположены проводники. Найти ток I в перемычке, если её сопротивление – R , а сопротивлением провод-ников можно пренебречь. Решив задачу в черновике, получите урав-нение для тока в общем виде.

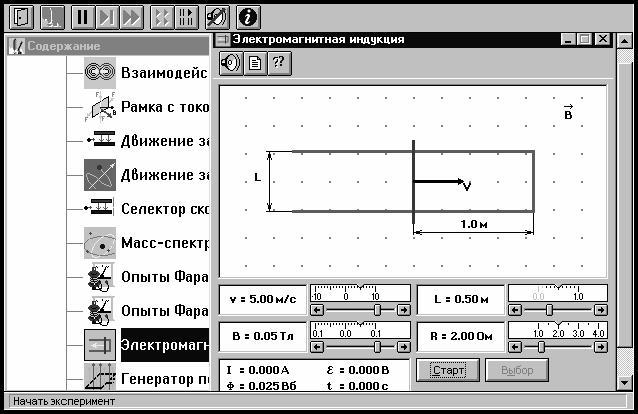
Рис. 5.1. Изменяющийся магнитный поток

1. Запустите эксперимент, щёлкнув мышью по кнопке «Старт». Наблюдайте движение перемычки и изменение магнитного потока Ф (цифры внизу окна).

2. Зацепив мышью, перемещайте движки регуляторов:

L – расстояния между проводами; R – сопротивления перемычки;

B₁ – величины индукции магнитного поля.

Зафиксируйте значения, указанные в таблице 5.1 и под ней, для вашей бригады.

33

				Таблица 5.1
Значения характеристик (не перерисовывать)
Бригады	R , Ом	B1 , мТл	B2 , мТл	B3 , мТл
1 и 5	1	1	40	90
2 и 6	2	2	20	80
3 и 7	1	1	10	70
4 и 8	2	2	-20	100

Для бригад 1–4 L = 1 м, для бригад 5–8 L = 0,7 м.

3. Установив указанное в таблице 5.2 значение скорости движе-ния перемычки, нажмите левую кнопку мыши, когда её маркер раз-мещён над кнопкой «Старт». Значения ЭДС и тока индукции занесите в таблицу 5.2. Повторите измерения для других значений скорости из таблицы 5.2.

		Результаты измерений В = ____ мТл									Таблица 5.2
V , м/c	-10	-8	-6	-4	-2	0	2	4		6		8	10
ЭДС, В
I , мА

4. Повторите измерения для двух других значений индукции магнитного поля, выбирая их из таблицы 5.1. Полученные результаты запишите в таблицы 5.3 и 5.4.

Таблица 5.3

Результаты измерений В = ____ мТл

V , м/c	-10	-8	-6	-4	-2	0	2	4	6	8	10
ЭДС, В
I , мА

		Результаты измерений В = ____ мТл									Таблица 5.4
V , м/c	-10	-8	-6	-4	-2	0	2	4		6		8	10
ЭДС, В
I , мА

Обработка данных и анализ результатов

1. Постройте на одном листе графики зависимости тока индук-ции от скорости движения перемычки при трёх значениях индукции магнитного поля.

34

2. Для каждой прямой определите тангенс угла наклона по фор-

муле: tg( )ЭКСП	I	.
	V
3. Вычислите теоретическое значение тангенса для каждой пря-
мой по формуле: tg( )ТЕОР				BL .
				R
4. Заполните таблицу 5.4 результатов измерений.
		Результаты измерений			Таблица 5.4
Номер измерения				tg( )ЭКСП , Ac/м	tg( )ТЕОР , Ac/м

5. Сделайте выводы по графикам и результатам измерений.

Контрольные вопросы

1. Что называется элементарным магнитным потоком?

2. Что называется магнитным потоком?

3. При каких условиях магнитный поток равен нулю?

4. При каких условиях магнитный поток равен произведению индукции магнитного поля на площадь контура?

5. Сформулируйте определение явления электромагнитной ин-дукции.

6. Сформулируйте закон электромагнитной индукции.

7. Дайте определение циркуляции магнитного поля.

8. Запишите закон электромагнитной индукции в расшифрован-ном виде.

9. Какое поле является вихревым?

10. Что такое ток Фуко?

10. Чем отличается электрическое поле, созданное точечным за-рядом, от электрического поля, появляющегося при электро-магнитной индукции?

10. Сформулируйте закон электромагнитной индукции для замк-нутого проводящего контура.

11. При каких условиях возникает ЭДС самоиндукции?

10. Сформулируйте определение явления самоиндукции.

35

15. Сформулируйте словами закон самоиндукции.

16. Назовите все способы создания переменного магнитного по-тока.

17. Как изменяется со временем магнитный поток в данной рабо-те?

18. Как выглядит поверхность, через которую формируется пе-ременный магнитный поток в данной работе?

19. Какова зависимость магнитного потока от времени в данной работе?

20. Как направлен вектор магнитной индукции в данной работе?

Лабораторная работа № 6 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Выберите «Электричество и магнетизм» и «Свободные колеба-ния в RLC-контуре». Нажмите вверху внутреннего окна кнопку с изо-бражением страницы.

Цель работы:

знакомство с компьютерной моделью процесса свободных за-тухающих колебаний в электрическом колебательном контуре; экспериментальное исследование закономерностей свобод-

ных затухающих колебаний; экспериментальное определение величины индуктивности

контура.

Краткие сведения из теории

Колебательным контуром называется замкнутая цепь, содержа-щая катушку индуктивности с индуктивностью L и конденсатор ём-костью C . Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания то-ка I , заряда конденсатора q и напряжения на элементах.

Напряжение на конденсаторе U_{c C}^q .

ЭДС самоиндукции в катушке L ^dI_dt . Напряжение на резисторе U _R IR .

36

Определение тока I dq .

dt

Дифференциальное уравнение свободных незатухающих коле-

баний:

d 2q 02q 0 ,

1

dt 2

где

– собственная частота контура. Период Т 2 LC .

0

LC

Решение уравнения свободных незатухающих колебаний имеет

вид:

q(t) q

cos( t ) ,

где – начальная фаза.

0

0

Дифференциальное уравнение свободных затухающих колеба-

ний:

d 2q

dq

2

2

q 0 ,

dt2

dt

0

R

где

– коэффициент затухания.

2L

Решение уравнения свободных затухающих колебаний имеет

вид:

q(t) q e- t cos( t ) ,

0

где

2

2

– частота затухающих колебаний.

0

Период свободных затухающих колебаний:

T

2

.

2

2

0

Постоянная времени затухания в контуре^{1 есть время, за}

которое амплитуда колебаний уменьшается в e раз ( e 2,73). Логарифмическим декрементом затухания называется величина,

определяемая формулой ln	q(t)	T T .
	q(t T )
Добротность контура равна Q			.

Методика и порядок измерений

Внимательно рассмотрите рисунок 6.1, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.

37

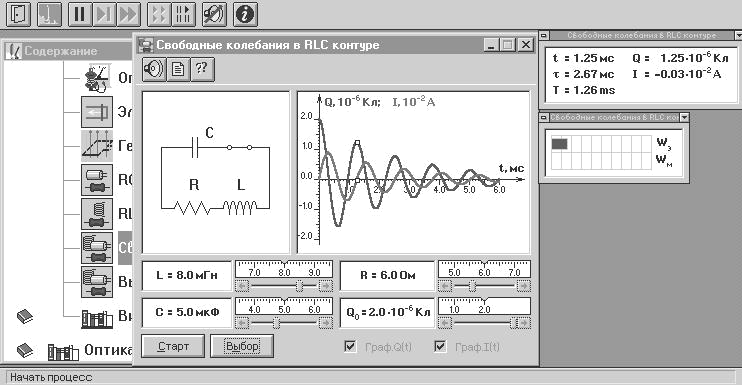
Рис. 6.1. Изменяющийся магнитный поток

Нажмите мышью кнопку «Выбор». Подведите маркер мыши к движку регулятора, нажмите на левую кнопку мыши и, удерживая её в нажатом состоянии, меняйте величину ёмкости конденсатора С и установите числовое значение, равное взятому из таблицы 6.1, для вашей бригады. Аналогичным способом установите величину индук-тивности L в соответствии с таблицей 6.1.

Таблица 6.1

Значения ёмкости конденсатора и индуктивности катушки (не перерисовывать)

Бригада	1	2	3	4	5	6	7	8
C , мкФ	3	3	2,7	2,7	2,4	2,4	2	2
L , мГн	6	7	8	9	10	9	8	7

Установите сопротивления резистора R 1 Ом. Нажав кнопку «Старт», наблюдайте график зависимости заряда конденсатора от времени. Измерьте линейкой значения первых шести амплитуд коле-бания заряда A и запишите их в таблицу 6.2. Меняя сопротивление R , повторите измерения амплитуд и заполните таблицу 6.2.

38

Таблица 6.2

Результаты измерений при С = ___ мкФ, L = ___ мГн, Т = ___ мс

R , Ом	A1 , Кл	A2 , Кл	A3 , Кл	A4 , Кл	A5 , Кл	A6 , Кл	, мс	, с-1
1
2
3
4
5
6
t, мс

Обработка данных и анализ результатов

1. Рассчитайте значения периода колебаний T и запишите в за-головке таблицы 6.2.

2. Рассчитайте время t , при котором измерена соответствующая амплитуда колебания заряда A , и запишите в таблицу 6.2.

3. Постройте на одном чертеже графики экспериментальных за-

висимостей амплитуды колебания заряда А от времени t (6 линий, соответствующих разным R ).

4. Для каждого графика постройте касательную к нему в на-чальный момент времени. Продолжив касательную до пересе-чения с осью времени, определите экспериментальное значе-ние постоянной времени затухания и запишите в таблицу 6.2.

5. Рассчитайте величины коэффициента затухания ¹ и также

внесите в таблицу 6.2.

6. Постройте график зависимости коэффициента затухания от сопротивления резистора R .

6. По графику f (R) определите индуктивность контура L ,

используя формулу ^{L 1 R} .

2

8. Запишите ответ и сформулируйте выводы по ответу и графи-кам.

Контрольные вопросы

1. Что такое колебательный контур?

2. Каковы электрические характеристики резистора, конденса-тора, катушки?

3. Дайте определение гармонических колебаний.

4. Что такое период колебания?

39

5. Какая физическая величина испытывает колебания в колеба-тельном контуре?

5. Напишите формулу для напряжения на конденсаторе.

5. Напишите формулу для напряжения на катушке индуктивно-сти. Какое другое название она имеет?

6. Напишите формулу для напряжения на резисторе. Какое дру-гое название она имеет?

7. Какие законы выполняются для тока и напряжения на отдель-

ных элементах в колебательном контуре?

10. Сформулируйте и запишите в виде формулы закон электро-магнитной индукции в общем виде.

11. Сформулируйте и запишите в виде формулы закон электро-магнитной индукции для проводящего контура.

12. Сформулируйте и запишите в виде формулы закон самоин-дукции.

13. Запишите дифференциальное уравнение для заряда на кон-денсаторе в контуре, где существуют свободные гармониче-ские колебания.

10. Запишите дифференциальное уравнение для заряда на кон-денсаторе в контуре, где существуют свободные затухающие колебания.

10. Напишите формулу циклической частоты свободных гармо-нических колебаний в контуре.

11. Напишите формулу зависимости заряда на конденсаторе от времени при свободных гармонических колебаниях в контуре.

12. Напишите формулу циклической частоты свободных зату-хающих колебаний в контуре.

13. Напишите формулу зависимости заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре.

10. Напишите формулу для коэффициента затухания.

10. Дайте определение постоянной времени затухания.

11. Напишите формулу логарифмического декремента затухания. Что он характеризует?

12. Напишите формулу связи логарифмического декремента за-тухания с коэффициентом затухания.

13. Напишите формулу для добротности контура. Что определяет добротность?

14. Нарисуйте зависимость заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре. Покажите на рисунке, как определяется графически постоянная времени затухания.

40

Лабораторная работа № 7 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В RLC-КОНТУРЕ

Запустите программу. Выберите «Электричество и магнетизм» и «Вынужденные колебания в RLC-контуре». Нажмите вверху внутрен-него окна кнопку с изображением страницы. Закройте внутреннее ок-но, нажав кнопку с крестом справа вверху этого окна.

Цель работы:

знакомство с компьютерным моделированием процессов в колебательном RLC-контуре;

экспериментальное подтверждение закономерностей при вы-нужденных колебаниях в RLC-контуре.

Краткие сведения из теории

Вынужденными колебаниями называются процессы, происхо-дящие в контуре, содержащем конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС, включённые последователь-но и образующие замкнутую электрическую цепь.

Если ЭДС источника меняется по гармоническому закону, то в контуре наблюдаются вынужденные гармонические колебания. При этом ток в контуре также будет переменным, подчиняющимся закону Ома в комплексной форме.

Комплексная величина есть определённая совокупность двух

алгебраических чисел Z A iB Zeⁱ , где A – действительная часть, B – мнимая часть, Z – модуль, – фаза комплексной величины. Гра-

фически Z изображается, как радиус-вектор на комплексной плоско-сти: его длина равна Z , а угол между вектором и горизонтальной (действительной) осью равен .

Комплексный ток и комплексное напряжение:

I (t) I₀ e^{i t} , U (t) U₀ e^{i t} .

Это векторы, которые вращаются с угловой скоростью . Здесь U₀ U₀ e^{i 0u} – комплексная амплитуда напряжения;

I₀ I₀ e^{i 0i} – комплексная амплитуда тока.

41

I₀ и U₀ – комплексные векторы, которые на комплексной плос-

кости неподвижны. Они соответствуют «мгновенной фотографии» реальных комплексных токов и напряжений, сделанной в начальный момент времени (t 0 ).

Комплексная амплитуда – самая комплексная величина, взятая в начальный момент времени.

Импеданс – это отношение комплексной амплитуды напряжения на данном элементе к комплексной амплитуде тока через данный эле-мент.

Модуль импеданса называется полным электрическим сопро-тивлением цепи.

U

U

0 e

i( )

;

.

Z

0

0u

0i

I0

I0

сдвиг фаз

между током

и напряжением

а) для цепи с резистором:	U	R ;	U
	I		0 R ; фазы напряжения и
			I0

тока одинаковые. Импеданс равен R .

б) для цепи с катушкой индуктивности: действует закон элек-тромагнитной индукции (самоиндукции): _с.и. L ^dI_dt .

Используя его и закон Ома для комплексных величин, получим:

^U L

I

U _L L ^d_dt^I ;

_{I I0 e}^{i( t} 0i ^{) dI} _{I0 e} 0i _{(i ) e}^{i t} dt

U_L L(i )I₀ e^{i( t 0 )}.

I (t )

i L X _L i L – импеданс катушки индуктивности.

Напряжение на катушке опережает по фазе ток через неё на /2. в) для цепи с конденсатором:

UC	q		dUC		1 dq			1	I	или
	C		dt		C dt			C
Пусть UC			U0C ei( t0u ) , тогда

^dUC ¹ _{I .} dt C

I C ^dUC C i U_C (t) . dt

42

Найдём отношение	UC		1		i	. Отсюда		i	– ком-
							X C
			i C		C			C
	I

плексное сопротивление (импеданс) конденсатора.

Напряжение на конденсаторе отстаёт по фазе от тока через него на /2.

Модуль комплексного сопротивления (катушки или конденсато-ра) называется реактивным сопротивлением (индуктивным или ёмко-стным). Обозначается символом без крышечки над ним.

Все элементы в контуре соединены последовательно, поэтому для нахождения импеданса контура надо просуммировать импедансы всех элементов:

Z _K R X _L X _C .

После подстановки можем получить модуль импеданса, т.е. полное сопротивление контура:

		2			1		2
Z	R			L			.
					C

Резонансом для тока называется явление резкого увеличения амплитуды колебаний тока при приближении частоты ЭДС к некото-рому значению, называемому резонансной частотой _рез . Нетрудно

видеть, что максимум амплитуды тока будет тогда, когда минимально

полное		сопротивление контура или Z		рез	R	и L	1	, отсюда
							C
						0
							0
	1		, что соответствует частоте свободных колебаний в контуре.
0	LC

Максимум напряжения на конденсаторе соответствует резонан-су для напряжения, который наблюдается при несколько меньшей частоте ЭДС:

		1		R2	2	2	,
					2
рез.U		LC		2L2	0

где₂^R_L – коэффициент затухания для данного контура.

Амплитуда резонансного напряжения на конденсаторе U_0C про-порциональна амплитуде ЭДС и добротности контура Q :

U_0C Q ₀ .

43

При не слишком большом затухании в контуре добротность оп-ределяется соотношением:

Q ,

L

где	L	– называется характеристическим сопротивлением конту-
	C

ра. Чем больше добротность, тем «острее» резонанс. Резонансной кривой называется зависимость амплитуды напря-

жения на конденсаторе от частоты ЭДС.

Методика и порядок измерений

Внимательно рассмотрите рисунок 7.1 для компьютерной модели.

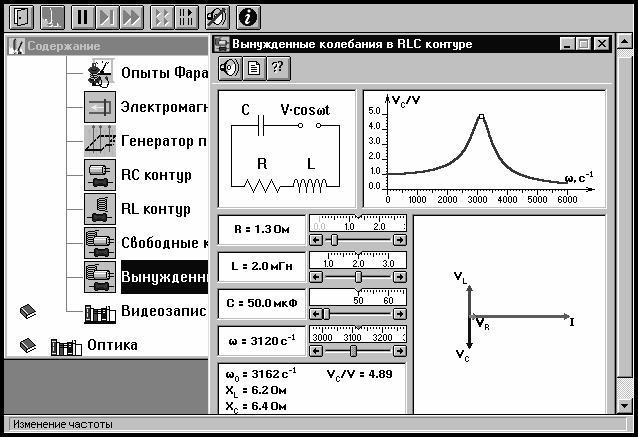
Рис. 7.1. Вынужденные колебания

Перерисуйте необходимое в конспект, используя обозначения, принятые в нашей теоретической части ( ₀ вместо V , U _0C вместо V_C ,

U_0L вместо V_L и U_0R вместо V_R ).

1. Изменяйте величину ёмкости конденсатора и наблюдайте из-менение резонансной кривой.

2. Зацепив мышью, перемещайте движки регуляторов:

R – сопротивления резистора;

L – индуктивности катушки,

и зафиксируйте значения, указанные в таблице 7.1, для вашей бригады.

44

				Таблица 7.1
Значения характеристик (не перерисовывать)
Бригады	R , Ом	L1 , мГн	L2 , мГн		L3 , мГн
1 или 5	1 или 2	1,0	1,7		2,4
2 или 6	2 или 1	1,2	1,9		2,6
3 или 7	1 или 2	1,4	2,1		2,8
4 или 8	2 или 1	1,6	2,3		3,0

3. Повторите измерения для других значений ёмкости конденса-тора C из таблицы 7.2.

Таблица 7.2

Результаты измерения L = ____ мГн

C ,	50	55	60	65	70	75	80	85	90	95	100
мкФ
рез

0

^V0C

₀

1

C

4. Повторите аналогичные измерения для двух других значений индуктивности катушки L , выбирая их из таблицы 7.1.

4. Полученные результаты запишите в таблицы 7.3 и 7.4.

Таблица 7.3

Результаты измерений L = ____ мГн

	C ,		50	55	60	65	70	75	80	85	90	95	100
мкФ
	рез
0
V0C
0
	1
	C

45

Таблица 7.4

Результаты измерений L = ____ мГн

	C ,		50	55	60	65	70	75	80	85	90	95	100
мкФ
	рез
0
V0C
	0
	1
	C

Обработка данных и анализ результатов

1. Постройте на одном листе графики зависимости резонансной частоты _рез от корня из обратной ёмкости ¹_C при трёх значениях

индуктивностиL .

2. Для каждой прямой определите котангенс угла наклона по формуле:

¹

ctg( ) ^C A_эксп.

рез

3. Вычислите теоретическое значение константы A_теор для каж-

дой прямой по формуле A_теор L .

4. Заполните таблицу 7.5 результатов измерений.

	Результаты измерений		Таблица 7.5
Номер измерения		Aэксп, Гн1/2	Aтеор , Гн1/2

Сделайте выводы по графикам и результатам измерений.

Контрольные вопросы

1. Дайте определение вынужденным колебаниям.

2. Что такое колебательный контур?

3. Когда возникают вынужденные гармонические колебания?

4. Как графически изображается комплексная величина?

5. Что такое комплексная амплитуда тока или напряжения?

46

6. Дайте определение импеданса.

6. Что такое полное электрическое сопротивление?

7. Чему равен импеданс резистора?

8. Чему равен импеданс идеальной катушки индуктивности?

10. Как формулируется закон электромагнитной индукции для катушки?

11. Чему равен импеданс конденсатора?

12. Чему равны реактивные сопротивления катушки и конденса-тора?

10. Чему равно реактивное сопротивление последовательно со-единённых катушки и конденсатора?

10. Чему равен импеданс колебательного контура?

11. Чему равно полное сопротивление колебательного контура?

10. Дайте определение резонанса для тока в колебательном кон-туре.

11. На какой частоте наблюдается резонанс для тока в колеба-тельном контуре?

12. На какой частоте наблюдается резонанс для напряжения на конденсаторе в колебательном контуре?

10. Чему равно отношение амплитуд напряжения на конденсато-ре при резонансе и ЭДС?

11. Чему равно характеристическое сопротивление контура? Как оно влияет на добротность?

12. Что такое резонансная кривая контура?

Лабораторная работа № 8 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ МОЩНОСТИ

И КПД ИСТОЧНИКА ПОСТОЯННОГО ТОКА ОТ ВНЕШНЕЙ НАГРУЗКИ

Запустите программу. Выберите «Электричество и магнетизм» и «Мощность и КПД источника постоянного тока». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения.

Цель работы:

знакомство с компьютерным моделированием цепей посто-янного тока;

исследование зависимости мощности и КПД источника по-стоянного тока от сопротивления внешней цепи.

47

Краткие сведения из теории

Закон Ома для полной цепи:

I		E	,
		R r
где I – сила тока в цепи;
E – электродвижущая сила источника тока (ЭДС), включённого в
цепь;
R – сопротивление внешней цепи;
r – внутреннее сопротивление источника тока.
Мощность, выделяемая во внешней цепи:
P I 2 R		E 2		R .	(8.1)
	R r 2
1

Из формулы (8.1) видно, что при коротком замыкании цепи, т.е. при R 0 и при R , эта мощность равна нулю. При всех других конечных значениях R мощность P₁ 0 . Следовательно, функция P₁

имеет максимум. Значение R₀ , соответствующее максимальной мощ-ности, можно получить, дифференцируя P₁ по R и приравнивая пер-вую производную к нулю:

dP1		E 2 R0	r 2 2 R0	r R	0 .	(8.2)
dR			R0 r 4
						всегда положитель-
Из формулы (8.2) с учётом того, что R и r
ны, а E 0 , после несложных алгебраических преобразований полу-
чим:			R0 r .			(8.3)

Следовательно, мощность, выделяемая во внешней цепи, дости-

гает наибольшего значения при сопротивлении внешней цепи, равном внутреннему сопротивлению источника тока (8.3). При этом сила тока в цепи равна:

I	E			Iкз		.	(8.4)
	2r
		2
То есть сила тока в цепи равна половине тока короткого замы-
кания (8.4).
При этом мощность, выделяемая во внешней цепи, достигает
своего максимального значения, равного
P			E 2		.		(8.5)

1max _4r

Когда источник замкнут на внешнее сопротивление, то ток про-

текает и внутри источника, и на внутреннем сопротивлении источни-ка выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла, равна:

P I 2r .	(8.6)
2

48

Следовательно, полная мощность, выделяемая во всей цепи, оп-ределится формулой:

P	P P I 2 R I 2r I 2	(R r) IE .	(8.7)
полн	12

Коэффициент полезного действия источника тока равен:

	P1		R
				.	(8.8)
	P		R r
	полн

Из формулы (8.8) следует, что

P P	P EI I 2r ,	(8.9)
1полн	2

т.е. P₁ изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I 0 и при I ^E_r . Первое

значение соответствует разомкнутой цепи ( R r ), второе – коротко-му замыканию ( R r ). Зависимость КПД от силы тока в цепи с учё-том формул (8.7) – (8.9) примет вид:

1	r	I .	(8.10)
	E

Таким образом, КПД достигает наибольшего значения 1 в

случае разомкнутой цепи ( I 0 ), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.

Зависимость мощностей P₁ , P_полн EI и КПД источника тока от силы тока I в цепи показаны на рисунке 8.1.

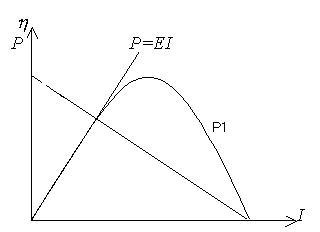
КПД

Рис. 8.1. Зависимость мощности и КПД от силы тока

Из графиков видно, что получить одновременно полезную мощ-ность и КПД невозможно. Когда мощность, выделяемая на внешнем участке цепи P₁ , достигает наибольшего значения, КПД в этот момент

равен 50 %.

49

Методика и порядок измерений

1. Соберите на экране цепь, показанную на рисунке 8.2. Для это-

го сначала щёлкните левой кнопкой мыши над кнопкой ЭДС в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щёлкните левой кнопкой мыши в ра-бочей части экрана, где будет расположен источник ЭДС.

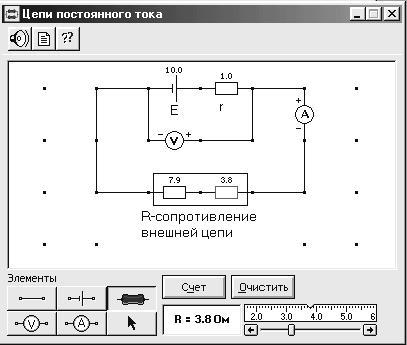
Рис. 8.2. Цепь постоянного тока

2. Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно

кнопку в нижней части экрана) и амперметр (кнопка там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр , измеряющий напряжение на нагрузке.

3. Подключите соединительные провода. Для этого нажмите

кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щёлкайте левой кнопкой мыши в мес-тах рабочей зоны экрана, где должны находиться соединительные провода.

4. Установите значения параметров для каждого элемента. Для

этого щёлкните левой кнопкой мыши на кнопке со стрелкой . Затем щёлкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая её в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 8.1, для вашей бригады.

50

Таблица 8.1

Исходные параметры электрической цепи (не перерисовывать)

Номер бригады	1	2	3	4	5	6	7	8
E , В	10,0	9,5	9,0	8,5	8,0	8,5	9,0	9,5
r , Ом	4,8	5,7	6,6	7,5	6,4	7,3	8,2	9,1

5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных прибо-ров в соответствующие строки таблицы 2.

5. Последовательно увеличивайте с помощью движка сопротив-ление внешней цепи на 0,5 Ом от 2 до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 8.2.

							Таблица 8.2
		Результаты измерений и расчётов
R , Ом	2,0		2,5	3,0	3,5	4,0	5,0	…….	20
U , В
I , А
P1 , Вт
P2 , Вт
Pполн , Вт

Обработка данных и анализ результатов

1. Вычислите по формулам (8.1), (8.6) – (8.8) P₁ , P₂ , P_полн и для

каждой пары показаний вольтметра и амперметра и запишите рассчи-танные значения в таблицу 8.2.

2. Постройте на одном листе миллиметровой бумаги графики

зависимости P₁ f (R) , P₂ f (R) , P_полн f (R) , f (R) и U f (R) . 3. Рассчитайте погрешности измерений и сделайте выводы по

результатам проведённых опытов.

Контрольные вопросы

1. Запишите закон Джоуля – Ленца в интегральной и дифферен-циальной формах.

2. Что такое ток короткого замыкания?

3. Что такое полная мощность?

51

4. 52

   щённый в данную точку поля, к величине этого заряда:

   Как вычисляется КПД источника тока?

5. Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.

6. Верно ли утверждение, что мощность, выделяемая во внут-ренней части цепи, постоянна для данного источника?

7. К зажимам батарейки карманного фонаря присоединили вольт-метр, который показал 3,5 В. Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было на-писано: Р=30 Вт, U=3,5 В. Лампа не горела. Объясните явле-ние.

8. При поочерёдном замыкании аккумулятора на сопротивления R₁ и R₂ в них за одно и то же время выделилось равное коли-

чество тепла. Определите внутреннее сопротивление аккуму-лятора r .

Лабораторная работа № 9

ТЕОРЕМА ОСТРОГРАДСКОГО ГАУССА

ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ВАКУУМЕ

Запустите программу. Выберите «Электричество и магнетизм» и «Теорема Остроградского – Гаусса». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теорети-ческие сведения.

Цель работы:

знакомство с графическим моделированием электростатиче-ских полей;

экспериментальная проверка теоремы Остроградского – Гаусса; экспериментальное определение величины электрической по-

стоянной.

Краткие сведения из теории

Напряжённость электростатического поля в данной точке есть векторная физическая величина, равная отношению силы F , дейст-вующей со стороны поля на неподвижный точечный заряд q₀, поме-

E ^F . q₀

Линиями напряжённости (силовыми линиями) называются ли-нии, проведённые в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряжённости. Линии на-пряжённости проводят так, что они начинаются на положительных зарядах и оканчиваются на отрицательных или уходят в бесконеч-ность (рис. 9.1).

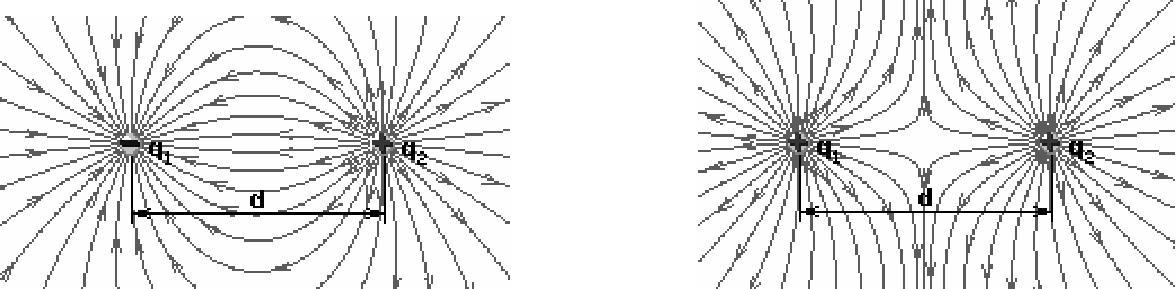
а) б)

Рис. 9.1. Линии напряжённости двух точечных зарядов:

а) разноимённых; б) одноимённых

Принцип суперпозиции электростатических полей: напряжён-ность электростатического поля систем точечных зарядов равна век-

торной сумме напряжённостей полей каждого из этих зарядов в от-

дельности: Е Е_i .

Силовая линия, определяя направление вектора напряжённости, сама по себе не определяет величину модуля вектора напряжённости. Введём условие, связывающее величину модуля вектора напряжённо-сти с числом проводимых линий напряжённости через единицу пло-щади. Для этого выделим в электростатическом поле малую область, в пределах которой электростатическое поле можно считать однород-ным. Проведём в этой области элементарную площадку dS₀ , перпен-

дикулярную к линиям напряжённости. Условимся через эту площадку проводить такое число dФ линий напряжённости, чтобы число линий, приходящихся на единицу поверхности площадки dS₀ , равнялось ве-

личине модуля вектора напряжённости в области этой площадки, т.е. потребуем выполнение условия:

dФ	E .	(9.1)
dS0

53

При выполнении этого условия графического изображения электростатических полей численное значение вектора напряжённо-сти будет связано с густотой линий напряжённости. Тогда число ли-

ний напряжённости, пронизывающих элементарную площадку dS,
	которой образует угол с вектором Е, равно:
нормаль n
	dФ EdS cos ,	(9.2)

где величина dФ называется потоком вектора напряжённости через площадку dS .

Число линий напряжённости Ф, пронизывающих некоторую по-верхность S , назовём потоком вектора напряжённости через эту по-

верхность. Для произвольной замкнутой поверхности			S	поток векто-
ра		сквозь эту поверхность будет равен:
	Е
		Ф EdS cos .		(9.3)

S

Для замкнутой поверхности принято считать положительным направление нормали к элементу поверхности, выходящее из объёма, ограничиваемого поверхностью. Тогда линии напряжённости, выхо-дящие из объёма, создадут положительный поток Ф , а линии, вхо-дящие в объём, создадут отрицательный поток Ф , а результирую-щий поток будет равен алгебраической сумме этих потоков.

Согласно теореме Остроградского – Гаусса, поток вектора на-пряжённости электростатического поля в вакууме через произволь-ную замкнутую поверхность равен алгебраической сумме заключён-ных внутри этой поверхности зарядов, делённой на ₀ :

	1	n
Ф EdS cos		qi .	(9.4)
	0 i 1

Методика и порядок измерений

Рассмотрите внимательно схему опыта и зарисуйте необходимое в свой конспект лабораторной работы.

Как известно, электростатическое поле в вакууме изотропное. Следовательно, количество силовых линий, пересекающих произ-вольную замкнутую поверхность, содержащую внутри себя электри-ческие заряды, будет пропорционально количеству силовых линий, пересекающих замкнутый контур, ограничивающий площадь сечения, в которой находятся электрические заряды этой замкнутой поверхно-сти.

Такое допущение даёт возможность привести в количественное соответствие реальное трёхмерное электростатическое поле с его графической интерпретацией в плоской компьютерной модели, кото-

54

рая показана на рисунке 9.1. Для этого определим число силовых ли-ний Ф , которые фактически должны пересекать произвольную замк-нутую поверхность, внутри которой находится электрический заряд q 1 мкКл. По теореме Остроградского – Гаусса имеем:

Ф	q		1 10 6	1,13 105 (Вб) .
			8,85 10 12
	0

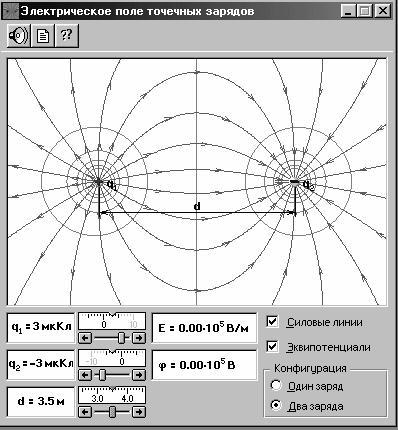
Рис. 9.1. Электрическое поле точечных зарядов

Откройте окно опыта. В нижнем правом прямоугольнике «Кон-фигурация» щёлкните мышью на кнопке «Один заряд». Зацепив мы-шью, перемещайте движок регулятора величины заряда и установите значение q₁ 1 мкКл. Подсчитайте число силовых линий, выходя-

щих из заряда. Их должно быть 6. Следовательно, силовая линия в плоской компьютерной модели опыта соответствует линиям реально-го трёхмерного кулоновского поля:

N	1,13 105	1,88 104 .	(9.5)
	6

На основании таких допущений и оценок создаётся возможность экспериментальной проверки теоремы Остроградского – Гаусса с по-мощью графического компьютерного моделирования электростатиче-ских полей в данной лабораторной работе.

55

Методика и порядок измерений

Эксперимент 1. Постоянное пространственное распределение переменного заряда внутри замкнутой поверхности

1. В нижнем правом прямоугольнике «Конфигурация» нажмите мышью кнопку «Два заряда».

2. Зацепив мышью, перемещайте движок регулятора первого за-ряда до установления значения, указанного в таблице 9.1, для вашей бригады.

Таблица 9.1

Установочные значения физических параметров для проведения экспериментов

Бригады	1	2	3	4		5	6	7	8
			Эксперимент 1
q1 , мкКл	-1	-2	-3	-4		-5	-4	-3	-2
d , м	2	3	4	5		5	4	3	2
			Эксперимент 2
q1 , мкКл	-5	-5	5	-5		-5	-4	-4	-4
q2 ,	+1	+2	+3	+4		+5	+4	+3	+2
мкКл

3. Аналогичным образом установите заданное в таблице 9.1 рас-стояние d между зарядами.

3. Установите мышью на кнопке «Силовые линии» флажок.

4. Установите величину второго заряда 0 и подсчитайте число силовых линий Ф выходящих и Ф , входящих через границы замк-нутого контура, которым в опыте будет являться прямоугольная рам-ка окна опыта. При этом внимательно смотрите за направлением стрелок на силовых линиях поля. Запишите эти данные и разность

• (Ф ) (Ф ) в таблицу 9.2.

Таблица 9.2

Результаты измерений в эксперименте 1. q1 = _____, d =_____

q2 = 0

q2 =+1

q2 =+2

q2 =+3

q2 =+4

q2 =+5

мкКл

мкКл

мкКл

мкКл

мкКл

мкКл

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

56

6. Последовательно устанавливайте заряды: q₂ = +1, +2, +3, +4,

+5 мкКл и выполните п. 5 ещё 5 раз.

Эксперимент 2. Переменное пространственное распределение постоянного заряда внутри замкнутой поверхности

1. Установите значения q₁ и q₂ , соответствующие значениям,

указанным в таблице 1 для вашей бригады.

2. Установите также минимальное расстояние между зарядами d 2 м и на экране окна эксперимента, подсчётом определите числа

• , Ф и Ф.

3. Последовательно увеличивая расстояние между зарядами с шагом 0,5 м, выполните п. 2 ещё 6 раз.

4. Результаты измерений запишите в таблицу 9.3.

Таблица 9.3

Результаты измерений в эксперименте 2. q₁ = _____, q₂ = ____

d =2 м

d = 3 м

d = 4 м

d = 5 м

d =4,5 м

d =3,5 м

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Ф+

Ф

Ф

Обработка данных и анализ результатов

1. Постройте по данным таблицы 9.2 график зависимости потока вектора напряжённости Ф от величины заряда q .

2. По котангенсу угла наклона графика, используя выражения (9.4) и (9.5), определите электрическую постоянную ₀ .

3. По данным, приведённым в таблице 9.3, постройте график за-висимости потока вектора напряжённости Ф от расстояния между за-рядами d .

4. По построенным графикам сделайте анализ результатов и оцените погрешность проведённых измерений.

Контрольные вопросы

1. Какие поля называют электростатическими?

2. Что такое напряжённость электростатического поля?

3. Как определяется направление вектора напряжённости?

4. Что такое поток вектора напряжённости?

57

5. Какая линия называется силовой? Почему они не могут пере-секаться?

5. Какая линия называется эквипотенциальной?

5. Докажите, что эквипотенциальные и силовые линии ортого-нальны.

6. От чего зависит густота силовых и эквипотенциальных ли-ний?

7. В чём заключается физический смысл теоремы Остроград-ского – Гаусса?

8. Рассчитайте, используя теорему Остроградского – Гаусса: а) поле равномерно заряженной бесконечной плоскости; б) поле двух бесконечных параллельных разноимённо заря-

женных плоскостей; в) поле равномерно заряженной сферической поверхности;

г) поле объёмно заряженного шара; д) поле равномерно заряженного бесконечного цилиндра (нити).

5. Каким образом теорема Остроградского – Гаусса и следствия из неё могут быть косвенным подтверждением справедливо-сти закона Кулона?

Лабораторная работа № 10 ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ

Запустите программу «Цепи постоянного тока». с изображением страницы. ния.

«Электричество и магнетизм». Выберите Нажмите вверху внутреннего окна кнопку Прочитайте краткие теоретические сведе-

Цель работы:

знакомство с компьютерным моделированием цепей посто-янного тока;

экспериментальное подтверждение закона Ома для неодно-родного участка цепи.

Краткие сведения из теории

Сила тока прямо пропорциональна количеству заряда, прошед-шего через проводник за единицу времени: I ^dq_dt .

58

Закон Ома для участка цепи: величина силы тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике

I _R¹ U ,

где R – сопротивление проводника.

Резистором называется устройство, обладающее заданным по-стоянным сопротивлением. Реостатом называется переменное сопро-тивление.

Напряжением на участке цепи 1–2 называется физическая вели-чина, определяемая выражением:

U_{12 1 2} E₁₂ .

Закон Ома для неоднородного участка цепи:

_I 1 2 ^E12 _,

R

где ₁ и ₂ – потенциалы концов участка;

E₁₂ – ЭДС, действующая на данном участке цепи.

Применяя закон Ома для неоднородного участка цепи, необхо-димо помнить о правиле выбора знаков: произведение IR следует брать со знаком «+», если направление обхода совпадает с направле-нием тока на этом участке, ЭДС E₁₂ будет иметь знак «+», если её на-

правление (от минуса к плюсу) совпадает с направлением обхода. При этом надо иметь в виду, что вольтметр, подключённый к концам лю-бого участка цепи, будет показывать разность потенциалов между точками подключения прибора, а направление отклонения стрелки прибора будет определяться параметрами внешней цепи.

Таким образом, закон Ома для полной цепи можно записать в

виде
I R rV E12 .	(10.1)

Из формулы (10.1) видно, что при I 0 вольтметр покажет ЭДС источника, включённого в данный участок цепи.

Методика и порядок измерений

В данной лабораторной работе изучается модель электрической цепи, содержащей на одном из своих участков источник электродви-жущей силы (ЭДС). На этом участке, в зависимости от соотношений между параметрами цепи, разность потенциалов между его крайними точками может менять знак, переходя через 0. Соберите на экране опыта замкнутую цепь, показанную на рисунке 10.1.

59

Рис. 10.1. Электрическая цепь постоянного тока

Для этого сначала щёлкните левой кнопкой мыши на кнопке

ЭДС в нижней части экрана. Переместите маркер мыши на ра-бочую часть экрана, где расположены точки. Щёлкните левой кноп-кой мыши в рабочей части экрана, где должен быть расположен ис-точник ЭДС.

Разместите далее последовательно с источником резисторы, вы-полняющие функции его внутреннего сопротивления r и сопротивле-

ния неоднородного участка R₁ (нажав предварительно кнопку

в нижней части экрана), и амперметр (кнопка там же). Затем расположите резистор нагрузки (реостат) и последовательно соеди-нённый с ним амперметр. Над участком цепи расположите вольтметр

, измеряющий разность потенциалов на этом неоднородном участке цепи.

Соедините все указанные приборы в замкнутую цепь. Для этого

нажмите кнопку соединительного провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щёлкайте ле-вой кнопкой мыши в необходимых местах рабочей зоны и сформи-руйте замкнутую цепь, показанную на рисунке 10.1.

60

Установите заданные значения параметров для каждого прибора цепи. Для этого щёлкните левой кнопкой мыши на кнопке со стрел-

кой . Затем щёлкните на данном приборе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая её в нажатом состоянии, установите значения R₁ ,

r , E , которые указаны в таблице 10.1, для вашей бригады.

Таблица 10.1

Значения ЭДС (E₁ и Е₂), внутреннего сопротивления источника (r) и R₁

Бригада	1	2	3	4	5	6	7	8
E1 , В	4,5	5,0	5,5	6,0	6,5	7,0	7,5	8,0
E2 , В	-2,5	-3,5	-4,0	-3,5	-3,0	-4,5	-5,0	-5,5
r , Ом	1,0	1,2	1,4	1,6	1,8	2,0	2,2	2,4
R , Ом	8,0	7,5	7,0	6,5	8,5	9,0	9,5	10,0

Установите сопротивление реостата R 1Ом. Измерьте значения тока и разности потенциалов U (щёлкнув мышью по кнопке «Счёт») и запишите их в таблицу 10.2.

Таблица 10.2

Результаты измерений

Номер	E1 =___, R1 =__, r =___			E1 =__, E2 =__, R1 =__, r =__
измерения
	R , Ом	U , В	I , А	R , Ом	U , В	I , А
1
2
…
10

Увеличивая сопротивление реостата R каждый раз на 1 Ом , по-вторите измерения силы тока и разности потенциалов U по п. 5 и за-полните таблицу 10.2.

61

Включите в схему второй источник питания, как показано на рисунке 10.2, и установите значение E₂ , соответствующее номеру

вашей бригады.

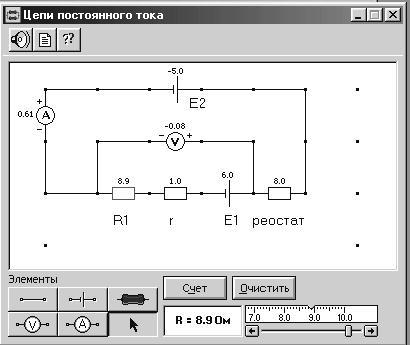
Рис. 10.2. Схема включения второго источника питания

Проведите на второй схеме все измерения п. 5, 6.

Обработка данных и анализ результатов

На одном графике покажите зависимость показаний вольтметра (ось ординат) от силы тока для первой и второй схем (ось абсцисс).

Экстраполируя оба графика до пересечения с осью ординат, оп-ределите по формуле (10.1) экспериментально установленное значе-ние ЭДС ( E₁ ) источника тока, включённого в неоднородный участок

цепи, и сравните его с установочным значением.

По тангенсу наклона прямой к оси I определите полное сопро-тивление участка для двух схем и сравните его значение с установоч-ным значением.

Рассчитайте погрешности измерений и запишите окончательный результат.

62

Контрольные вопросы

1. Дайте определения понятий: разность потенциалов, ЭДС ис-точника тока, напряжение на участке цепи.

2. Что называется сторонней силой? Какова её природа?

3. Выведите Закон Ома в дифференциальной форме.

4. Что называется удельным сопротивлением проводника? От чего оно зависит?

5. Сформулируйте правила Кирхгофа для разветвлённых цепей.

6. Выведите формулы сопротивлений батарей последовательно и параллельно соединённых резисторов.

7. Сформулируйте закон Ома для полной цепи.

8. Объясните принцип действия экспериментальной установки. В чём принципиальная разница первого и второго варианта схем?

Лабораторная работа № 11 ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЧАСТИЦЫ МЕТОДОМ ОТКЛОНЕНИЯ В МАГНИТНОМ ПОЛЕ

Запустите программу «Электричество и магнетизм». Выберите раздел «Масс-спектрометр». Нажмите вверху внутреннего окна кноп-ку с изображением страницы. Прочитайте краткие теоретические све-дения.

Цель работы:

знакомство с компьютерным моделированием движения за-ряженных частиц в магнитном поле;

ознакомление с принципом работы масс-спектрометра; определение удельного заряда частиц.

Краткие сведения из теории

Сила Лоренца – сила, действующая на движущуюся со скоро-стью ν в однородном магнитном поле с индукцией В частицу с заря-дом q:

	(11.1)
F q vB .
Модуль этой силы равен:
F qvB sin ,	(11.2)

где – угол между векторами v и B .

63

Сила Лоренца направлена перпендикулярно скорости частицы, сообщает ей только нормальное ускорение и вызывает искривление траектории частицы.

Если частица влетает в однородное магнитное поле в направле-нии, перпендикулярном линиям магнитной индукции, то частица бу-дет двигаться по дуге окружности, плоскость которой перпендику-лярна линиям индукции. Радиус окружности можно найти из второго закона динамики:

m ^v2 qvB . (11.3)

R

Удельным зарядом частицы называется отношение заряда час-

тицы к её массе. Тогда из формулы (11.3) удельный заряд будет ра-вен:

	q			v	.		(11.4)
	m			RB		2 R
Период обращения частицы T							равен:
			2 m			v
T							(11.5)
				qB

и не зависит от скорости.

Масс-спектрометром называется прибор для разделения ионизо-ванных молекул и атомов (изотопов) по их массам, основанный на воздействии электрических и магнитных полей на пучки ионов, летя-щих в вакууме.

Простейшая модель масс-спектрографа показана на рисунке 11.1.

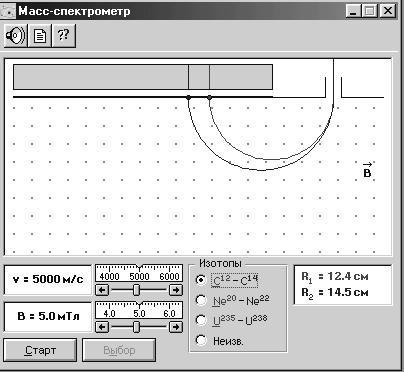
Рис. 11.1. Модель масс-спектрографа

64

Проследите за движением двух изотопов в магнитном поле мо-дельного масс-спектрометра и по секундомеру определите время это-го движения.

Методика и порядок измерений

1. Подведите маркер мыши к движку регулятора величины маг-нитной индукции, нажмите левую кнопку мыши и, удерживая её в нажатом состоянии, двигайте движок, установив числовое значение В, взятое из таблицы 11.1, для вашей бригады.

Таблица 11.1

Значения магнитной индукции

Номер бригады (табл. 11.2)	1	2	3	4	5	6	7	8
В, мТл	1	2	3	4	5	6	7	8
В, мТл	9,0	9,1	9,2	9,3	9,4	9,5	9,6	9,7

2. Аналогичным образом, зацепив мышью движок регулятора скорости, установите минимальное значение скорости 10³ м/с.

3. Нажмите мышью кнопку «Изотопы С¹²-С¹⁴»

4. Нажмите мышью кнопку «Старт» и синхронно секундомер.

2. Запишите в таблицу 11.2 значения радиусов окружностей, по которым двигались эти изотопы (они показаны красным и синим цве-том в правом углу окна) и время движения изотопов в вакуумной ка-мере масс-спектрометра.

Таблицы 11.2

Результаты измерений и расчётов В= _______. Изотопы_______

		ν 103, м/с					1	2	3			4	5	6			7	8	9	10
			R1 , м
		R2 , м
			T1 , с
			T2 , с
		q1			, Кл/кг
		m
1
		q2			, Кл/кг
		m
2
						Табличные значения:					q1	=		,	q2		=
										m					m
										1					2

65

6. Последовательно увеличивая скорость частиц на 10³ м/с, про-делайте п. 4–5 ещё 9 раз и заполните таблицу 11.2.

6. Нажмите мышью кнопку «Изотопы Ne²⁰-Ne²² », проведите из-мерения п. 4–6 и заполните таблицу, аналогичную таблице 11.2.

6. Проведите измерения с изотопами урана и неизвестного хи-мического элемента и заполните таблицы, аналогичные таблице 11.2.

Обработка данных и анализ результатов

1. Вычислите по формуле (11.4) удельные заряды изотопов уг-лерода, неона, урана и неизвестного химического элемента и запиши-те полученные значения в соответствующие таблицы.

2. Используя справочные материалы по физике и химии, опре-делите табличные значения удельных зарядов исследованных изото-пов и сравните их с полученными результатами в опыте.

3. Постройте график зависимости времени пролёта изотопов в камере масс-спектрометра от их скорости и сделайте выводы по ре-зультатам анализа этого графика.

4. Проведите оценку погрешностей проведённых измерений.

Примечание: атомная единица массы (а.е.м.) = 1,660 10 ²⁷ кг. Элементарный заряд е = 1,602 10 ¹⁹ Кл.

Контрольные вопросы

1. Как определяется направление действия силы Лоренца?

2. Почему сила Лоренца не совершает работы?

3. Как будет двигаться заряженная частица в магнитном поле, если угол между векторами B и v меньше /2?

4. Ионы двух изотопов с массами m и m₂ , имеющие одинако-вый заряд и прошедшие в электрическом поле одинаковую ускоряющую разность потенциалов, влетают в магнитное по-ле перпендикулярно силовым линиям магнитного поля. Най-дите отношение радиусов окружностей, по которым будут двигаться ионы в магнитном поле.

4. Определите, во сколько раз изменится радиус окружности, по которой заряженная частица движется в однородном магнит-ном поле, если её кинетическую энергию увеличить в n раз?

4. Определите удельный заряд иона, который в масс-спектро-метре совершает один оборот за 628 мкс в однородном маг-нитном поле с индукцией 50 мТл.

66

7. Пучок ионов, влетающих в вакуумную камеру масс-спектро-метра перпендикулярно силовым линиям однородного магнит-ного поля, расщепляется (рис. 11.2). Определите, какая траек-тория соответствует:

а) большему импульсу, если ионы имеют одинаковые заряды, но разные импульсы; б) большему заряду, если частицы имеют одинаковые импуль-сы, но разные заряды?

Рис. 11.2. Траектория движения ионов

8. Два электрона движутся в одном и том же однородном маг-нитном поле по орбитам с радиусами R₁, R₂ (R₁ R₂). Сравни-те их угловые скорости.

9. В однородном магнитном поле движутся по окружностям протон и -частица, имея равные кинетические энергии. Ка-кая из этих частиц будет иметь орбитальный магнитный мо-мент и период вращения больше и во сколько раз?

10. Заряженная частица влетела в однородное магнитное поле под углом /2 между векторами B и v . Определите, от-личны ли от нуля тангенциальная и нормальная составляю-щие ускорения частицы?

10. Заряженная частица летит прямолинейно и равномерно в од-нородном электромагнитном поле, представленном суперпо-зицией взаимно перпендикулярных электрических (напря-жённостью Е) и магнитных (индукцией В) полей. Найдите скорость движения частицы.

10. Заряженная частица вращается в однородном магнитном поле с индукцией В по окружности радиуса R. Параллельно маг-нитному полю возбуждается электрическое поле напряжённо-стью Е. Определите, сколько времени должно действовать электрическое поле, чтобы кинетическая энергия частицы возросла в два раза?

67

Лабораторная работа № 12 ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ ПОСТОЯННОГО ТОКА

С КОНДЕНСАТОРОМ

Выберите раздел «Электричество и магнетизм» и в нём «Кон-денсаторы в цепях постоянного тока». Нажмите кнопку с изображе-нием страницы во внутреннем окне. Прочитайте теорию.

Цель работы:

знакомство с компьютерным моделированием переходных процессов в цепях постоянного тока;

экспериментальное определение ёмкости конденсатора.

Краткие сведения из теории

Переходным процессом называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процес-са является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгно-венное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными.

Разрядка конденсатора. Если обкладки заряженного конденса-тора ёмкости C замкнуть через сопротивление R , то через это сопро-тивление потечёт ток. Согласно закону Ома для однородного участка цепи

IR U ,

где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора.

Учитывая, что I ^dq_dt и U _C^q , преобразуем закон Ома к виду:

^{dq q} 0 . (12.1) dt RC

• этом дифференциальном уравнении переменные разделяются,

• после интегрирования получим закон изменения заряда конденсато-ра со временем:

		t
q q e		RC ,		(12.2)
0

где q₀ – начальный заряд конденсатора;

е – основание натурального логарифма.

68

Произведение RC , имеющее размерность времени, называется временем релаксации . Продифференцировав выражение (12.2) по времени, найдём закон изменения тока:

	dq			t	,	(12.3)
I		I0e
	dt

где I₀ – сила тока в цепи в момент времени t 0 .

Из уравнения (12.3) видно, что есть время, за которое сила то-ка в цепи уменьшается в е раз.

Методика и порядок измерений

1. Соберите на рабочей части экрана замкнутую электрическую цепь, показанную на рисунке 12.1.

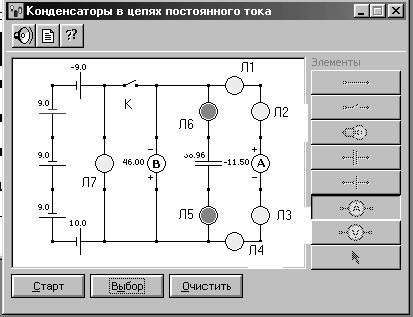
Рис. 12.1. Электрическая цепь

Для этого сначала щёлкните мышью на кнопке ЭДС, рас-положенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора ЭДС, нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину ЭДС и установите 10 В. Аналогичным образом включите в цепь 4 других ис-точника тока. Суммарная величина ЭДС батареи должна соответство-вать значению, указанному в таблице 12.1, для вашей бригады. Таким

69

же образом разместите далее на рабочей части экрана 7 ламп Л1–Л7 (кнопка ), ключ К (кнопка ), вольтметр (кнопка ), ам-

перметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рисунка 12.1 с помощью мон-тажных проводов (кнопка ).

Таблица 12.1

Суммарное значение ЭДС батареи 5 источников тока

Бригада	1	2	3	4	5	6	7	8
ЭДС, В	50	49	48	47	46	45	44	43

2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мы-ши замкните ключ К.

2. После установления в цепи стационарного тока (должны по-гаснуть лампы Л5 и Л6 и светиться лампы Л1–Л4) запишите показа-ния электроизмерительных приборов в таблицу 12.2.

Таблица 12.2

Определение сопротивления лампы

I , А	U , В	R , Ом

4. Нажмите на кнопку «Стоп» и курсором мыши разомкните

ключ К.

4. Двумя короткими щелчками мыши на кнопке «Старт» запус-тите и остановите процесс разрядки конденсатора. Показания ампер-метра будут соответствовать начальному току разрядки конденсато-ра I₀ . Запишите это значение в таблицу 12.3.

Таблица 12.3

Результаты измерений и расчётов

Номер опыта

1

2

3

4

5

Среднее значение

I₀ , А

I, А

, с

• , Ф

70

6. Вновь замкните ключ, зарядите конденсатор и повторите п. 5, 6 ещё 4 раза.

7. Для каждого опыта рассчитайте ^{I I0} – силу тока, которая

2,7

должна быть в цепи разрядки конденсатора через время релаксации

• запишите эти значения в таблицу 12.3.

8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундо-мер.

8. Внимательно наблюдайте за изменением показаний ампер-метра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, рав-

ном или близким к I . Запишите это значение времени ₁ в табли-

цу 12.3.

10. Проделайте опыты п. 8, 9 ещё 4 раза.

Обработка данных и анализ результатов

1. По закону Ома для участка цепи R ¹₄ ^U_I и результатам изме-

рений, приведённым в таблице 12.2, определите сопротивление одной лампы.

^{2. По формуле} C (при разрядке конденсатора квазистацио-

6R

нарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в табли-

цу 12.3.

3. Рассчитайте погрешности измерений и сформулируйте выво-ды по результатам проделанной работы.

Контрольные вопросы

1. Что представляет собой конденсатор и от чего зависит его ёмкость?

2. Выведите формулы ёмкости плоского, цилиндрического и сферического конденсаторов.

3. Как изменяется разность потенциалов на обкладках конден-сатора при его зарядке и разрядке?

4. Какой ток называется квазистационарным?

5. Выведите формулы электроёмкости батареи последовательно и параллельно соединённых конденсаторов.

6. Что такое время релаксации?

7. Объясните принцип работы экспериментальной установки.

71

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Дмитриева, В.Ф. Основы физики : учеб. пособие для вузов / В.Ф. Дмитриева, В.Л. Прокофьев. – 2-е изд., испр. и доп. – М. :

Высш. шк., 2003. – 528 с.

2. Детлаф, А.А. Курс физики : учеб. пособие для втузов / А.А. Дет-лаф, Б.М. Яворский. – 4-е изд., испр. – М. : Академия, 2003. – 720 с.

3. Курс физики : учебник для вузов : в 2 т. / В.В. Арсентьев, В.Я. Кирпиченков, С.Ю. Князев [и др.] ; под ред. В.Н. Лозов-

ского. – СПб. : Лань, 2000. – Т. 2. – 592 с.

4. Присяжнюк, Ю.В. Физика. Теория и практика : учеб. пособие для вузов. В 4 ч. Ч. 2. Электричество и магнетизм / Ю.В. При-сяжнюк, В.В. Глебов, С.В. Кирсанов. – Шахты : Изд-во ЮРГУЭС, 2003. – 133 с.

5. Трофимова, Т.И. Курс физики : учеб. пособие / Т.И. Трофимо-

ва. – 13-е изд., стер. – М. : Академия, 2007. – 560 с.

Учебное издание

ФИЗИКА

Лабораторный практикум

В 4 частях