
- •17. Пространство Rm . Последовательности в Rm и их свойства.
- •19. Теорема о непрерывном образе линейно связного множества и ее следствия.
- •22. Т. Достаточное условие дифференцируемости.
- •25. Частные производные высшего порядка. Теорема о равенстве смешанных производных. Непрерывно дифференцируемые и k-непрерывно дифференцируемые функции. Дифференциалы первого и высших порядков.
- •26. Т. Формула Тейлора с остаточным членом в форме Лагранжа.
- •27. Локальный экстремум функции многих переменных. Необходимое условие локального экстремума. Достаточное условие локального экстремума.
- •35. Собственные интегралы, зависящие от параметра. Теоремы о непрерывности, о дифференцировании и об интегрировании интеграла по параметру.
35. Собственные интегралы, зависящие от параметра. Теоремы о непрерывности, о дифференцировании и об интегрировании интеграла по параметру.
Пусть
функция f(x,y)
определена в прямоугольнике P = [a, b] ×
[c, d] и при каждом фиксированном у
∈[c,
d] существует интеграл
 .
Функция
.
Функция
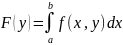 у ∈[c,
d] называется интегралом,
зависящим от параметра.
у ∈[c,
d] называется интегралом,
зависящим от параметра.
Т.
о непрерывности интеграла по параметру.
Пусть функция f(x,y)
непрерывна на прямоугольнике Р и
.
Тогда функция
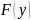 непрерывна на отрезке [c, d].
непрерывна на отрезке [c, d].
Док-во.
Воспользуемся определением Гейне.
Пусть
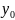 ∈[c,
d] – произвольная точка. Выберем
произвольную последовательность
∈[c,
d] – произвольная точка. Выберем
произвольную последовательность
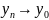 ,
,
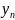 ∈[c,
d], n∈N.
∈[c,
d], n∈N.
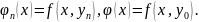
Функция
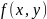 ,
непрерывная на замкнутом прямоугольнике
Р, равномерно непрерывна на нем, поэтому
,
непрерывная на замкнутом прямоугольнике
Р, равномерно непрерывна на нем, поэтому
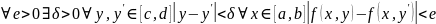 .
.
Пусть
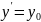 ,
а т.к.
,
то
,
а т.к.
,
то
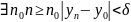 .
Тогда при
.
Тогда при
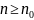 и при
и при
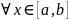 будет выполняться
будет выполняться
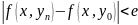 ,
т.е.
,
т.е.
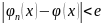 .
Это значит, что функ.послед. (
.
Это значит, что функ.послед. (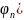 равномерно на
равномерно на
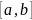 сходится к функции
сходится к функции
 .
По теореме об интегрируемости предела
функ.послед.
.
По теореме об интегрируемости предела
функ.послед.
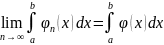 ,
т.е.
,
т.е.
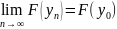 .
Это
означает непрерывность функции F
в произвольной точке
∈[c,
d].
.
Это
означает непрерывность функции F
в произвольной точке
∈[c,
d].
Т.
о дифференцировании интеграла по
параметру.
Пусть функция f(x,y)
непрерывна на прямоугольнике Р, имеет
там непрерывную частную производную
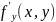 и
и
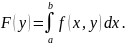 Тогда функция
имеет на отрезке [c, d] производную
Тогда функция
имеет на отрезке [c, d] производную
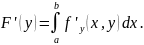
Док-во.
Пусть
∈[c,
d] – произвольная точка. Выберем
произвольную последовательность
,
∈[c,
d], n∈N.
Тогда
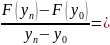
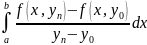 .
.
По
т. Лагранжа
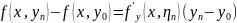 ,
где
,
где
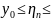 =>
=>
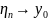 при
при
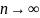 .
Тогда
.
Тогда
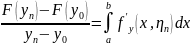 .
.
По
условию
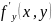 непрерывна на прямоугольнике Р. Поэтому
перейдем к пределу
непрерывна на прямоугольнике Р. Поэтому
перейдем к пределу
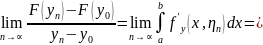
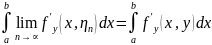 .
По определению Гейне предела функции
производная
.
По определению Гейне предела функции
производная
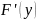 существует, причем
существует, причем
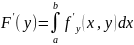 .
.
Т.к.
∈[c,
d] – произвольная точка, то
существует для
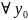 ∈[c,
d] и
.
Т.к.
непрерывна на прямоугольнике, то
∈[c,
d] и
.
Т.к.
непрерывна на прямоугольнике, то
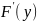 непрерывна на [c, d].
непрерывна на [c, d].
Т.
об интегрировании интеграла по параметру.
Пусть функция f(x,y)
непрерывна на прямоугольнике Р и
.
Тогда
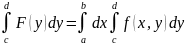 ,
т.е.
,
т.е.
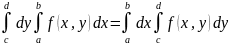 .
.
36. Равномерная сходимость несобственных интегралов, зависящих от параметра. Критерий Коши. Признак Вейерштрасса. *Признаки Абеля и Дирихле равномерной сходимости несобственных интегралов.
Несобственный
интеграл
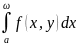 сходится
равномерно
относительно
параметра
у на [c,
d], если для
сходится
равномерно
относительно
параметра
у на [c,
d], если для
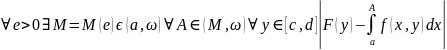 <e.
<e.
Т.
критерий Коши равномерной сходимости
несобственных интегралов.
Несобственный
интеграл
сходится
равномерно на [c,
d] ↔
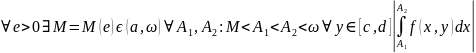 <e.
<e.
Т.
признак Вейерштрасса равномерной
сходимости несобственных интегралов.
Пусть на мн-ве Р имеет место равенство
f(x, y) ≤ g(x) и интеграл
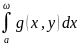 сходится. Тогда
сходится равномерно на [c, d].
сходится. Тогда
сходится равномерно на [c, d].
Док-во.
По критерию Коши. Т.к.
сходится, то
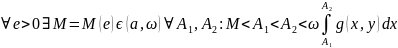 <e.
<e.
Но
тогда
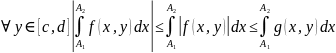 .
По критерию Коши
.
По критерию Коши
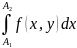 сходится равномерно на
сходится равномерно на
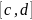 .
.
Т.
признак Абеля.
Пусть на мн-ве P = [a, +∞) × [c, d] функция
f(x, y) = α(x, y)β(x, y), функция β(x, y) ограничена
на Р и монотонна по х при любом
фиксированном y ∈
[c, d],
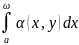 сходится равномерно на [c, d]. Тогда
сходится равномерно на [c, d]. Тогда
 сходится
равномерно на [c, d].
сходится
равномерно на [c, d].
Т.
признак Дирихле.
Пусть на мн-ве P = [a, +∞) × [c, d] функция
f(x, y) = α(x, y)β(x, y), функция β(x, y) монотонна
по х при любом фиксированном y ∈
[c, d] и равномерно на [c, d] сходится к 0 при
x → +∞.
Пусть также
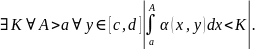 Тогда
сходится
равномерно на [c, d].
Тогда
сходится
равномерно на [c, d].
37. Теоремы о непрерывности, о дифференцировании и об интегрировании несобственного интеграла по параметру.
Т.
о непрерывности несобственного интеграла
по параметру.
Пусть функция f(x, y) непрерывна на мн-ве
P = [a, +∞) × [c, d] и собственный интеграл
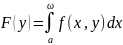 сходится равномерно на [c, d]. Тогда
непрерывна на [c, d].
сходится равномерно на [c, d]. Тогда
непрерывна на [c, d].
Док-во.
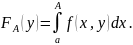 Возьмем
произвольное е>0. Т.к. несобственный
интеграл сходится равномерно, то
Возьмем
произвольное е>0. Т.к. несобственный
интеграл сходится равномерно, то
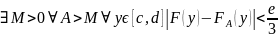 .
Закрепим такое А.
.
Закрепим такое А.
Пусть
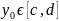 - произвольная точка. Преобразуем
приращение функции F
в этой точке
- произвольная точка. Преобразуем
приращение функции F
в этой точке
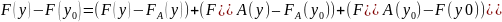 .
Согласно выбору А имеем оценки
.
Согласно выбору А имеем оценки
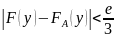 ,
,
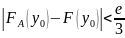 .
.
Интеграл
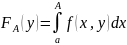 является
собственным и является функцией,
непрерывной на отрезке
.
Тогда
является
собственным и является функцией,
непрерывной на отрезке
.
Тогда
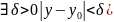 .
.
Тогда
при условии
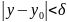
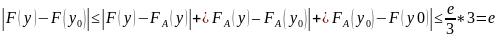 .
Это означает, что
непрерывна в точке
.
Т.к.
– произвольная, то
непрерывна на отрезке.
.
Это означает, что
непрерывна в точке
.
Т.к.
– произвольная, то
непрерывна на отрезке.
Т.
о дифференцировании несобственного
интеграла по параметру. Пусть
функция f(x, y) непрерывна на мн-ве P и
частная производная
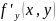 существует и непрерывна на Р, интеграл
существует и непрерывна на Р, интеграл
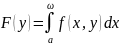 сходится на
,
сходится на
,
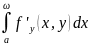 сходится равномерно на
.
Тогда функция
дифференцируема на
и верно равенство
сходится равномерно на
.
Тогда функция
дифференцируема на
и верно равенство
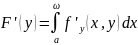 .
.
Док-во.
Возьмем последовательность
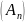 такую ,что
такую ,что
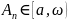 при
при
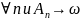 .
Рассмотрим последовательность функций
.
Рассмотрим последовательность функций
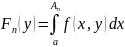 .
Применяя теорему о дифференцировании
собственного интеграла по параметру
получим
.
Применяя теорему о дифференцировании
собственного интеграла по параметру
получим
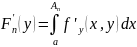 .
.
Последовательность
(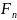 )
сходится в каждой точке отрезка
к функции F,
а последовательность (
)
сходится в каждой точке отрезка
к функции F,
а последовательность (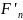 )
сходится равномерно к функции
.
Следовательно, по т.о дифференцировании
предела функциональной последовательности
имеем
)
сходится равномерно к функции
.
Следовательно, по т.о дифференцировании
предела функциональной последовательности
имеем
 ,
т.е.
.
,
т.е.
.
Т.
об интегрировании несобственного
интеграла по параметру.
Пусть функция f(x, y) непрерывна на мн-ве
P = [a, +∞) × [c, d] и собственный интеграл
сходится равномерно на [c, d]. Тогда верно
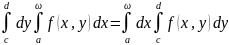 .
.
Док-во.
Возьмем последовательность
такую ,что
при
.
Рассмотрим последовательность функций
.
По теореме об интегрировании собственного
интеграла по параметру
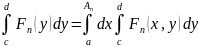 .
.
Каждая
функция
непрерывна на отрезке
и последовательность (
)
сходится равномерно к функции F.
Тогда возможен предельный переход по
знаком интеграла
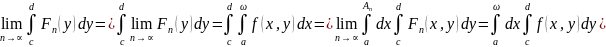 .
.
38. Длина кривой. Определение криволинейных интегралов первого и второго рода по параметризованной гладкой кривой.
Т. о длине кривой.
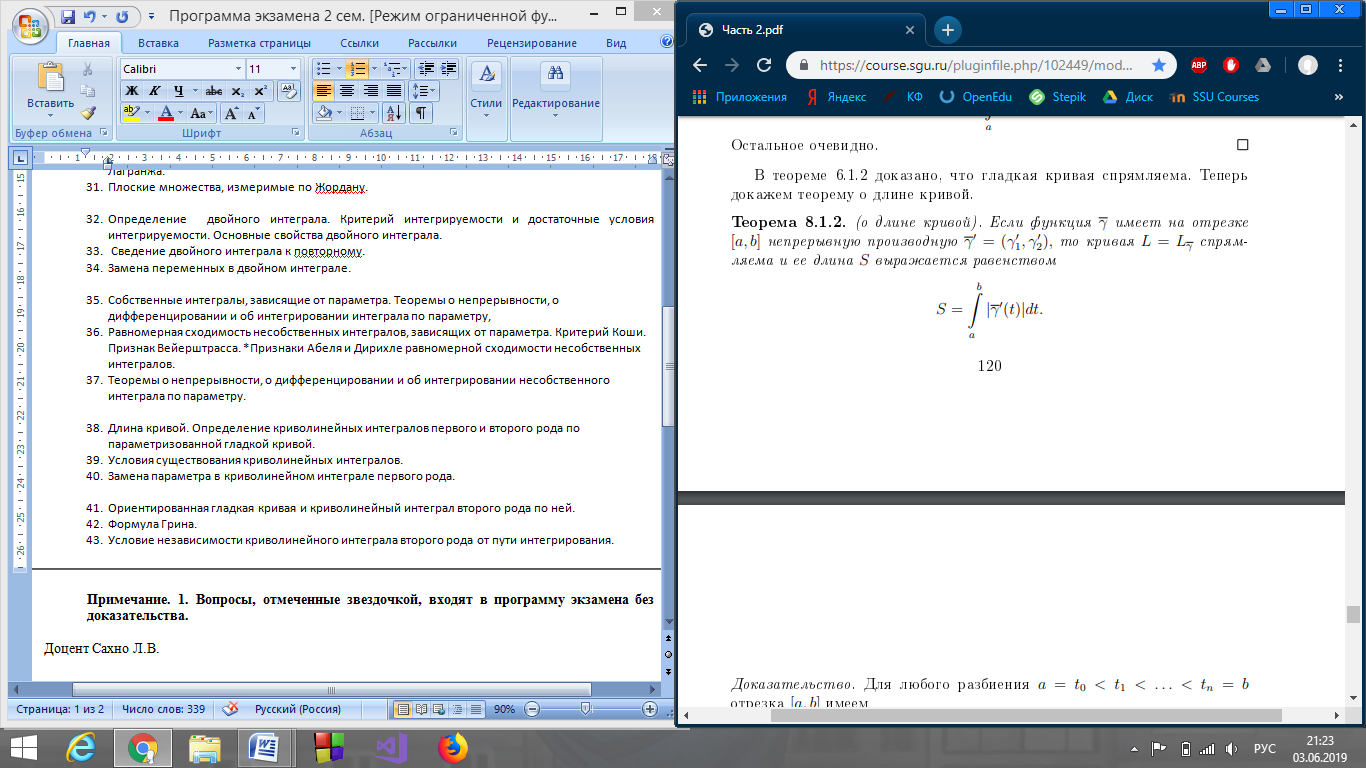
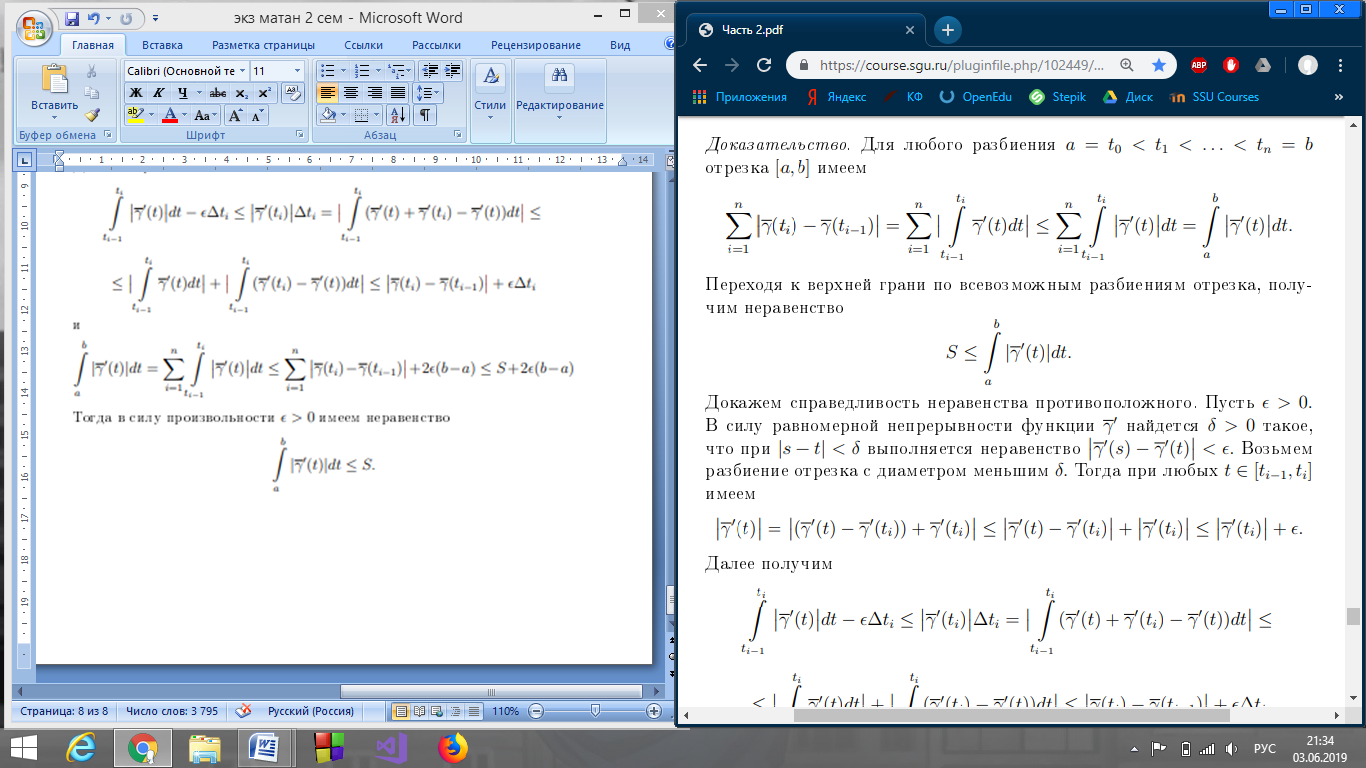
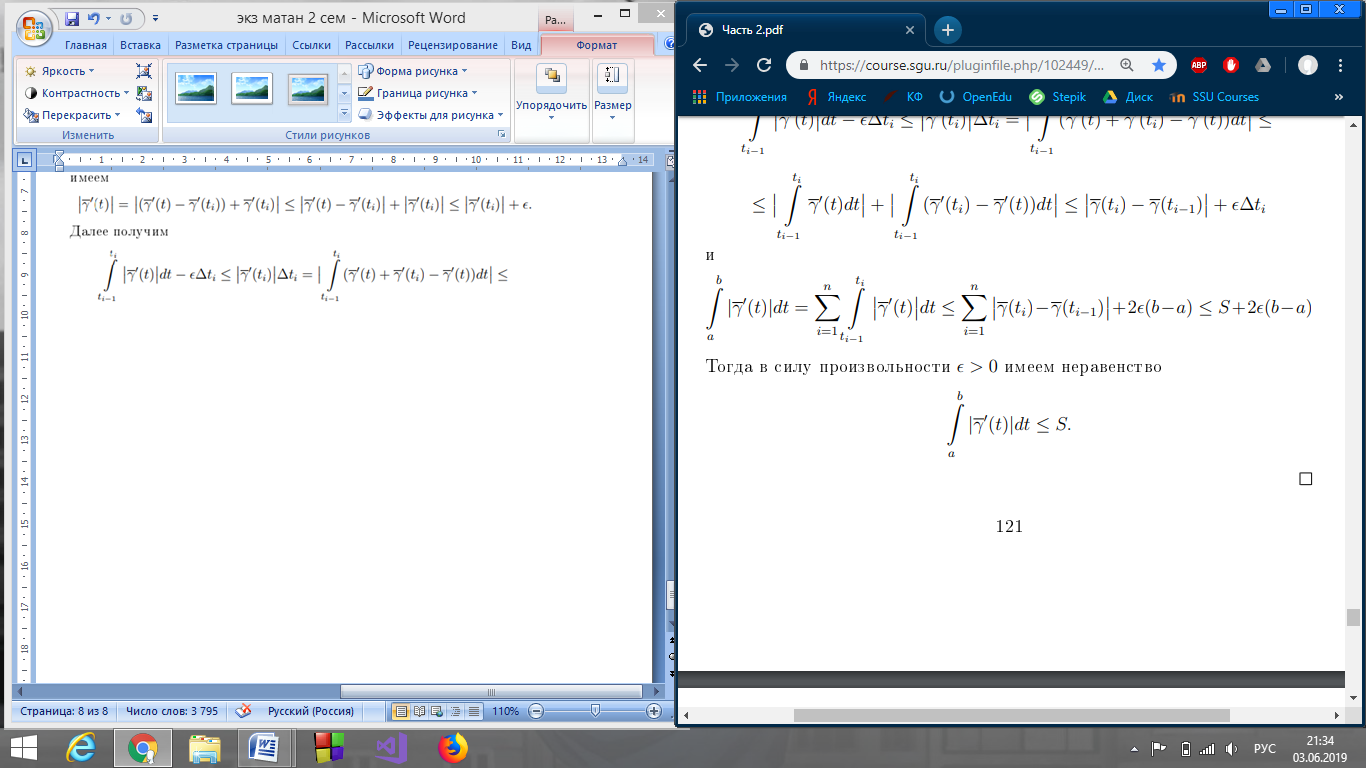
Определение криволинейных интегралов первого и второго рода по параметризованной гладкой кривой.

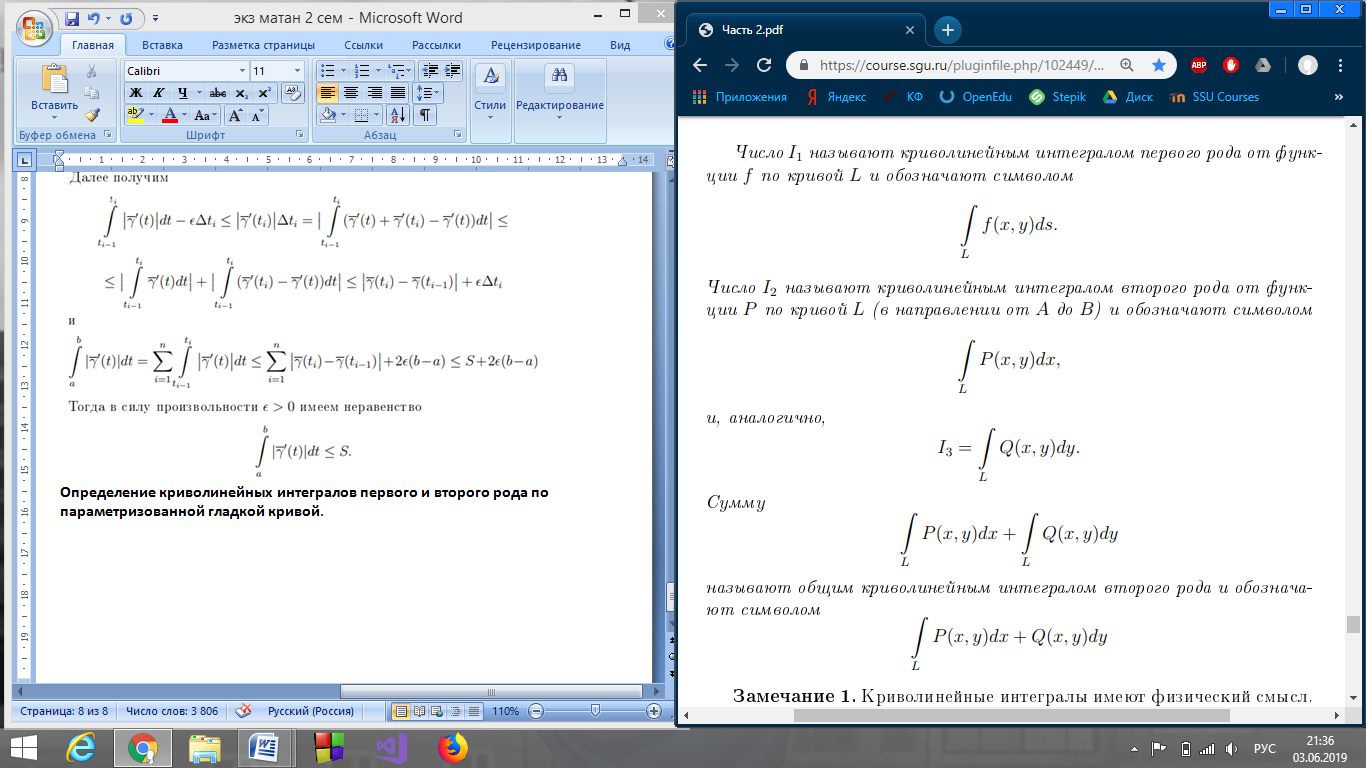
39. Условия существования криволинейных интегралов.
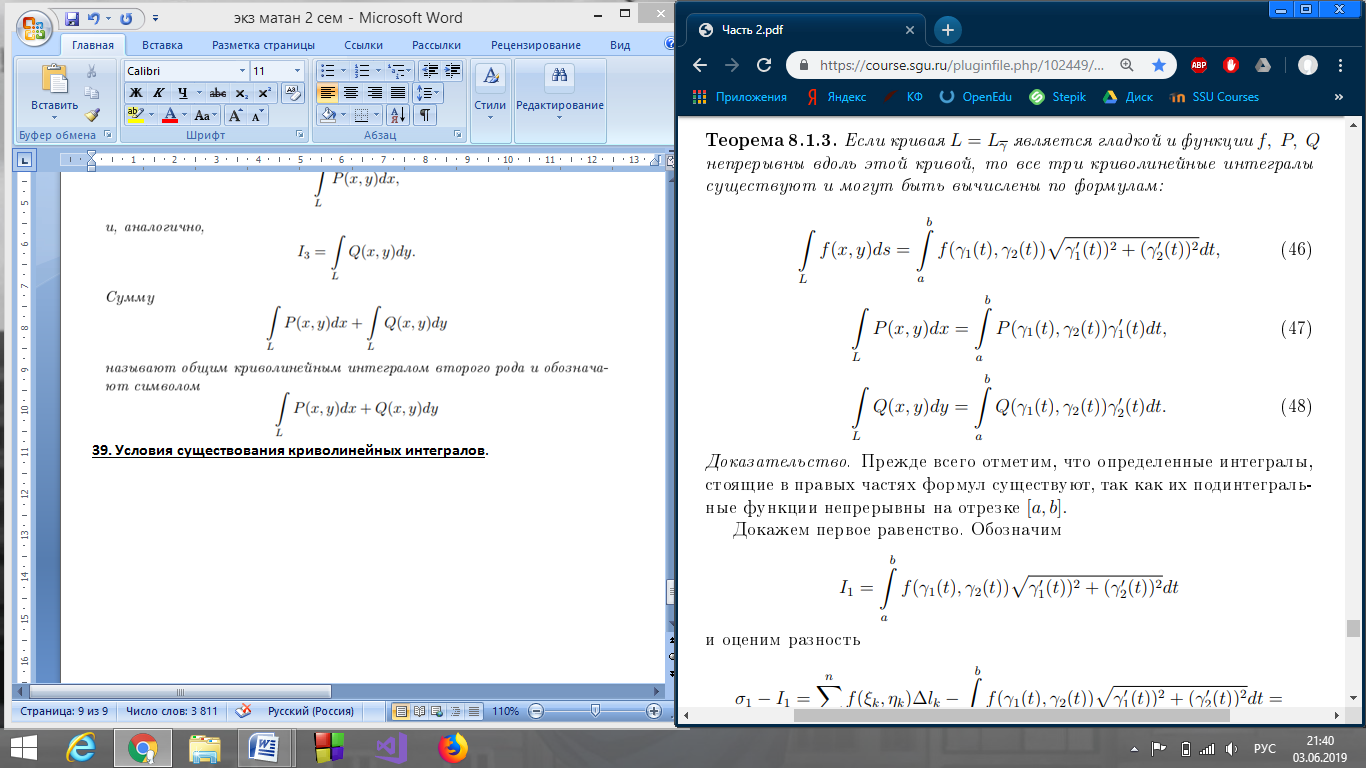
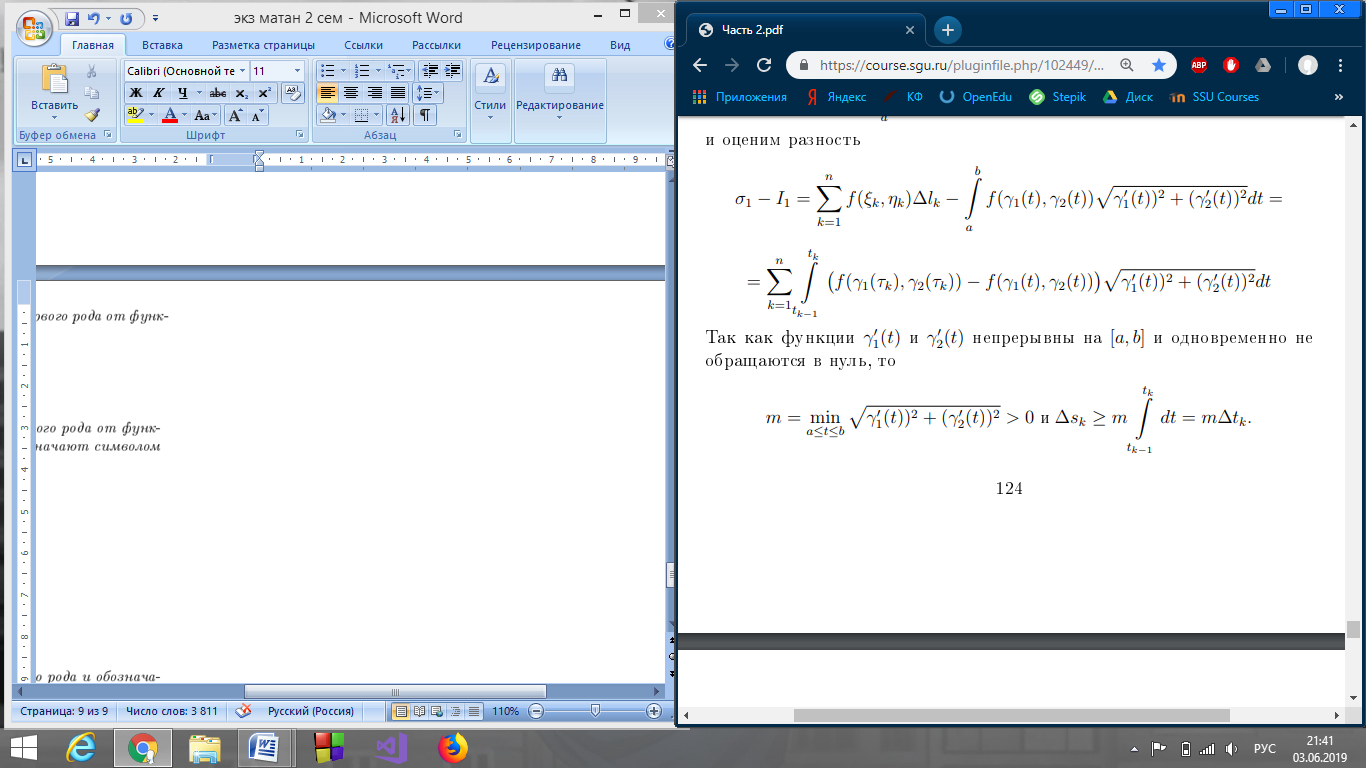
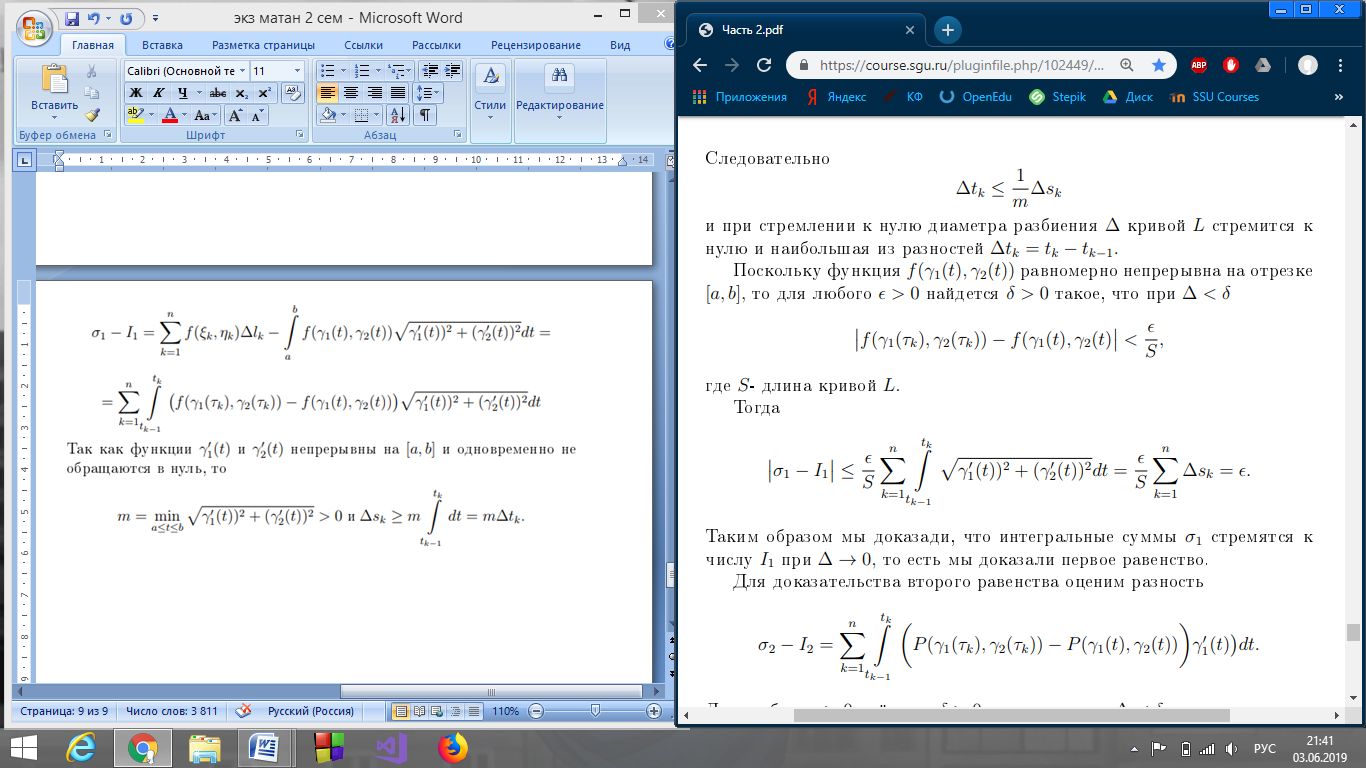
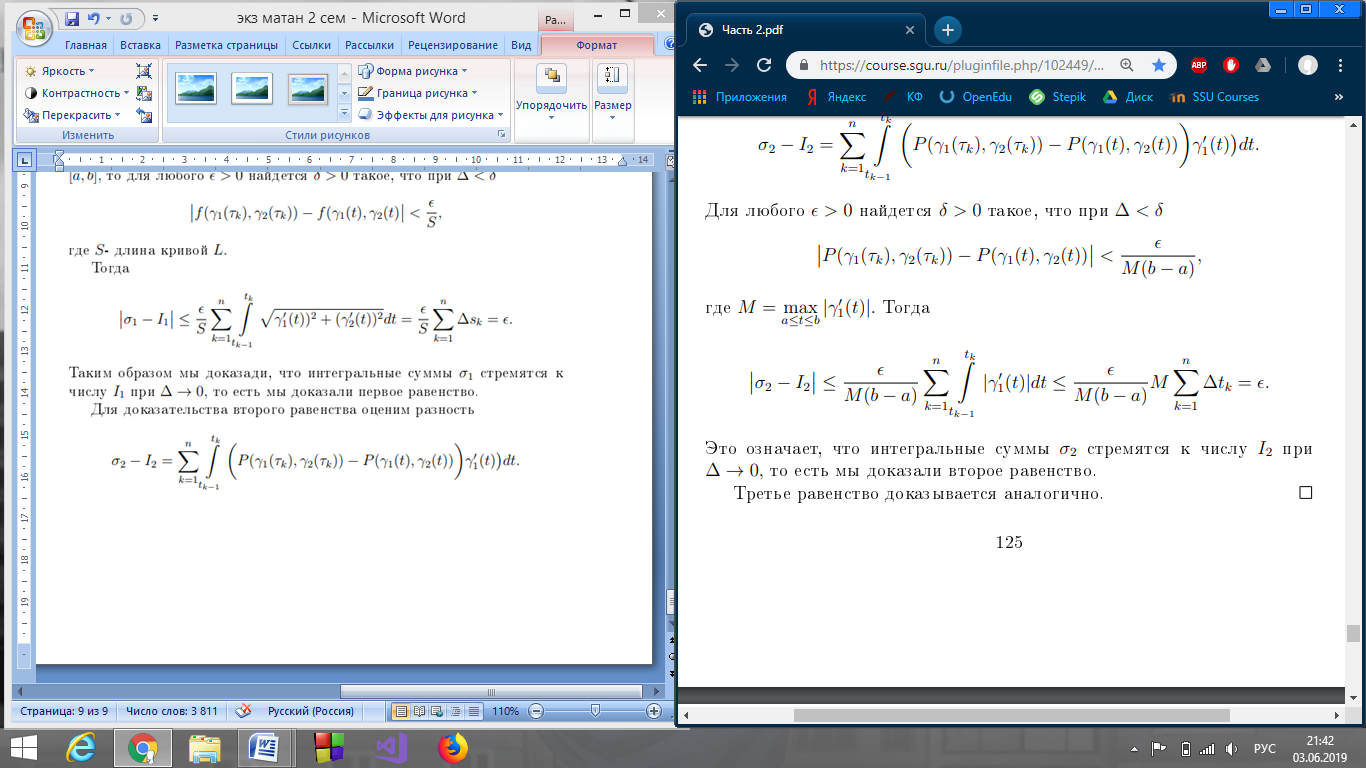
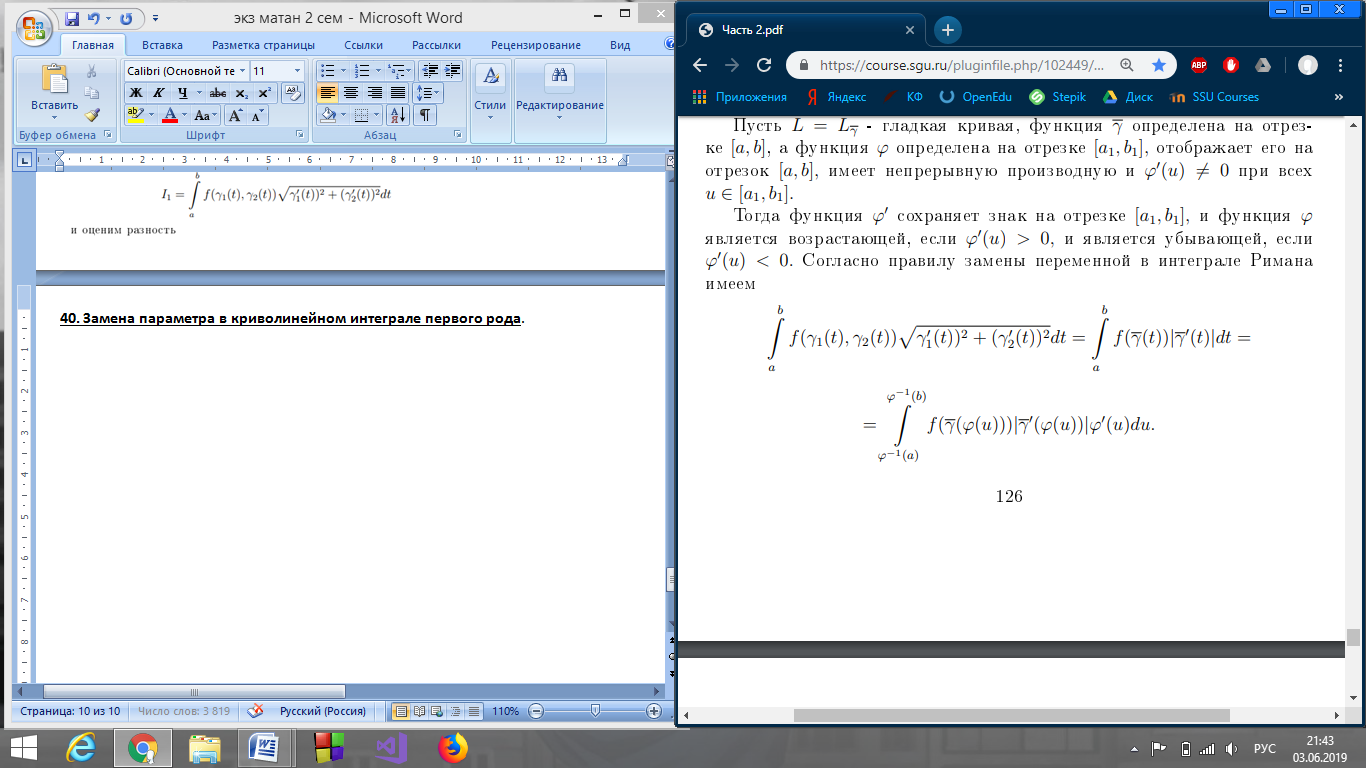
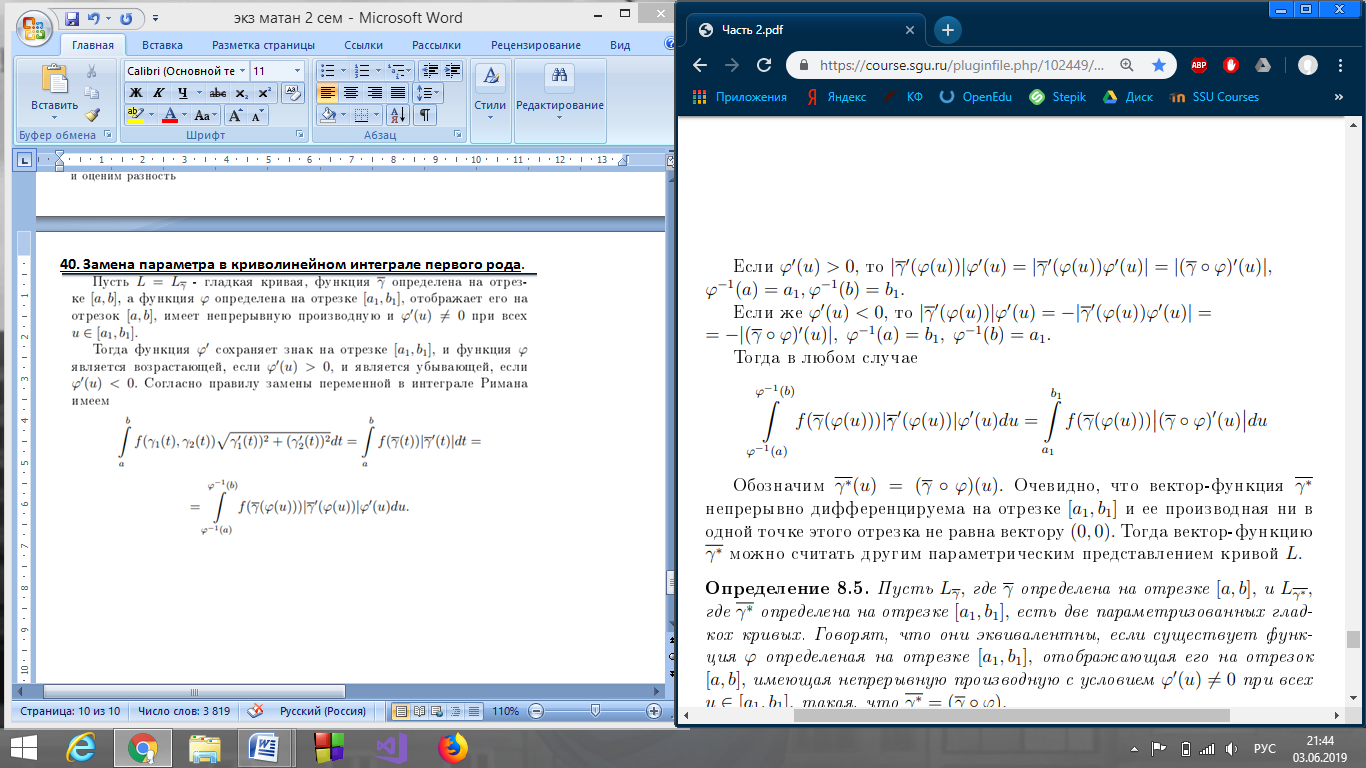
40. Замена параметра в криволинейном интеграле первого рода.
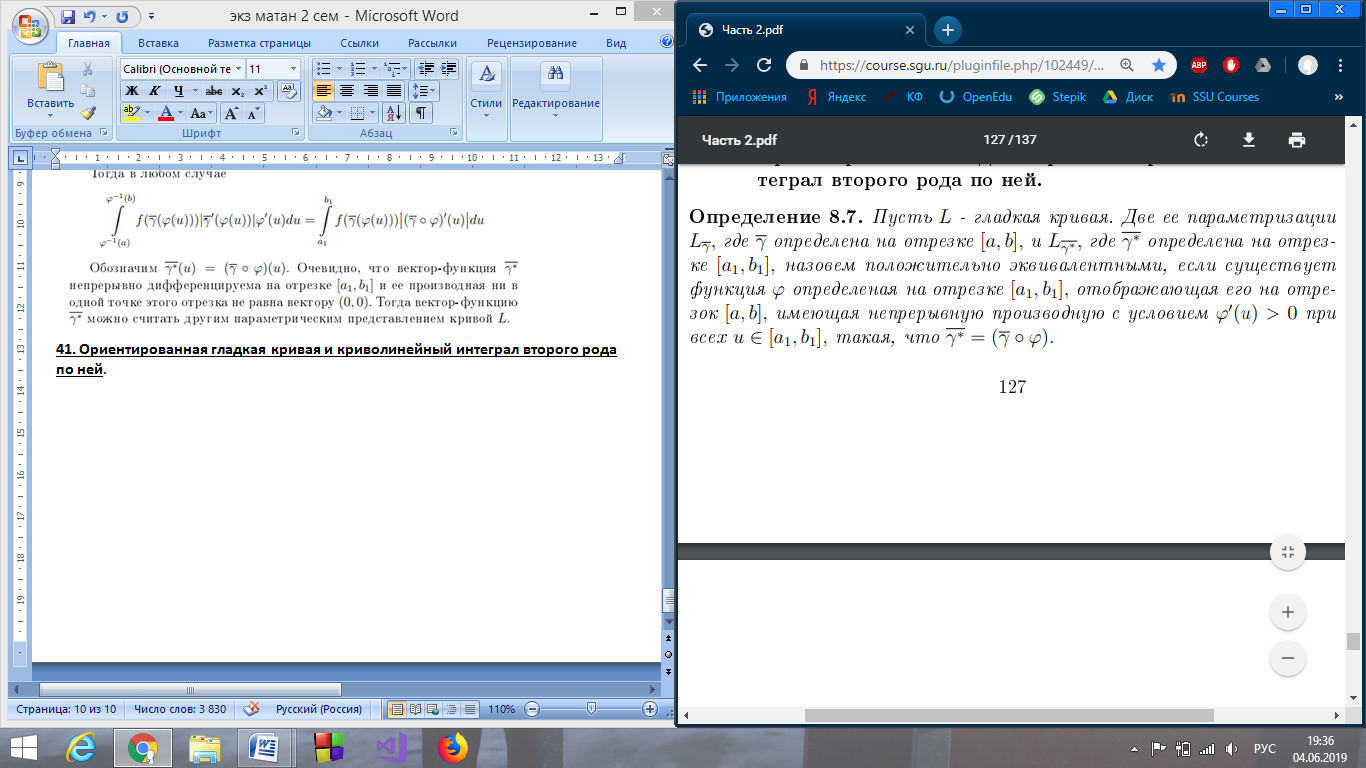
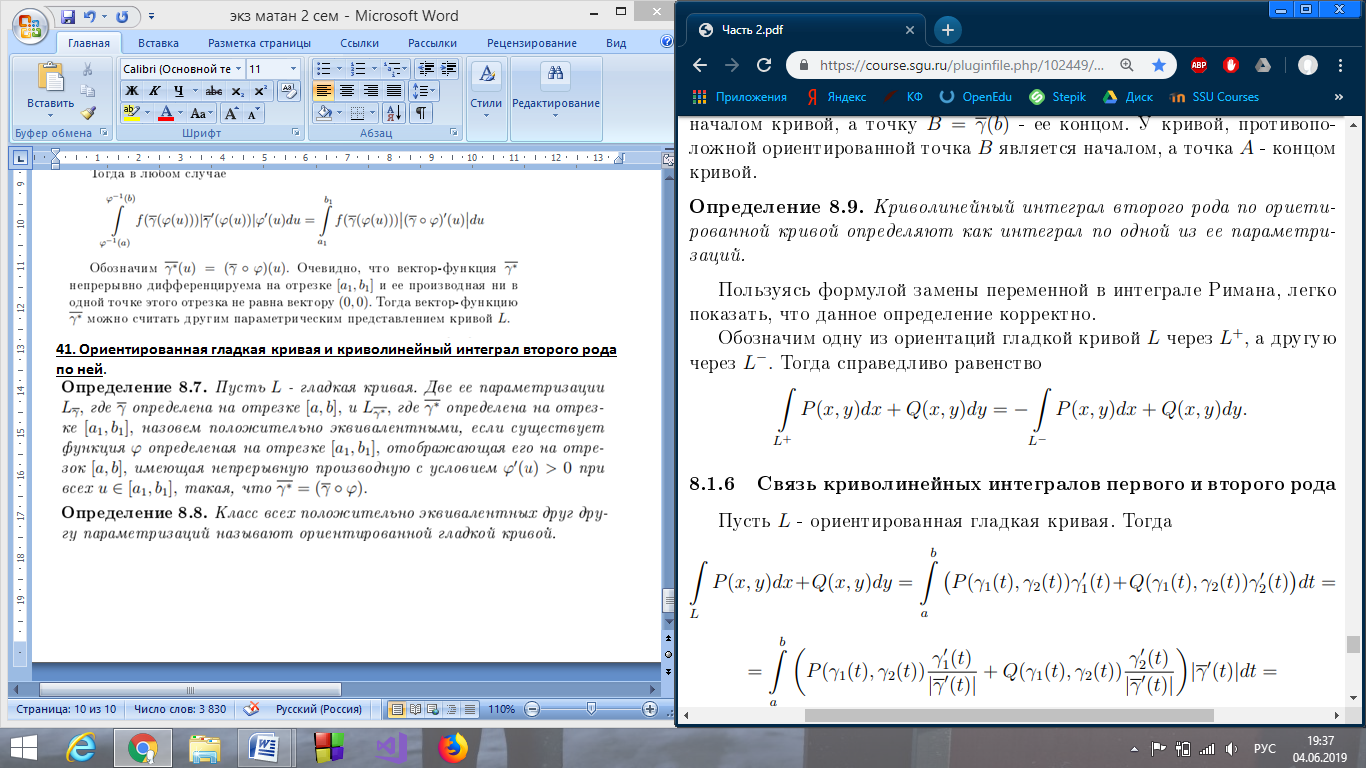
41. Ориентированная гладкая кривая и криволинейный интеграл второго рода по ней.
![]()
42. Формула Грина.
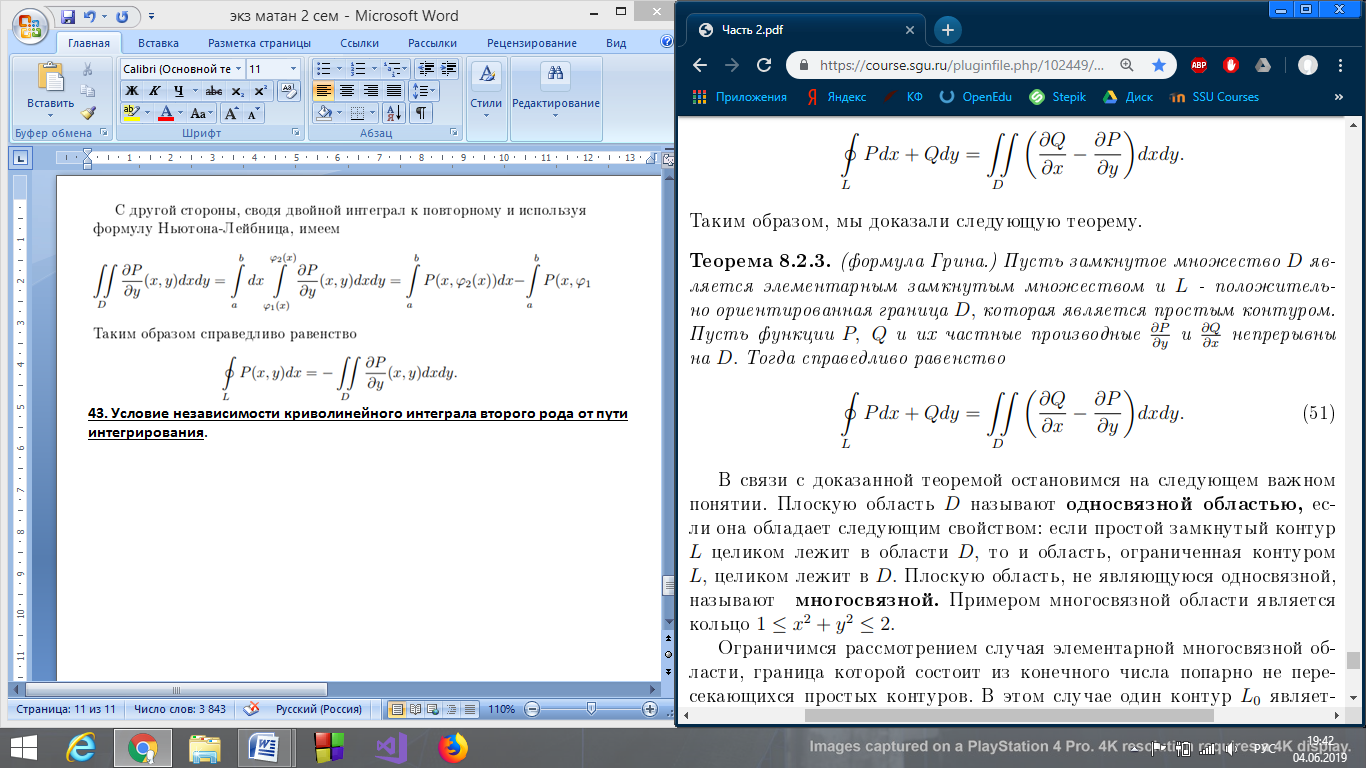
43. Условие независимости криволинейного интеграла второго рода от пути интегрирования.
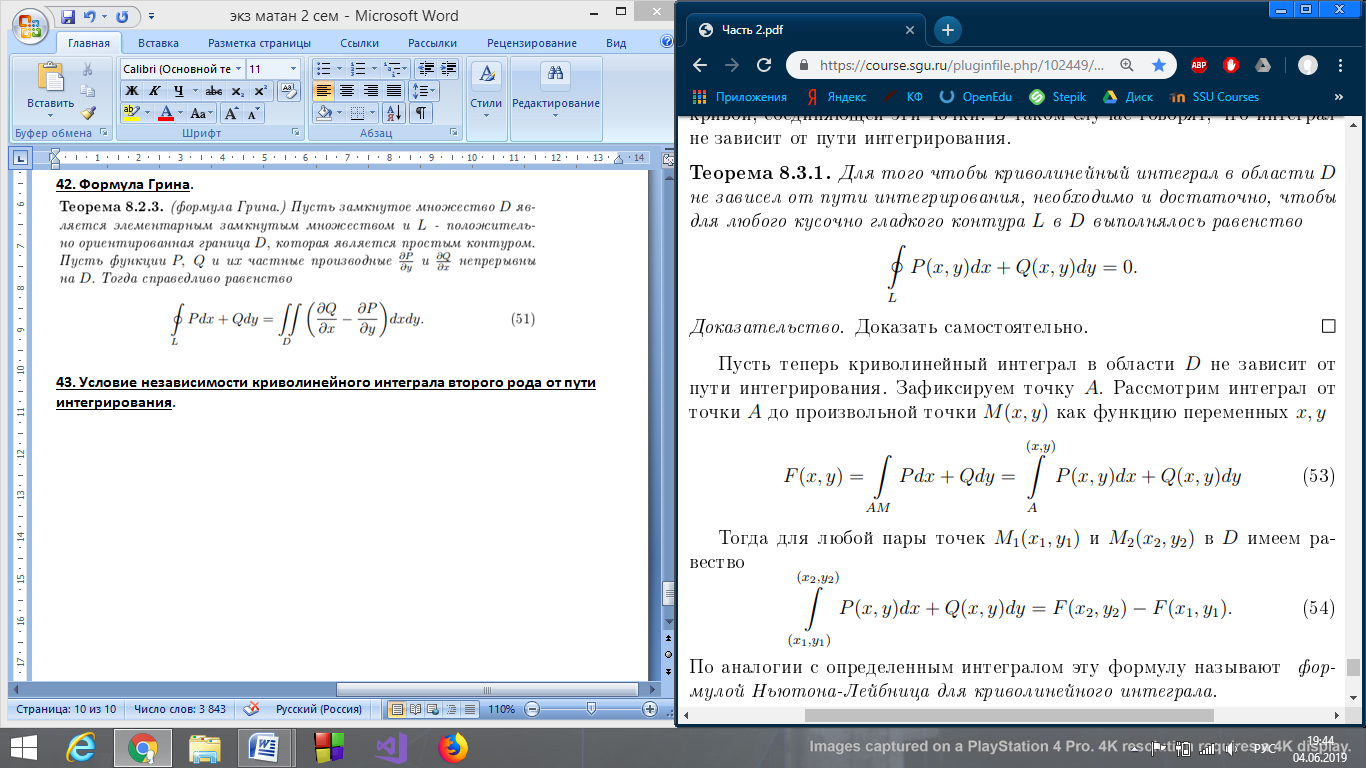
Необходимость:
Пусть
интеграл не зависит от пути интегрирования,
тогда для произвольного замкнутого
контура
![]() имеем
имеем
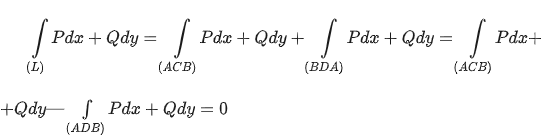
Так как интеграл не зависит от пути интегрирования.
Достаточность:
Докажем, что при выполнении условия теоремы

Для этого докажем, что разность левой и правой частей этого равенства равно нулю:
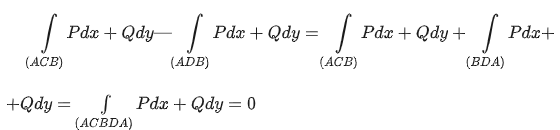
Как интеграл по замкнутому конутру.
