25. Частные производные высшего порядка. Теорема о равенстве смешанных производных. Непрерывно дифференцируемые и k-непрерывно дифференцируемые функции. Дифференциалы первого и высших порядков.

Частная производная второго порядка определяется равенством , где частная производная существует в некоторой окрестности точки и функция имеет в точке частную производную по переменной .Производную также будем обозначать . Если i j, то частную производную называют смешанной. При j = i пишут

Т. о равенстве смешанных производных. Пусть функция f имеет в области G смешанные производные и . Тогда в любой точке , в которой обе частные производные непрерывны, их значения совпадают.

Док-во. Пусть и непрерывны в точке в любой точке . Определим функцию для малого h .

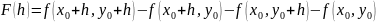Введем функцию

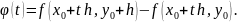
Тогда верно равенство .

По теореме Лагранжа найдется точка такая, что верно равенство .

Пользуясь формулой дифференцирования сложной функции, получим .

Пользуясь теоремой Лагранжа, представим , где ∈ (0, 1).

Имеем равенство .

Если ввести функцию , то . Аналогично придем к равенству , где , ∈ (0, 1).

Следовательно, верно равенство .

Переходя к пределу при h->0 в силу непрерывности обеих частных производных в точке получим .

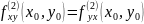Пусть функция f определена в некоторой области G. Назовем функцию n-непрерывно дифференцируемой, если все частные производные до порядка n включительно определены и непрерывны в области G. Класс таких функций обозначается .

Пусть функция f дифференцируема в точке . Функция называется дифференциалом функции f в точке , полагая для любого . Пусть функция f 2-дифференцируемa в точке . Для каждого определим в окрестности O( ) точки функцию полагая для каждого O( )

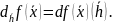
Дифференциалом 2-го порядка функции f в точке называется функция такая, что для :

= .

Пусть функция f n-дифференцируема в точке . Ее n-дифференциалом в этой точке называется функция такая, что для любого .

26. Т. Формула Тейлора с остаточным членом в форме Лагранжа.

Пусть функция f n-дифференцируема в некоторой окрестности О( точки . Тогда при любом ∈ О( справедливо равенство , где .

Док-во.

Рассмотрим функцию одной переменной и воспользуемся для нее формулой Тейлора с остаточным членом в форме Лагранжа. Тогда

Т. формула Тейлора с остаточным членом в форме Пеано. Если функция f n-непрерывно дифференцируема в некоторой окрестности точки , то справедлива формула Тейлора-Пеано .

27. Локальный экстремум функции многих переменных. Необходимое условие локального экстремума. Достаточное условие локального экстремума.

Пусть точка является внутренней точкой области определения функции f. Точка называется точкой локального максимума (минимума) (экстремума), если существует окрестность О( этой точки такая, что f( )<=f( ) (f( )=>f( )).

Т. необходимое условие локального экстремума. Пусть точка является точкой локального экстремума функции f и в этой точке у функции существуют все частные производные первого порядка ), i=1,…,m. Тогда 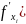при i=1,…,m.

Док-во.

Рассмотрим функцию . Это функция одной переменной имеет в точке локальный экстремум и ее производная . По теореме Ферма . Для i=2,…,m аналогично.

Т. достаточное условие локального экстремума. Пусть функция f определена в некоторой окрестности О( точки , f∈ и точка является критической точкой этой функции. Если квадратичная форма

1) знакоопределена, если положительно определена, то в точке функция имеет локальный экстремум, который является строгим локальным минимумом, и если отрицательно определена, то строгий локальный максимум;

2) неопределенна, то в точке функция экстремума не имеет.

Док-во. По формуле Тейлора с остаточным членом в форме Пеано имеем

Где о(1) есть бесконечно малая функция при → 0. Таким образом, знак разности 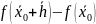определяется знаком величины, стоящей в квадр.скобках.

Вектор имеет единичную норму. Квадратичная форма является непрерывной функцией. Следовательно, на единичной сфере S(0, 1)= { ∈ R^m : | | = 1} являющейся компактом форма принимает как наименьшее (m), так и наибольшее (M) значение.

Если квадратичная форма положительно определена, то 0 < m ≤ M и найдется δ>0 такое, что при | |< δ будет |o(1)| < m. Тогда при | |< δ выражение в квадратных скобках окажется положительным и => . В этом случае точка оказывается точкой строгого локального минимума функции f. Аналогично для локального максимума. 1) доказано.

Если квадратичная форма не является определенной, то m < 0 < M. Пусть и

- те точки единичной сферы, в которых f( ) = m и f( . Полагая, что , где t достаточно мало, имеем где о(1)-> при t->0. При достаточно малом t сумма m+o(1) будет иметь знак числа m, т.к. отрицательный. Тогда отрицательной будет и левая часть равенства. Аналогично для и следовательно, при достаточно малых значениях t разность будет положительна. Значит, что точка не является точкой локального экстремума функции f.

28. Дифференцируемые вектор-функции, матрица Якоби и якобиан.

Вектор-функцию называют дифференцируемой в точке , если все функции дифференцируемы в точке .

Вектор-столбец называется дифференциалом .

Матрица называется матрицей Якоби отображения .

Если n=m, то определитель матрицы Якоби называют якобианом и обозначают .

29. Неявные функции. Теорема о неявной функции.

Пусть даны функция множества X ∈ R^m, Y ∈ R и уравнение . Если для каждого существует единственное число такое, что 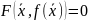, то уравнение на множестве X × Y определяет неявную функцию f: X->Y.

Т. теорема о неявной функции. Если функция F, определенная в окрестности U точки такова, что:

1) F ∈ U) (т.е F непрерывно дифференцируема на U)

2) F = 0

3) 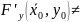0

то найдутся окрестности O(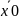 ) и O(y₀) такие, что на множестве O( )×O(y₀) уравнение определяет непрерывно дифференцируемую функцию f : O( ) -> O(y₀) и для любого ∈ O( ) и k = 1, . . . , m верно .

30. Условный экстремум. Необходимое условие условного экстремума и метод множителей Лагранжа.

Условный экстремум – экстремум, аргументы которого удовлетворяют дополнительным условиям связи.

Пусть функции f, g_i(i = 1, . . . , r), являющиеся отображениемя из R^m в R, определены в некоторой окрестности точки и Значение f( называется условным максимумом (минимумом) функции f при условиях связи i = 1, . . . , r, если существует такая окрестность О( , что f( является наибольшим (наименьшим) значением сужения функции на множество .

Т. необходимое условие условного экстремума (теорема Лагранжа). Пусть функции f и g непрерывно дифференцируемы в некоторой окрестности точки и и вектор-градиент grad g( . Если функция f имеет условный экстремум в точке с условием , то существует такое число λ ∈ R, что grad(f- λg)( .

Док-во. Пусть Выберем такое число λ ∈ R, что верно . Докажем это равенство при i = 1, . . . , m – 1.

По теореме о неявной функции существуют такие окрестности , что уравнение определяет неявную дифференцируемую функцию .

В окрестности рассмотрим функцию Из определения условного экстремума следует, что функция F имеет локальный экстремум в точке . По теореме Ферма при любом i = 1, . . . , m−1 имеет равенства .

По теореме о неявной функции при i = 1, . . . , m−1 имеем => .

Метод множителей Лагранжа – метод нахождения условного экстремума.

1) Строят функцию F( , ) = f( )- λg( ).

2) Для нахождения точки возможного условного экстремума решают систему уравнений

3) Для получения достаточного условия экстремума в точке у функции f при наличии связи следует присоединить к системе требование знакоопределенности в этой точке d²F. Минимум если d²F>0 и максимум если d²F<0. В случае нескольких уравнений связи следует построить функцию Лагранжа j = 1,…, n. и далее аналогично.

31. Плоские множества, измеримые по Жордану.

Мн-во F называется измеримым по Жордану (квадрируемым), если верхняя и нижняя его меры равны . Множество точек плоскости назовем множеством меры нуль, если оно содержится в многоугольной фигуре сколь угодно малой меры. Плоская фигура F измерима по Жордану (квадрируема) тогда и только тогда, когда ее граница F имеет меру нуль. Основные свойства площади:

32. Определение двойного интеграла. Критерий интегрируемости и достаточные условия интегрируемости. Основные свойства двойного интеграла.

Пусть D – квадрируемое замкнутое множество. Разбиением T множества D будем называть набор квадрируемых замкнутых множеств D₁, … , D_n с условиями:

Функцию f называют интегрируемой на множестве D, если существует предел I интегральных сумм при диаметре разбиения d(T)->0:

∀e > 0 ∃δ > 0 ∀T ∀{( )} (d(T) < δ ⇒ |σ − I| < e)

Число I называют двойным интегралом от функции f(x,y) по множеству D и обозначается .

Т. Пусть функция f определена и ограничена на квадрируемом множестве D. Функция f интегрируема на D 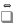верхний интеграл Дарбу равен нижнему интегралу Дарбу.

Т.Критерий интегрируемости. Для того, чтобы ограниченная на квадрируемом множестве D функция f была интегрируема на D, необходимо и достаточно, чтобы ∀e > 0 нашлось такое разбиение Т, что разность верхней и нижней сумм Дарбу была меньше e (S(T) − s(T) < е). Достаточные условия интегрируемости: Всякая непрерывная на квадрируемом множестве функция интегрируема на нем. Пусть функция f определена и ограничена на квадрируемом множестве Dю Если функция f непрерывна на D всюду, кроме точек некоторого множества меры нуль, то она интегрируема на D. Пусть функции f и g определены, ограничены на квадрируемом множестве D и отличаются друг от друга на некотором множестве меры нуль. Тогда интегрируемость одной функции равносильна интегрируемости другой, причем

Основные св-ва двойного интеграла:

1. Аддитивность интеграла. Если и квадрируемые мн-ва не имеет общих внутренних точке, то

2. Линейность интеграла. Пусть f и g интегрируемы на D, α, β ∈ R. Тогда функция αf+βg тоже интегрируема на D и верно .

3. Монотонность интеграла. Пусть f и g интегрируемы на D и f(x, y) ≤ g(x, y), тогда .

4. Пусть f и g интегрируемы на D, тогда fg тоже интегрируема на D.

5. Если функция f интегрируема на D и удовл.условию |f(x, y)| ≥ c >0, (x, y) ∈ D, то функция 1/f тоже интегрируема на D.

6.Если функция f интегрируема на D, то |f| тоже интегрируема на D и верно .

7. .

8. Т.о среднем значении. Если f и g интегрируемы на D, g>0 на D, M = sup_D f(x, y), m = inf _D f(x, y), то найдется число µ ∈ [m, M] такое, что верно .

33. Сведение двойного интеграла к повторному.

Т. Пусть функция f интегрируема в прямоугольнике P = [a, b] × [c, d] и для каждого x ∈ [a, b] существует однократный интеграл .

Тогда существует повторный интеграл и верно .

Док-во.

Разобьем прямоугольник Р на n · p прямоугольников где

Пусть – верхняя и нижняя суммы Дарбу функции f. Тогда всюду на прямоугольнике .

Фиксируем и x= проинтегрируем его по у в пределах от до . Получим .

Умножим все части неравенства на , просуммируем по всем l = 1, . . . , p и k = 1, . . . , n. Будем иметь .

Пусть Тогда . При этом s и S стремятся к двойному интегралу. Следовательно существует предел м среднего члена неравенства, равный тому же двойному интегралу 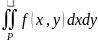. По определению однократного интеграла .

34. Замена переменных в двойном интеграле.

Т. о замене переменных в двойном интеграле. Пусть отображение x=x(u,v), y=y(u, v), (u,v) )∈G* взаимнооднозначно, непрерывно дифференцируемо и отображает область G* на область D*, причем якобиан J(u,v) этого отображение в G* не равен нулю. Если D⊂D∗ квадрируемое замкнутое мн-во и f(x, y) – функция, непрерывная на D или ограничена в D и непрерывна в D всюду, кроме некоторого мн-ва меры нуль, то верна формула , где G является прообразом мн-ва D.

Док-во. Рассмотрим разбиение замкнутой области G на n частичных областей G_i c площадями . Образы областей при отображении образуют разбиение замкнутой области D. В каждой частичной области , площадь которой обозначим через , выберем произвольную точку и составим интегральную сумму , соответствующую двойному интегралу из левой части равенства.

Для каждой из частичных областей имеем Согласно теореме о среднем для двойного интеграла, в области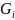 найдется точка , для которой справедливо равенство . Т.к. в интегральной сумме выбор точек произволен, то пусть . Тогда , а это есть интегральная сумма, соответствующая двойному интегралу. Этот интеграл существует в силу условий теоремы. Если диаметр разбиения замкнутой области G устремить к 0, то в силу равномерной непрерывности отображения диаметр разбиения замкнутой области D также будет стремиться к 0. В результате предельного перехода получим .