17. Пространство Rm . Последовательности в Rm и их свойства.

Пусть m ∈ N. Множество упорядоченных наборов (х₁, …, х_m), где x_i ∈ R, i = 1,…,m называют пространством R^m.

Операции в R^m:

1. Сложение = (x₁,…,x_m) и = (y₁,…,y_m) = (x₁ + y₁,…,x_m + y_m)

2. Умножение на скаляр = (x₁,…,x_m) и 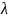∈ R λ = (λx₁,…, λx_m)

3. Отношение равенства = - =

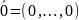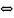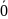
4. Скалярное произведение * = x₁y₁ + … + x_my_m

5. Евклидова норма =

Отображение множества N в множество R^m называют последовательностью и обозначают 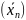, где 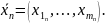Последовательности соответствует m числовых последовательностей, которые называют координатными последовательностями.

Cв-ва последовательностей:

1. Последовательность является ограниченной, бесконечно малой или фундаментальной ⇔ все ее координатные последовательности 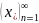i = 1,…, m являются ограниченными, бесконечно малыми или фундаментальными соответственно.

2.

3. Пусть . Тогда +

, ,

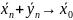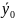
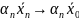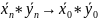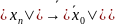
4. Всякая сходящаяся последовательность ограничена.

5. Любая подпоследовательность сходящейся последовательности сходится к той же самой точке.

6. Критерий Коши. Последовательность сходится она фундаментальна.

7. Т.Больцано-Вейерштрасса. У любой ограниченной последовательности существует сходящаяся подпоследовательность.

18. Вектор-функции векторного переменного. Предел и непрерывность функции в точке. Непрерывность функции на множестве. Равномерная непрерывность и теорема Кантора. Теорема о непрерывном образе компакта и ее следствия.

Отображение вида , где Х ⊂ R^m, m > 1, называют функцией многих переменных, а точнее скалярной функцией многих переменных. Отображение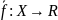 ^k, где Х ⊂ R^m, m > 1, k > 1 называют вектор-функцией векторного аргумента. Вектор-функцию векторного аргумента 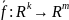можно рассматривать как совокупнос ть k скалярных функций f_i , I = 1,…,k, полагая, что , ∈ D(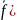 Функции f_i , I = 1,…,k называют координатными функциями вектор-функции .

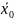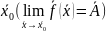Предел по Коши. Пусть точка - предельная точка области определения функции ^k, ∈ R^k. Вектор называют пределом функции в точке , если

∀e > 0 ∃δ > 0 ∀ ∈ D( ) (0 < | − | < δ ⇒ | ( ) − | < e).

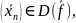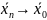Предел по Гейне. Пусть точка - предельная точка области определения функции ^k, ∈ R^k. Вектор называют пределом функции в точке , если для любой последовательности удовлетворяющей условиям: 1) и 2) выполняется ( ) .

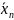Определение предела по Коши равносильно определению предела по Гейне.

Непрерывность по Коши. Функция называется непрерывной в точке , если ∀e > 0 ∃δ > 0 ∀ ∈ D( ) (0 < | − | < δ ⇒ | ( ) − ( ) | < e).

Непрерывность по Гейне. Функция называется непрерывной в точке , если для любой последовательности удовлетворяющей условиям: 1) и 2) выполняется ( ) ( ).

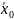Определение непрерывности по Коши равносильно определению непрерывности по Гейне.

Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Т. о непрерывном образе компакта. Пусть функция непрерывна на множестве Х и множество Х – компакт. Тогда множество 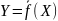тоже компакт.

Следствия:

Т. первая теорема Вейерштрасса. Пусть функция непрерывна на множестве Х и множество Х – компакт. Тогда функция ограничена на Х.

Т. вторая теорема Вейерштрасса. Функция, непрерывная на мн-ве Х, которое является компактом. Тогда функция принимает наименьшее и наибольшее значение на Х.

Функция называется равномерно непрерывной на множестве Х, если

∀е > 0 ∃δ = δ_е > 0 ∀ ∈ X ∀ ’∈ X (| − ’| < δ ⇒ | ( ) − ( ’)| < e).

Т.Кантора. Пусть функция непрерывна на множестве Х и Х – компакт. Тогда функция равномерно непрерывна на Х.